22.3实际问题与二次函数 同步能力提升训练 2021-2022学年人教版九年级数学上册(Word版含答案)
文档属性
| 名称 | 22.3实际问题与二次函数 同步能力提升训练 2021-2022学年人教版九年级数学上册(Word版含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 796.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-03 15:19:14 | ||
图片预览

文档简介
2021-2022学年人教版九年级数学上册《22.3实际问题与二次函数》
同步能力提升训练(附答案)
1.如图,△ABC是直角三角形,∠A=90°,AB=8cm,AC=6cm,点P从点A出发,沿AB方向以2cm/s的速度向点B运动;同时点Q从点A出发,沿AC方向以1cm/s的速度向点C运动,其中一个动点到达终点,则另一个动点也停止运动,则三角形APQ的最大面积是( )
A.8cm2
B.16cm2
C.24cm2
D.32cm2
2.如图,在△ABC中,∠B=90°,AB=6cm,BC=12cm,动点P从点A开始沿边AB向B以1cm/s的速度移动(不与点B重合),动点Q从点B开始沿边BC向C以2cm/s的速度移动(不与点C重合).如果P、Q分别从A、B同时出发,那么经过( )秒,四边形APQC的面积最小.
A.1
B.2
C.3
D.4
3.如图,一边靠墙(墙有足够长),其它三边用12m长的篱笆围成一个矩形(ABCD)花园,这个花园的最大面积是( )
A.16m2
B.12
m2
C.18
m2
D.以上都不对
4.已知二次函数y=x2与一次函数y=2x+1相交于A、B两点,点C是线段AB上一动点,点D是抛物线上一动点,且CD平行于y轴,在移动过程中CD最大值为
.
5.如图,菱形ABCD的边长为8,∠BAD=60°,点E是AD上一动点(不与A、D重合),点F是CD上一动点,且AE+CF=8,则△DEF面积的最大值为
.
6.在边长为2的正方形ABCD中,对角线AC与BD相交于点O,P是BD上一动点,过P作EF∥AC,分别交正方形的两条边于点E,F.设BP=x,△BEF的面积为y,则y与x函数关系式为
.
7.如图,Rt△ABC中,∠ACB=90°,AC=BC=8,D为AB中点,E、F是边AC、BC上的动点,E从A出发向C运动,同时F以相同的速度从C出发向B运动,F运动到B停止,当AE为
时,△ECF的面积最大.
如图1,抛物线y=ax2+bx+c(a≠0)与x轴相交于A、B两点,与y轴交于C(0,3),抛物线的顶点D的坐标为(1,4),点P为第一象限内抛物线上一动点(点P与顶点D不重合).
(1)求抛物线的解析式及A、B两点的坐标;
(2)如图1,过点P作PM⊥x轴于M,交BC于点N,若点N是PM的三等分点,求此时P的坐标;
(3)如图2,当点P在抛物线对称轴的右侧时,过点P作PQ⊥AD于点Q,设抛物线对称轴与x轴交于点H,是否存在这样的点P,以P、D、Q为顶点的三角形与△ADH相似?若存在,求出P点的坐标,若不存在,请说明理由.
9.已知直线y=﹣x+3与x轴相交于点A,与y轴相交于点B.经过A,B两点的抛物线y=ax2+bx+c的对称轴为直线x=1,与x轴的另一个交点为D(D在A的左侧),点P为y轴右侧抛物线上的一动点.
(1)求抛物线的解析式;
(2)若Q为OA的中点,当PQ∥y轴时,求点P的坐标;
(3)当点P位于直线AB上方的抛物线上时,求四边形PADB面积的最大值.
10.如图在平面直角坐标系中放置一直角三角板,其顶点为A'(﹣1,0),B'(0,2),O(0,0),将此三角形绕原点O顺时针旋转90°,得△AOB.
(1)某抛物线经过点A',B,B',求该抛物线的表达式;
(2)点M为第一象限内的抛物线上的一动点,是否存在一点M,使得四边形MB'A'O是平行四边形?若存在,请求出M的坐标,若不存在,说明理由.
(3)求△ABB'的面积.
11.如图,抛物线y=﹣x2+bx+c与x轴交于点A(﹣1,0),B(3,0),与y轴交于点C,点D是直线BC上方抛物线上一动点.
(1)求抛物线的解析式;
(2)如图1,过点D作DE⊥x轴于点E,交直线BC于点M.当DM=2ME时,求点D的坐标;
12.如图,抛物线y=ax2+bx﹣6与x轴相交于A,B两点,与y轴相交于点C,A(﹣2,0),B(4,0),直线l是抛物线的对称轴,在直线l右侧的抛物线上有一动点D,连接AD,BD,BC,CD.
(1)求抛物线的函数表达式:
(2)若点D在x轴的下方,当△BCD的面积是时,求△ABD的面积;
(3)在直线l上有一点P,连接AP,CP,则AP+CP的最小值为
;
(4)在(2)的条件下,点M是x轴上一点,点N是抛物线上一动点,是否存在点N,使得以点B,D,M,N为顶点的四边形是平行四边形,若存在,请直接写出点N的坐标;若不存在,请说明理由.
13.如图,在平面直角坐标系中,抛物线y=x2+2x经过x轴上的A点,直线AB与抛物线在第一象限交于点B(2,6).
(1)求直线AB的函数解析式;
(2)已知点Q是抛物线的对称轴上的一个动点,当△BOQ的周长最小时,求△BOQ的面积;
(3)若以点A,O,B,N为顶点的四边形是平行四边形,则点N的坐标是
.
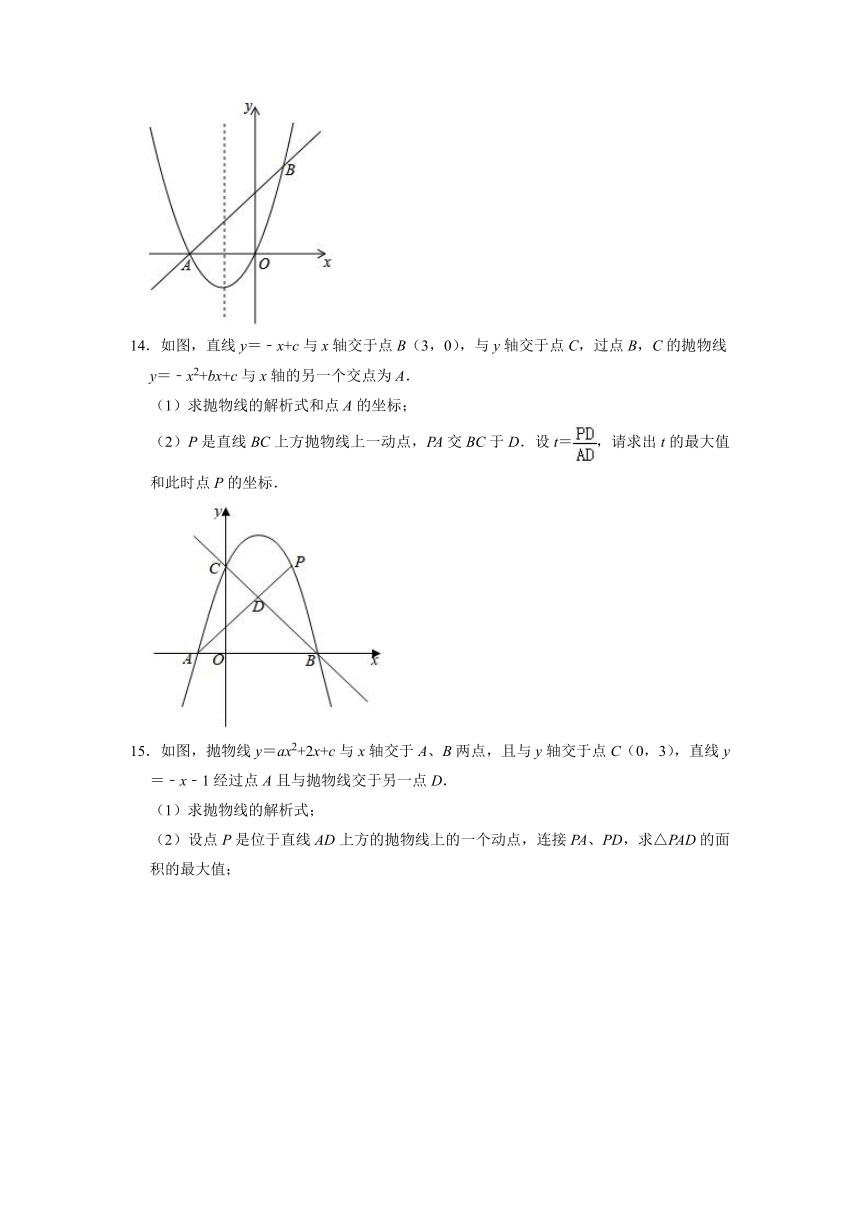
14.如图,直线y=﹣x+c与x轴交于点B(3,0),与y轴交于点C,过点B,C的抛物线y=﹣x2+bx+c与x轴的另一个交点为A.
(1)求抛物线的解析式和点A的坐标;
(2)P是直线BC上方抛物线上一动点,PA交BC于D.设t=,请求出t的最大值和此时点P的坐标.
15.如图,抛物线y=ax2+2x+c与x轴交于A、B两点,且与y轴交于点C(0,3),直线y=﹣x﹣1经过点A且与抛物线交于另一点D.
(1)求抛物线的解析式;
(2)设点P是位于直线AD上方的抛物线上的一个动点,连接PA、PD,求△PAD的面积的最大值;
16.如图,抛物线y=a(x﹣2)2﹣2与y轴交于点A(0,2),顶点为B.
(1)求该抛物线的解析式;
(2)平行于x轴的直线与抛物线交于PQ两点(点Q在点P的右边),若|PQ|=3,求P,Q两点的坐标;
(3)在(2)的条件下,若点C是线段QB上的动点,经过点C的直线y=﹣x+m与y轴交于点D,连接DQ,DB,求△BDQ的面积的最大值和最小值.
17.如图,已知抛物线与x轴交于点A,点B(1,0),与y轴相交于点C(0,﹣2),直线AC经过点A、C.
(1)求抛物线和直线AC的解析式;
(2)若在直线AC上方的抛物线上有一点Q,使△AQC的面积最大,求出△AQC的最大面积并求出此时点Q的坐标;
(3)若点M是抛物线上一动点,过M作MN⊥x轴于点N,是否存在点M,使得以A、M、N为顶点的三角形与△AOC相似?若存在,请求出点M的坐标;若不存在,请说明理由.
18.如图,在平面直角坐标系xOy中,已知抛物线y=ax2+bx+3与x轴交于A(﹣1,0),B(3,0)两点,与y轴交于点D,抛物线顶点为E,C、D两点关于抛物线的对称轴对称,直线y=kx+b恰好经过A、C两点.
(1)求抛物线和直线AC的函数解析式;
(2)设点P是直线AC上方抛物线上的一动点,过点P作y轴的平行线交AC于点H,设点P的横坐标为x.
①用含x的代数式表示线段PH的长;
②当△PAC的面积为时,求点P的坐标.
19.如图1,在直角坐标系中,抛物线C1:y=﹣x2+x+3与x轴交于A、B两点(A在点B的左侧),与y轴交于点C.
(1)求直线BC解析式;
(2)若点P是第一象限内抛物线上一点,过点P作PE∥x轴交BC于点E,求线段PE的最大值及此时的点P的坐标;
(3)点M是直线BC上的动点,点N是抛物线C1上的动点,是否存在以点O、C、M、N为顶点的四边形为平行四边形?若存在,请直接写出点M的坐标;若不存在,请说明理由.
20.一段长为30m的墙MN前有一块矩形ABCD空地,用100m长的篱笆围成如图所示的图形(靠墙的一边不用篱笆,篱笆的厚度忽略不计),其中四边形AEFH和四边形CDHG是矩形,四边形EBGF是边长为10m的正方形,设CD=xm.
(1)若矩形CDHG面积为125m2,求CD长;
(2)当CD长为多少m时,矩形ABCD的面积最大,最大面积是多少?
参考答案
1.解:根据题意
沿AB方向以2cm/s的速度向点B运动;同时点Q从点A出发,沿AC方向以1cm/s的速度向点C运动,
∴AP=2t,AQ=t,
S△APQ=t2,
∵0<t≤4,
∴三角形APQ的最大面积是16.
故选:B.
2.解:设P、Q同时出发后经过的时间为ts,四边形APQC的面积为Scm2,则有:
S=S△ABC﹣S△PBQ
=×12×6﹣(6﹣t)×2t
=t2﹣6t+36
=(t﹣3)2+27.
∴当t=3s时,S取得最小值.
故选:C.
3.解:设与墙垂直的矩形的边长为xm,
则这个花园的面积是:S=x(12﹣2x)=﹣2x2+12x=﹣2(x﹣3)2+18,
∴当x=3时,S取得最大值,此时S=18,
故选:C.
4.解:根据题意得,CD=2x+1﹣x2=﹣x2+2x+1=﹣(x2﹣2x+1﹣1)+1=﹣(x2﹣2x+1)+2=﹣(x﹣1)2+2,
可见CD的最大值为2.
故答案为2.
5.解:过点F作FG⊥AD交AD的延长线于点G,
∵菱形ABCD边长为8,∠BAD=60°,
∴AD=CD=8,∠ADC=180°﹣∠BAD=120°,
∴∠FDG=180°﹣∠ADB=60°,
设AE=x,
∵AE+CF=8,
∴CF=8﹣x;
∴DE=AD﹣AE=8﹣x,DF=CD﹣CF=8﹣(8﹣x)=x,
在Rt△DFG中,FG=x,
∴S△DEF=DE FG=×(8﹣x)×x=﹣x2+2x=﹣(x2﹣8x)=﹣(x﹣4)2+4,
∴当x=4时,△DEF面积的最大,最大值为4.
故答案为:4.
6.解:∵四边形ABCD是正方形,
∴AC=BD=2,OB=OD=BD=,
①当P在OB上时,即0≤x≤,
∵EF∥AC,
∴△BEF∽△BAC,
∴EF:AC=BP:OB,
∴EF=2BP=2x,
∴y=EF BP=×2x×x=x2;
②当P在OD上时,即<x≤2,
∵EF∥AC,
∴△DEF∽△DAC,
∴EF:AC=DP:OD,
即EF:2=(2﹣x):,
∴EF=2(2﹣x),
∴y=EF BP=×2(2﹣x)×x=﹣x2+2x,
综上所述,y=.
故答案为:y=.
7.解:设点E运动的距离为a,则点F运动的距离也为a,
S△ECF==,
∴当a=4时,△ECF的面积最大,
故答案为:4.
8.解:(1)∵抛物线的顶点为D(1,4),
∴设抛物线的解析式为:y=a(x﹣1)2+4,
∵抛物线经过点C(0,3),
∴将C(0,3)代入y=a(x﹣1)2+4,
得:a+4=3,
解得:a=﹣1,
即:y=﹣(x﹣1)2+4,整理得:y=﹣x2+2x+3,
∴抛物线的解析式为:y=﹣x2+2x+3;
(2)令y=0,得:﹣x2+2x+3=0,
解得:x1=﹣1,x2=3,
即:A(﹣1,0),B(3,0),
设直线BC的解析式为:y=kx+b,
将B(3,0),C(0,3)代入得:
,
解得:,
∴直线BC的解析式为:y=﹣x+3,
∵如图1,点P为第一象限内抛物线上一动点,PM⊥x轴于M,交BC于点N,
∴设P(m,﹣m2+2m+3),N(m,﹣m+3),M(m,0),其中0<m<3,
∴PN=﹣m2+3m,NM=﹣m+3,PM=﹣m2+2m+3,
∵点N是PM的三等分点,
∴PN=PM或NM=PM,
①若PN=PM,则﹣m2+3m=(﹣m2+2m+3),
解得:m=或m=3(不合题意,舍去),
将m=代入抛物线解析式得:y=,
∴此时点P的坐标为:P(,);
②若NM=PM,则﹣m+3=(﹣m2+2m+3),
解得:m=2或m=3
(不合题意,舍去),
将m=2代入抛物线解析式得:y=3,
此时点P的坐标为:P(2,3);
综上,点P的坐标为P(,)或P(2,3);
(3)∵抛物线的对称轴为直线x=1,
∴当点P在抛物线对称轴的右侧时,设P(n,﹣n2+2n+3),其中1<n<3,
设直线AD的解析式为y=k1x+b1,
∵A(﹣1,0),D(1,4),
∴,
解得:,
∴直线AD的解析式为y=2x+2,
∵PQ⊥AD,
设直线PQ的解析式为:y=﹣x+d,
将P(n,﹣n2+2n+3),代入y=﹣x+d,
得:d=﹣n2+n+3,
∴直线PQ的解析式为:y=﹣x﹣n2+n+3,
设直线PQ交对称轴于点J,则J(1,﹣n2+n+),
作PK垂直于对称轴于点K,则K(1,﹣n2+2n+3),
∴DJ=n2﹣n+,JK=n﹣,
由题意,可得∠ADH=∠JDQ=∠JPK,
在Rt△ADH中,AH=2,DH=4,
∴AD==2
∴在Rt△DQJ中,
QJ=(n2﹣n+),
DQ=(n2﹣n+),
同理,在Rt△JPK中,PJ=(n﹣),
∴PQ=QJ+PJ=n2﹣,
若以P、D、Q为顶点的三角形与△ADH相似,
∵∠DHA=∠PQD=90°,
∴∠ADH=∠DPQ或∠ADH=∠PDQ,
①若=2,
∴DQ=2PQ,
∴(n2﹣n+)=2(n2﹣),
解得:n=1,
经检验,n=1不是上述分式方程的解.
∴不符合题意,舍去;
②若=,
∴2DQ=PQ,
∴2×(n2﹣n+)=n2﹣,
解得:n=或n=1(不符合题意,舍去),
经检验,n=是上述分式方程的解,
将n=代入抛物线解析式得:y=,
即:点P的坐标为:P(,),
∴当P(,)时,满足以P、D、Q为顶点的三角形与△ADH相似.
9.解:(1)对于y=﹣x+3,令y=0,即0=﹣x+3,解得x=3;令x=0,得y=3;
∴A(3,0),B(0,3),
∵抛物线y=ax +bx+c经过A(3,0),B(0,3)两点,且对称轴为直线x=1,
∴,
解得,
∴抛物线的解析式为:y=﹣x +2x+3;
(2)∵A(3,0),
∴OA=3,
∵Q为OA的中点,
∴OQ=OA=×3=,
∴Q(,0),
∵PQ∥y轴,
∴点P的横坐标为,
当x=时,
y=﹣x +2x+3=﹣+2×+3=,
∴点P的坐标为(,);
(3)过点P作PN∥y轴交直线AB于N,如图:
对于y=﹣x +2x+3,令y=0,即0=﹣x +2x+3,
解得x1=3,x2=﹣1,
∴A(3,0),D(﹣1,0),
∴AD=3﹣(﹣1)=4,
∵B(0,3),
∴OB=3,
∴S△ADB=AD OB=×4×3=6,
设P(m,﹣m +2m+3),则N(m,﹣m+3),
∴PN=﹣m +2m+3﹣(﹣m+3)=﹣m +3m,
∴S△PAB=S△PNB+S△PNA
=PN m+PN (3﹣m)
=PN
=(﹣m +3m),
∴S四边形PADB=S△PAB+S△ABD
=(﹣m +3m)+6
=﹣+,
∵﹣<0,
∴当m=时,S四边形PADB有最大值,最大值为,
∴四边形PADB面积的最大值为.
10.解:(1)由题意得:B(2,0),
设抛物线y=a(x+1) (x﹣2),
∴a 1×(﹣2)=2,
∴a=﹣1,
∴y=﹣(x+1) (x﹣2),
∴y=﹣x2+x+2;
(2)存在,
过点B'作B'M∥A'O交抛物线于M点,
∵B'(0,2),
∴M
(
x,2),
∵点M
(
x,2)在抛物线y=﹣x+x+2上,
∴﹣x2+x+2=2,
∴x1=1,x2=0(舍去),
∴M(1,2)
∴A'O=B'M=1,
又∵B'M∥A'O,
∴四边形MB'A'O是平行四边形,
∴存在M(1,2);
(3)
∵OB'=2,OA=1,
∴AB'=1,
∴
=×1×2
=1.
11.解:(1)∵抛物线y=﹣x2+bx+c与x轴交于点A(﹣1,0),B(3,0),
∴.
解得:.
∴抛物线解析式为y=﹣x2+2x+3.
(2)∵当x=0时,y=﹣x2+2x+3=3,
∴C(0,3).
设直线BC的解析式为y=kx+n,
∴,
解得:.
∴直线BC的解析式为y=﹣x+3.
设D(m,﹣m2+2m+3),则DE=﹣m2+2m+3.
∵DE⊥x轴于点E,
∴M(m,﹣m+3),E(m,0).
∴ME=﹣m+3.
∴DM=DE﹣ME=﹣m2+2m+3﹣(﹣m+3)=﹣m2+3m,
∵DM=2ME,
∴﹣m2+3m=2(﹣m+3).
解得m1=2,m2=3(此时B,D重合,不合题意舍去).
∴m=2.
∴D(2,3).
12.解:(1)把A(﹣2,0)、B(4,0)代入抛物线y=ax2+bx﹣6,
得,解得,
∴抛物线的函数表达式为:.
(2)如图1,过D作DG⊥x轴于G,交BC于H,
抛物线,当x=0时,y=﹣6,
∴C(0,﹣6),
设直线BC的解析式为:y=mx+n,则,
解得,,
∴直线BC的函数表达式为:,
由A(﹣2,0)、B(4,0)关于直线l对称,得直线l为x=1,
设D(x,)(1<x<4),则H(x,),
∴,
∵△BCD的面积是,
∴DH×OG+DH×BG=,
∴,
整理得,x2﹣4x+3=0,
解得:x=3或x=1(不符合题意,舍去),
∴,
∴DG=,
∵AB=4﹣(﹣2)=6,
∴S△ABD=;
(3)如图2,设BC交直线l于点P′,连结P′A、PB,
∵直线l是抛物线的对称轴,
∴直线l是线段AB的垂直平分线,
∴AP′=BP′,AP=BP,
∴AP′+CP′=BP′+CP′=BC,AP+CP=BP+CP,
∵BP+CP≥BC,
∴AP+CP≥AP′+CP′,
∴当点P与点P′重合,即点P在线段BC上时,AP+CP=BC,此时AP+CP的值最小,
∵∠BOC=90°,OB=4,OC=6,
∴BC===,
∴AP+CP的最小值为.
(4)存在.
如图1,点N在x轴的下方,作DG⊥x轴于点G,
将△DBG沿x轴向左平移,使点N落在抛物线上,得到△NML,
则四边形BDNM是平行四边形;
连结BN,作DM′∥BN交x轴于点M′,则四边形BNDM′是平行四边形,
∵DN∥BM,
∴DN∥x轴,
∴点N、点D到x轴的距离相等,
∴点N的纵坐标为,
当y=时,由=,整理得,x2﹣2x﹣3=0,
解得,x1=﹣1,x2=3,
∴N;
如图4,点N在x轴的上方,将△BDG绕点B旋转180°后再平移,可得平行四边形BDMN和平行四边形BDM′N′,
作NL⊥x轴于点L,则∠NLM=∠DGB=90°,
∵MN∥BD,
∴∠NML=∠DBG,
∵MN=BD,
∴△MNL≌△BDG(AAS),
∴NL=DG=,
∴点N的纵坐标为,
当y=时,由=,整理得,x2﹣2x﹣13=0,
解得,x1=1,x2=,
∴N或N,
综上所述,点N的坐标为或或.
13.解:(1)在y=x2+2x中,令y=0,得x2+2x=0,
解得:x1=0,x2=﹣4,
∴A(﹣4,0),
设直线AB的解析式为y=kx+b,
∵A(﹣4,0),B(2,6),
∴,
解得:,
∴直线AB的函数解析式为:y=x+4;
(2)如图1,∵y=x2+2x=(x+2)2﹣2,
∴该抛物线对称轴为直线x=﹣2,
∴直线x=﹣2与直线AB交于点Q,
∵点A(﹣4,0)与点O(0,0)关于直线x=﹣2对称,
∴BQ+QO+OB=BQ+QA+OB=AB+OB,此时,△OBQ的周长最小,
∵AB==6,OB==2,
∴△OBQ的周长取最小2时,点Q(﹣2,2),
此时,S△BOQ=S△ABO﹣S△AQO=OA yB﹣OA yQ=OA (yB﹣yQ)=×4×(6﹣2)=8.
(3)点A、O、B、N为顶点的四边形是平行四边形时,设N(m,n),分三种情况:
①以AN、BO为对角线,此时AN中点与CO中点重合,如图2,
∵A(﹣4,0)、O(0,0),B(2,6),
∴AN的中点为(,),OC中点为(,),
∴,
解得:,
∴N(6,6),
②以AB、NO为对角线,此时AB中点与NO中点重合,如图3,
同理可得:,
解得:,
∴N(﹣2,6),
③以AO、BN为对角线,此时AO中点与BN中点重合,如图4,
同理可得:,
解得:,
∴N(﹣6,﹣6),
综上所述,点A、O、C、N为顶点的四边形是平行四边形,
点N的坐标为:(6,6)或(﹣2,6)或(﹣6,﹣6).
故答案为:(6,6)或(﹣2,6)或(﹣6,﹣6).
14.解:(1)∵直线y=﹣x+c与x轴交于点B(3,0),与y轴交于点C,
∴﹣3+c=0,
解得c=3,
∴C(0,3),
∵抛物线经过B,C,
∴,
解得,
∴抛物线的解析式为y=﹣x2+2x+3,
令y=0,得到﹣x2+2x+3=0,解得x=﹣1或3,
∴A(﹣1,0).
(2)法一:如图,过点P作PG∥x轴交直线BC于点G,设P(m,﹣m2+2m+3).
∵PG∥x轴,
∵P是直线BC上方抛物线上一动点,
∴0<m<3,
由直线BC:y=﹣x+3知,G点坐标为(m2﹣2m,﹣m2+2m+3),
故PG=m﹣(m2﹣2m)=﹣m2+3m,
∵AB=4,PG=﹣m2+3m,
∴,
∵,
∴时,t有最大值,最大值为,此时,.
法二:如图2,连接AC,PC,PB,过点A作AE⊥BC于E,过点P作PF⊥BC于F.设P(m,﹣m2+2m+3).
∵AE∥PF,
∵,,
∴,
∵,
∵S△PBC=S△PCO+S△PBO﹣S△BOC==,
∴,
∵,
∴时,t有最大值,最大值为,此时,.
15.解:(1)∵直线y=﹣x﹣1经过点A,
∴令y=0,则0=﹣x﹣1,
∴x=﹣1,
∴A(﹣1,0),
将A(﹣1,0),C(0,3)代入y=ax2+2x+c得
,
解得,
∴抛物线的解析式为:y=﹣x2+2x+3;
(2)如图,过点P作PE⊥x轴,交x轴于点G,交AD于点F,作DE⊥PF于E,
由题意得,
,
解得:x1=﹣1,x2=4,
当x=4时,y=﹣5,
∴D(4,﹣5),
设P(m,﹣m2+2m+3),F(m,﹣m﹣1),
∴PF=﹣m2+2+3﹣(﹣m﹣1)=﹣m2+3m+4,
∴S△PAD=S△PAF+S△PDF=PF AG+PF DE=PF(AG+DE),
∵AG+DE=|xD﹣xA|=5,
∴S△PAD=PF,
∴当PF取最大值时,S△PAD的值最大,
PF=﹣m2+3m+4=﹣(m﹣)2+,
∴PF最大值为,
则△PAD的面积的最大值为=.
16.解:(1)把A(0,2)代入y=a(x﹣2)2﹣2,得a=1.
∴抛物线的解析式为y=(x﹣2)2﹣2=x2﹣4x+2.
(2)由(1)知,抛物线的对称轴为x=2,
设,依题意,
知,
解得.
把代入抛物线,得,
所以P,Q的坐标是.
(3)由(1)知B(2,﹣2),
当直线y=﹣x+m经过点B时,得m=0,
当直线y=﹣x+m经过点Q时,得,
所以m的取值范围是:.
设直线BQ的解析式为:y=kx+b,将B,Q的坐标代入,
得,所以直线BQ的解析式为:.
设直线BQ交y轴于点E,则E(0,﹣5),,
∴.
当m=0时,S△BDQ最小值为,
当时,S△BDQ最大值为.
17.解:(1)将B(1,0)、C(0,﹣2)代入中得:,
∴,
∴该抛物线的对称轴为,
∵B(1,0),
∴A(4,0),
令直线AC的解析式为y=kx+b,将A(4,0),C(0,﹣2),
代入得:,
∴,
(2)令,连接OQ,
则,,
∴,
∵=﹣m2+4m=﹣(m﹣2)2+4,
∵﹣1<0,
∴m=2时,△AQC的面积最大为4,
此时Q(2,1),
(3)存在点M使以A,M,N为顶点的三角形与△OAC相似,
设,则N(a,0),分两种情况,
①若△NMA∽△OAC,则,
即,
则|16﹣4a|=|a2﹣5a+4|,
当a2﹣5a+4=16﹣4a时,得a1=4(舍),a2=﹣3,
当a2﹣5a+4=4a﹣16时,a1=5,a2=4(舍),
即M1(﹣3,﹣14),M2(5,﹣2),
②若△NAM∽△OAC,则,
即,
则|2a2﹣10a+8|=|8﹣2a|,
当2a2﹣10a+8=8﹣2a时,a1=0,a2=4(舍),即M3(0,﹣2),
当2a2﹣10a+8=2a﹣8时,a1=2,a2=4(舍),即M4(2,1),
综上所述,M1(﹣3,﹣14),M2(5,﹣2),M3(0,﹣2),M4(2,1).
18.(1)把A(﹣1,0),B(3,0)两点分别代数入y=ax2+bx+3得:
a﹣b+3=0,9a+3b+3=0,
解得:a=﹣1,b=2,
∴抛物线解析式为:y=﹣x2+2x+3,
∴点D的坐标为(0,3),
抛物线的对称轴为直线x=1,顶点E(1,4),
∵C、D两点关于抛物线的对称轴对称,
∴点C(2,3),
将点A、C的坐标代入一次函数表达式得:,
解得,
∴直线AC的表达式为y=x+1,
(2)①∵点P的横坐标为x.则点P,H的坐标分别为
P(x,﹣x2+2x+3),H(x,x+1),
∴PH=﹣x2+2x+3﹣x﹣1=﹣x2+x+2;
②∵△PAC的面积=S△PHA+S△PHC=(xC﹣xA)
=,
∴﹣x2+x+2=,
解得:x=或x=(不合题意,舍去),
当x=时,y=﹣x2+2x+3=,
∴P点的坐标为(,).
19.解:(1)∵抛物线C1:y=﹣x2+x+3与x轴交于A、B两点,
∴当y=0时,﹣x2+x+3=0,解得x1=4,x2=﹣,
∴A(﹣,0),B(4,0),
当x=0时,y=3,
∴C(0,3),
设直线BC的函数解析式为:y=kx+b,
,
解得,
∴直线BC的函数解析式为:y=﹣x+3;
(2)设点P(m,﹣),
∵PE∥x轴,
∴点E的纵坐标为﹣,
∵点E在直线BC上,
∴点E的横坐标为,
∴PE=m﹣()=﹣,
当m=﹣=2时,PE最大值为﹣=,
此时点P(2,);
(3)当OC为边时,如图,则MN∥OC,MN=OC=3,
设M(t,﹣t+3),则N(t,﹣t2+
),
∴|﹣t+3﹣(﹣t2+
)|=3,
∴||=3,
∴或.
解得t1=2+,t2=2﹣,
∴点M(2+,)或(2﹣,),
当OC为对角线时,
设M(t,﹣t+3),由M点平移到点C,点O平移到点N可知:N(﹣t,
),
∴﹣t2﹣t+3=+1,
∴t2+4t﹣4=0,
解得t=﹣2±2,
∴点M(﹣2+2,)或(﹣2﹣2,),
综上所述:点M(2+,)或(2﹣,)或(﹣2+2,)或(﹣2﹣2,).
20.解:(1)由题意得:3x+20+GC=100,
解得:GC=(80﹣3x)m,
∵BC=BG+GC=10+80﹣3x,
而0<BC≤30,即0<10+80﹣3x≤30,解得20≤x<30,
矩形CDHG面积=GC CD=(80﹣3x)x=125,解得x=25或(舍去),
∴CD长为25m;
(2)设矩形ABCD的面积为s,则s=BC CD=x(10+80﹣3x)=﹣3x2+90x=﹣3(x﹣15)2+675,
∵﹣3<0,故抛物线开口向下,
而20≤x<30,
当x>15时,s随x的增大而减小,
故当x=20(m)时,s取得最大值为﹣3×(20﹣15)2+675=600(m2).
答:当CD长为20m时,矩形ABCD的面积最大,最大面积是600m2.
同步能力提升训练(附答案)
1.如图,△ABC是直角三角形,∠A=90°,AB=8cm,AC=6cm,点P从点A出发,沿AB方向以2cm/s的速度向点B运动;同时点Q从点A出发,沿AC方向以1cm/s的速度向点C运动,其中一个动点到达终点,则另一个动点也停止运动,则三角形APQ的最大面积是( )
A.8cm2
B.16cm2
C.24cm2
D.32cm2
2.如图,在△ABC中,∠B=90°,AB=6cm,BC=12cm,动点P从点A开始沿边AB向B以1cm/s的速度移动(不与点B重合),动点Q从点B开始沿边BC向C以2cm/s的速度移动(不与点C重合).如果P、Q分别从A、B同时出发,那么经过( )秒,四边形APQC的面积最小.
A.1
B.2
C.3
D.4
3.如图,一边靠墙(墙有足够长),其它三边用12m长的篱笆围成一个矩形(ABCD)花园,这个花园的最大面积是( )
A.16m2
B.12
m2
C.18
m2
D.以上都不对
4.已知二次函数y=x2与一次函数y=2x+1相交于A、B两点,点C是线段AB上一动点,点D是抛物线上一动点,且CD平行于y轴,在移动过程中CD最大值为
.
5.如图,菱形ABCD的边长为8,∠BAD=60°,点E是AD上一动点(不与A、D重合),点F是CD上一动点,且AE+CF=8,则△DEF面积的最大值为
.
6.在边长为2的正方形ABCD中,对角线AC与BD相交于点O,P是BD上一动点,过P作EF∥AC,分别交正方形的两条边于点E,F.设BP=x,△BEF的面积为y,则y与x函数关系式为
.
7.如图,Rt△ABC中,∠ACB=90°,AC=BC=8,D为AB中点,E、F是边AC、BC上的动点,E从A出发向C运动,同时F以相同的速度从C出发向B运动,F运动到B停止,当AE为
时,△ECF的面积最大.
如图1,抛物线y=ax2+bx+c(a≠0)与x轴相交于A、B两点,与y轴交于C(0,3),抛物线的顶点D的坐标为(1,4),点P为第一象限内抛物线上一动点(点P与顶点D不重合).
(1)求抛物线的解析式及A、B两点的坐标;
(2)如图1,过点P作PM⊥x轴于M,交BC于点N,若点N是PM的三等分点,求此时P的坐标;
(3)如图2,当点P在抛物线对称轴的右侧时,过点P作PQ⊥AD于点Q,设抛物线对称轴与x轴交于点H,是否存在这样的点P,以P、D、Q为顶点的三角形与△ADH相似?若存在,求出P点的坐标,若不存在,请说明理由.
9.已知直线y=﹣x+3与x轴相交于点A,与y轴相交于点B.经过A,B两点的抛物线y=ax2+bx+c的对称轴为直线x=1,与x轴的另一个交点为D(D在A的左侧),点P为y轴右侧抛物线上的一动点.
(1)求抛物线的解析式;
(2)若Q为OA的中点,当PQ∥y轴时,求点P的坐标;
(3)当点P位于直线AB上方的抛物线上时,求四边形PADB面积的最大值.
10.如图在平面直角坐标系中放置一直角三角板,其顶点为A'(﹣1,0),B'(0,2),O(0,0),将此三角形绕原点O顺时针旋转90°,得△AOB.
(1)某抛物线经过点A',B,B',求该抛物线的表达式;
(2)点M为第一象限内的抛物线上的一动点,是否存在一点M,使得四边形MB'A'O是平行四边形?若存在,请求出M的坐标,若不存在,说明理由.
(3)求△ABB'的面积.
11.如图,抛物线y=﹣x2+bx+c与x轴交于点A(﹣1,0),B(3,0),与y轴交于点C,点D是直线BC上方抛物线上一动点.
(1)求抛物线的解析式;
(2)如图1,过点D作DE⊥x轴于点E,交直线BC于点M.当DM=2ME时,求点D的坐标;
12.如图,抛物线y=ax2+bx﹣6与x轴相交于A,B两点,与y轴相交于点C,A(﹣2,0),B(4,0),直线l是抛物线的对称轴,在直线l右侧的抛物线上有一动点D,连接AD,BD,BC,CD.
(1)求抛物线的函数表达式:
(2)若点D在x轴的下方,当△BCD的面积是时,求△ABD的面积;
(3)在直线l上有一点P,连接AP,CP,则AP+CP的最小值为
;
(4)在(2)的条件下,点M是x轴上一点,点N是抛物线上一动点,是否存在点N,使得以点B,D,M,N为顶点的四边形是平行四边形,若存在,请直接写出点N的坐标;若不存在,请说明理由.
13.如图,在平面直角坐标系中,抛物线y=x2+2x经过x轴上的A点,直线AB与抛物线在第一象限交于点B(2,6).
(1)求直线AB的函数解析式;
(2)已知点Q是抛物线的对称轴上的一个动点,当△BOQ的周长最小时,求△BOQ的面积;
(3)若以点A,O,B,N为顶点的四边形是平行四边形,则点N的坐标是
.
14.如图,直线y=﹣x+c与x轴交于点B(3,0),与y轴交于点C,过点B,C的抛物线y=﹣x2+bx+c与x轴的另一个交点为A.
(1)求抛物线的解析式和点A的坐标;
(2)P是直线BC上方抛物线上一动点,PA交BC于D.设t=,请求出t的最大值和此时点P的坐标.
15.如图,抛物线y=ax2+2x+c与x轴交于A、B两点,且与y轴交于点C(0,3),直线y=﹣x﹣1经过点A且与抛物线交于另一点D.
(1)求抛物线的解析式;
(2)设点P是位于直线AD上方的抛物线上的一个动点,连接PA、PD,求△PAD的面积的最大值;
16.如图,抛物线y=a(x﹣2)2﹣2与y轴交于点A(0,2),顶点为B.
(1)求该抛物线的解析式;
(2)平行于x轴的直线与抛物线交于PQ两点(点Q在点P的右边),若|PQ|=3,求P,Q两点的坐标;
(3)在(2)的条件下,若点C是线段QB上的动点,经过点C的直线y=﹣x+m与y轴交于点D,连接DQ,DB,求△BDQ的面积的最大值和最小值.
17.如图,已知抛物线与x轴交于点A,点B(1,0),与y轴相交于点C(0,﹣2),直线AC经过点A、C.
(1)求抛物线和直线AC的解析式;
(2)若在直线AC上方的抛物线上有一点Q,使△AQC的面积最大,求出△AQC的最大面积并求出此时点Q的坐标;
(3)若点M是抛物线上一动点,过M作MN⊥x轴于点N,是否存在点M,使得以A、M、N为顶点的三角形与△AOC相似?若存在,请求出点M的坐标;若不存在,请说明理由.
18.如图,在平面直角坐标系xOy中,已知抛物线y=ax2+bx+3与x轴交于A(﹣1,0),B(3,0)两点,与y轴交于点D,抛物线顶点为E,C、D两点关于抛物线的对称轴对称,直线y=kx+b恰好经过A、C两点.
(1)求抛物线和直线AC的函数解析式;
(2)设点P是直线AC上方抛物线上的一动点,过点P作y轴的平行线交AC于点H,设点P的横坐标为x.
①用含x的代数式表示线段PH的长;
②当△PAC的面积为时,求点P的坐标.
19.如图1,在直角坐标系中,抛物线C1:y=﹣x2+x+3与x轴交于A、B两点(A在点B的左侧),与y轴交于点C.
(1)求直线BC解析式;
(2)若点P是第一象限内抛物线上一点,过点P作PE∥x轴交BC于点E,求线段PE的最大值及此时的点P的坐标;
(3)点M是直线BC上的动点,点N是抛物线C1上的动点,是否存在以点O、C、M、N为顶点的四边形为平行四边形?若存在,请直接写出点M的坐标;若不存在,请说明理由.
20.一段长为30m的墙MN前有一块矩形ABCD空地,用100m长的篱笆围成如图所示的图形(靠墙的一边不用篱笆,篱笆的厚度忽略不计),其中四边形AEFH和四边形CDHG是矩形,四边形EBGF是边长为10m的正方形,设CD=xm.
(1)若矩形CDHG面积为125m2,求CD长;
(2)当CD长为多少m时,矩形ABCD的面积最大,最大面积是多少?
参考答案
1.解:根据题意
沿AB方向以2cm/s的速度向点B运动;同时点Q从点A出发,沿AC方向以1cm/s的速度向点C运动,
∴AP=2t,AQ=t,
S△APQ=t2,
∵0<t≤4,
∴三角形APQ的最大面积是16.
故选:B.
2.解:设P、Q同时出发后经过的时间为ts,四边形APQC的面积为Scm2,则有:
S=S△ABC﹣S△PBQ
=×12×6﹣(6﹣t)×2t
=t2﹣6t+36
=(t﹣3)2+27.
∴当t=3s时,S取得最小值.
故选:C.
3.解:设与墙垂直的矩形的边长为xm,
则这个花园的面积是:S=x(12﹣2x)=﹣2x2+12x=﹣2(x﹣3)2+18,
∴当x=3时,S取得最大值,此时S=18,
故选:C.
4.解:根据题意得,CD=2x+1﹣x2=﹣x2+2x+1=﹣(x2﹣2x+1﹣1)+1=﹣(x2﹣2x+1)+2=﹣(x﹣1)2+2,
可见CD的最大值为2.
故答案为2.
5.解:过点F作FG⊥AD交AD的延长线于点G,
∵菱形ABCD边长为8,∠BAD=60°,
∴AD=CD=8,∠ADC=180°﹣∠BAD=120°,
∴∠FDG=180°﹣∠ADB=60°,
设AE=x,
∵AE+CF=8,
∴CF=8﹣x;
∴DE=AD﹣AE=8﹣x,DF=CD﹣CF=8﹣(8﹣x)=x,
在Rt△DFG中,FG=x,
∴S△DEF=DE FG=×(8﹣x)×x=﹣x2+2x=﹣(x2﹣8x)=﹣(x﹣4)2+4,
∴当x=4时,△DEF面积的最大,最大值为4.
故答案为:4.
6.解:∵四边形ABCD是正方形,
∴AC=BD=2,OB=OD=BD=,
①当P在OB上时,即0≤x≤,
∵EF∥AC,
∴△BEF∽△BAC,
∴EF:AC=BP:OB,
∴EF=2BP=2x,
∴y=EF BP=×2x×x=x2;
②当P在OD上时,即<x≤2,
∵EF∥AC,
∴△DEF∽△DAC,
∴EF:AC=DP:OD,
即EF:2=(2﹣x):,
∴EF=2(2﹣x),
∴y=EF BP=×2(2﹣x)×x=﹣x2+2x,
综上所述,y=.
故答案为:y=.
7.解:设点E运动的距离为a,则点F运动的距离也为a,
S△ECF==,
∴当a=4时,△ECF的面积最大,
故答案为:4.
8.解:(1)∵抛物线的顶点为D(1,4),
∴设抛物线的解析式为:y=a(x﹣1)2+4,
∵抛物线经过点C(0,3),
∴将C(0,3)代入y=a(x﹣1)2+4,
得:a+4=3,
解得:a=﹣1,
即:y=﹣(x﹣1)2+4,整理得:y=﹣x2+2x+3,
∴抛物线的解析式为:y=﹣x2+2x+3;
(2)令y=0,得:﹣x2+2x+3=0,
解得:x1=﹣1,x2=3,
即:A(﹣1,0),B(3,0),
设直线BC的解析式为:y=kx+b,
将B(3,0),C(0,3)代入得:
,
解得:,
∴直线BC的解析式为:y=﹣x+3,
∵如图1,点P为第一象限内抛物线上一动点,PM⊥x轴于M,交BC于点N,
∴设P(m,﹣m2+2m+3),N(m,﹣m+3),M(m,0),其中0<m<3,
∴PN=﹣m2+3m,NM=﹣m+3,PM=﹣m2+2m+3,
∵点N是PM的三等分点,
∴PN=PM或NM=PM,
①若PN=PM,则﹣m2+3m=(﹣m2+2m+3),
解得:m=或m=3(不合题意,舍去),
将m=代入抛物线解析式得:y=,
∴此时点P的坐标为:P(,);
②若NM=PM,则﹣m+3=(﹣m2+2m+3),
解得:m=2或m=3
(不合题意,舍去),
将m=2代入抛物线解析式得:y=3,
此时点P的坐标为:P(2,3);
综上,点P的坐标为P(,)或P(2,3);
(3)∵抛物线的对称轴为直线x=1,
∴当点P在抛物线对称轴的右侧时,设P(n,﹣n2+2n+3),其中1<n<3,
设直线AD的解析式为y=k1x+b1,
∵A(﹣1,0),D(1,4),
∴,
解得:,
∴直线AD的解析式为y=2x+2,
∵PQ⊥AD,
设直线PQ的解析式为:y=﹣x+d,
将P(n,﹣n2+2n+3),代入y=﹣x+d,
得:d=﹣n2+n+3,
∴直线PQ的解析式为:y=﹣x﹣n2+n+3,
设直线PQ交对称轴于点J,则J(1,﹣n2+n+),
作PK垂直于对称轴于点K,则K(1,﹣n2+2n+3),
∴DJ=n2﹣n+,JK=n﹣,
由题意,可得∠ADH=∠JDQ=∠JPK,
在Rt△ADH中,AH=2,DH=4,
∴AD==2
∴在Rt△DQJ中,
QJ=(n2﹣n+),
DQ=(n2﹣n+),
同理,在Rt△JPK中,PJ=(n﹣),
∴PQ=QJ+PJ=n2﹣,
若以P、D、Q为顶点的三角形与△ADH相似,
∵∠DHA=∠PQD=90°,
∴∠ADH=∠DPQ或∠ADH=∠PDQ,
①若=2,
∴DQ=2PQ,
∴(n2﹣n+)=2(n2﹣),
解得:n=1,
经检验,n=1不是上述分式方程的解.
∴不符合题意,舍去;
②若=,
∴2DQ=PQ,
∴2×(n2﹣n+)=n2﹣,
解得:n=或n=1(不符合题意,舍去),
经检验,n=是上述分式方程的解,
将n=代入抛物线解析式得:y=,
即:点P的坐标为:P(,),
∴当P(,)时,满足以P、D、Q为顶点的三角形与△ADH相似.
9.解:(1)对于y=﹣x+3,令y=0,即0=﹣x+3,解得x=3;令x=0,得y=3;
∴A(3,0),B(0,3),
∵抛物线y=ax +bx+c经过A(3,0),B(0,3)两点,且对称轴为直线x=1,
∴,
解得,
∴抛物线的解析式为:y=﹣x +2x+3;
(2)∵A(3,0),
∴OA=3,
∵Q为OA的中点,
∴OQ=OA=×3=,
∴Q(,0),
∵PQ∥y轴,
∴点P的横坐标为,
当x=时,
y=﹣x +2x+3=﹣+2×+3=,
∴点P的坐标为(,);
(3)过点P作PN∥y轴交直线AB于N,如图:
对于y=﹣x +2x+3,令y=0,即0=﹣x +2x+3,
解得x1=3,x2=﹣1,
∴A(3,0),D(﹣1,0),
∴AD=3﹣(﹣1)=4,
∵B(0,3),
∴OB=3,
∴S△ADB=AD OB=×4×3=6,
设P(m,﹣m +2m+3),则N(m,﹣m+3),
∴PN=﹣m +2m+3﹣(﹣m+3)=﹣m +3m,
∴S△PAB=S△PNB+S△PNA
=PN m+PN (3﹣m)
=PN
=(﹣m +3m),
∴S四边形PADB=S△PAB+S△ABD
=(﹣m +3m)+6
=﹣+,
∵﹣<0,
∴当m=时,S四边形PADB有最大值,最大值为,
∴四边形PADB面积的最大值为.
10.解:(1)由题意得:B(2,0),
设抛物线y=a(x+1) (x﹣2),
∴a 1×(﹣2)=2,
∴a=﹣1,
∴y=﹣(x+1) (x﹣2),
∴y=﹣x2+x+2;
(2)存在,
过点B'作B'M∥A'O交抛物线于M点,
∵B'(0,2),
∴M
(
x,2),
∵点M
(
x,2)在抛物线y=﹣x+x+2上,
∴﹣x2+x+2=2,
∴x1=1,x2=0(舍去),
∴M(1,2)
∴A'O=B'M=1,
又∵B'M∥A'O,
∴四边形MB'A'O是平行四边形,
∴存在M(1,2);
(3)
∵OB'=2,OA=1,
∴AB'=1,
∴
=×1×2
=1.
11.解:(1)∵抛物线y=﹣x2+bx+c与x轴交于点A(﹣1,0),B(3,0),
∴.
解得:.
∴抛物线解析式为y=﹣x2+2x+3.
(2)∵当x=0时,y=﹣x2+2x+3=3,
∴C(0,3).
设直线BC的解析式为y=kx+n,
∴,
解得:.
∴直线BC的解析式为y=﹣x+3.
设D(m,﹣m2+2m+3),则DE=﹣m2+2m+3.
∵DE⊥x轴于点E,
∴M(m,﹣m+3),E(m,0).
∴ME=﹣m+3.
∴DM=DE﹣ME=﹣m2+2m+3﹣(﹣m+3)=﹣m2+3m,
∵DM=2ME,
∴﹣m2+3m=2(﹣m+3).
解得m1=2,m2=3(此时B,D重合,不合题意舍去).
∴m=2.
∴D(2,3).
12.解:(1)把A(﹣2,0)、B(4,0)代入抛物线y=ax2+bx﹣6,
得,解得,
∴抛物线的函数表达式为:.
(2)如图1,过D作DG⊥x轴于G,交BC于H,
抛物线,当x=0时,y=﹣6,
∴C(0,﹣6),
设直线BC的解析式为:y=mx+n,则,
解得,,
∴直线BC的函数表达式为:,
由A(﹣2,0)、B(4,0)关于直线l对称,得直线l为x=1,
设D(x,)(1<x<4),则H(x,),
∴,
∵△BCD的面积是,
∴DH×OG+DH×BG=,
∴,
整理得,x2﹣4x+3=0,
解得:x=3或x=1(不符合题意,舍去),
∴,
∴DG=,
∵AB=4﹣(﹣2)=6,
∴S△ABD=;
(3)如图2,设BC交直线l于点P′,连结P′A、PB,
∵直线l是抛物线的对称轴,
∴直线l是线段AB的垂直平分线,
∴AP′=BP′,AP=BP,
∴AP′+CP′=BP′+CP′=BC,AP+CP=BP+CP,
∵BP+CP≥BC,
∴AP+CP≥AP′+CP′,
∴当点P与点P′重合,即点P在线段BC上时,AP+CP=BC,此时AP+CP的值最小,
∵∠BOC=90°,OB=4,OC=6,
∴BC===,
∴AP+CP的最小值为.
(4)存在.
如图1,点N在x轴的下方,作DG⊥x轴于点G,
将△DBG沿x轴向左平移,使点N落在抛物线上,得到△NML,
则四边形BDNM是平行四边形;
连结BN,作DM′∥BN交x轴于点M′,则四边形BNDM′是平行四边形,
∵DN∥BM,
∴DN∥x轴,
∴点N、点D到x轴的距离相等,
∴点N的纵坐标为,
当y=时,由=,整理得,x2﹣2x﹣3=0,
解得,x1=﹣1,x2=3,
∴N;
如图4,点N在x轴的上方,将△BDG绕点B旋转180°后再平移,可得平行四边形BDMN和平行四边形BDM′N′,
作NL⊥x轴于点L,则∠NLM=∠DGB=90°,
∵MN∥BD,
∴∠NML=∠DBG,
∵MN=BD,
∴△MNL≌△BDG(AAS),
∴NL=DG=,
∴点N的纵坐标为,
当y=时,由=,整理得,x2﹣2x﹣13=0,
解得,x1=1,x2=,
∴N或N,
综上所述,点N的坐标为或或.
13.解:(1)在y=x2+2x中,令y=0,得x2+2x=0,
解得:x1=0,x2=﹣4,
∴A(﹣4,0),
设直线AB的解析式为y=kx+b,
∵A(﹣4,0),B(2,6),
∴,
解得:,
∴直线AB的函数解析式为:y=x+4;
(2)如图1,∵y=x2+2x=(x+2)2﹣2,
∴该抛物线对称轴为直线x=﹣2,
∴直线x=﹣2与直线AB交于点Q,
∵点A(﹣4,0)与点O(0,0)关于直线x=﹣2对称,
∴BQ+QO+OB=BQ+QA+OB=AB+OB,此时,△OBQ的周长最小,
∵AB==6,OB==2,
∴△OBQ的周长取最小2时,点Q(﹣2,2),
此时,S△BOQ=S△ABO﹣S△AQO=OA yB﹣OA yQ=OA (yB﹣yQ)=×4×(6﹣2)=8.
(3)点A、O、B、N为顶点的四边形是平行四边形时,设N(m,n),分三种情况:
①以AN、BO为对角线,此时AN中点与CO中点重合,如图2,
∵A(﹣4,0)、O(0,0),B(2,6),
∴AN的中点为(,),OC中点为(,),
∴,
解得:,
∴N(6,6),
②以AB、NO为对角线,此时AB中点与NO中点重合,如图3,
同理可得:,
解得:,
∴N(﹣2,6),
③以AO、BN为对角线,此时AO中点与BN中点重合,如图4,
同理可得:,
解得:,
∴N(﹣6,﹣6),
综上所述,点A、O、C、N为顶点的四边形是平行四边形,
点N的坐标为:(6,6)或(﹣2,6)或(﹣6,﹣6).
故答案为:(6,6)或(﹣2,6)或(﹣6,﹣6).
14.解:(1)∵直线y=﹣x+c与x轴交于点B(3,0),与y轴交于点C,
∴﹣3+c=0,
解得c=3,
∴C(0,3),
∵抛物线经过B,C,
∴,
解得,
∴抛物线的解析式为y=﹣x2+2x+3,
令y=0,得到﹣x2+2x+3=0,解得x=﹣1或3,
∴A(﹣1,0).
(2)法一:如图,过点P作PG∥x轴交直线BC于点G,设P(m,﹣m2+2m+3).
∵PG∥x轴,
∵P是直线BC上方抛物线上一动点,
∴0<m<3,
由直线BC:y=﹣x+3知,G点坐标为(m2﹣2m,﹣m2+2m+3),
故PG=m﹣(m2﹣2m)=﹣m2+3m,
∵AB=4,PG=﹣m2+3m,
∴,
∵,
∴时,t有最大值,最大值为,此时,.
法二:如图2,连接AC,PC,PB,过点A作AE⊥BC于E,过点P作PF⊥BC于F.设P(m,﹣m2+2m+3).
∵AE∥PF,
∵,,
∴,
∵,
∵S△PBC=S△PCO+S△PBO﹣S△BOC==,
∴,
∵,
∴时,t有最大值,最大值为,此时,.
15.解:(1)∵直线y=﹣x﹣1经过点A,
∴令y=0,则0=﹣x﹣1,
∴x=﹣1,
∴A(﹣1,0),
将A(﹣1,0),C(0,3)代入y=ax2+2x+c得
,
解得,
∴抛物线的解析式为:y=﹣x2+2x+3;
(2)如图,过点P作PE⊥x轴,交x轴于点G,交AD于点F,作DE⊥PF于E,
由题意得,
,
解得:x1=﹣1,x2=4,
当x=4时,y=﹣5,
∴D(4,﹣5),
设P(m,﹣m2+2m+3),F(m,﹣m﹣1),
∴PF=﹣m2+2+3﹣(﹣m﹣1)=﹣m2+3m+4,
∴S△PAD=S△PAF+S△PDF=PF AG+PF DE=PF(AG+DE),
∵AG+DE=|xD﹣xA|=5,
∴S△PAD=PF,
∴当PF取最大值时,S△PAD的值最大,
PF=﹣m2+3m+4=﹣(m﹣)2+,
∴PF最大值为,
则△PAD的面积的最大值为=.
16.解:(1)把A(0,2)代入y=a(x﹣2)2﹣2,得a=1.
∴抛物线的解析式为y=(x﹣2)2﹣2=x2﹣4x+2.
(2)由(1)知,抛物线的对称轴为x=2,
设,依题意,
知,
解得.
把代入抛物线,得,
所以P,Q的坐标是.
(3)由(1)知B(2,﹣2),
当直线y=﹣x+m经过点B时,得m=0,
当直线y=﹣x+m经过点Q时,得,
所以m的取值范围是:.
设直线BQ的解析式为:y=kx+b,将B,Q的坐标代入,
得,所以直线BQ的解析式为:.
设直线BQ交y轴于点E,则E(0,﹣5),,
∴.
当m=0时,S△BDQ最小值为,
当时,S△BDQ最大值为.
17.解:(1)将B(1,0)、C(0,﹣2)代入中得:,
∴,
∴该抛物线的对称轴为,
∵B(1,0),
∴A(4,0),
令直线AC的解析式为y=kx+b,将A(4,0),C(0,﹣2),
代入得:,
∴,
(2)令,连接OQ,
则,,
∴,
∵=﹣m2+4m=﹣(m﹣2)2+4,
∵﹣1<0,
∴m=2时,△AQC的面积最大为4,
此时Q(2,1),
(3)存在点M使以A,M,N为顶点的三角形与△OAC相似,
设,则N(a,0),分两种情况,
①若△NMA∽△OAC,则,
即,
则|16﹣4a|=|a2﹣5a+4|,
当a2﹣5a+4=16﹣4a时,得a1=4(舍),a2=﹣3,
当a2﹣5a+4=4a﹣16时,a1=5,a2=4(舍),
即M1(﹣3,﹣14),M2(5,﹣2),
②若△NAM∽△OAC,则,
即,
则|2a2﹣10a+8|=|8﹣2a|,
当2a2﹣10a+8=8﹣2a时,a1=0,a2=4(舍),即M3(0,﹣2),
当2a2﹣10a+8=2a﹣8时,a1=2,a2=4(舍),即M4(2,1),
综上所述,M1(﹣3,﹣14),M2(5,﹣2),M3(0,﹣2),M4(2,1).
18.(1)把A(﹣1,0),B(3,0)两点分别代数入y=ax2+bx+3得:
a﹣b+3=0,9a+3b+3=0,
解得:a=﹣1,b=2,
∴抛物线解析式为:y=﹣x2+2x+3,
∴点D的坐标为(0,3),
抛物线的对称轴为直线x=1,顶点E(1,4),
∵C、D两点关于抛物线的对称轴对称,
∴点C(2,3),
将点A、C的坐标代入一次函数表达式得:,
解得,
∴直线AC的表达式为y=x+1,
(2)①∵点P的横坐标为x.则点P,H的坐标分别为
P(x,﹣x2+2x+3),H(x,x+1),
∴PH=﹣x2+2x+3﹣x﹣1=﹣x2+x+2;
②∵△PAC的面积=S△PHA+S△PHC=(xC﹣xA)
=,
∴﹣x2+x+2=,
解得:x=或x=(不合题意,舍去),
当x=时,y=﹣x2+2x+3=,
∴P点的坐标为(,).
19.解:(1)∵抛物线C1:y=﹣x2+x+3与x轴交于A、B两点,
∴当y=0时,﹣x2+x+3=0,解得x1=4,x2=﹣,
∴A(﹣,0),B(4,0),
当x=0时,y=3,
∴C(0,3),
设直线BC的函数解析式为:y=kx+b,
,
解得,
∴直线BC的函数解析式为:y=﹣x+3;
(2)设点P(m,﹣),
∵PE∥x轴,
∴点E的纵坐标为﹣,
∵点E在直线BC上,
∴点E的横坐标为,
∴PE=m﹣()=﹣,
当m=﹣=2时,PE最大值为﹣=,
此时点P(2,);
(3)当OC为边时,如图,则MN∥OC,MN=OC=3,
设M(t,﹣t+3),则N(t,﹣t2+
),
∴|﹣t+3﹣(﹣t2+
)|=3,
∴||=3,
∴或.
解得t1=2+,t2=2﹣,
∴点M(2+,)或(2﹣,),
当OC为对角线时,
设M(t,﹣t+3),由M点平移到点C,点O平移到点N可知:N(﹣t,
),
∴﹣t2﹣t+3=+1,
∴t2+4t﹣4=0,
解得t=﹣2±2,
∴点M(﹣2+2,)或(﹣2﹣2,),
综上所述:点M(2+,)或(2﹣,)或(﹣2+2,)或(﹣2﹣2,).
20.解:(1)由题意得:3x+20+GC=100,
解得:GC=(80﹣3x)m,
∵BC=BG+GC=10+80﹣3x,
而0<BC≤30,即0<10+80﹣3x≤30,解得20≤x<30,
矩形CDHG面积=GC CD=(80﹣3x)x=125,解得x=25或(舍去),
∴CD长为25m;
(2)设矩形ABCD的面积为s,则s=BC CD=x(10+80﹣3x)=﹣3x2+90x=﹣3(x﹣15)2+675,
∵﹣3<0,故抛物线开口向下,
而20≤x<30,
当x>15时,s随x的增大而减小,
故当x=20(m)时,s取得最大值为﹣3×(20﹣15)2+675=600(m2).
答:当CD长为20m时,矩形ABCD的面积最大,最大面积是600m2.
同课章节目录
