2021-2022学年八年级数学上册 华东师大版13.3.2 等腰三角形的判定同步练习(含答案)
文档属性
| 名称 | 2021-2022学年八年级数学上册 华东师大版13.3.2 等腰三角形的判定同步练习(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 577.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-03 16:11:16 | ||
图片预览



文档简介
2021-2022学年八年级数学上册(华东师大版)
13.3.2等腰三角形的判定-同步练习
时间:60分钟
一、单选题
1.已知:如图,经过线段一端点A有一直线l,直线上l存在点C,使为等腰三角形,这样的点C有(
)个.
A.2
B.3
C.4
D.5
2.如图,是的角平分线,交于E,若,则(
).
A.8
B.11
C.10
D.9
3.如图所示的正方形网格中,网格的交点称为格点,已知,是两格点,如果也是图中的格点,且使得为等腰三角形,则符合条件的点的个数是(
)
A.6
B.7
C.8
D.9
4.如图,将两个全等的有一个角为30°的直角三角形拼成如下图形,其中两条长直角边在同一直线上,则图中等腰三角形的个数是(
)
A.4
B.3
C.2
D.1
5.下列说法:
①三角形按边分类可分为三边不等的三角形、等腰三角形和等边三角形;
②等边三角形是特殊的等腰三角形;
③等腰三角形是特殊的等边三角形;
④有两边相等的三角形一定是等腰三角形;
其中,说法正确的个数是(
)
A.1个
B.2个
C.3个
D.4个
6.如图,等边三角形的三条角平分线相交于点O,交于点D,交于点E,那么这个图形中的等腰三角形共有(
)个
A.4
B.5
C.6
D.7
7.如图,已知OC平分∠AOB,CD//OB,若OD=3
cm,则CD等于:(
)
A.1.5cm
B.2cm
C.3cm
D.4cm
8.在平面直角坐标系中,点A坐标为(2,2),点P在x轴上运动,当以点A,P、O为顶点的三角形为等腰三角形时,点P的个数为( )
A.2个
B.3个
C.4个
D.5个
二、填空题
9.如图,在下列三角形中,若AB=AC,则能被一条直线分成两个小等腰三角形的是____________.(填序号)
10.等腰三角形的判定定理是______________________.
11.已知:如图,中,分别是和的平分线,过O点的直线分别交、于点D、E,且.若,则的周长为______.
12.已知、,点在轴上,若是等腰三角形,则满足这样条件的有________个.
13.如图,∠AOE=∠BOE=15°,EF∥OB,EC⊥OB于C,若EC=1,则OF=_____.
14.在平面直角坐标系xOy中,已知点A(2,3),在坐标轴上找一点P,使得AOP是等腰三角形,则这样的点P共有_____个.
15.已知:如图,O为坐标原点,四边形OABC为矩形,A(10,0),C(0,4),点D是OA的中点,点P在BC上运动,当△ODP是腰长为5的等腰三角形时,则P点的坐标为__________.
16.如图,在中,的中垂线交于点P,若,则的度数为________.
三、解答题
17.如图,若是等边三角形,是的平分线,延长到点E,使,求的长度.
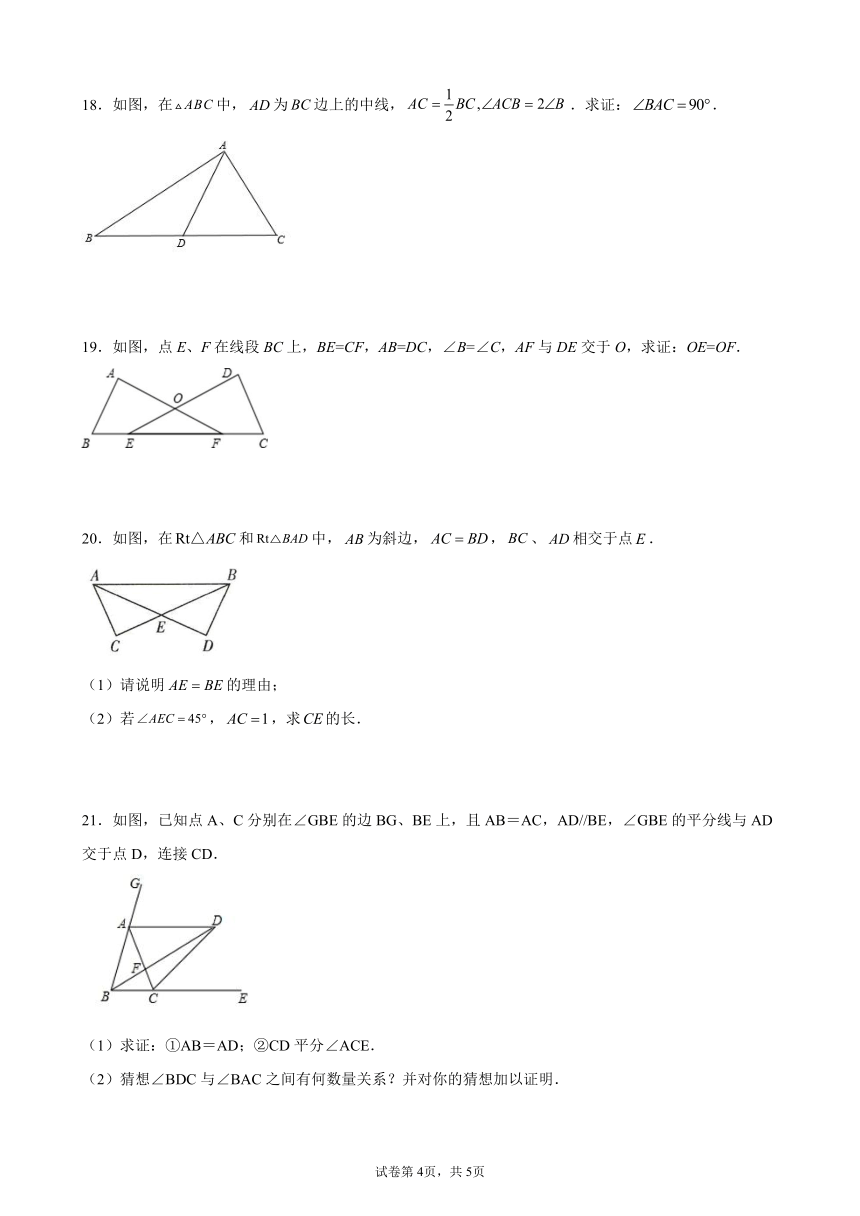
18.如图,在中,为边上的中线,.求证:.
19.如图,点E、F在线段BC上,BE=CF,AB=DC,∠B=∠C,AF与DE交于O,求证:OE=OF.
20.如图,在和中,为斜边,,、相交于点.
(1)请说明的理由;
(2)若,,求的长.
21.如图,已知点A、C分别在∠GBE的边BG、BE上,且AB=AC,AD//BE,∠GBE的平分线与AD交于点D,连接CD.
(1)求证:①AB=AD;②CD平分∠ACE.
(2)猜想∠BDC与∠BAC之间有何数量关系?并对你的猜想加以证明.
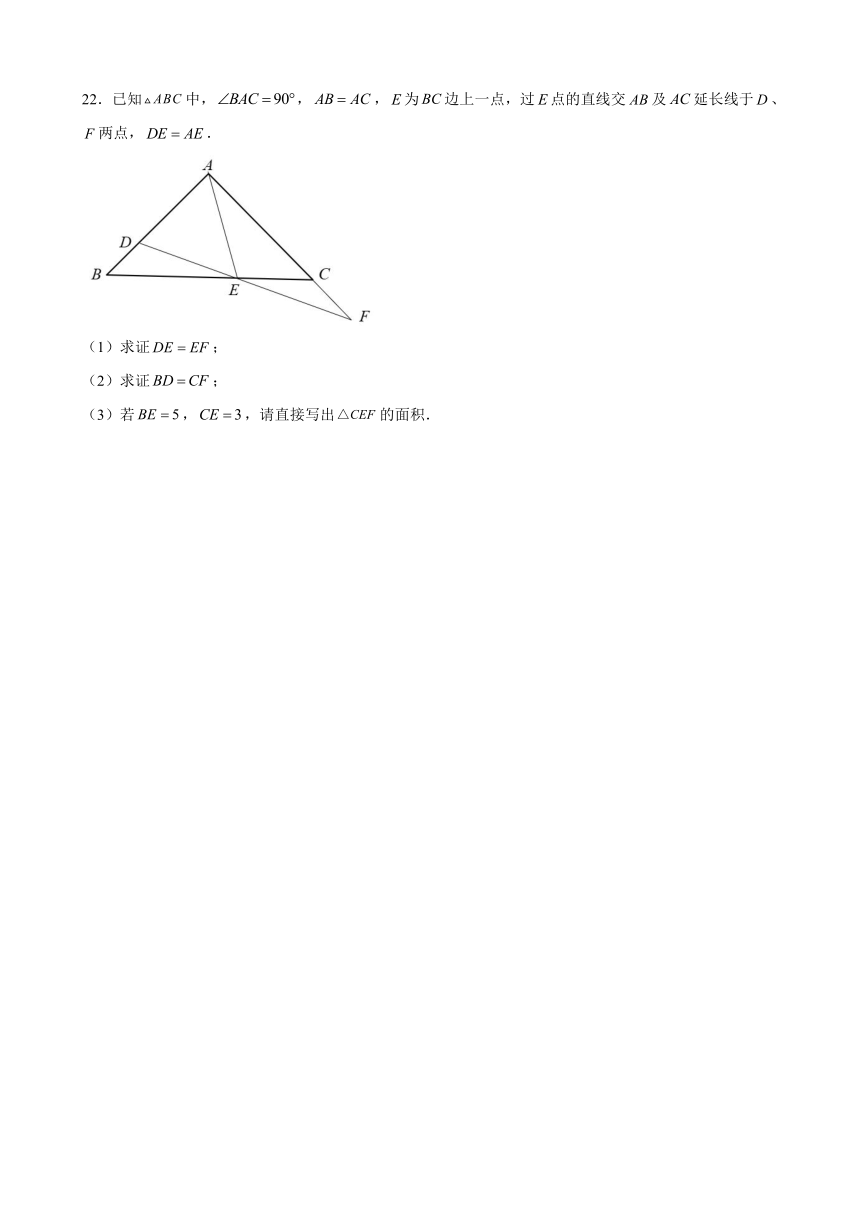
22.已知中,,,为边上一点,过点的直线交及延长线于、两点,.
(1)求证;
(2)求证;
(3)若,,请直接写出的面积.
试卷第1页,共3页
参考答案
1.C
【解析】解:如图所示,以B为圆心,以AB的长为半径画弧与直线l交于点D,此时AB=BD,同理以A为圆心以AB的长为半径与直线l交于E、C,此时AC=AB,AE=AB,再作AB的垂直平分线与直线l交于点F,此时AF=BF,
∴一共有4个点满足题意,
故选C.
2.A
【解析】解:∵是的角平分线,
∴∠DCB=∠DCE,
∵,
∴∠DCB=∠EDC,
∴∠EDC=∠DCE,
∴CE=DE=3cm,
∴AC=AE+CE=5+3=8cm.
故选择A.
3.C
【解析】解:如图所示,①为等腰底边时,符合条件的点有4个;
②为等腰其中的一条腰时,符合条件的点有4个.
故选:.
4.B
【解析】如图,
∵将两个全等的有一个角为30°的直角三角形拼在一起,其中两条较长直角边在同一条直线上.
∴EF∥DG,∠E=∠D=60°,
∴∠ENM=∠D=60°,∠MGD=∠E=60°,
∴EM=NM=EN,DM=GM=DG,
∴△MEN,△MDG是等边三角形.
∵∠A=∠B=30°,
∴MA=MB,
∴△ABM是等腰三角形.
∴图中等腰三角形有3个.
故选:B.
5.B
【解析】①三角形按边分类可分为三边不等的三角形、等腰三角形;故原说法错误.
②等边三角形是特殊的等腰三角形;正确.
③等边三角形是特殊的等腰三角形;故原说法错误.
④有两边相等的三角形一定是等腰三角形;正确,
故选:B.
6.D
【解析】解:①∵△ABC为等边三角形,
∴AB=AC,
∴△ABC为等腰三角形;
②∵BO,CO,AO分别是三个角的角平分线,
∴∠ABO=∠CBO=∠BAO=∠CAO=∠ACO=∠BCO,
∴AO=BO,AO=CO,BO=CO,
∴△AOB为等腰三角形;
③△AOC为等腰三角形;
④△BOC为等腰三角形;
⑤∵OD∥AB,OE∥AC,
∴∠ABC=∠ODE,∠ACB=∠OED,
∵∠ABC=∠ACB,
∴∠ODE=∠OED,
∴△DOE为等腰三角形;
⑥∵OD∥AB,OE∥AC,
∴∠BOD=∠ABO,∠COE=∠ACO,
∵∠DBO=∠ABO,∠ECO=∠ACO,
∴∠BOD=∠DBO,∠COE=∠ECO,
∴△BOD为等腰三角形;
⑦△COE为等腰三角形.
故选:D.
7.C
【解析】∵OC平分∠AOB,
∴∠AOC=∠BOC;
又∵CD∥OB,
∴∠C=BOC,
∴∠C=∠AOC;
故选C.
8.C
【解析】如图,当OA=OP时,可得P1、P2满足条件,
当OA=AP时,可得P3满足条件,
当AP=OP时,可得P4满足条件,
故选C.
9.(1)(3)(4)
【解析】由题意知,要求“被一条直线分成两个小等腰三角形”,
(1)中分成的两个等腰三角形的角的度数分别为:36°,36°,108°和36°,72°72°;
(2)不能;
(3)直角三角形的斜边上的中线把它还分为了两个等腰三角形;
(4)中分成的为36°,72°,72°和36°,36°,108°.
故应填①③④.
10.等角对等边
【解析】解:等腰三角形的判定定理是:如果一个三角形有两个角相等,那么这两个角所对的边也相等,即等角对等边
故答案为:等角对等边.
11.
【解析】∵,
∴,
又∵是的角平分线,
∴,
∴,
∴,
同理,
∴的周长.
故答案为:14cm
12.
【解析】以A为圆心,以AB为半径画弧,交x轴于C1点,此时AC=AB;
以B为圆心,以AB为半径画弧,交x轴于C2,C3点,此时BC=AB;
作AB的垂直平分线交x轴于C4点,此时AC=BC.
故答案为4.
13.2
【解析】作EH⊥OA于H.
∵∠AOE=∠BOE=15°,EC⊥OB,EH⊥OA,∴EH=EC=1,∠AOB=30°.
∵EF∥OB,∴∠EFH=∠AOB=30°,∠FEO=∠BOE,∴EF=2EH=2,∠FEO=∠FOE,∴OF=EF=2.
故答案为2.
14.8
【解析】作出图形,如图,可知使得△AOP是等腰三角形的点P共有8个.
故答案是:8
15.P(3,4)或(2,4)或(8,4)
【解析】由题意,当△ODP是腰长为5的等腰三角形时,有三种情况:
(1)如图所示,PD=OD=5,点P在点D的左侧.
过点P作PE⊥x轴于点E,则PE=4.
在Rt△PDE中,由勾股定理得:DE=,
∴OE=OD-DE=5-3=2,
∴此时点P坐标为(2,4);
(2)如图所示,OP=OD=5.
过点P作PE⊥x轴于点E,则PE=4.
在Rt△POE中,由勾股定理得:
OE=,
∴此时点P坐标为(3,4);
(3)如图所示,PD=OD=5,点P在点D的右侧.
过点P作PE⊥x轴于点E,则PE=4.
在Rt△PDE中,由勾股定理得:
DE=,
∴OE=OD+DE=5+3=8,
∴此时点P坐标为(8,4).
综上所述,点P的坐标为:(2,4)或(3,4)或(8,4).
16.
【解析】连接
分别为的垂直平分线,
,
是等腰三角形
故答案为:
17.9
【解析】解:∵是等边三角形,
∴,
∵是的平分线,
∴,
∵,
∴,
∴.
18.见解析.
【解析】证明:如图,
作的平分线交于点E,连接,
∵,
∴,
∴,
又∵为边上的中线,点D为中点,
∴,
又∵,
∴,
在和中,
∴,
∴.
19.详见解析.
【解析】证明:∵BE=CF,
∴BE+EF=CF+EF,
即BF=CE,
又∵AB=DC,∠B=∠C,
∴△ABF≌△DCE,
∴∠AFB=∠DEC,
∴OE=OF.
20.(1)见解析;(2)CE=1.
【解析】(1)证明:在和中,
∵与是对顶角,
∴.
∵,,
∴≌(AAS).
∴.
(2)∵,,
∴,
∴
,
∴.
21.(1)①见解析;②见解析;(2),证明见解析
【解析】(1)证明:平分
∴∠ABD=∠DBC
∴∠ADB=∠DBC
∴∠ABD=∠ADB,
;
②,
平分
(2)
理由:∵CD、BD分别平分∠ACE,∠ABE,
,∠DBC=∠ABC,
又
又∵∠BDC+∠DBC=∠DCE
∴∠BDC+∠ABC=∠ACE,
∴∠BDC+∠ABC=∠ABC+∠BAC,
∴.
22.(1)证明见解析;(2)证明见解析;(3)
【解析】证明:(1)
(2)如图,过作交于,
,,
,
,
,
,
在与中,
(3)过作于,
,
,
,
,
,
,
,
,
答案第1页,共2页
答案第1页,共2页
13.3.2等腰三角形的判定-同步练习
时间:60分钟
一、单选题
1.已知:如图,经过线段一端点A有一直线l,直线上l存在点C,使为等腰三角形,这样的点C有(
)个.
A.2
B.3
C.4
D.5
2.如图,是的角平分线,交于E,若,则(
).
A.8
B.11
C.10
D.9
3.如图所示的正方形网格中,网格的交点称为格点,已知,是两格点,如果也是图中的格点,且使得为等腰三角形,则符合条件的点的个数是(
)
A.6
B.7
C.8
D.9
4.如图,将两个全等的有一个角为30°的直角三角形拼成如下图形,其中两条长直角边在同一直线上,则图中等腰三角形的个数是(
)
A.4
B.3
C.2
D.1
5.下列说法:
①三角形按边分类可分为三边不等的三角形、等腰三角形和等边三角形;
②等边三角形是特殊的等腰三角形;
③等腰三角形是特殊的等边三角形;
④有两边相等的三角形一定是等腰三角形;
其中,说法正确的个数是(
)
A.1个
B.2个
C.3个
D.4个
6.如图,等边三角形的三条角平分线相交于点O,交于点D,交于点E,那么这个图形中的等腰三角形共有(
)个
A.4
B.5
C.6
D.7
7.如图,已知OC平分∠AOB,CD//OB,若OD=3
cm,则CD等于:(
)
A.1.5cm
B.2cm
C.3cm
D.4cm
8.在平面直角坐标系中,点A坐标为(2,2),点P在x轴上运动,当以点A,P、O为顶点的三角形为等腰三角形时,点P的个数为( )
A.2个
B.3个
C.4个
D.5个
二、填空题
9.如图,在下列三角形中,若AB=AC,则能被一条直线分成两个小等腰三角形的是____________.(填序号)
10.等腰三角形的判定定理是______________________.
11.已知:如图,中,分别是和的平分线,过O点的直线分别交、于点D、E,且.若,则的周长为______.
12.已知、,点在轴上,若是等腰三角形,则满足这样条件的有________个.
13.如图,∠AOE=∠BOE=15°,EF∥OB,EC⊥OB于C,若EC=1,则OF=_____.
14.在平面直角坐标系xOy中,已知点A(2,3),在坐标轴上找一点P,使得AOP是等腰三角形,则这样的点P共有_____个.
15.已知:如图,O为坐标原点,四边形OABC为矩形,A(10,0),C(0,4),点D是OA的中点,点P在BC上运动,当△ODP是腰长为5的等腰三角形时,则P点的坐标为__________.
16.如图,在中,的中垂线交于点P,若,则的度数为________.
三、解答题
17.如图,若是等边三角形,是的平分线,延长到点E,使,求的长度.
18.如图,在中,为边上的中线,.求证:.
19.如图,点E、F在线段BC上,BE=CF,AB=DC,∠B=∠C,AF与DE交于O,求证:OE=OF.
20.如图,在和中,为斜边,,、相交于点.
(1)请说明的理由;
(2)若,,求的长.
21.如图,已知点A、C分别在∠GBE的边BG、BE上,且AB=AC,AD//BE,∠GBE的平分线与AD交于点D,连接CD.
(1)求证:①AB=AD;②CD平分∠ACE.
(2)猜想∠BDC与∠BAC之间有何数量关系?并对你的猜想加以证明.
22.已知中,,,为边上一点,过点的直线交及延长线于、两点,.
(1)求证;
(2)求证;
(3)若,,请直接写出的面积.
试卷第1页,共3页
参考答案
1.C
【解析】解:如图所示,以B为圆心,以AB的长为半径画弧与直线l交于点D,此时AB=BD,同理以A为圆心以AB的长为半径与直线l交于E、C,此时AC=AB,AE=AB,再作AB的垂直平分线与直线l交于点F,此时AF=BF,
∴一共有4个点满足题意,
故选C.
2.A
【解析】解:∵是的角平分线,
∴∠DCB=∠DCE,
∵,
∴∠DCB=∠EDC,
∴∠EDC=∠DCE,
∴CE=DE=3cm,
∴AC=AE+CE=5+3=8cm.
故选择A.
3.C
【解析】解:如图所示,①为等腰底边时,符合条件的点有4个;
②为等腰其中的一条腰时,符合条件的点有4个.
故选:.
4.B
【解析】如图,
∵将两个全等的有一个角为30°的直角三角形拼在一起,其中两条较长直角边在同一条直线上.
∴EF∥DG,∠E=∠D=60°,
∴∠ENM=∠D=60°,∠MGD=∠E=60°,
∴EM=NM=EN,DM=GM=DG,
∴△MEN,△MDG是等边三角形.
∵∠A=∠B=30°,
∴MA=MB,
∴△ABM是等腰三角形.
∴图中等腰三角形有3个.
故选:B.
5.B
【解析】①三角形按边分类可分为三边不等的三角形、等腰三角形;故原说法错误.
②等边三角形是特殊的等腰三角形;正确.
③等边三角形是特殊的等腰三角形;故原说法错误.
④有两边相等的三角形一定是等腰三角形;正确,
故选:B.
6.D
【解析】解:①∵△ABC为等边三角形,
∴AB=AC,
∴△ABC为等腰三角形;
②∵BO,CO,AO分别是三个角的角平分线,
∴∠ABO=∠CBO=∠BAO=∠CAO=∠ACO=∠BCO,
∴AO=BO,AO=CO,BO=CO,
∴△AOB为等腰三角形;
③△AOC为等腰三角形;
④△BOC为等腰三角形;
⑤∵OD∥AB,OE∥AC,
∴∠ABC=∠ODE,∠ACB=∠OED,
∵∠ABC=∠ACB,
∴∠ODE=∠OED,
∴△DOE为等腰三角形;
⑥∵OD∥AB,OE∥AC,
∴∠BOD=∠ABO,∠COE=∠ACO,
∵∠DBO=∠ABO,∠ECO=∠ACO,
∴∠BOD=∠DBO,∠COE=∠ECO,
∴△BOD为等腰三角形;
⑦△COE为等腰三角形.
故选:D.
7.C
【解析】∵OC平分∠AOB,
∴∠AOC=∠BOC;
又∵CD∥OB,
∴∠C=BOC,
∴∠C=∠AOC;
故选C.
8.C
【解析】如图,当OA=OP时,可得P1、P2满足条件,
当OA=AP时,可得P3满足条件,
当AP=OP时,可得P4满足条件,
故选C.
9.(1)(3)(4)
【解析】由题意知,要求“被一条直线分成两个小等腰三角形”,
(1)中分成的两个等腰三角形的角的度数分别为:36°,36°,108°和36°,72°72°;
(2)不能;
(3)直角三角形的斜边上的中线把它还分为了两个等腰三角形;
(4)中分成的为36°,72°,72°和36°,36°,108°.
故应填①③④.
10.等角对等边
【解析】解:等腰三角形的判定定理是:如果一个三角形有两个角相等,那么这两个角所对的边也相等,即等角对等边
故答案为:等角对等边.
11.
【解析】∵,
∴,
又∵是的角平分线,
∴,
∴,
∴,
同理,
∴的周长.
故答案为:14cm
12.
【解析】以A为圆心,以AB为半径画弧,交x轴于C1点,此时AC=AB;
以B为圆心,以AB为半径画弧,交x轴于C2,C3点,此时BC=AB;
作AB的垂直平分线交x轴于C4点,此时AC=BC.
故答案为4.
13.2
【解析】作EH⊥OA于H.
∵∠AOE=∠BOE=15°,EC⊥OB,EH⊥OA,∴EH=EC=1,∠AOB=30°.
∵EF∥OB,∴∠EFH=∠AOB=30°,∠FEO=∠BOE,∴EF=2EH=2,∠FEO=∠FOE,∴OF=EF=2.
故答案为2.
14.8
【解析】作出图形,如图,可知使得△AOP是等腰三角形的点P共有8个.
故答案是:8
15.P(3,4)或(2,4)或(8,4)
【解析】由题意,当△ODP是腰长为5的等腰三角形时,有三种情况:
(1)如图所示,PD=OD=5,点P在点D的左侧.
过点P作PE⊥x轴于点E,则PE=4.
在Rt△PDE中,由勾股定理得:DE=,
∴OE=OD-DE=5-3=2,
∴此时点P坐标为(2,4);
(2)如图所示,OP=OD=5.
过点P作PE⊥x轴于点E,则PE=4.
在Rt△POE中,由勾股定理得:
OE=,
∴此时点P坐标为(3,4);
(3)如图所示,PD=OD=5,点P在点D的右侧.
过点P作PE⊥x轴于点E,则PE=4.
在Rt△PDE中,由勾股定理得:
DE=,
∴OE=OD+DE=5+3=8,
∴此时点P坐标为(8,4).
综上所述,点P的坐标为:(2,4)或(3,4)或(8,4).
16.
【解析】连接
分别为的垂直平分线,
,
是等腰三角形
故答案为:
17.9
【解析】解:∵是等边三角形,
∴,
∵是的平分线,
∴,
∵,
∴,
∴.
18.见解析.
【解析】证明:如图,
作的平分线交于点E,连接,
∵,
∴,
∴,
又∵为边上的中线,点D为中点,
∴,
又∵,
∴,
在和中,
∴,
∴.
19.详见解析.
【解析】证明:∵BE=CF,
∴BE+EF=CF+EF,
即BF=CE,
又∵AB=DC,∠B=∠C,
∴△ABF≌△DCE,
∴∠AFB=∠DEC,
∴OE=OF.
20.(1)见解析;(2)CE=1.
【解析】(1)证明:在和中,
∵与是对顶角,
∴.
∵,,
∴≌(AAS).
∴.
(2)∵,,
∴,
∴
,
∴.
21.(1)①见解析;②见解析;(2),证明见解析
【解析】(1)证明:平分
∴∠ABD=∠DBC
∴∠ADB=∠DBC
∴∠ABD=∠ADB,
;
②,
平分
(2)
理由:∵CD、BD分别平分∠ACE,∠ABE,
,∠DBC=∠ABC,
又
又∵∠BDC+∠DBC=∠DCE
∴∠BDC+∠ABC=∠ACE,
∴∠BDC+∠ABC=∠ABC+∠BAC,
∴.
22.(1)证明见解析;(2)证明见解析;(3)
【解析】证明:(1)
(2)如图,过作交于,
,,
,
,
,
,
在与中,
(3)过作于,
,
,
,
,
,
,
,
,
答案第1页,共2页
答案第1页,共2页
