2021-2022学年北师大版八年级数学上册第1章勾股定理 单元能力达标测评(word版、含解析)
文档属性
| 名称 | 2021-2022学年北师大版八年级数学上册第1章勾股定理 单元能力达标测评(word版、含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 272.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-03 11:11:46 | ||
图片预览

文档简介
2021-2022学年北师大版八年级数学上册《第1章勾股定理》单元能力达标测评(附答案)
一.选择题(共10小题,满分30分)
1.如图,在△ABC中,∠ACB=90°,AD平分∠BAC交BC于点D,BC=8cm,AC=6cm,则BD的长为( )
A.3cm
B.4cm
C.5cm
D.6cm
2.国庆假期中,小华与同学去玩探宝游戏,按照探宝图,他们从门口A处出发先往东走8km,又往北走2km,遇到障碍后又往西走3km,再向北走到6km处往东拐,仅走了1km,就找到了宝藏,则门口A到藏宝点B的直线距离是( )
A.20km
B.14km
C.11km
D.10km
3.如图,在Rt△ABC中,∠ACB=90°,以△ABC的各边为边在△ABC外作三个正方形,S1,S2,S3分别表示这三个正方形的面积,若S1=3,S2=10,则S3=( )
A.5
B.7
C.13
D.15
4.下面四组线段中,可以构成直角三角形的是( )
A.2,3,4
B.4,5,6
C.3,4,6
D.6,8,10
5.如图,四边形ABCD中,AB=3cm,AD=4cm,BC=13cm,CD=12cm,且∠A=90°,则四边形ABCD的面积为( )
A.12cm2
B.18cm2
C.22cm2
D.36cm2
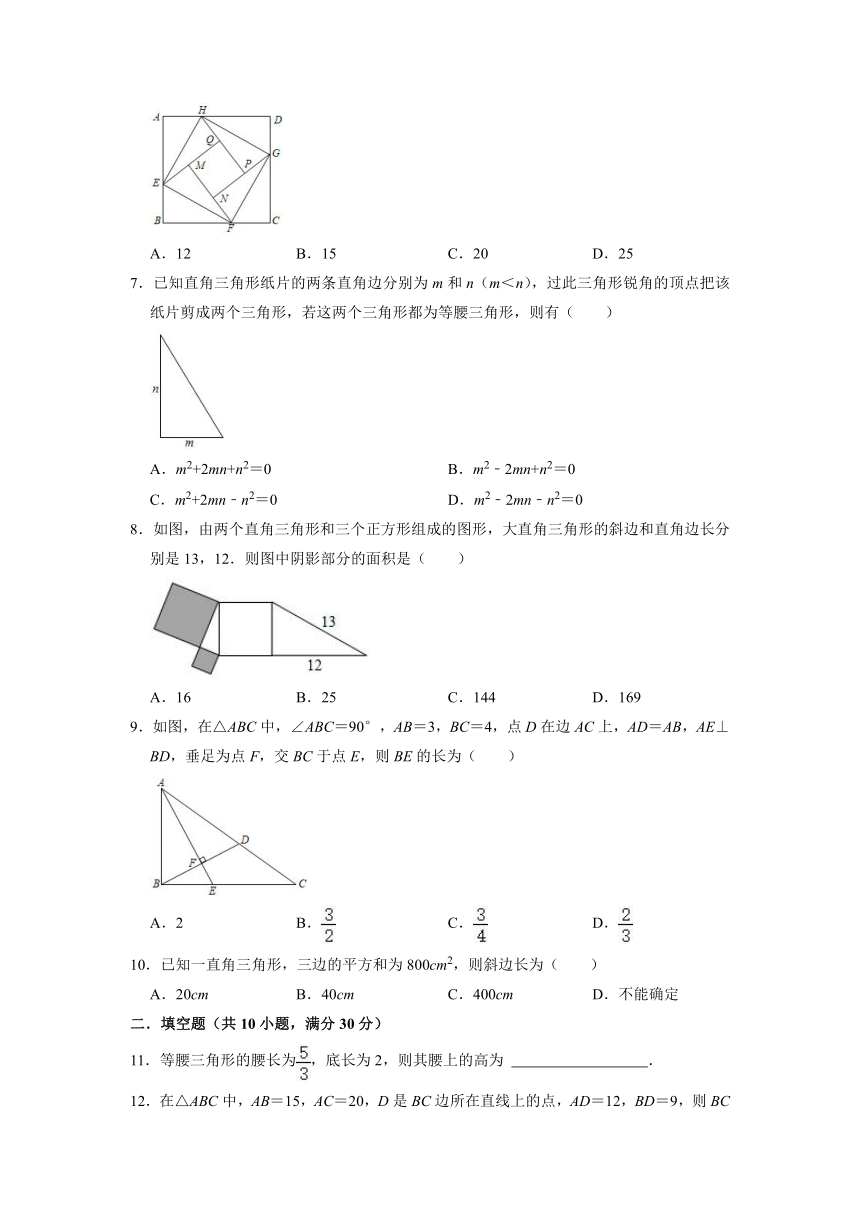
6.如图是由“赵爽弦图”变化得到的,它由八个全等的直角三角形拼接而成,记图中正方形ABCD,正方形EFGH,正方形MNPQ的面积分别为S1,S2,S3,若S1+S2+S3=45,则S2的值是( )
A.12
B.15
C.20
D.25
7.已知直角三角形纸片的两条直角边分别为m和n(m<n),过此三角形锐角的顶点把该纸片剪成两个三角形,若这两个三角形都为等腰三角形,则有( )
A.m2+2mn+n2=0
B.m2﹣2mn+n2=0
C.m2+2mn﹣n2=0
D.m2﹣2mn﹣n2=0
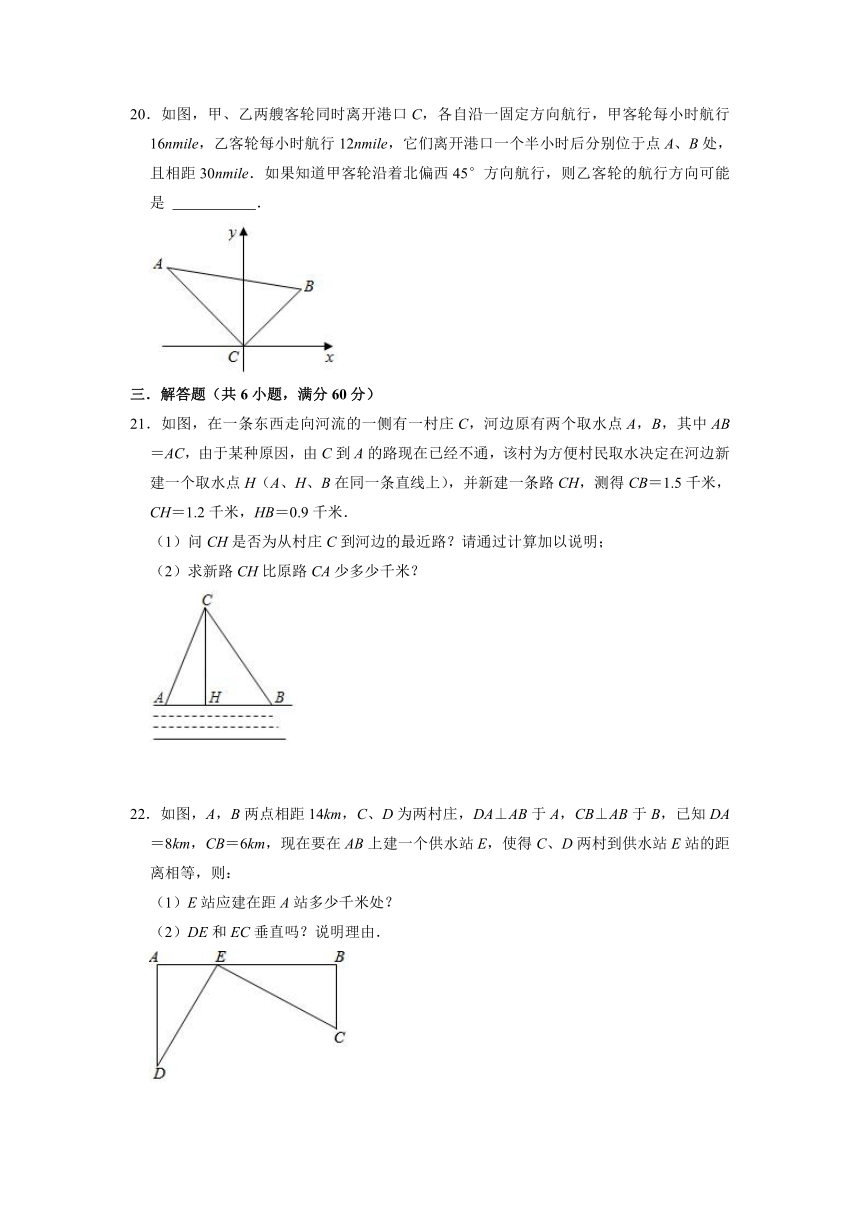
8.如图,由两个直角三角形和三个正方形组成的图形,大直角三角形的斜边和直角边长分别是13,12.则图中阴影部分的面积是( )
A.16
B.25
C.144
D.169
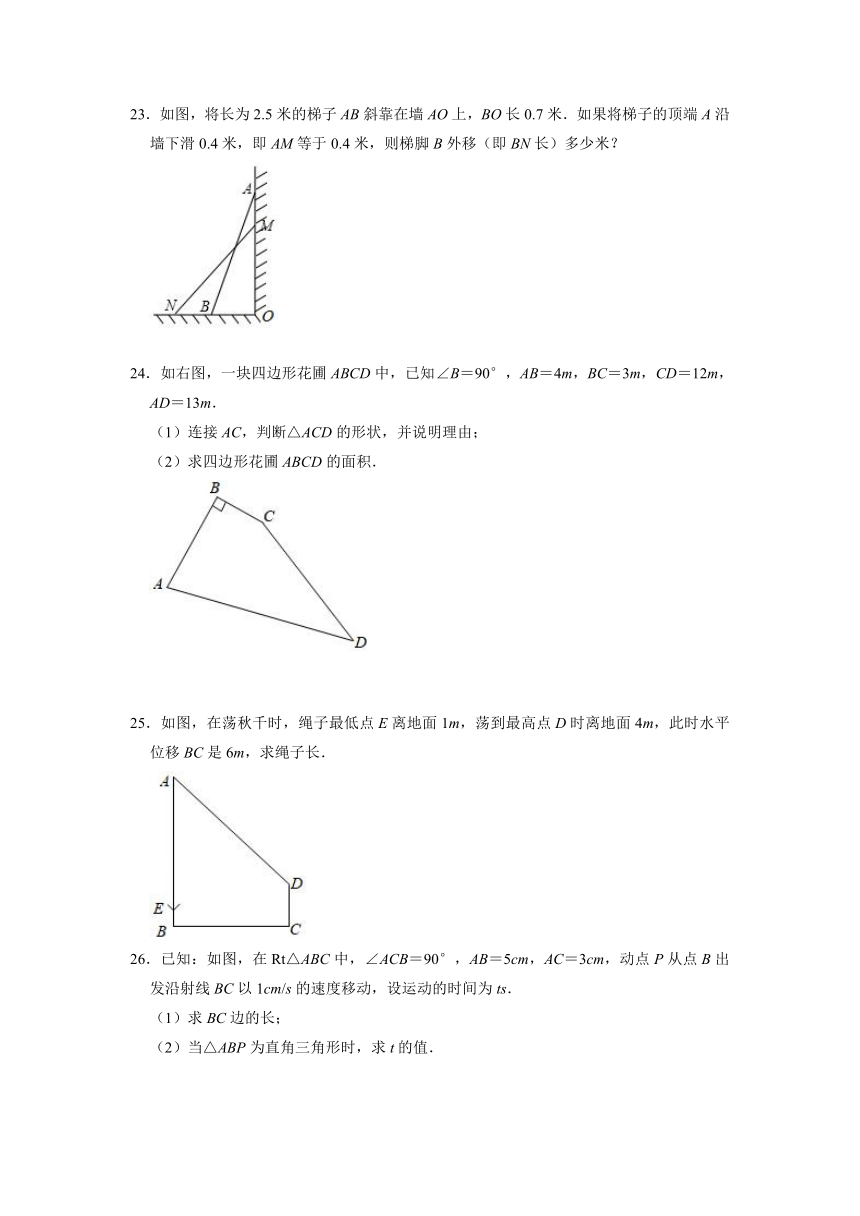
9.如图,在△ABC中,∠ABC=90°,AB=3,BC=4,点D在边AC上,AD=AB,AE⊥BD,垂足为点F,交BC于点E,则BE的长为( )
A.2
B.
C.
D.
10.已知一直角三角形,三边的平方和为800cm2,则斜边长为( )
A.20cm
B.40cm
C.400cm
D.不能确定
二.填空题(共10小题,满分30分)
11.等腰三角形的腰长为,底长为2,则其腰上的高为
.
12.在△ABC中,AB=15,AC=20,D是BC边所在直线上的点,AD=12,BD=9,则BC=
.
13.三边为9,12,15的三角形,其面积为
.
14.如图所示,是一块由花园小道围成的边长为12米的正方形绿地,在离C处5米的绿地旁边B处有健身器材,为提醒居住在A处的居民爱护绿地,不直接穿过绿地从A到B,而是沿小道从A→C→B.小丽想在A处树立一个标牌“沿路多走■米,共建美丽家园”请问:小丽在标牌■填上的数字是
.
15.已知△ABC中,AB=k,AC=k﹣1,BC=3,当k=
时,∠C=90°.
16.如图,在△ABC中,BC=17,AB=8,AC=15,点D是BC中点,则AD的长为
.
17.古代著作《九章算术》中记载:今有池方一丈,葭生其中央,出水一尺.引葭赴岸,适与岸齐,水深几何?如图,其大意是:有一个边长为10尺的正方形池塘,一棵芦苇生长在它的正中央,高出水面1尺.如果把该芦苇拉向岸边,那么芦苇的顶部恰好碰到岸边,则水深
尺.
18.如图,秋千静止时,踏板离地的垂直高度BE=1m,将它往前推6m至C处时,水平距离CD=6m,踏板离地的垂直高度CF=4m,它的绳索始终拉直,则AC的长是m
.
19.在△ABC中,AB=15,AC=20,BC边上的高线为12,则△ABC的面积为
.
20.如图,甲、乙两艘客轮同时离开港口C,各自沿一固定方向航行,甲客轮每小时航行16nmile,乙客轮每小时航行12nmile,它们离开港口一个半小时后分别位于点A、B处,且相距30nmile.如果知道甲客轮沿着北偏西45°方向航行,则乙客轮的航行方向可能是
.
三.解答题(共6小题,满分60分)
21.如图,在一条东西走向河流的一侧有一村庄C,河边原有两个取水点A,B,其中AB=AC,由于某种原因,由C到A的路现在已经不通,该村为方便村民取水决定在河边新建一个取水点H(A、H、B在同一条直线上),并新建一条路CH,测得CB=1.5千米,CH=1.2千米,HB=0.9千米.
(1)问CH是否为从村庄C到河边的最近路?请通过计算加以说明;
(2)求新路CH比原路CA少多少千米?
22.如图,A,B两点相距14km,C、D为两村庄,DA⊥AB于A,CB⊥AB于B,已知DA=8km,CB=6km,现在要在AB上建一个供水站E,使得C、D两村到供水站E站的距离相等,则:
(1)E站应建在距A站多少千米处?
(2)DE和EC垂直吗?说明理由.
23.如图,将长为2.5米的梯子AB斜靠在墙AO上,BO长0.7米.如果将梯子的顶端A沿墙下滑0.4米,即AM等于0.4米,则梯脚B外移(即BN长)多少米?
24.如右图,一块四边形花圃ABCD中,已知∠B=90°,AB=4m,BC=3m,CD=12m,AD=13m.
(1)连接AC,判断△ACD的形状,并说明理由;
(2)求四边形花圃ABCD的面积.
25.如图,在荡秋千时,绳子最低点E离地面1m,荡到最高点D时离地面4m,此时水平位移BC是6m,求绳子长.
26.已知:如图,在Rt△ABC中,∠ACB=90°,AB=5cm,AC=3cm,动点P从点B出发沿射线BC以1cm/s的速度移动,设运动的时间为ts.
(1)求BC边的长;
(2)当△ABP为直角三角形时,求t的值.
参考答案
一.选择题(共10小题,满分30分)
1.解:过D作DE⊥AB于E,
在△ABC中,∠ACB=90°,BC=8cm,AC=6cm,
∴AB=10(cm),
∵,
∵AD平分∠BAC交BC于点D,DE⊥AB,∠ACB=90°,
∴DE=CD,
∴,
∴CD=3(cm),
∴BD=BC﹣DC=8﹣3=5(cm),
故选:C.
2.解:过点B作BC⊥AC,垂足为C.
观察图形可知AC=AF﹣MF+MC=8﹣3+1=6,BC=2+5=7,
在Rt△ACB中,AB=10(km).
答:登陆点到宝藏埋藏点的直线距离是10km,
故选:D.
3.解:由勾股定理得,AC2+BC2=AB2,
∴AC2=10﹣3=7,
∴S3=7,
故选:B.
4.解:A、22+32≠42,不符合勾股定理的逆定理,不能构成直角三角形,故本选项不符合题意;
B、42+52≠62,不符合勾股定理的逆定理,不能构成直角三角形,故本选项不符合题意;
C、32+42≠62,不符合勾股定理的逆定理,不能构成直角三角形,故本选项不符合题意;
D、62+82=102,符合勾股定理的逆定理,能构成直角三角形,故本选项符合题意.
故选:D.
5.解:如图,连接BD,
∵∠A=90°,AB=3cm,AD=4cm,
∴BD=5(cm),
∵BC=13cm,CD=12cm,52+122=132,
∴BD2+CD2=CB2,
∴∠BDC=90°,
∴S△DBC=×DB×CD=×5×12=30(cm2),
S△ABD=×3×4=6(cm2),
∴四边形ABCD的面积为30+6=36(cm2),
故选:D.
6.解:设每个小直角三角形的面积为m,则S1=4m+S2,S3=S2﹣4m,
∵S1+S2+S3=45,
∴4m+S2+S2+S2﹣4m=45,
即3S2=45,
解得S2=15.
故选:B.
7.解:如图,
m2+m2=(n﹣m)2,
2m2=n2﹣2mn+m2,
m2+2mn﹣n2=0.
故选:C.
8.解:
根据勾股定理得出:AB=5,
∴EF=AB=5,
∴阴影部分面积是EP2+PF2=25,
故选:B.
9.解:连接DE,
∵AD=AB,AE⊥BD,
∴AE是BD的垂直平分线,
∴DE=BE,
∴∠EBD=∠EDB,
∵AB=AD,
∴∠ABD=∠ADB,
∴∠ADE=∠ABE=90°,
在△ABC中,∠ABC=90°,
由勾股定理得:AC=5,
∴CD=AC﹣AD=5﹣3=2,
设BE=x,则CE=4﹣x,
在Rt△CDE中,由勾股定理得:
x2+22=(4﹣x)2,
解得x=,
∴BE=.
故选:B.
10.解:设直角三角形的两条直角边分别为acm、bcm,斜边为ccm.
根据题意,得a2+b2+c2=800,
∵a2+b2=c2,
∴2c2=800,
∴c2=400,
∵c>0,
∴C=200cm
故选:A.
二.填空题(共10小题,满分30分)
11.解:如图,△ABC中,AB=AC=,BC=2,
过点A作AD⊥BC,交BC于点D,
则BD=BC=1cm,
在Rt△ABD中,由勾股定理得AD,
设一腰上的高为h,
∵△ABC的面积=BC AD=AB h,
即1×= h,
解得h=.
故答案为.
12.解:如图1所示,当点D在线段BC上时,
∵AD=12,BD=9,AB=15,
∴AD2+BD2=AB2,
∴△ABD是直角三角形,且∠ADB=90°,
∴∠ADC=90°,
∴DC=16,
∴BC=BD+CD=9+16=25;
如图2所示,当点D在CB的延长线上时,
同理可得,DC=16,
∴BC=CD﹣BD=16﹣9=7;
由于AC>AB,所以点D不在BC的延长线上.
综上所述,BC的长度为25或7.
故答案为:25或7.
13.解:∵92+122=225=152,
∴三边长分别为9,12,15的三角形是直角三角形,
∴三角形的面积为:×9×12=54.
故答案为:54.
14.解:在Rt△ABC中,AB为斜边,
∴AB=13米,
少走的距离为
AC+BC﹣AB=(12+5)﹣13(米)=4米
答:小明在标牌■填上的数字是4.
故答案为:4.
15.解:∵∠C=90°,
∴AC2+BC2=AB2,
∵AB=k,AC=k﹣1,BC=3,
∴(k﹣1)2+32=k2,
解得:k=5,
故答案为:5.
16.解:∵△ABC中,AB=8,BC=17,AC=17,
∵152+82=172,即AC2+AB2=BC2,
∴△ABC是直角三角形,
∵点D是BC中点,
∴AD=,
故答案为:8.5.
17.解:依题意画出图形,
设芦苇长AB=AB′=x尺,则水深AC=(x﹣1)尺,
∵B′E=10尺,
∴B′C=5尺,
在Rt△AB′C中,52=(x﹣1)2=x2,
解之得x=13,
即水深12尺,
故答案为:12.
18.解:设秋千绳索AB的长度为xm,
由题意可得AC=AB=xm,
四边形DCFE为矩形,BE=1m,DC=6m,CF=4m,DE=CF=4m,
∴DB=DE﹣BE=3m,AD=AB﹣BD=(x﹣3)m,
在Rt△ADC中,AD2+DC2=AC2,
即(x﹣3)2+62=x2,
解得x=7.5,
即AC的长度为7.5m,
故答案为:7.5.
19.解:如图(1),△ABC中,AB=15,AC=20,BC边上高AD=12,
在Rt△ABD中AB=15,AD=12,
由勾股定理得,BD=9,
在Rt△ADC中AC=20,AD=12,
由勾股定理得,DC=16,
则BC的长为BD+DC=9+16=25,
△ABC的面积为:=150;
如图(2),
同(1)的作法相同,BC=7,
△ABC的面积为:=42,
故答案为:42或150.
20.解:AC的长度为:16×1.5=24(n
mile),
BC的长度为:12×1.5=18(n
mile),
∵302=242+182,
∴AB2=AC2+BC2,
∴△ABC是直角三角形,∠ACB=90°,
∵甲客轮沿着北偏西45°方向航行,
∴乙客轮的航行方向可能是北偏东45°,
故答案为:北偏东45°.
三.解答题(共6小题,满分60分)
21.解:(1)CH是从村庄C到河边的最近路.
理由如下:
∵CB=1.5千米,CH=1.2千米,HB=0.9千米,
∴CB2=CH2+HB2,
∴△BCH为直角三角形,∠BHC=90°,
∴CH⊥AB,
∴CH为C点到AB的最短路线;
(2)设AC=xkm,则AB=xkm,AH=(x﹣0.9)km,
在Rt△ACH中,(x﹣0.9)2+1.22=x2,
解得x=1.25,
即AC=1.25km,
∵AC﹣CH=1.25﹣1.2=0.05(km),
答:新路CH比原路CA少0.05千米.
22.解:(1)设AE=xkm,
∵C、D两村到E站的距离相等,∴DE=CE,即DE2=CE2,
由勾股定理,得82+x2=62+(14﹣x)2,
解得:x=6.
故E点应建在距A站6千米处;
(2)DE⊥CD,理由如下:
在Rt△DAE和Rt△CBE中,
,
∴Rt△DAE≌Rt△CBE(HL),
∴∠D=∠BEC,
∵∠D+∠AED=90°,
∴∠BEC+∠AED=90°,
∴∠DEC=90°,
∴DE⊥CD.
23.解:由题意得:AB=2.5米,BO=0.7米,
在Rt△ABO中,由勾股定理得:
AO=2.4(米),
∴MO=AO﹣AM=2.4﹣0.4=2(米),
在Rt△MNO中,由勾股定理得:
NO=1.5(米),
∴NB=ON﹣OB=1.5﹣0.7=0.8(米),
∴梯脚B外移(即BN长)0.8米.
24.解:(1)连接AC,
因为∠B=90°,所以直角△ABC中,由勾股定理得:
AC2=AB2+BC2,
AC2=42+32,
AC2=25,
∴AC=5m,又CD=12m,AD=13m,
所以△ACD中,AC2+CD2=AD2,
所以△ACD是直角三角形;
(2)S四边形ABCD=AC CD+AB BC
S四边形ABCD=×5×12+×4×3
=30+6
=36(m2),
答:该花圃的面积为36m2.
25.解:设绳子长为x米,
过D点作DF⊥AB于F,
根据题意得:AB=x+1(米),AF=x+1﹣4=x﹣3(米),
AD=x(米),DF=BC=6米,
由勾股定理得:(x﹣3)2+62=x2,
解得:x=7.5,
答:绳子长7.5米.
26.解:(1)在Rt△ABC中,由勾股定理得:BC=4(cm);
(2)由题意得:BP=tcm,分两种情况:
①当∠APB=90°时,如图1所示:
点P与点C重合,
∴BP=BC=4cm,
∴t=4;
②当∠BAP=90°时,如图2所示:
则CP=(t﹣4)cm,∠ACP=90°,
在Rt△ACP中,由勾股定理得:AP2=AC2+CP2,
在Rt△ABP中,由勾股定理得:AP2=BP2﹣AB2,
∴AC2+CP2=BP2﹣AB2,
即32+(t﹣4)2=t2﹣52,
解得:t=;
综上所述,当△ABP为直角三角形时,t的值为4s或s.
一.选择题(共10小题,满分30分)
1.如图,在△ABC中,∠ACB=90°,AD平分∠BAC交BC于点D,BC=8cm,AC=6cm,则BD的长为( )
A.3cm
B.4cm
C.5cm
D.6cm
2.国庆假期中,小华与同学去玩探宝游戏,按照探宝图,他们从门口A处出发先往东走8km,又往北走2km,遇到障碍后又往西走3km,再向北走到6km处往东拐,仅走了1km,就找到了宝藏,则门口A到藏宝点B的直线距离是( )
A.20km
B.14km
C.11km
D.10km
3.如图,在Rt△ABC中,∠ACB=90°,以△ABC的各边为边在△ABC外作三个正方形,S1,S2,S3分别表示这三个正方形的面积,若S1=3,S2=10,则S3=( )
A.5
B.7
C.13
D.15
4.下面四组线段中,可以构成直角三角形的是( )
A.2,3,4
B.4,5,6
C.3,4,6
D.6,8,10
5.如图,四边形ABCD中,AB=3cm,AD=4cm,BC=13cm,CD=12cm,且∠A=90°,则四边形ABCD的面积为( )
A.12cm2
B.18cm2
C.22cm2
D.36cm2
6.如图是由“赵爽弦图”变化得到的,它由八个全等的直角三角形拼接而成,记图中正方形ABCD,正方形EFGH,正方形MNPQ的面积分别为S1,S2,S3,若S1+S2+S3=45,则S2的值是( )
A.12
B.15
C.20
D.25
7.已知直角三角形纸片的两条直角边分别为m和n(m<n),过此三角形锐角的顶点把该纸片剪成两个三角形,若这两个三角形都为等腰三角形,则有( )
A.m2+2mn+n2=0
B.m2﹣2mn+n2=0
C.m2+2mn﹣n2=0
D.m2﹣2mn﹣n2=0
8.如图,由两个直角三角形和三个正方形组成的图形,大直角三角形的斜边和直角边长分别是13,12.则图中阴影部分的面积是( )
A.16
B.25
C.144
D.169
9.如图,在△ABC中,∠ABC=90°,AB=3,BC=4,点D在边AC上,AD=AB,AE⊥BD,垂足为点F,交BC于点E,则BE的长为( )
A.2
B.
C.
D.
10.已知一直角三角形,三边的平方和为800cm2,则斜边长为( )
A.20cm
B.40cm
C.400cm
D.不能确定
二.填空题(共10小题,满分30分)
11.等腰三角形的腰长为,底长为2,则其腰上的高为
.
12.在△ABC中,AB=15,AC=20,D是BC边所在直线上的点,AD=12,BD=9,则BC=
.
13.三边为9,12,15的三角形,其面积为
.
14.如图所示,是一块由花园小道围成的边长为12米的正方形绿地,在离C处5米的绿地旁边B处有健身器材,为提醒居住在A处的居民爱护绿地,不直接穿过绿地从A到B,而是沿小道从A→C→B.小丽想在A处树立一个标牌“沿路多走■米,共建美丽家园”请问:小丽在标牌■填上的数字是
.
15.已知△ABC中,AB=k,AC=k﹣1,BC=3,当k=
时,∠C=90°.
16.如图,在△ABC中,BC=17,AB=8,AC=15,点D是BC中点,则AD的长为
.
17.古代著作《九章算术》中记载:今有池方一丈,葭生其中央,出水一尺.引葭赴岸,适与岸齐,水深几何?如图,其大意是:有一个边长为10尺的正方形池塘,一棵芦苇生长在它的正中央,高出水面1尺.如果把该芦苇拉向岸边,那么芦苇的顶部恰好碰到岸边,则水深
尺.
18.如图,秋千静止时,踏板离地的垂直高度BE=1m,将它往前推6m至C处时,水平距离CD=6m,踏板离地的垂直高度CF=4m,它的绳索始终拉直,则AC的长是m
.
19.在△ABC中,AB=15,AC=20,BC边上的高线为12,则△ABC的面积为
.
20.如图,甲、乙两艘客轮同时离开港口C,各自沿一固定方向航行,甲客轮每小时航行16nmile,乙客轮每小时航行12nmile,它们离开港口一个半小时后分别位于点A、B处,且相距30nmile.如果知道甲客轮沿着北偏西45°方向航行,则乙客轮的航行方向可能是
.
三.解答题(共6小题,满分60分)
21.如图,在一条东西走向河流的一侧有一村庄C,河边原有两个取水点A,B,其中AB=AC,由于某种原因,由C到A的路现在已经不通,该村为方便村民取水决定在河边新建一个取水点H(A、H、B在同一条直线上),并新建一条路CH,测得CB=1.5千米,CH=1.2千米,HB=0.9千米.
(1)问CH是否为从村庄C到河边的最近路?请通过计算加以说明;
(2)求新路CH比原路CA少多少千米?
22.如图,A,B两点相距14km,C、D为两村庄,DA⊥AB于A,CB⊥AB于B,已知DA=8km,CB=6km,现在要在AB上建一个供水站E,使得C、D两村到供水站E站的距离相等,则:
(1)E站应建在距A站多少千米处?
(2)DE和EC垂直吗?说明理由.
23.如图,将长为2.5米的梯子AB斜靠在墙AO上,BO长0.7米.如果将梯子的顶端A沿墙下滑0.4米,即AM等于0.4米,则梯脚B外移(即BN长)多少米?
24.如右图,一块四边形花圃ABCD中,已知∠B=90°,AB=4m,BC=3m,CD=12m,AD=13m.
(1)连接AC,判断△ACD的形状,并说明理由;
(2)求四边形花圃ABCD的面积.
25.如图,在荡秋千时,绳子最低点E离地面1m,荡到最高点D时离地面4m,此时水平位移BC是6m,求绳子长.
26.已知:如图,在Rt△ABC中,∠ACB=90°,AB=5cm,AC=3cm,动点P从点B出发沿射线BC以1cm/s的速度移动,设运动的时间为ts.
(1)求BC边的长;
(2)当△ABP为直角三角形时,求t的值.
参考答案
一.选择题(共10小题,满分30分)
1.解:过D作DE⊥AB于E,
在△ABC中,∠ACB=90°,BC=8cm,AC=6cm,
∴AB=10(cm),
∵,
∵AD平分∠BAC交BC于点D,DE⊥AB,∠ACB=90°,
∴DE=CD,
∴,
∴CD=3(cm),
∴BD=BC﹣DC=8﹣3=5(cm),
故选:C.
2.解:过点B作BC⊥AC,垂足为C.
观察图形可知AC=AF﹣MF+MC=8﹣3+1=6,BC=2+5=7,
在Rt△ACB中,AB=10(km).
答:登陆点到宝藏埋藏点的直线距离是10km,
故选:D.
3.解:由勾股定理得,AC2+BC2=AB2,
∴AC2=10﹣3=7,
∴S3=7,
故选:B.
4.解:A、22+32≠42,不符合勾股定理的逆定理,不能构成直角三角形,故本选项不符合题意;
B、42+52≠62,不符合勾股定理的逆定理,不能构成直角三角形,故本选项不符合题意;
C、32+42≠62,不符合勾股定理的逆定理,不能构成直角三角形,故本选项不符合题意;
D、62+82=102,符合勾股定理的逆定理,能构成直角三角形,故本选项符合题意.
故选:D.
5.解:如图,连接BD,
∵∠A=90°,AB=3cm,AD=4cm,
∴BD=5(cm),
∵BC=13cm,CD=12cm,52+122=132,
∴BD2+CD2=CB2,
∴∠BDC=90°,
∴S△DBC=×DB×CD=×5×12=30(cm2),
S△ABD=×3×4=6(cm2),
∴四边形ABCD的面积为30+6=36(cm2),
故选:D.
6.解:设每个小直角三角形的面积为m,则S1=4m+S2,S3=S2﹣4m,
∵S1+S2+S3=45,
∴4m+S2+S2+S2﹣4m=45,
即3S2=45,
解得S2=15.
故选:B.
7.解:如图,
m2+m2=(n﹣m)2,
2m2=n2﹣2mn+m2,
m2+2mn﹣n2=0.
故选:C.
8.解:
根据勾股定理得出:AB=5,
∴EF=AB=5,
∴阴影部分面积是EP2+PF2=25,
故选:B.
9.解:连接DE,
∵AD=AB,AE⊥BD,
∴AE是BD的垂直平分线,
∴DE=BE,
∴∠EBD=∠EDB,
∵AB=AD,
∴∠ABD=∠ADB,
∴∠ADE=∠ABE=90°,
在△ABC中,∠ABC=90°,
由勾股定理得:AC=5,
∴CD=AC﹣AD=5﹣3=2,
设BE=x,则CE=4﹣x,
在Rt△CDE中,由勾股定理得:
x2+22=(4﹣x)2,
解得x=,
∴BE=.
故选:B.
10.解:设直角三角形的两条直角边分别为acm、bcm,斜边为ccm.
根据题意,得a2+b2+c2=800,
∵a2+b2=c2,
∴2c2=800,
∴c2=400,
∵c>0,
∴C=200cm
故选:A.
二.填空题(共10小题,满分30分)
11.解:如图,△ABC中,AB=AC=,BC=2,
过点A作AD⊥BC,交BC于点D,
则BD=BC=1cm,
在Rt△ABD中,由勾股定理得AD,
设一腰上的高为h,
∵△ABC的面积=BC AD=AB h,
即1×= h,
解得h=.
故答案为.
12.解:如图1所示,当点D在线段BC上时,
∵AD=12,BD=9,AB=15,
∴AD2+BD2=AB2,
∴△ABD是直角三角形,且∠ADB=90°,
∴∠ADC=90°,
∴DC=16,
∴BC=BD+CD=9+16=25;
如图2所示,当点D在CB的延长线上时,
同理可得,DC=16,
∴BC=CD﹣BD=16﹣9=7;
由于AC>AB,所以点D不在BC的延长线上.
综上所述,BC的长度为25或7.
故答案为:25或7.
13.解:∵92+122=225=152,
∴三边长分别为9,12,15的三角形是直角三角形,
∴三角形的面积为:×9×12=54.
故答案为:54.
14.解:在Rt△ABC中,AB为斜边,
∴AB=13米,
少走的距离为
AC+BC﹣AB=(12+5)﹣13(米)=4米
答:小明在标牌■填上的数字是4.
故答案为:4.
15.解:∵∠C=90°,
∴AC2+BC2=AB2,
∵AB=k,AC=k﹣1,BC=3,
∴(k﹣1)2+32=k2,
解得:k=5,
故答案为:5.
16.解:∵△ABC中,AB=8,BC=17,AC=17,
∵152+82=172,即AC2+AB2=BC2,
∴△ABC是直角三角形,
∵点D是BC中点,
∴AD=,
故答案为:8.5.
17.解:依题意画出图形,
设芦苇长AB=AB′=x尺,则水深AC=(x﹣1)尺,
∵B′E=10尺,
∴B′C=5尺,
在Rt△AB′C中,52=(x﹣1)2=x2,
解之得x=13,
即水深12尺,
故答案为:12.
18.解:设秋千绳索AB的长度为xm,
由题意可得AC=AB=xm,
四边形DCFE为矩形,BE=1m,DC=6m,CF=4m,DE=CF=4m,
∴DB=DE﹣BE=3m,AD=AB﹣BD=(x﹣3)m,
在Rt△ADC中,AD2+DC2=AC2,
即(x﹣3)2+62=x2,
解得x=7.5,
即AC的长度为7.5m,
故答案为:7.5.
19.解:如图(1),△ABC中,AB=15,AC=20,BC边上高AD=12,
在Rt△ABD中AB=15,AD=12,
由勾股定理得,BD=9,
在Rt△ADC中AC=20,AD=12,
由勾股定理得,DC=16,
则BC的长为BD+DC=9+16=25,
△ABC的面积为:=150;
如图(2),
同(1)的作法相同,BC=7,
△ABC的面积为:=42,
故答案为:42或150.
20.解:AC的长度为:16×1.5=24(n
mile),
BC的长度为:12×1.5=18(n
mile),
∵302=242+182,
∴AB2=AC2+BC2,
∴△ABC是直角三角形,∠ACB=90°,
∵甲客轮沿着北偏西45°方向航行,
∴乙客轮的航行方向可能是北偏东45°,
故答案为:北偏东45°.
三.解答题(共6小题,满分60分)
21.解:(1)CH是从村庄C到河边的最近路.
理由如下:
∵CB=1.5千米,CH=1.2千米,HB=0.9千米,
∴CB2=CH2+HB2,
∴△BCH为直角三角形,∠BHC=90°,
∴CH⊥AB,
∴CH为C点到AB的最短路线;
(2)设AC=xkm,则AB=xkm,AH=(x﹣0.9)km,
在Rt△ACH中,(x﹣0.9)2+1.22=x2,
解得x=1.25,
即AC=1.25km,
∵AC﹣CH=1.25﹣1.2=0.05(km),
答:新路CH比原路CA少0.05千米.
22.解:(1)设AE=xkm,
∵C、D两村到E站的距离相等,∴DE=CE,即DE2=CE2,
由勾股定理,得82+x2=62+(14﹣x)2,
解得:x=6.
故E点应建在距A站6千米处;
(2)DE⊥CD,理由如下:
在Rt△DAE和Rt△CBE中,
,
∴Rt△DAE≌Rt△CBE(HL),
∴∠D=∠BEC,
∵∠D+∠AED=90°,
∴∠BEC+∠AED=90°,
∴∠DEC=90°,
∴DE⊥CD.
23.解:由题意得:AB=2.5米,BO=0.7米,
在Rt△ABO中,由勾股定理得:
AO=2.4(米),
∴MO=AO﹣AM=2.4﹣0.4=2(米),
在Rt△MNO中,由勾股定理得:
NO=1.5(米),
∴NB=ON﹣OB=1.5﹣0.7=0.8(米),
∴梯脚B外移(即BN长)0.8米.
24.解:(1)连接AC,
因为∠B=90°,所以直角△ABC中,由勾股定理得:
AC2=AB2+BC2,
AC2=42+32,
AC2=25,
∴AC=5m,又CD=12m,AD=13m,
所以△ACD中,AC2+CD2=AD2,
所以△ACD是直角三角形;
(2)S四边形ABCD=AC CD+AB BC
S四边形ABCD=×5×12+×4×3
=30+6
=36(m2),
答:该花圃的面积为36m2.
25.解:设绳子长为x米,
过D点作DF⊥AB于F,
根据题意得:AB=x+1(米),AF=x+1﹣4=x﹣3(米),
AD=x(米),DF=BC=6米,
由勾股定理得:(x﹣3)2+62=x2,
解得:x=7.5,
答:绳子长7.5米.
26.解:(1)在Rt△ABC中,由勾股定理得:BC=4(cm);
(2)由题意得:BP=tcm,分两种情况:
①当∠APB=90°时,如图1所示:
点P与点C重合,
∴BP=BC=4cm,
∴t=4;
②当∠BAP=90°时,如图2所示:
则CP=(t﹣4)cm,∠ACP=90°,
在Rt△ACP中,由勾股定理得:AP2=AC2+CP2,
在Rt△ABP中,由勾股定理得:AP2=BP2﹣AB2,
∴AC2+CP2=BP2﹣AB2,
即32+(t﹣4)2=t2﹣52,
解得:t=;
综上所述,当△ABP为直角三角形时,t的值为4s或s.
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
