人教九上数学21.3 用一元二次方程解决常见实际问题总结课件(44张ppt)
文档属性
| 名称 | 人教九上数学21.3 用一元二次方程解决常见实际问题总结课件(44张ppt) |  | |
| 格式 | ppt | ||
| 文件大小 | 568.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-03 16:42:05 | ||
图片预览










文档简介
(共45张PPT)
用一元二次方程解决常见实际问题
总
结
【常见类型】
列一元二次方程解决实际问题的常见类型有以下几种
(1)增长率问题
(2)几何中面积、长度问题
(3)假设存在问题
(4)排列组合问题
(5)销售问题
(一)增长率问题
例1
某市为了解决市民看病难的问题,决定下调药品的价格.某种药品经过连续两次降价后,由每盒200元下调至128元,求这种药品平均每次降价的百分率是多少?
小结
1.
列一元二次方程解应用题的一般步骤与列一元一次方程解应用题一样,所以列一元二次方程解应用题的一般步骤也归纳为:审、设、列、解、检验、答这六个步骤.
(1)审:是指读懂题目,弄清题意,明确哪些是已知量,哪些是未知量以及它们之间的等量关系;
(2)设:是指设元,也就是设未知数;
(3)列:就是列方程,这是非常重要的关键步骤,一般先找出能够表达应用题全部含义的一个相等关系,然后列代数式表示相等关系中的各个量,就得到含有未知数的等式,即方程;
(5)检验:列方程解应用题时,要对所求出的未知数进行检验,检验的目的有两个:其一,检验求出来的未知数的值是否满足方程;其二,检验求出的未知数的值是不是满足实际问题的要求,对于适合方程而不适合实际问题的未知数的值应舍去;
(4)解:就是解方程,求出未知数的值;
(6)答:就是写出答案,其中在书写时还要注意不要漏写单位名称.
2.对于“增长率”问题,如人口的减少、利率的降低、汽车的折旧等等,都是在原来基数上减少,不能与一般性的增加和减少相混淆.
例如
课本探究2
上次试题第二章填空题
某企业为节约用水
练习
植树造林,某中学师生从2006年到2009年四年内共植树1999棵,已知该校2006年植树344棵,2007年植树500棵,如果从2007年到2009年的指数棵树的年平均增长率相同,那么该校2009年植树棵树多少颗?
344+500+500(1+X)+500(1+X)2
解得x=0.1
x=-3(不合题意舍去)
总结
平均增长率问题中的基本数量关系为
A(1+X)n=B(A为始量,B为终止量,n为增长的次数,x为平均增长率)
类似的还有平均降低率问题中的基本数量关系为A(1-X)n=B(A为始量,B为终止量,n为降低的次数,x为平均降低率)
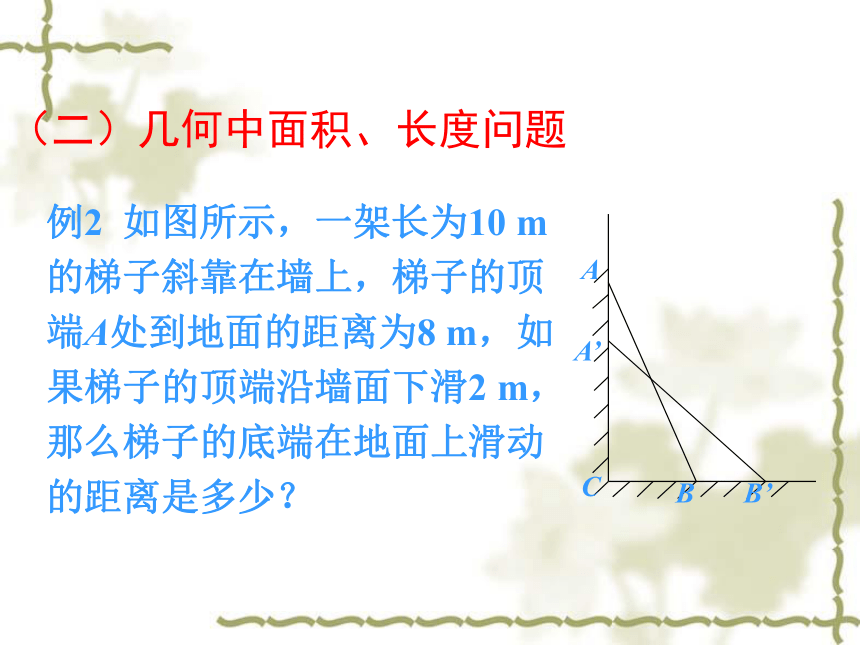
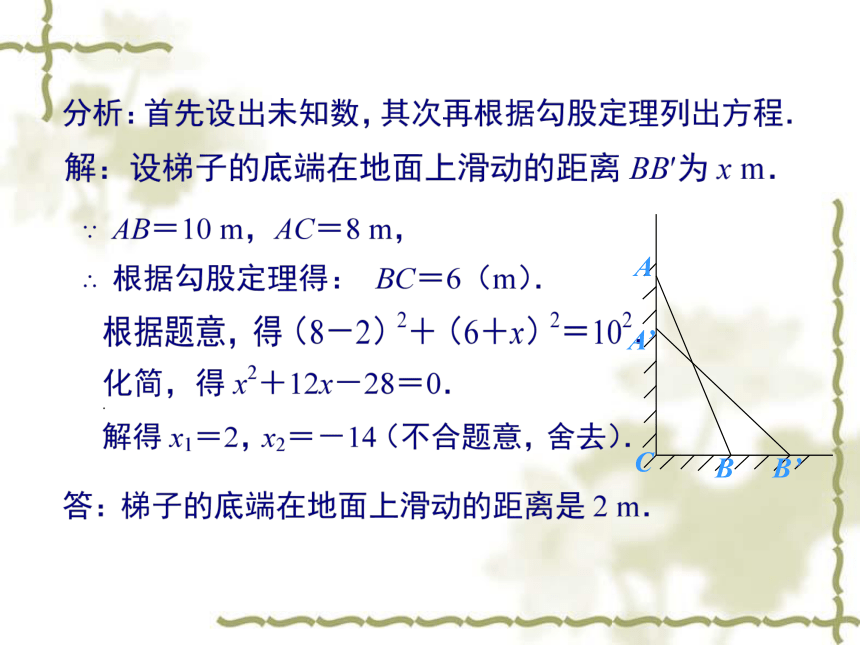
例2
如图所示,一架长为10
m的梯子斜靠在墙上,梯子的顶端A处到地面的距离为8
m,如果梯子的顶端沿墙面下滑2
m,那么梯子的底端在地面上滑动的距离是多少?
A
A’
C
B
B’
(二)几何中面积、长度问题
A
A’
C
B
B’
小结
1.解法二和解法一相比更简单,它利用“图形经过移动,它的面积大小不会改变”的道理,把纵、横两条路移动一下,可以使列方程容易些(目的是求出路面的宽,至于实际施工,仍可按原图的位置修路).
2.有些同学在列方程解应用题时,往往看到正解就保留,看到负解就舍去.其实,即使是正解也要根据题设条件进行检验,该舍就舍.此题一定要注意原矩形“宽为20
m、长为32
m”这个条件,从而进行正确取舍.
总结
解决此类问题
必须具备良好的几何概念知识,熟悉长度,面积,体积等公式。
有时需要通过平移的方法来解决问题。
常见问题:挖沟的宽度,制作盒子,例如课本探究3
设计书的封面
练习
有一个面积为150m2的长方形鸡场,鸡场的一边靠墙(墙长18米),另一边用篱笆围成,如果篱笆的长为35米,求鸡场的长与宽各是多少?
长为15米
宽为10米
小结
例如
上次测试题
用22厘米长的铁丝围成面积为31平方厘米的矩形。
练习
用长为100米的金属制成一个长方形框,框的面积为下列数据时,求矿的各边长。
1.
576平方米
2.
625平方米
3.
700平方米
答案
1.
长为32米
宽为18米
2.
长宽都是25米
3.
不能制成700平方米的框
总结
列出方程后根据判别式看是否有解,无解说明不能完成。等于零说明正方形。
一定要确定长宽各是多少,长大于宽,宽大于长则舍去。
例5
在一次聚会中,每两个参加聚会的人都相互握了一次手,一共握了45次手,问参加这次聚会的人数是多少?
(四)排列组合问题
例如
课本一元二次方程问题二要组织一次排球邀请赛,比赛者应该邀请独傲少个队参赛。
练习
某旅行团结束旅行,其中建议大家互相告别,细心的小明发现,每两个参加旅行的人相互握手一次,共握手66次,问这次旅行的人有多少?
例6
某商场销售一批名牌衬衫,平均每天可销售出20件,每件盈利40元,经调查发现,如果每件衬衫每降价1元,商场平均每天可多售出2件.若商场平均每天要盈利1200元,每件衬衫应降价多少元?
(五)销售问题
分析:这类销售问题,涉及的数量关系比较多,我们可以通过列表的方式来分析其中的数量关系.
每天的销售量(件)
每件衬衫的盈利(元)
总利润(元)
降价前
降价后
20
40
800
20+2x
40-x
1200
例7
(2010南京)某批发商以每件50元的价格购进800件T恤.第一个月以单价80元销售,售出了200件;第二个月如果单价不变,预计仍可售出200件,批发商为增加销售量,决定降价销售,根据市场调查,单价每降低1元,可多售出10件,但最低单价应高于购进的价格;第二个月结束后,批发商将对剩余的T恤一性清仓,清仓时单价为40元.设第二个月单价降低x元.
(1)填表(不需化简):
时间
第一个月
第二个月
清仓
单价(元)
80
40
销售量(件)
200
(2)如果批发商希望通过销售这批T恤获利9000元,那么第二个月的单价应是多少元?
分析:
时间
第一个月
第二个月
清仓
单价(元)
80
40
销售量(件)
200
800-200-(200+10x)
80-x
200+10x
1.列方程解实际问题,一般分为审题、设未知数、列方程、解方程、检验、写出答案这六步进行,其中审题过程虽在草稿纸上进行,但这一步非常重要,只有经过认真审题,分清已知条件和所求量,明确量与量之间的数量关系,才能准确找出相等关系,列出方程.
【方法总结】
2.在列一元二次方程解实际问题时还要注意一些关键的词语,如“多”、“倍”、“差”、“提前”、“同时”、“早到”、“迟到”、“增加几倍”等.
3.在解决复杂问题时,我们可以借助于列表格等辅助方式弄清题目中的数量关系,列出方程.
4.一元二次方程是我们日常生活中解决许多问题的有效模型,我们要善于利用列一元二次方程求解这个数学模型解决实际生活中的各种问题,并注意要根据实际意义进行解释和检验,从中体会数学建模的思想方法.
用一元二次方程解决常见实际问题
总
结
【常见类型】
列一元二次方程解决实际问题的常见类型有以下几种
(1)增长率问题
(2)几何中面积、长度问题
(3)假设存在问题
(4)排列组合问题
(5)销售问题
(一)增长率问题
例1
某市为了解决市民看病难的问题,决定下调药品的价格.某种药品经过连续两次降价后,由每盒200元下调至128元,求这种药品平均每次降价的百分率是多少?
小结
1.
列一元二次方程解应用题的一般步骤与列一元一次方程解应用题一样,所以列一元二次方程解应用题的一般步骤也归纳为:审、设、列、解、检验、答这六个步骤.
(1)审:是指读懂题目,弄清题意,明确哪些是已知量,哪些是未知量以及它们之间的等量关系;
(2)设:是指设元,也就是设未知数;
(3)列:就是列方程,这是非常重要的关键步骤,一般先找出能够表达应用题全部含义的一个相等关系,然后列代数式表示相等关系中的各个量,就得到含有未知数的等式,即方程;
(5)检验:列方程解应用题时,要对所求出的未知数进行检验,检验的目的有两个:其一,检验求出来的未知数的值是否满足方程;其二,检验求出的未知数的值是不是满足实际问题的要求,对于适合方程而不适合实际问题的未知数的值应舍去;
(4)解:就是解方程,求出未知数的值;
(6)答:就是写出答案,其中在书写时还要注意不要漏写单位名称.
2.对于“增长率”问题,如人口的减少、利率的降低、汽车的折旧等等,都是在原来基数上减少,不能与一般性的增加和减少相混淆.
例如
课本探究2
上次试题第二章填空题
某企业为节约用水
练习
植树造林,某中学师生从2006年到2009年四年内共植树1999棵,已知该校2006年植树344棵,2007年植树500棵,如果从2007年到2009年的指数棵树的年平均增长率相同,那么该校2009年植树棵树多少颗?
344+500+500(1+X)+500(1+X)2
解得x=0.1
x=-3(不合题意舍去)
总结
平均增长率问题中的基本数量关系为
A(1+X)n=B(A为始量,B为终止量,n为增长的次数,x为平均增长率)
类似的还有平均降低率问题中的基本数量关系为A(1-X)n=B(A为始量,B为终止量,n为降低的次数,x为平均降低率)
例2
如图所示,一架长为10
m的梯子斜靠在墙上,梯子的顶端A处到地面的距离为8
m,如果梯子的顶端沿墙面下滑2
m,那么梯子的底端在地面上滑动的距离是多少?
A
A’
C
B
B’
(二)几何中面积、长度问题
A
A’
C
B
B’
小结
1.解法二和解法一相比更简单,它利用“图形经过移动,它的面积大小不会改变”的道理,把纵、横两条路移动一下,可以使列方程容易些(目的是求出路面的宽,至于实际施工,仍可按原图的位置修路).
2.有些同学在列方程解应用题时,往往看到正解就保留,看到负解就舍去.其实,即使是正解也要根据题设条件进行检验,该舍就舍.此题一定要注意原矩形“宽为20
m、长为32
m”这个条件,从而进行正确取舍.
总结
解决此类问题
必须具备良好的几何概念知识,熟悉长度,面积,体积等公式。
有时需要通过平移的方法来解决问题。
常见问题:挖沟的宽度,制作盒子,例如课本探究3
设计书的封面
练习
有一个面积为150m2的长方形鸡场,鸡场的一边靠墙(墙长18米),另一边用篱笆围成,如果篱笆的长为35米,求鸡场的长与宽各是多少?
长为15米
宽为10米
小结
例如
上次测试题
用22厘米长的铁丝围成面积为31平方厘米的矩形。
练习
用长为100米的金属制成一个长方形框,框的面积为下列数据时,求矿的各边长。
1.
576平方米
2.
625平方米
3.
700平方米
答案
1.
长为32米
宽为18米
2.
长宽都是25米
3.
不能制成700平方米的框
总结
列出方程后根据判别式看是否有解,无解说明不能完成。等于零说明正方形。
一定要确定长宽各是多少,长大于宽,宽大于长则舍去。
例5
在一次聚会中,每两个参加聚会的人都相互握了一次手,一共握了45次手,问参加这次聚会的人数是多少?
(四)排列组合问题
例如
课本一元二次方程问题二要组织一次排球邀请赛,比赛者应该邀请独傲少个队参赛。
练习
某旅行团结束旅行,其中建议大家互相告别,细心的小明发现,每两个参加旅行的人相互握手一次,共握手66次,问这次旅行的人有多少?
例6
某商场销售一批名牌衬衫,平均每天可销售出20件,每件盈利40元,经调查发现,如果每件衬衫每降价1元,商场平均每天可多售出2件.若商场平均每天要盈利1200元,每件衬衫应降价多少元?
(五)销售问题
分析:这类销售问题,涉及的数量关系比较多,我们可以通过列表的方式来分析其中的数量关系.
每天的销售量(件)
每件衬衫的盈利(元)
总利润(元)
降价前
降价后
20
40
800
20+2x
40-x
1200
例7
(2010南京)某批发商以每件50元的价格购进800件T恤.第一个月以单价80元销售,售出了200件;第二个月如果单价不变,预计仍可售出200件,批发商为增加销售量,决定降价销售,根据市场调查,单价每降低1元,可多售出10件,但最低单价应高于购进的价格;第二个月结束后,批发商将对剩余的T恤一性清仓,清仓时单价为40元.设第二个月单价降低x元.
(1)填表(不需化简):
时间
第一个月
第二个月
清仓
单价(元)
80
40
销售量(件)
200
(2)如果批发商希望通过销售这批T恤获利9000元,那么第二个月的单价应是多少元?
分析:
时间
第一个月
第二个月
清仓
单价(元)
80
40
销售量(件)
200
800-200-(200+10x)
80-x
200+10x
1.列方程解实际问题,一般分为审题、设未知数、列方程、解方程、检验、写出答案这六步进行,其中审题过程虽在草稿纸上进行,但这一步非常重要,只有经过认真审题,分清已知条件和所求量,明确量与量之间的数量关系,才能准确找出相等关系,列出方程.
【方法总结】
2.在列一元二次方程解实际问题时还要注意一些关键的词语,如“多”、“倍”、“差”、“提前”、“同时”、“早到”、“迟到”、“增加几倍”等.
3.在解决复杂问题时,我们可以借助于列表格等辅助方式弄清题目中的数量关系,列出方程.
4.一元二次方程是我们日常生活中解决许多问题的有效模型,我们要善于利用列一元二次方程求解这个数学模型解决实际生活中的各种问题,并注意要根据实际意义进行解释和检验,从中体会数学建模的思想方法.
同课章节目录
