2021年新教材高中数学1.2空间向量基本定理(word 含解析)
文档属性
| 名称 | 2021年新教材高中数学1.2空间向量基本定理(word 含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 524.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-09 00:00:00 | ||
图片预览



文档简介
空间向量基本定理
基础练 (15分钟 30分)
1.已知边长为1的正方体ABCD A1B1C1D1的上底面A1B1C1D1的中心为O1,则·的值为( )
A.-1
B.0
C.1
D.2
2.若{e1,e2,e3}是空间向量的一个基底,又a=e1+e2+e3,b=e1+e2-e3,c=e1-e2+e3,d=e1+2e2+3e3,d=xa+yb+zc,则x,y,z的值分别为( )
A.,-1,-
B.-1,,-
C.,1,
D.-,1,
3.已知a,b是异面直线,A,B∈a,C,D∈b,AC⊥b,BD⊥b,且AB=2,CD=1,则a,b所成的角是________.
4.{a,b,c}为空间的一个基底,且存在实数x,y,z使得xa+yb+zc=0,则x=________,y=________,z=________.
5.如图,四棱锥P OABC的底面为一矩形,PO⊥平面OABC,设=a,=b,=c,E,F分别是PC和PB的中点,用a,b,c表示,,,.
能力练(30分钟 60分)
一、单选题(每小题5分,共20分)
1.O,A,B,C为空间四点,且向量,,不能构成空间的一个基底,则( )
A.,,共线
B.,共线
C.,共线
D.O,A,B,C四点共面
2.在长方体ABCD A1B1C1D1中,AC与BD的交点为M,设=a,=b,=c,则下列向量中与相等的向量是
( )
A.-a+b+c
B.a+b+c
C.a-b+c
D.-a-b+c
3.已知在空间四边形ABCD中,∠ACD=∠BDC=90°,且AB=2,CD=1,则AB与CD所成的角是( )
A.30°
B.45°
C.60°
D.90°
4.点P是矩形ABCD所在平面外一点,且PA⊥平面ABCD,M,N分别是PC,PD上的点,且=,=,则满足=x+y+z的实数x,y,z的值分别为( )
A.-,,
B.,-,
C.-,,-
D.-,-,
二、多选题(每小题5分,共10分,全部选对得5分,选对但不全的得3分,有选错的得0分)
5.下列说法正确的是( )
A.若两个非零向量a,b与任何一个向量都不能构成空间的一个基底,则a,b共线
B.空间的基底有且仅有一个
C.两两垂直的三个非零向量可以构成空间的一个基底
D.基底{a,b,c}中基向量与基底{e,f,g}中基向量对应相等
6.已知在空间四面体O ABC中,点M在线段OA上,且OM=2MA,点N为BC中点,设=a,=b,=c,则( )
A.=a+b-c
B.=-a+b+c
C.=a-c
D.=a+b-c
三、填空题(每小题5分,共10分)
7.在空间中平移△ABC到△A1B1C1(使△A1B1C1与△ABC不共面),连接对应顶点.设=a,=b,=c,M是BC1的中点,N是B1C1的中点,用基底{a,b,c}表示向量+的结果为________.
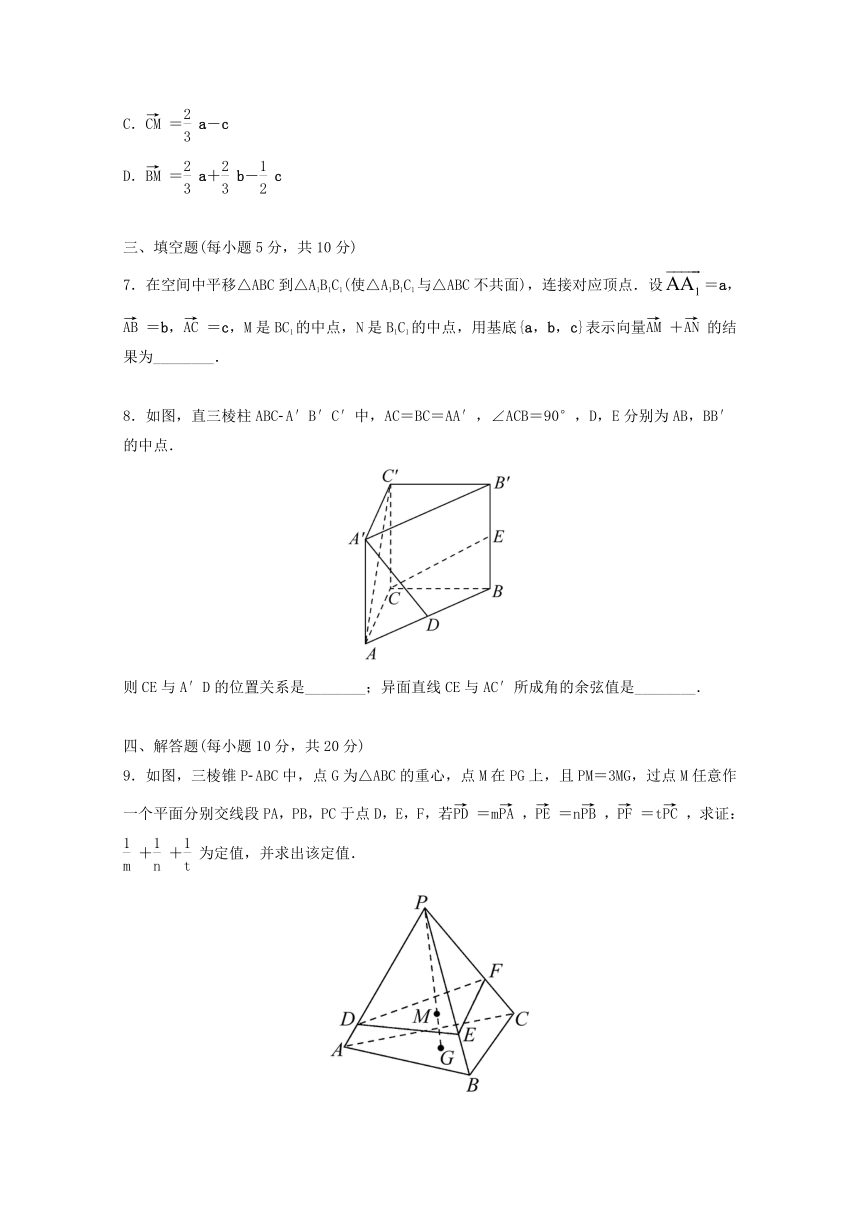
8.如图,直三棱柱ABC A′B′C′中,AC=BC=AA′,∠ACB=90°,D,E分别为AB,BB′的中点.
则CE与A′D的位置关系是________;异面直线CE与AC′所成角的余弦值是________.
四、解答题(每小题10分,共20分)
9.如图,三棱锥P ABC中,点G为△ABC的重心,点M在PG上,且PM=3MG,过点M任意作一个平面分别交线段PA,PB,PC于点D,E,F,若=m,=n,=t,求证:++为定值,并求出该定值.
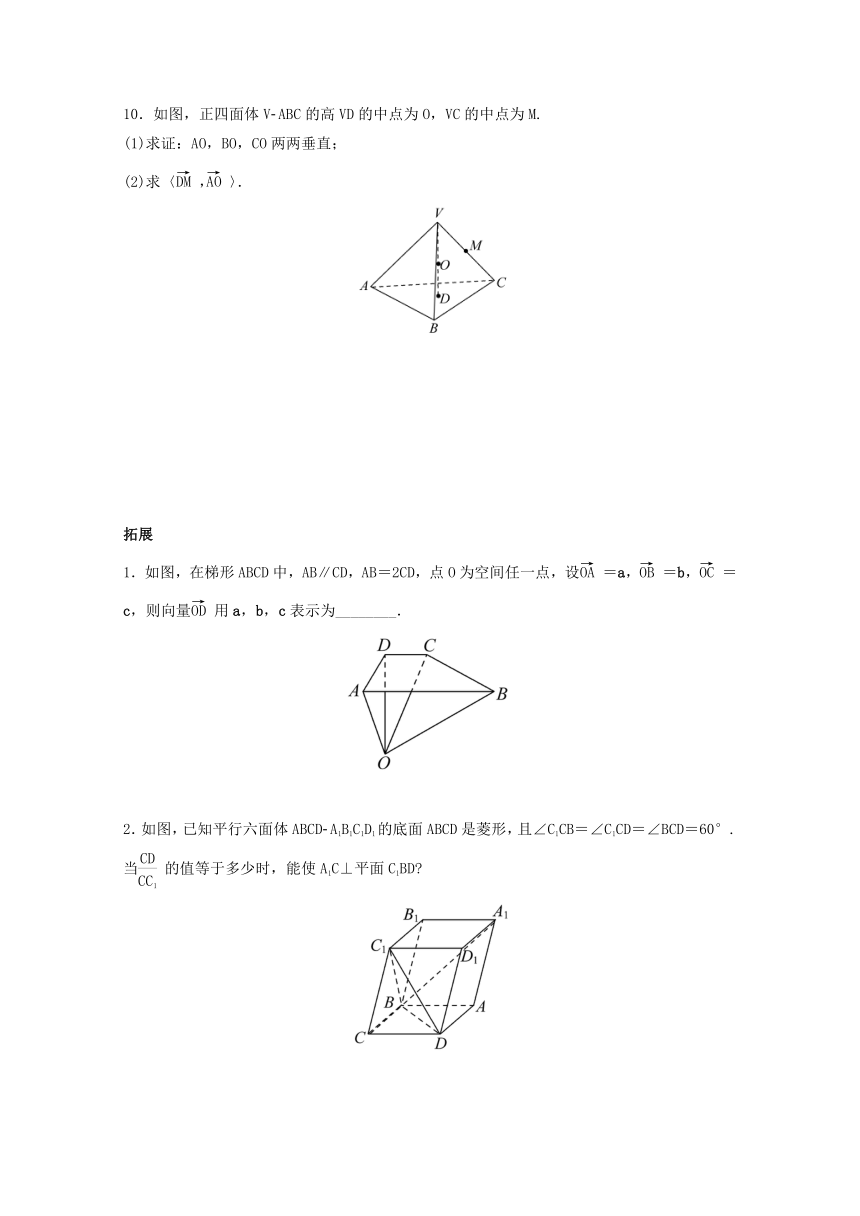
10.如图,正四面体V ABC的高VD的中点为O,VC的中点为M.
(1)求证:AO,BO,CO两两垂直;
(2)求〈,〉.
拓展
1.如图,在梯形ABCD中,AB∥CD,AB=2CD,点O为空间任一点,设=a,=b,=c,则向量用a,b,c表示为________.
2.如图,已知平行六面体ABCD A1B1C1D1的底面ABCD是菱形,且∠C1CB=∠C1CD=∠BCD=60°.当的值等于多少时,能使A1C⊥平面C1BD
参考答案:
基础练 (15分钟 30分)
1.已知边长为1的正方体ABCD A1B1C1D1的上底面A1B1C1D1的中心为O1,则·的值为( )
A.-1
B.0
C.1
D.2
【解析】选C.==+=+(+),而=+,
则·=(2+2)=1.
2.若{e1,e2,e3}是空间向量的一个基底,又a=e1+e2+e3,b=e1+e2-e3,c=e1-e2+e3,d=e1+2e2+3e3,d=xa+yb+zc,则x,y,z的值分别为( )
A.,-1,-
B.-1,,-
C.,1,
D.-,1,
【解析】选A.由题意得,d=xa+yb+zc=x(e1+e2+e3)+y(e1+e2-e3)+z(e1-e2+e3)=(x+y+z)e1+(x+y-z)e2+(x-y+z)e3=e1+2e2+3e3,由空间向量基本定理,得解得
3.已知a,b是异面直线,A,B∈a,C,D∈b,AC⊥b,BD⊥b,且AB=2,CD=1,则a,b所成的角是________.
【解析】=++,
所以·=·(++)=||2=1,
所以cos
〈,〉==,
所以异面直线a,b所成的角是60°.
答案:60°
4.{a,b,c}为空间的一个基底,且存在实数x,y,z使得xa+yb+zc=0,则x=________,y=________,z=________.
【解析】若x,y,z中存在一个不为0的数,不妨设x≠0,则a=-b-c,所以a,b,c共面.这与{a,b,c}是基底矛盾,故x=y=z=0.
答案:0 0 0
5.如图,四棱锥P OABC的底面为一矩形,PO⊥平面OABC,设=a,=b,=c,E,F分别是PC和PB的中点,用a,b,c表示,,,.
【解析】==-=-(+)=-a-b+c;
=-=(+)-(+)
=--+=-a-b+c;
=-=(+)-
=-a+b+c;
===a.
能力练(30分钟 60分)
一、单选题(每小题5分,共20分)
1.O,A,B,C为空间四点,且向量,,不能构成空间的一个基底,则( )
A.,,共线
B.,共线
C.,共线
D.O,A,B,C四点共面
【解析】选D.由题意知,向量,,共面,从而O,A,B,C四点共面.
2.在长方体ABCD A1B1C1D1中,AC与BD的交点为M,设=a,=b,=c,则下列向量中与相等的向量是
( )
A.-a+b+c
B.a+b+c
C.a-b+c
D.-a-b+c
【解析】选A.=+
=+=+(+)
=+=c+(-a+b)
=-a+b+c.
3.已知在空间四边形ABCD中,∠ACD=∠BDC=90°,且AB=2,CD=1,则AB与CD所成的角是( )
A.30°
B.45°
C.60°
D.90°
【解析】选C.由题意得·=·=0,
所以·=(++)·=·+
||2+·=||2=1,所以cos
〈,〉==,所以AB与CD所成的角为60°.
4.点P是矩形ABCD所在平面外一点,且PA⊥平面ABCD,M,N分别是PC,PD上的点,且=,=,则满足=x+y+z的实数x,y,z的值分别为( )
A.-,,
B.,-,
C.-,,-
D.-,-,
【解析】选D.如图所示,取PC的中点E,连接NE,
则=-=-(-)
=-=-
=--(-++)=--+,又=x+y+z,则x=-,y=-,z=.
二、多选题(每小题5分,共10分,全部选对得5分,选对但不全的得3分,有选错的得0分)
5.下列说法正确的是( )
A.若两个非零向量a,b与任何一个向量都不能构成空间的一个基底,则a,b共线
B.空间的基底有且仅有一个
C.两两垂直的三个非零向量可以构成空间的一个基底
D.基底{a,b,c}中基向量与基底{e,f,g}中基向量对应相等
【解析】选AC.A项中若a,b不共线,则任意与a,b不共面的向量就可以和a,b构成空间的一个基底,A对;B项中空间基底有无数个,B错;C项显然正确;D项中因为基底不唯一,所以D错.
6.已知在空间四面体O ABC中,点M在线段OA上,且OM=2MA,点N为BC中点,设=a,=b,=c,则( )
A.=a+b-c
B.=-a+b+c
C.=a-c
D.=a+b-c
【解析】选BC.=(+)=c+b-a;=-=(+)-=b+c-a;
=+=-c+a;=+=a-b.
三、填空题(每小题5分,共10分)
7.在空间中平移△ABC到△A1B1C1(使△A1B1C1与△ABC不共面),连接对应顶点.设=a,=b,=c,M是BC1的中点,N是B1C1的中点,用基底{a,b,c}表示向量+的结果为________.
【解析】如图,
+=(+)+
=+=b+(a+b)+(a+c)
=a+b+c.
答案:a+b+c
8.如图,直三棱柱ABC A′B′C′中,AC=BC=AA′,∠ACB=90°,D,E分别为AB,BB′的中点.
则CE与A′D的位置关系是________;异面直线CE与AC′所成角的余弦值是________.
【解析】设=a,=b,=c,
根据题意,|a|=|b|=|c|且a·b=b·c=c·a=0,所以=b+c,=-c+b-a.所以·=-c2+b2=0.所以⊥,即CE与
A′D垂直;因为=-a+c,所以||=|a|.又||=|a|,·=(-a+c)·=c2=|a|2,所以cos
〈,〉==,
即异面直线CE与AC′所成角的余弦值为.
答案:垂直
四、解答题(每小题10分,共20分)
9.如图,三棱锥P ABC中,点G为△ABC的重心,点M在PG上,且PM=3MG,过点M任意作一个平面分别交线段PA,PB,PC于点D,E,F,若=m,=n,=t,求证:++为定值,并求出该定值.
【解析】连接AG并延长交BC于点H(图略),由题意,可令{,,}为空间的一个基底,
==(+)=+×=+×=+(-)+(-)=++.
连接DM,因为点D,E,F,M共面,
所以存在实数λ,μ使得=λ+μ,即-=λ(-)+μ(-),所以=(1-λ-μ)+λ+μ=(1-λ-μ)m+λn+μt,由空间向量基本定理,知=(1-λ-μ)m,=λn,=μt,
所以++=4(1-λ-μ)+4λ+4μ=4,为定值.
10.如图,正四面体V ABC的高VD的中点为O,VC的中点为M.
(1)求证:AO,BO,CO两两垂直;
(2)求〈,〉.
【解析】设=a,=b,=c,正四面体的棱长为1,
(1)因为=(a+b+c),=(b+c-5a),=(a+c-5b),=(a+b-5c),
所以·=(b+c-5a)·(a+c-5b)
=(18a·b-9|a|2)
==0,
所以⊥,即AO⊥BO.
同理,AO⊥CO,BO⊥CO.
所以AO,BO,CO两两垂直.
(2)=+=-(a+b+c)+c
=(-2a-2b+c),
所以||==.
又||==,
·=(-2a-2b+c)·(b+c-5a)=,
所以cos
〈,〉==.
又〈,〉∈[0,π],所以〈,〉=.
拓展
1.如图,在梯形ABCD中,AB∥CD,AB=2CD,点O为空间任一点,设=a,=b,=c,则向量用a,b,c表示为________.
【解析】因为=-2,
所以-=-2(-),
所以b-a=-2(-c),所以=a-b+c.
答案:a-b+c
2.如图,已知平行六面体ABCD A1B1C1D1的底面ABCD是菱形,且∠C1CB=∠C1CD=∠BCD=60°.当的值等于多少时,能使A1C⊥平面C1BD
【解析】不妨设=x,CC1=1,
由A1C⊥平面C1BD,得A1C⊥C1B,A1C⊥C1D,
=+,==++,
由·=0,得(++)·(+)=·+·=0,
注意到·+·=-,
可得方程1-x2+=0,解得x=1或x=-(舍去),
因此,当=1时,能使A1C⊥平面C1BD.
PAGE
基础练 (15分钟 30分)
1.已知边长为1的正方体ABCD A1B1C1D1的上底面A1B1C1D1的中心为O1,则·的值为( )
A.-1
B.0
C.1
D.2
2.若{e1,e2,e3}是空间向量的一个基底,又a=e1+e2+e3,b=e1+e2-e3,c=e1-e2+e3,d=e1+2e2+3e3,d=xa+yb+zc,则x,y,z的值分别为( )
A.,-1,-
B.-1,,-
C.,1,
D.-,1,
3.已知a,b是异面直线,A,B∈a,C,D∈b,AC⊥b,BD⊥b,且AB=2,CD=1,则a,b所成的角是________.
4.{a,b,c}为空间的一个基底,且存在实数x,y,z使得xa+yb+zc=0,则x=________,y=________,z=________.
5.如图,四棱锥P OABC的底面为一矩形,PO⊥平面OABC,设=a,=b,=c,E,F分别是PC和PB的中点,用a,b,c表示,,,.
能力练(30分钟 60分)
一、单选题(每小题5分,共20分)
1.O,A,B,C为空间四点,且向量,,不能构成空间的一个基底,则( )
A.,,共线
B.,共线
C.,共线
D.O,A,B,C四点共面
2.在长方体ABCD A1B1C1D1中,AC与BD的交点为M,设=a,=b,=c,则下列向量中与相等的向量是
( )
A.-a+b+c
B.a+b+c
C.a-b+c
D.-a-b+c
3.已知在空间四边形ABCD中,∠ACD=∠BDC=90°,且AB=2,CD=1,则AB与CD所成的角是( )
A.30°
B.45°
C.60°
D.90°
4.点P是矩形ABCD所在平面外一点,且PA⊥平面ABCD,M,N分别是PC,PD上的点,且=,=,则满足=x+y+z的实数x,y,z的值分别为( )
A.-,,
B.,-,
C.-,,-
D.-,-,
二、多选题(每小题5分,共10分,全部选对得5分,选对但不全的得3分,有选错的得0分)
5.下列说法正确的是( )
A.若两个非零向量a,b与任何一个向量都不能构成空间的一个基底,则a,b共线
B.空间的基底有且仅有一个
C.两两垂直的三个非零向量可以构成空间的一个基底
D.基底{a,b,c}中基向量与基底{e,f,g}中基向量对应相等
6.已知在空间四面体O ABC中,点M在线段OA上,且OM=2MA,点N为BC中点,设=a,=b,=c,则( )
A.=a+b-c
B.=-a+b+c
C.=a-c
D.=a+b-c
三、填空题(每小题5分,共10分)
7.在空间中平移△ABC到△A1B1C1(使△A1B1C1与△ABC不共面),连接对应顶点.设=a,=b,=c,M是BC1的中点,N是B1C1的中点,用基底{a,b,c}表示向量+的结果为________.
8.如图,直三棱柱ABC A′B′C′中,AC=BC=AA′,∠ACB=90°,D,E分别为AB,BB′的中点.
则CE与A′D的位置关系是________;异面直线CE与AC′所成角的余弦值是________.
四、解答题(每小题10分,共20分)
9.如图,三棱锥P ABC中,点G为△ABC的重心,点M在PG上,且PM=3MG,过点M任意作一个平面分别交线段PA,PB,PC于点D,E,F,若=m,=n,=t,求证:++为定值,并求出该定值.
10.如图,正四面体V ABC的高VD的中点为O,VC的中点为M.
(1)求证:AO,BO,CO两两垂直;
(2)求〈,〉.
拓展
1.如图,在梯形ABCD中,AB∥CD,AB=2CD,点O为空间任一点,设=a,=b,=c,则向量用a,b,c表示为________.
2.如图,已知平行六面体ABCD A1B1C1D1的底面ABCD是菱形,且∠C1CB=∠C1CD=∠BCD=60°.当的值等于多少时,能使A1C⊥平面C1BD
参考答案:
基础练 (15分钟 30分)
1.已知边长为1的正方体ABCD A1B1C1D1的上底面A1B1C1D1的中心为O1,则·的值为( )
A.-1
B.0
C.1
D.2
【解析】选C.==+=+(+),而=+,
则·=(2+2)=1.
2.若{e1,e2,e3}是空间向量的一个基底,又a=e1+e2+e3,b=e1+e2-e3,c=e1-e2+e3,d=e1+2e2+3e3,d=xa+yb+zc,则x,y,z的值分别为( )
A.,-1,-
B.-1,,-
C.,1,
D.-,1,
【解析】选A.由题意得,d=xa+yb+zc=x(e1+e2+e3)+y(e1+e2-e3)+z(e1-e2+e3)=(x+y+z)e1+(x+y-z)e2+(x-y+z)e3=e1+2e2+3e3,由空间向量基本定理,得解得
3.已知a,b是异面直线,A,B∈a,C,D∈b,AC⊥b,BD⊥b,且AB=2,CD=1,则a,b所成的角是________.
【解析】=++,
所以·=·(++)=||2=1,
所以cos
〈,〉==,
所以异面直线a,b所成的角是60°.
答案:60°
4.{a,b,c}为空间的一个基底,且存在实数x,y,z使得xa+yb+zc=0,则x=________,y=________,z=________.
【解析】若x,y,z中存在一个不为0的数,不妨设x≠0,则a=-b-c,所以a,b,c共面.这与{a,b,c}是基底矛盾,故x=y=z=0.
答案:0 0 0
5.如图,四棱锥P OABC的底面为一矩形,PO⊥平面OABC,设=a,=b,=c,E,F分别是PC和PB的中点,用a,b,c表示,,,.
【解析】==-=-(+)=-a-b+c;
=-=(+)-(+)
=--+=-a-b+c;
=-=(+)-
=-a+b+c;
===a.
能力练(30分钟 60分)
一、单选题(每小题5分,共20分)
1.O,A,B,C为空间四点,且向量,,不能构成空间的一个基底,则( )
A.,,共线
B.,共线
C.,共线
D.O,A,B,C四点共面
【解析】选D.由题意知,向量,,共面,从而O,A,B,C四点共面.
2.在长方体ABCD A1B1C1D1中,AC与BD的交点为M,设=a,=b,=c,则下列向量中与相等的向量是
( )
A.-a+b+c
B.a+b+c
C.a-b+c
D.-a-b+c
【解析】选A.=+
=+=+(+)
=+=c+(-a+b)
=-a+b+c.
3.已知在空间四边形ABCD中,∠ACD=∠BDC=90°,且AB=2,CD=1,则AB与CD所成的角是( )
A.30°
B.45°
C.60°
D.90°
【解析】选C.由题意得·=·=0,
所以·=(++)·=·+
||2+·=||2=1,所以cos
〈,〉==,所以AB与CD所成的角为60°.
4.点P是矩形ABCD所在平面外一点,且PA⊥平面ABCD,M,N分别是PC,PD上的点,且=,=,则满足=x+y+z的实数x,y,z的值分别为( )
A.-,,
B.,-,
C.-,,-
D.-,-,
【解析】选D.如图所示,取PC的中点E,连接NE,
则=-=-(-)
=-=-
=--(-++)=--+,又=x+y+z,则x=-,y=-,z=.
二、多选题(每小题5分,共10分,全部选对得5分,选对但不全的得3分,有选错的得0分)
5.下列说法正确的是( )
A.若两个非零向量a,b与任何一个向量都不能构成空间的一个基底,则a,b共线
B.空间的基底有且仅有一个
C.两两垂直的三个非零向量可以构成空间的一个基底
D.基底{a,b,c}中基向量与基底{e,f,g}中基向量对应相等
【解析】选AC.A项中若a,b不共线,则任意与a,b不共面的向量就可以和a,b构成空间的一个基底,A对;B项中空间基底有无数个,B错;C项显然正确;D项中因为基底不唯一,所以D错.
6.已知在空间四面体O ABC中,点M在线段OA上,且OM=2MA,点N为BC中点,设=a,=b,=c,则( )
A.=a+b-c
B.=-a+b+c
C.=a-c
D.=a+b-c
【解析】选BC.=(+)=c+b-a;=-=(+)-=b+c-a;
=+=-c+a;=+=a-b.
三、填空题(每小题5分,共10分)
7.在空间中平移△ABC到△A1B1C1(使△A1B1C1与△ABC不共面),连接对应顶点.设=a,=b,=c,M是BC1的中点,N是B1C1的中点,用基底{a,b,c}表示向量+的结果为________.
【解析】如图,
+=(+)+
=+=b+(a+b)+(a+c)
=a+b+c.
答案:a+b+c
8.如图,直三棱柱ABC A′B′C′中,AC=BC=AA′,∠ACB=90°,D,E分别为AB,BB′的中点.
则CE与A′D的位置关系是________;异面直线CE与AC′所成角的余弦值是________.
【解析】设=a,=b,=c,
根据题意,|a|=|b|=|c|且a·b=b·c=c·a=0,所以=b+c,=-c+b-a.所以·=-c2+b2=0.所以⊥,即CE与
A′D垂直;因为=-a+c,所以||=|a|.又||=|a|,·=(-a+c)·=c2=|a|2,所以cos
〈,〉==,
即异面直线CE与AC′所成角的余弦值为.
答案:垂直
四、解答题(每小题10分,共20分)
9.如图,三棱锥P ABC中,点G为△ABC的重心,点M在PG上,且PM=3MG,过点M任意作一个平面分别交线段PA,PB,PC于点D,E,F,若=m,=n,=t,求证:++为定值,并求出该定值.
【解析】连接AG并延长交BC于点H(图略),由题意,可令{,,}为空间的一个基底,
==(+)=+×=+×=+(-)+(-)=++.
连接DM,因为点D,E,F,M共面,
所以存在实数λ,μ使得=λ+μ,即-=λ(-)+μ(-),所以=(1-λ-μ)+λ+μ=(1-λ-μ)m+λn+μt,由空间向量基本定理,知=(1-λ-μ)m,=λn,=μt,
所以++=4(1-λ-μ)+4λ+4μ=4,为定值.
10.如图,正四面体V ABC的高VD的中点为O,VC的中点为M.
(1)求证:AO,BO,CO两两垂直;
(2)求〈,〉.
【解析】设=a,=b,=c,正四面体的棱长为1,
(1)因为=(a+b+c),=(b+c-5a),=(a+c-5b),=(a+b-5c),
所以·=(b+c-5a)·(a+c-5b)
=(18a·b-9|a|2)
==0,
所以⊥,即AO⊥BO.
同理,AO⊥CO,BO⊥CO.
所以AO,BO,CO两两垂直.
(2)=+=-(a+b+c)+c
=(-2a-2b+c),
所以||==.
又||==,
·=(-2a-2b+c)·(b+c-5a)=,
所以cos
〈,〉==.
又〈,〉∈[0,π],所以〈,〉=.
拓展
1.如图,在梯形ABCD中,AB∥CD,AB=2CD,点O为空间任一点,设=a,=b,=c,则向量用a,b,c表示为________.
【解析】因为=-2,
所以-=-2(-),
所以b-a=-2(-c),所以=a-b+c.
答案:a-b+c
2.如图,已知平行六面体ABCD A1B1C1D1的底面ABCD是菱形,且∠C1CB=∠C1CD=∠BCD=60°.当的值等于多少时,能使A1C⊥平面C1BD
【解析】不妨设=x,CC1=1,
由A1C⊥平面C1BD,得A1C⊥C1B,A1C⊥C1D,
=+,==++,
由·=0,得(++)·(+)=·+·=0,
注意到·+·=-,
可得方程1-x2+=0,解得x=1或x=-(舍去),
因此,当=1时,能使A1C⊥平面C1BD.
PAGE
