1.1.3 集合的基本运算

(共31张PPT)
A
B
新课导入
集合之间的基本关系是类比实数之间的关系得到的，同样类比实数的运算，能否得到集合之间的运算呢？
想一想
实数有加法运算，那么集合是否也有“加法”呢？
下列各个集合，你能说出集合C与集合A，B之间的关系吗？
（1）A={a，b}，B={c，d },C={a，b，c，d};
（2）A={x∣x是有理数}，B={x ∣x是无理数}，
C={x ∣x是实数}；
（3）A={x|1观 察
集合A
集合B
集合C
A
2
4
6
8
10
-2
B
C
请观察A，B，C这些集合之间是什么关系？
a,b
c,d
a,b,c,d
x是有理数
x是无理数
x是实数
集合C是由所有属于集合A或属于集合B的元素组成.
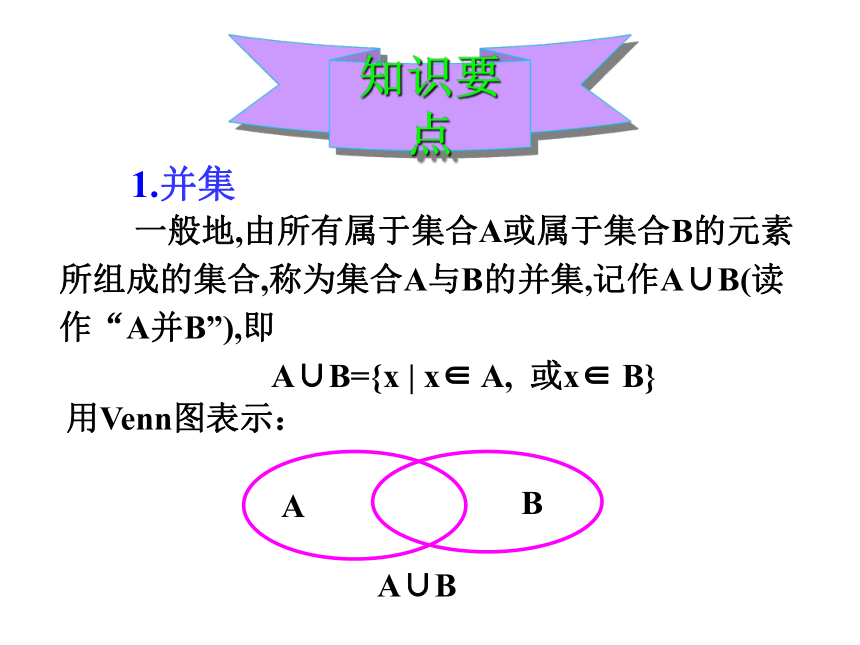
一般地,由所有属于集合A或属于集合B的元素所组成的集合,称为集合A与B的并集,记作A∪B(读作“A并B”),即
A∪B={x | x∈ A, 或x∈ B}
知识要点
1.并集
用Venn图表示：
A
B
A∪B
B
A
A∪B=B
注意
例 设A={a,b,c}, B={a,c,d,f},求A∪B.
解: A∪B={a,b,c} ∪ {a,c,d,f}
={a,b,c,d,f}
例 设集合A={x|-4解: A∪B={x|-4={x|-4注意：求两个集合的并集时，它们的公共元素在并集中只能出现一次.如：a,c.
在数轴上表示并集
-4
-3
-2
-1
0
1
2
3
4
A
B
A∪B
观 察
下列各个集合,你能说出集合A,B与集合C之间的关系吗
(1)A={2,4,6,8,10},B={2,3,5,8,9,12},C={2,8};
(2) A={x|1集合C是由那些既属于集合A且又属于集合B的所有元素组成.
2.交集
一般地,由属于集合A且属于集合B的所有元素组成的集合,称为A与B的交集,记作A∩B,(读作“A交B”),即
A∩B={x|x∈A,且x∈B}
知识要点
用Venn图表示：
A
B
A∩B
B
A
注意
A∩B=A
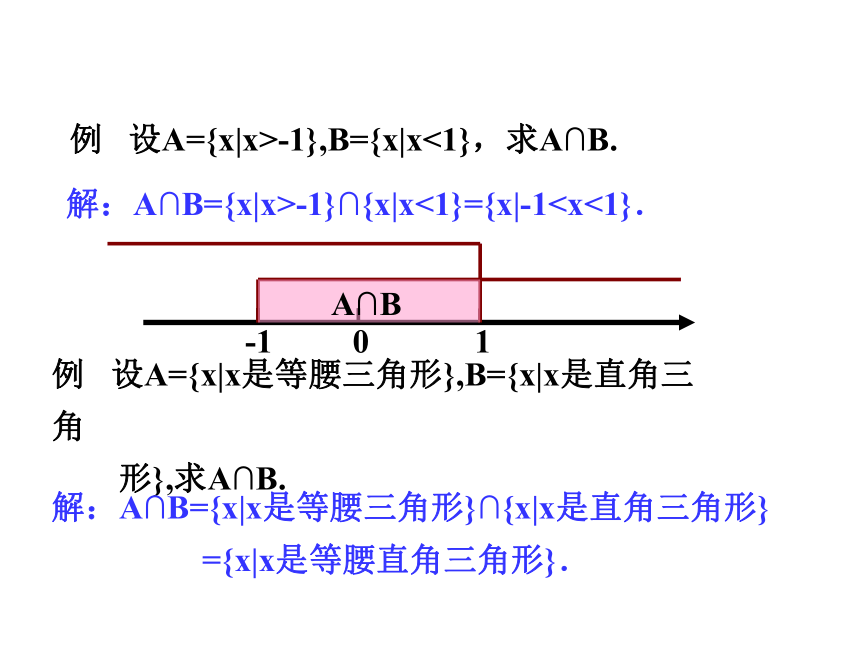
例 设A={x|x>-1},B={x|x<1}，求A∩B.
例 设A={x|x是等腰三角形},B={x|x是直角三角
形},求A∩B.
解：A∩B={x|x>-1}∩{x|x<1}={x|-1解：A∩B={x|x是等腰三角形}∩{x|x是直角三角形}
={x|x是等腰直角三角形}．
1
-1
0
A∩B
方程 的解集，在有理数范围内有几个解？分别是什么？
在不同的范围内研究问题，结果是不同的，为此，需要确定研究对象的范围.
想一想
在实数范围内有几个解？分别是什么？
1个 ，{1}
一般地,如果一个集合含有我们所研究问题中所涉及的所有元素,那么就称这个集合为全集,通常记作U.
通常也把给定的集合作为全集.
知识要点
对于一个集合A,由全集U中不属于A的所有元素组成的集合称为集合A相对于全集U的补集,简称为集合A的补集.
补集可用Venn图表示为:
如果全集U是明确的，那么全集U可以省略不写，将
简记为
读作“A的补集”．
U
UA
A
对于任意的一个集合A都有
（2）
（3）
（1）
U
UA
A
例 设
求
解： 将集合
用数轴表示为
所以
-1
0
1
2
3
x
求用区间表示的集合的补集时，要特别注意区间端点的归属．
例 设U={x|x是小于7的正整数},A={1，2，3}，B={3，4，5，6},求 UA, UB.
例 设全集U=R, M={x|x≥1}，N={x|0≤x＜1}，
则 U M， U N.
解：根据题意可知 U M={x|x<1}，
U N={x|x<0且x≥1}.
解:根据题意可知,U={1,2,3,4,5,6},
所以 UA={4,5,6} UB={1,2} .
例 设A＝{x|－3≤x≤3}，B＝{x|－4≤x≤1}，C
＝
(3)(A∪B)∩C；(4) (A∩C)∪B.
，求(1)A∩B；(2) B∪C；
解：(1)A∩B＝{x|－3≤x≤1}
(2) B∪C＝
(3) (A∪B)∩C＝
(4) (A∩C)∪B＝{x|－4≤x≤3}
注意：用数轴来处理比较简捷（数形结合思想）
例 设集合A＝{－4，2m－1，m2}，
B＝{9，m－5，1－m}，又A∩B＝{9}，求A∪B
解：(1) 若2m-1＝9，得m＝5，得
A＝{-4,9,25}，B＝{9,0,-4}，
得A∩B＝{-4,9}，不符合题.
(2) 若m2＝9，得m＝3或m＝-3，m＝3时，
A＝{-4,5,9}，B＝{9,-2,-2}
违反互异性，舍去. 当m＝-3时，
A＝{-4,-7,9}，B＝{9,-8,4}
符合题意。此时A∪B＝{-4,-7,9,-8,4}
由(1)(2)可知：m＝-3，
A∪B＝{-4,-7,9,-8,4}
例 已知U＝R，A＝{x|x－3＞0}，
B＝{x|(x＋2)(x－4)≤0}，
求： (1) ∪(A∪B) (2) ∪(A∩B)
解：（1） ∪(A∪B)=
（2） ∪(A∩B)={x|x≤3或x＞4}
(1)运算顺序：括号、补、交并；
(2)注意端点值是否可以取到；
(3)运算性质： ∪(A∪B)＝ ∪A∩ ∪B,
∪(A∩B)＝ ∪A∪ ∪B， ∪A∩A＝Φ，
∪A∪A＝U， ∪( ∪A)＝A.
注意
B＝{x|0≤x≤3}，C＝
例 已知U＝
求：(1) ∪C； (2) ∪A∪B； (3) ∪A∪( ∪B∩C)
(1)注意全集不是R；
(2)用数轴来处理；
(3)注意端点值是否可以取到.
注意
解：（1） ∪C=
(2) ∪A∪B=
(3) ∪A∪( ∪B∩C)=
课堂小结
集合运算
补运算
并运算
交运算
进行以不等式描述的或以区间形式出现的集合间的并、交、补运算时，一定要画数轴帮助分析.
（1）运算顺序：括号、补、交并；
（2）运算性质：
∪(A∪B)＝ ∪A∩ ∪B；
∪(A∩B)＝ ∪A∪ ∪B；
∪A∩A＝Φ， ∪A∪A＝U， ∪( ∪A)＝A.
课堂练习
√
×
×
1.判断正误.
（1）若U={四边形}，A={梯形}，则 UA={平行四边形}
（2）若U是全集，且A B，则 UA CUB
（3）若U={1，2}，A=U，则 UA=
2.
求
3．
求
-2
-1
0
1
2
3
4
A
B
解:将集合A、B在数轴上表示（如图），
4.设
求
所以
5.设
求
解：解方程组
得
所以
x
-1
0
1
2
3
A
B
6. 设A={2,-1,x2-2x+1}, B={2y,-4,x+1}, C={-1,4} 且A∩B=C,求x,y
解：由A∩B=C知 4 A
∴必然 x2－2x+1=4 得
x1=-1, x2=3
由x=－1 得 x+1=0 C
∴x －1 ∴x=3 x+1=4 C
此时2y=－1 ,∴y=－1/2
∴综上所述x=3 , y=－1/2.