2021年新教材高中数学2.4.2圆的一般方程(Word含解析)
文档属性
| 名称 | 2021年新教材高中数学2.4.2圆的一般方程(Word含解析) | 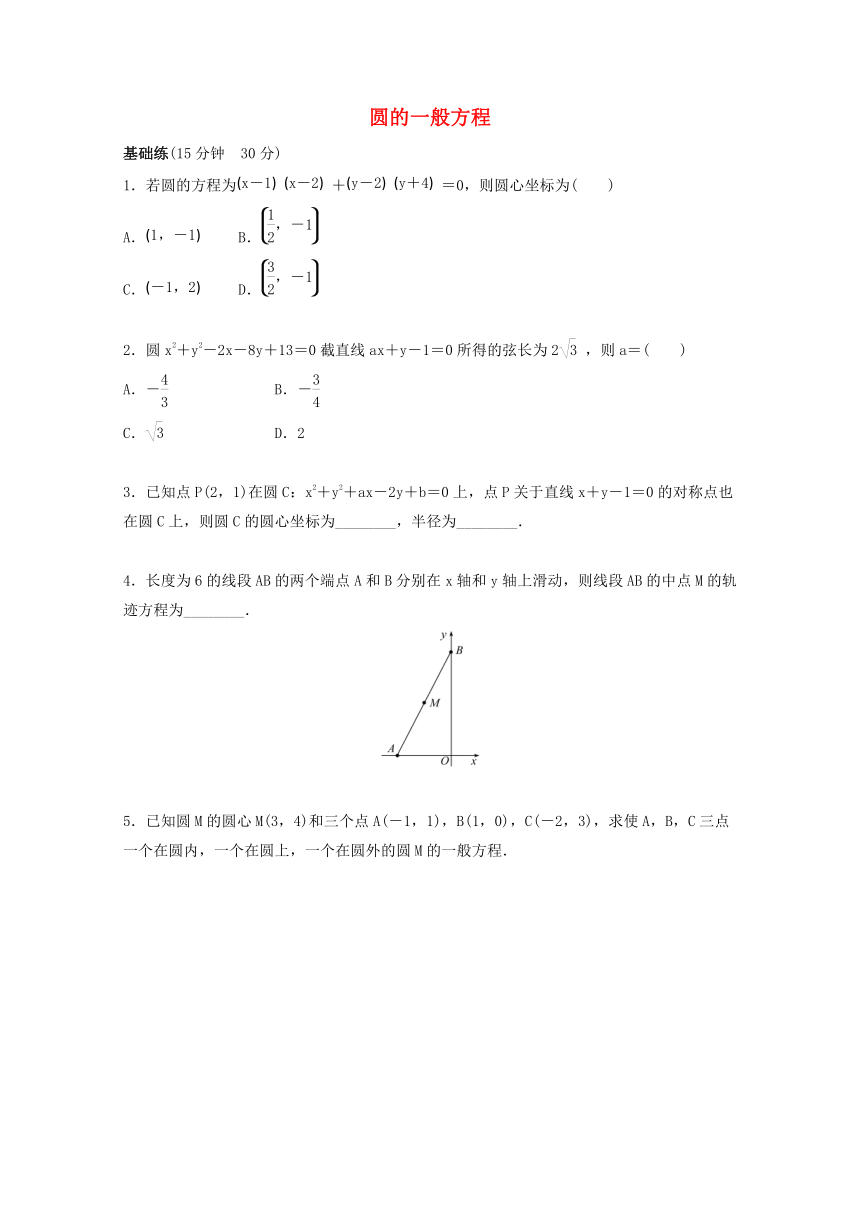 | |
| 格式 | doc | ||
| 文件大小 | 165.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-09 14:30:56 | ||
图片预览




文档简介
圆的一般方程
基础练(15分钟 30分)
1.若圆的方程为+=0,则圆心坐标为( )
A.
B.
C.
D.
2.圆x2+y2-2x-8y+13=0截直线ax+y-1=0所得的弦长为2,则a=( )
A.-
B.-
C.
D.2
3.已知点P(2,1)在圆C:x2+y2+ax-2y+b=0上,点P关于直线x+y-1=0的对称点也在圆C上,则圆C的圆心坐标为________,半径为________.
4.长度为6的线段AB的两个端点A和B分别在x轴和y轴上滑动,则线段AB的中点M的轨迹方程为________.
5.已知圆M的圆心M(3,4)和三个点A(-1,1),B(1,0),C(-2,3),求使A,B,C三点一个在圆内,一个在圆上,一个在圆外的圆M的一般方程.
能力练(30分钟 60分)
一、单选题(每小题5分,共20分)
1.若x,y满足x2+y2-2x+4y-20=0,则x2+y2的最小值是( )
A.-5
B.5-
C.30-10
D.无法确定
2.方程|x|-1=表示的曲线是( )
A.—个圆
B.两个圆
C.一个半圆
D.两个半圆
3.过点P且被圆C:x2+y2-2x-4y=0截得弦最长的直线l的方程是( )
A.3x-y+5=0
B.x-3y+5=0
C.3x+y-5=0
D.x-3y-5=0
4.圆x2+y2-2x-2y+1=0上的点到直线x-y=2的距离最大值是( )
A.2
B.1+
C.1+
D.2+2
二、多选题(每小题5分,共10分,全部选对得5分,选对但不全的得3分,有选错的得0分)
5.已知圆C经过点(1,0),且圆心C是两直线x=1与x+y=2的交点,则下列点在圆内的有( )
A.(0,0)
B.
C.(3,1)
D.(1,1)
6.如果圆(x-a)2+(y-a)2=8上总存在到原点的距离为的点,则实数a的值可以是( )
A.-2
B.0
C.1
D.3
三、填空题(每小题5分,共10分)
7.已知圆C:x2+y2-2x+2y-3=0,AB为圆C的一条直径,点A的坐标为,则点B的坐标为________.
8.已知圆x2+y2+kx+2y=-k2,当该圆的面积取最大值时,圆心坐标为________.
四、解答题(每小题10分,共20分)
9.自圆C:(x-3)2+(y+4)2=4外一点P(x,y)引该圆的一条切线,切点为Q,PQ的长度等于点P到原点O的距离,求点P的轨迹方程.
10.已知圆C的方程为x2+(y-4)2=1,直线l的方程为2x-y=0,点P在直线l上,过点P作圆C的切线PA,PB,切点为A,B.
(1)若∠APB=60°,求点P的坐标;
(2)求证:经过A,P,C(其中点C为圆C的圆心)三点的圆必经过定点,并求出所有定点的坐标.
拓展
已知点P(2,2),圆C:x2+y2-8y=0,过点P的动直线l与圆C交于A,B两点,线段AB的中点为M,O为坐标原点.
(1)求M的轨迹方程;
(2)当=时,求l的方程及△POM的面积.
参考答案:
基础练(15分钟 30分)
1.若圆的方程为+=0,则圆心坐标为( )
A.
B.
C.
D.
【解析】选D.圆的方程可化为+(y+1)2=,所以圆心坐标为.
2.圆x2+y2-2x-8y+13=0截直线ax+y-1=0所得的弦长为2,则a=( )
A.-
B.-
C.
D.2
【解析】选A.圆的方程可化为2+2=4,
所以圆心坐标为,由点到直线的距离公式得:d==1,解得a=-.
3.已知点P(2,1)在圆C:x2+y2+ax-2y+b=0上,点P关于直线x+y-1=0的对称点也在圆C上,则圆C的圆心坐标为________,半径为________.
【解析】点P关于直线x+y-1=0的对称点为P′,将P和P′的坐标代入圆C的方程的方程组解得
所以圆的方程为x2+y2-2y-3=0,
即x2+2=4,
所以圆心的坐标为,半径为2.
答案: 2
4.长度为6的线段AB的两个端点A和B分别在x轴和y轴上滑动,则线段AB的中点M的轨迹方程为________.
【解析】设M(x,y),因为△AOB是直角三角形,所以|OM|=|AB|=3为定值,故M的轨迹为以O为圆心,3为半径的圆,故x2+y2=9即为所求.
答案:x2+y2=9
5.已知圆M的圆心M(3,4)和三个点A(-1,1),B(1,0),C(-2,3),求使A,B,C三点一个在圆内,一个在圆上,一个在圆外的圆M的一般方程.
【解析】因为==5,
==2,
==,
所以<<.
所以点B在圆内,点A在圆上,点C在圆外.
所以圆的半径r==5,
所以圆M的方程为(x-3)2+(y-4)2=25,
即x2+y2-6x-8y=0.
能力练(30分钟 60分)
一、单选题(每小题5分,共20分)
1.若x,y满足x2+y2-2x+4y-20=0,则x2+y2的最小值是( )
A.-5
B.5-
C.30-10
D.无法确定
【解析】选C.把圆的方程化为标准方程得:(x-1)2+(y+2)2=25,
则圆心A坐标为(1,-2),圆的半径r=5,设圆上一点的坐标为(x,y),原点O坐标为(0,0),
则=,r=5,
所以圆上一点到原点O最小距离为5-.
则x2+y2的最小值为(5-)2=30-10.
2.方程|x|-1=表示的曲线是( )
A.—个圆
B.两个圆
C.一个半圆
D.两个半圆
【解析】选D.方程可化为2+2=1.
又|x|-1≥0,所以x≤-1或x≥1.
若x≤-1时,则方程为2+2=1;
若x≥1时,则方程为2+2=1.
3.过点P且被圆C:x2+y2-2x-4y=0截得弦最长的直线l的方程是( )
A.3x-y+5=0
B.x-3y+5=0
C.3x+y-5=0
D.x-3y-5=0
【解析】选B.根据几何意义知:过P且被圆截得弦长最长的弦的直线是过圆心的直线;圆x2+y2-2x-4y=0的圆心为(1,2),
则所求直线l的斜率为k==;
则直线l方程为y-1=(x+2),即x-3y+5=0.
4.圆x2+y2-2x-2y+1=0上的点到直线x-y=2的距离最大值是( )
A.2
B.1+
C.1+
D.2+2
【解析】选B.本题考查点到直线的距离.
由x2+y2-2x-2y+1=0,
得(x-1)2+(y-1)2=1,
表示以M(1,1)为圆心,以r=1为半径的圆.
先计算点M到直线x-y=2的距离d==,圆上的点到直线的距离的最大值为点M到直线的距离x-y=2再加半径,即dmax=d+r=1+.
【误区警示】涉及与圆有关的最值问题一般转到圆心上去.圆上的点直线距离的最大值为圆心到直线的距离再加上半径.
二、多选题(每小题5分,共10分,全部选对得5分,选对但不全的得3分,有选错的得0分)
5.已知圆C经过点(1,0),且圆心C是两直线x=1与x+y=2的交点,则下列点在圆内的有( )
A.(0,0)
B.
C.(3,1)
D.(1,1)
【解析】选BD.由得
即所求圆的圆心坐标为(1,1),又由该圆过点(1,0),得其半径为1,圆的方程为(x-1)2+(y-1)2=1.将选项中4个点代入,可得只有BD满足小于1,即BD选项中的点在圆内.
6.如果圆(x-a)2+(y-a)2=8上总存在到原点的距离为的点,则实数a的值可以是( )
A.-2
B.0
C.1
D.3
【解析】选ACD.圆(x-a)2+(y-a)2=8的圆心(a,a)到原点的距离为|a|,半径r=2,由圆(x-a)2+(y-a)2=8上总存在点到原点的距离为,得2-≤|a|≤2+,
所以1≤|a|≤3,解得1≤a≤3或-3≤a≤-1.
三、填空题(每小题5分,共10分)
7.已知圆C:x2+y2-2x+2y-3=0,AB为圆C的一条直径,点A的坐标为,则点B的坐标为________.
【解题指南】圆心为直径的中点,可以先求出圆心坐标,再求点B的坐标.
【解析】由x2+y2-2x+2y-3=0得(x-1)2+(y+1)2=5,所以圆心C的坐标为,设B的坐标为(x0,y0),又A的坐标为(0,1),由中点坐标公式得解得
所以B点的坐标为.
答案:(2,-3)
8.已知圆x2+y2+kx+2y=-k2,当该圆的面积取最大值时,圆心坐标为________.
【解析】由x2+y2+kx+2y=-k2,
得+=-k2+1.
所以当-k2=0,
即k=0时圆的面积最大,此时圆心坐标为.
答案:(0,-1)
四、解答题(每小题10分,共20分)
9.自圆C:(x-3)2+(y+4)2=4外一点P(x,y)引该圆的一条切线,切点为Q,PQ的长度等于点P到原点O的距离,求点P的轨迹方程.
【解析】由题意得,圆心C的坐标为(3,-4),半径r=2,如图.
因为|PQ|=|PO|,且PQ⊥CQ,
所以|PO|2+r2=|PC|2,
所以x2+y2+4=(x-3)2+(y+4)2,即6x-8y-21=0,所以点P的轨迹方程为6x-8y-21=0.
10.已知圆C的方程为x2+(y-4)2=1,直线l的方程为2x-y=0,点P在直线l上,过点P作圆C的切线PA,PB,切点为A,B.
(1)若∠APB=60°,求点P的坐标;
(2)求证:经过A,P,C(其中点C为圆C的圆心)三点的圆必经过定点,并求出所有定点的坐标.
【解析】(1)由条件可得圆C的圆心坐标为(0,4),|PC|=2,设P(a,2a),则=2,解得a=2或a=,所以点P的坐标为(2,4)或.
(2)设P(b,2b),过点A,P,C的圆即是以PC为直径的圆,其方程为x(x-b)+(y-4)(y-2b)=0,整理得x2+y2-bx-4y-2by+8b=0,
即(x2+y2-4y)-b(x+2y-8)=0.
由解得或
所以该圆必经过定点(0,4)和.
拓展
已知点P(2,2),圆C:x2+y2-8y=0,过点P的动直线l与圆C交于A,B两点,线段AB的中点为M,O为坐标原点.
(1)求M的轨迹方程;
(2)当=时,求l的方程及△POM的面积.
【解析】(1)圆C的方程可化为x2+(y-4)2=16,
所以圆心为C(0,4),半径为4,
设M(x,y),则=(x,y-4),=(2-x,2-y),
由题设知·=0,即x(2-x)+(y-4)(2-y)=0,(x-1)2+(y-3)2=2.由于点P在圆C的内部,所以M的轨迹方程是(x-1)2+(y-3)2=2.
(2)由(1)可知M的轨迹是以点N(1,3)为圆心,为半径的圆.
由于=,故O在线段PM的垂直平分线上,又P在圆N上,从而ON⊥PM.
因为ON的斜率为3,所以l的斜率为-,
故直线l的方程为y=-x+.
又==2,O到l的距离为,=,所以,S△POM=××=,所以△POM的面积为.
PAGE
基础练(15分钟 30分)
1.若圆的方程为+=0,则圆心坐标为( )
A.
B.
C.
D.
2.圆x2+y2-2x-8y+13=0截直线ax+y-1=0所得的弦长为2,则a=( )
A.-
B.-
C.
D.2
3.已知点P(2,1)在圆C:x2+y2+ax-2y+b=0上,点P关于直线x+y-1=0的对称点也在圆C上,则圆C的圆心坐标为________,半径为________.
4.长度为6的线段AB的两个端点A和B分别在x轴和y轴上滑动,则线段AB的中点M的轨迹方程为________.
5.已知圆M的圆心M(3,4)和三个点A(-1,1),B(1,0),C(-2,3),求使A,B,C三点一个在圆内,一个在圆上,一个在圆外的圆M的一般方程.
能力练(30分钟 60分)
一、单选题(每小题5分,共20分)
1.若x,y满足x2+y2-2x+4y-20=0,则x2+y2的最小值是( )
A.-5
B.5-
C.30-10
D.无法确定
2.方程|x|-1=表示的曲线是( )
A.—个圆
B.两个圆
C.一个半圆
D.两个半圆
3.过点P且被圆C:x2+y2-2x-4y=0截得弦最长的直线l的方程是( )
A.3x-y+5=0
B.x-3y+5=0
C.3x+y-5=0
D.x-3y-5=0
4.圆x2+y2-2x-2y+1=0上的点到直线x-y=2的距离最大值是( )
A.2
B.1+
C.1+
D.2+2
二、多选题(每小题5分,共10分,全部选对得5分,选对但不全的得3分,有选错的得0分)
5.已知圆C经过点(1,0),且圆心C是两直线x=1与x+y=2的交点,则下列点在圆内的有( )
A.(0,0)
B.
C.(3,1)
D.(1,1)
6.如果圆(x-a)2+(y-a)2=8上总存在到原点的距离为的点,则实数a的值可以是( )
A.-2
B.0
C.1
D.3
三、填空题(每小题5分,共10分)
7.已知圆C:x2+y2-2x+2y-3=0,AB为圆C的一条直径,点A的坐标为,则点B的坐标为________.
8.已知圆x2+y2+kx+2y=-k2,当该圆的面积取最大值时,圆心坐标为________.
四、解答题(每小题10分,共20分)
9.自圆C:(x-3)2+(y+4)2=4外一点P(x,y)引该圆的一条切线,切点为Q,PQ的长度等于点P到原点O的距离,求点P的轨迹方程.
10.已知圆C的方程为x2+(y-4)2=1,直线l的方程为2x-y=0,点P在直线l上,过点P作圆C的切线PA,PB,切点为A,B.
(1)若∠APB=60°,求点P的坐标;
(2)求证:经过A,P,C(其中点C为圆C的圆心)三点的圆必经过定点,并求出所有定点的坐标.
拓展
已知点P(2,2),圆C:x2+y2-8y=0,过点P的动直线l与圆C交于A,B两点,线段AB的中点为M,O为坐标原点.
(1)求M的轨迹方程;
(2)当=时,求l的方程及△POM的面积.
参考答案:
基础练(15分钟 30分)
1.若圆的方程为+=0,则圆心坐标为( )
A.
B.
C.
D.
【解析】选D.圆的方程可化为+(y+1)2=,所以圆心坐标为.
2.圆x2+y2-2x-8y+13=0截直线ax+y-1=0所得的弦长为2,则a=( )
A.-
B.-
C.
D.2
【解析】选A.圆的方程可化为2+2=4,
所以圆心坐标为,由点到直线的距离公式得:d==1,解得a=-.
3.已知点P(2,1)在圆C:x2+y2+ax-2y+b=0上,点P关于直线x+y-1=0的对称点也在圆C上,则圆C的圆心坐标为________,半径为________.
【解析】点P关于直线x+y-1=0的对称点为P′,将P和P′的坐标代入圆C的方程的方程组解得
所以圆的方程为x2+y2-2y-3=0,
即x2+2=4,
所以圆心的坐标为,半径为2.
答案: 2
4.长度为6的线段AB的两个端点A和B分别在x轴和y轴上滑动,则线段AB的中点M的轨迹方程为________.
【解析】设M(x,y),因为△AOB是直角三角形,所以|OM|=|AB|=3为定值,故M的轨迹为以O为圆心,3为半径的圆,故x2+y2=9即为所求.
答案:x2+y2=9
5.已知圆M的圆心M(3,4)和三个点A(-1,1),B(1,0),C(-2,3),求使A,B,C三点一个在圆内,一个在圆上,一个在圆外的圆M的一般方程.
【解析】因为==5,
==2,
==,
所以<<.
所以点B在圆内,点A在圆上,点C在圆外.
所以圆的半径r==5,
所以圆M的方程为(x-3)2+(y-4)2=25,
即x2+y2-6x-8y=0.
能力练(30分钟 60分)
一、单选题(每小题5分,共20分)
1.若x,y满足x2+y2-2x+4y-20=0,则x2+y2的最小值是( )
A.-5
B.5-
C.30-10
D.无法确定
【解析】选C.把圆的方程化为标准方程得:(x-1)2+(y+2)2=25,
则圆心A坐标为(1,-2),圆的半径r=5,设圆上一点的坐标为(x,y),原点O坐标为(0,0),
则=,r=5,
所以圆上一点到原点O最小距离为5-.
则x2+y2的最小值为(5-)2=30-10.
2.方程|x|-1=表示的曲线是( )
A.—个圆
B.两个圆
C.一个半圆
D.两个半圆
【解析】选D.方程可化为2+2=1.
又|x|-1≥0,所以x≤-1或x≥1.
若x≤-1时,则方程为2+2=1;
若x≥1时,则方程为2+2=1.
3.过点P且被圆C:x2+y2-2x-4y=0截得弦最长的直线l的方程是( )
A.3x-y+5=0
B.x-3y+5=0
C.3x+y-5=0
D.x-3y-5=0
【解析】选B.根据几何意义知:过P且被圆截得弦长最长的弦的直线是过圆心的直线;圆x2+y2-2x-4y=0的圆心为(1,2),
则所求直线l的斜率为k==;
则直线l方程为y-1=(x+2),即x-3y+5=0.
4.圆x2+y2-2x-2y+1=0上的点到直线x-y=2的距离最大值是( )
A.2
B.1+
C.1+
D.2+2
【解析】选B.本题考查点到直线的距离.
由x2+y2-2x-2y+1=0,
得(x-1)2+(y-1)2=1,
表示以M(1,1)为圆心,以r=1为半径的圆.
先计算点M到直线x-y=2的距离d==,圆上的点到直线的距离的最大值为点M到直线的距离x-y=2再加半径,即dmax=d+r=1+.
【误区警示】涉及与圆有关的最值问题一般转到圆心上去.圆上的点直线距离的最大值为圆心到直线的距离再加上半径.
二、多选题(每小题5分,共10分,全部选对得5分,选对但不全的得3分,有选错的得0分)
5.已知圆C经过点(1,0),且圆心C是两直线x=1与x+y=2的交点,则下列点在圆内的有( )
A.(0,0)
B.
C.(3,1)
D.(1,1)
【解析】选BD.由得
即所求圆的圆心坐标为(1,1),又由该圆过点(1,0),得其半径为1,圆的方程为(x-1)2+(y-1)2=1.将选项中4个点代入,可得只有BD满足小于1,即BD选项中的点在圆内.
6.如果圆(x-a)2+(y-a)2=8上总存在到原点的距离为的点,则实数a的值可以是( )
A.-2
B.0
C.1
D.3
【解析】选ACD.圆(x-a)2+(y-a)2=8的圆心(a,a)到原点的距离为|a|,半径r=2,由圆(x-a)2+(y-a)2=8上总存在点到原点的距离为,得2-≤|a|≤2+,
所以1≤|a|≤3,解得1≤a≤3或-3≤a≤-1.
三、填空题(每小题5分,共10分)
7.已知圆C:x2+y2-2x+2y-3=0,AB为圆C的一条直径,点A的坐标为,则点B的坐标为________.
【解题指南】圆心为直径的中点,可以先求出圆心坐标,再求点B的坐标.
【解析】由x2+y2-2x+2y-3=0得(x-1)2+(y+1)2=5,所以圆心C的坐标为,设B的坐标为(x0,y0),又A的坐标为(0,1),由中点坐标公式得解得
所以B点的坐标为.
答案:(2,-3)
8.已知圆x2+y2+kx+2y=-k2,当该圆的面积取最大值时,圆心坐标为________.
【解析】由x2+y2+kx+2y=-k2,
得+=-k2+1.
所以当-k2=0,
即k=0时圆的面积最大,此时圆心坐标为.
答案:(0,-1)
四、解答题(每小题10分,共20分)
9.自圆C:(x-3)2+(y+4)2=4外一点P(x,y)引该圆的一条切线,切点为Q,PQ的长度等于点P到原点O的距离,求点P的轨迹方程.
【解析】由题意得,圆心C的坐标为(3,-4),半径r=2,如图.
因为|PQ|=|PO|,且PQ⊥CQ,
所以|PO|2+r2=|PC|2,
所以x2+y2+4=(x-3)2+(y+4)2,即6x-8y-21=0,所以点P的轨迹方程为6x-8y-21=0.
10.已知圆C的方程为x2+(y-4)2=1,直线l的方程为2x-y=0,点P在直线l上,过点P作圆C的切线PA,PB,切点为A,B.
(1)若∠APB=60°,求点P的坐标;
(2)求证:经过A,P,C(其中点C为圆C的圆心)三点的圆必经过定点,并求出所有定点的坐标.
【解析】(1)由条件可得圆C的圆心坐标为(0,4),|PC|=2,设P(a,2a),则=2,解得a=2或a=,所以点P的坐标为(2,4)或.
(2)设P(b,2b),过点A,P,C的圆即是以PC为直径的圆,其方程为x(x-b)+(y-4)(y-2b)=0,整理得x2+y2-bx-4y-2by+8b=0,
即(x2+y2-4y)-b(x+2y-8)=0.
由解得或
所以该圆必经过定点(0,4)和.
拓展
已知点P(2,2),圆C:x2+y2-8y=0,过点P的动直线l与圆C交于A,B两点,线段AB的中点为M,O为坐标原点.
(1)求M的轨迹方程;
(2)当=时,求l的方程及△POM的面积.
【解析】(1)圆C的方程可化为x2+(y-4)2=16,
所以圆心为C(0,4),半径为4,
设M(x,y),则=(x,y-4),=(2-x,2-y),
由题设知·=0,即x(2-x)+(y-4)(2-y)=0,(x-1)2+(y-3)2=2.由于点P在圆C的内部,所以M的轨迹方程是(x-1)2+(y-3)2=2.
(2)由(1)可知M的轨迹是以点N(1,3)为圆心,为半径的圆.
由于=,故O在线段PM的垂直平分线上,又P在圆N上,从而ON⊥PM.
因为ON的斜率为3,所以l的斜率为-,
故直线l的方程为y=-x+.
又==2,O到l的距离为,=,所以,S△POM=××=,所以△POM的面积为.
PAGE
