3.1用字母表示数-同步练习-2021-2022学年七年级数学上册 冀教版 (word版含答案)
文档属性
| 名称 | 3.1用字母表示数-同步练习-2021-2022学年七年级数学上册 冀教版 (word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 203.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-04 09:19:37 | ||
图片预览



文档简介
2021-2022学年七年级数学上册(冀教版)
3.1用字母表示数-同步练习
时间:60分钟
一、单选题
1.苹果原价是每千克a元,现在按八折出售,假如现在要买,那么需要付费(
)
A.元
B.元
C.元
D.元
2.如图,则第n个图形中三角形的个数是(
)
……
第1个
第2个
第3个
A.
B.
C.
D.4n
3.书店里有x本书,第一天卖出了全部的,第二天卖出了余下的,还剩(
)本书.(
)
A.
B.
C.
D.
4.十位数字是a,个位数字比十位数字的2倍少6,百位数字比十位数字大3,这个三位数是(
).
A.
B.
C.
D.
5.将一个正方形剪成个小正方形,第一次操作按照图1所示,分割出4个正方形.第二次操作按如图2所示,分割出6个正方形,第三次操作按如图3所示,按照上述规律,则第次操作,正方形的个数为(
)
A.
B.
C.
D.
6.一根长的绳子,第一次剪去绳子的,第二次剪去剩下绳子的,如此剪下去,第100次剪完后剩下绳子的长度是(
)
A.
B.
C.
D.
7.下列说法正确的是(
)
A.-a一定是负数
B.a的倒数是
C.一定是分数
D.a2一定是非负数
8.某人骑自行车t(小时)走了,若步行,则比骑自行车多用3(小时),那么骑自行车每小时比步行多走(
).
A.
B.
C.
D.
二、填空题
9.一个没有关紧的水龙头一天滴水约0.09
m3,n个这样的水龙头一天滴水约____m3.
10.某音像社对外出租光盘的收费方法是:每张光盘在租出后的头两天每天收0.80元,以后每天收0.50元.那么一张光盘在租出n天(n是大于2的自然数)应收租金___元.
11.七年级2班要添置新桌椅,使每人有一套桌椅,共有n列,其中有一列7人,其余各列每列6人,需______套桌椅,当时,共需_______套桌椅.
12.每于克x元的糖果a千克和每千克y元的糖果b千克混合后,要求总价额不变,那么混合糖果的售价定为每千克_______元.
13.实验中学初三年级12个班中共有团员a人,则表示的实际意义是_________.
14.图中阴影部分的面积为__________.
15.如图是用棋子摆成的“上”字:如果按照以下规律继续摆下去,第n个“上”字需用______枚棋子.
16.礼堂第一排有
个座位,后面每排都比第一排多
个座位,则第
排座位有________________.
三、解答题
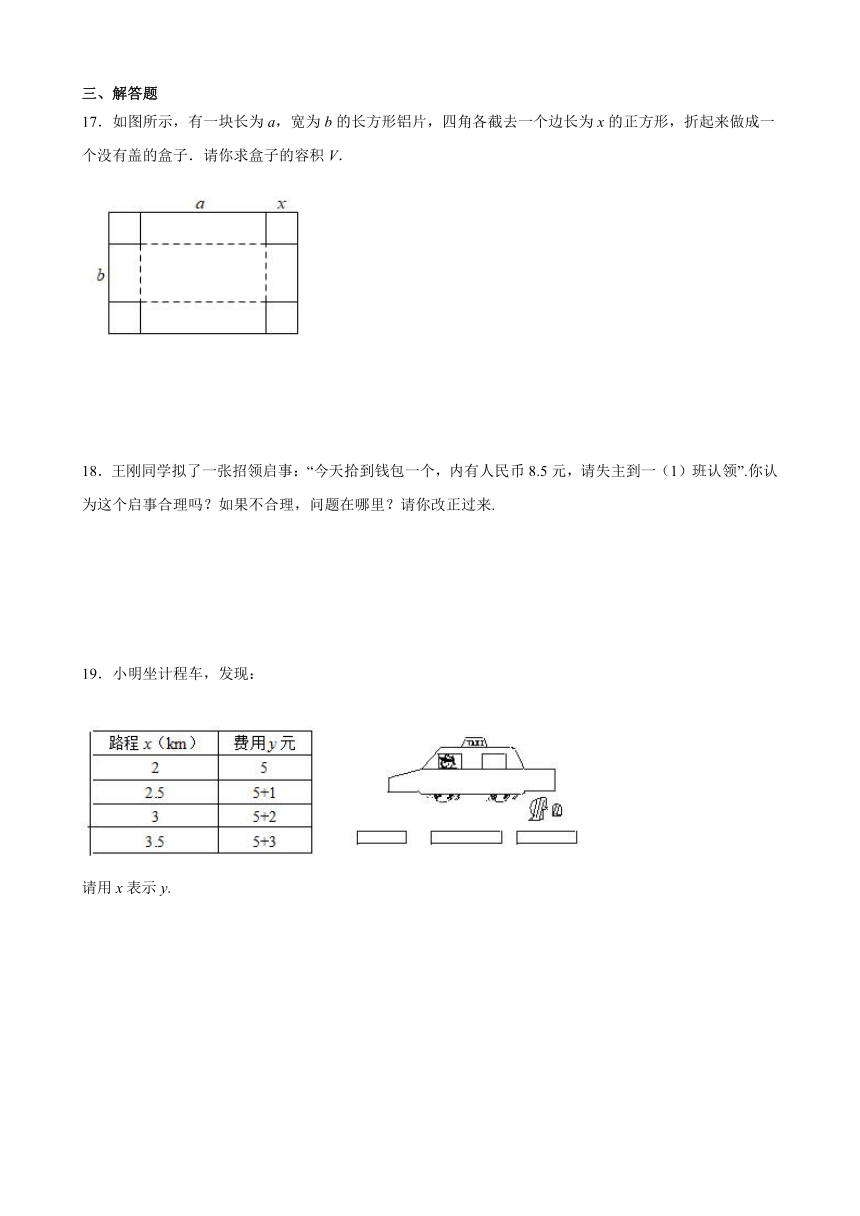
17.如图所示,有一块长为a,宽为b的长方形铝片,四角各截去一个边长为x的正方形,折起来做成一个没有盖的盒子.请你求盒子的容积V.
18.王刚同学拟了一张招领启事:“今天拾到钱包一个,内有人民币8.5元,请失主到一(1)班认领”.你认为这个启事合理吗?如果不合理,问题在哪里?请你改正过来.
19.小明坐计程车,发现:
请用x表示y.
20.一种长方形餐桌的四周可坐6人用餐,现把若干张这样的餐桌按如图方式进行拼接.
(1)若把4张、8张这样的餐桌拼接起来,四周分别可坐多少人?
(2)若用餐的人数有90人,则这样的餐桌需要多少张?
21.某音像公司对外出租学习光盘的收费方法是:每张光盘出租后的前2天共收费0.8元,以后每天收费0.3元.
(1)一张光盘在出租4天后共收费多少元?
(2)一张光盘在出租n(n>2且为整数)天后共收费多少元?
22.工程队计划每天修路a米,20天可以修完,实际只用了15天,实际每天修路多少米?
(1)用式子表示实际每天修路是多少米?
(2)根据多个式子,求时,实际每天修路多少米?
23.将一个长方形纸片连续对折,对折的次数越多,折痕的条数也就越多,如第一次对折后,有1条折痕,第2次对折后,共有3条折痕.
(1)第3次对折后共有多少条折痕?第4次对折后呢?
(2)对折多少次后折痕会超过100条?
(3)请找出折痕条数与对折次数的对应规律,写出对折n次后,折痕有多少条?
试卷第1页,共3页
参考答案
1.A
【解析】解:苹果原价是每千克a元,现在按八折出售,那么现价为,
∴根据“质量×单价=支付费用”可知需要付费为(元).
故选A.
2.D
【解析】由图可知:第1个图形的三角形个数为4个;
第2个图形的三角形个数为8个;
第3个图形的三角形个数为12个
…
∴第n个图形的三角形个数为4n个;
故选D.
3.D
【解析】解:∵书店有书x本,第一天卖出了全部的,
∴第一天还余下(x x)本,
∵第二天卖出了余下的,
∴还剩下x
x
(x x)本;
故选D.
4.A
【解析】解:∵十位数字是a,个位数字比十位数字的2倍少6,百位数字比十位数字大3,
∴个位数字为,百位数字为
,
∴这个三位数为
,
故选A.
5.D
【解析】解:图1分割出1+1+2×1=4个正方形,
图2分割出1+1+2×2=6个正方形,
图3分割出1+1+2×3=8个正方形,
…
则第n次操作,正方形的个数为1+1+2n=2n+2,
故选:D.
6.C
【解析】∵第一次剪去绳子的
,还剩
原长
第二次剪去剩下绳子的
,还剩
上次剩下的长度
因此每次减绳子后的长度都是上次剩下长度的
根据乘方的定义,我们得出第n次剪去绳子的
,还剩
第100次剪去绳子的
,还剩
故答案为:C.
7.D
【解析】A、当a是负数时,-a是正数,故本选项错误;
B、当a是0时,a没有倒数,故本选项错误;
C、当a=4时,
=2,是整数,故本选项错误;
D、
一定是非负数,本选项正确,
故选D.
8.B
【解析】骑自行车的速度为:
步行速度为:
骑自行车比步行每小时快出的路程:.
故选B
9.0.09n
【解析】一个没有关紧的水龙头一天滴水约0.09
m3,n个这样的水龙头一天滴水约0.09n
m3,
故答案为:0.09n.
10.0.5n+0.6
【解析】由题意可得,应收租金为:
=1.6+0.5n-1
=0.5n+0.6
故答案为0.5n+0.6
11.
37
【解析】总人数为7 +(n - 1)× 6 = 人,
桌椅数为套,
当时,6n+ 1 = 6×6+1 = 37套,
故答案为:;37.
12.
【解析】∵每于克x元的糖果a千克和每千克y元的糖果b千克,
∴总价格,
∴混合糖果的售价定为.
故答案是.
13.平均每班团员数
【解析】解:表示的实际意义是平均每班团员数.
故答案为平均每班团员数.
14.
【解析】设三个三角形的底分别为,,,则,
由图可知:
;
故答案是:.
15.(4n+2).
【解析】解:∵第一个“上”字需用6枚棋子,第二个“上”字需用10枚棋子,第三个“上”字需用14枚棋子,
∴依次多4个
∴第n个“上”字需用(4n+2)枚棋子.
故答案为:(4n+2).
16.
【解析】解:∵第一排有
个座位,
∴第2排的座位为a+1,
第3排的座位数为a+2,
…
第n排座位有
(a+n-1)个.
故答案为:(a+n-1).
17.
【解析】解:将这块铝片折成盒子后,盒子的形状为长方体,其底面是一个长为,宽为的长方形,盒子的高为x,
所以,盒子的容积.
18.不合理
【解析】解:不合理,问题出在8.5元上,应该写为n元.
19.y=5+.
【解析】由题意得,y=5+.
20.(1)4张长方形餐桌的四周可坐18人,8张长方形餐桌的四周可坐34人;(2)这样的餐桌需要22张.
【解析】解:(1)根据图中的规律可得:
当n=4时,4n+2=4×4+2=18(人);
当n=8时,4n+2=4×8+2=34(人),
答:当4张餐桌拼在一起时,可以坐18人;当8张餐桌拼在一起时,可以坐标34人;
(2)因为用餐的人数是90人,
根据题意可得:4n+2=90,
解得:n=22,
答:需要22张餐桌.
21.(1)1.4元;(2)(0.3n+0.2)元
【解析】解:(1)0.8+0.3×(4-2)=0.8+0.6=1.4(元)
答:一张光盘在出租4天后共收费1.4元;
(2)0.8+0.3(n-2)=(0.3n+0.2)元
答:一张光盘在出租n(n>2且为整数)天后共收费(0.3n+0.2)元.
22.(1)20a÷15(2)320米
【解析】(1)∵路的总长度为20a米,
∴实际每天修路的长度为20a÷15米.
答:实际每天修路的长度为20a÷15米.
(2)把a=240代入20a÷15得,
20a÷15=20×240÷15=320(米).
答:实际每天修路320米.
23.(1)第3次对折后共有7条折痕,第4次对折后有15条折痕;(2)对折7次后折痕会超过100条;(3)对折n次后,折痕有条.
【解析】(1)动手操作可知,第3次对折后的折痕条数为7条,
第4次对折后的折痕条数为15条;
(2)观察可知,第1次对折后的折痕条数为条,
第2次对折后的折痕条数为条,
第3次对折后的折痕条数为条,
第4次对折后的折痕条数为条,
归纳类推得:第n次对折后的折痕条数为条,
因为,
所以对折7次后折痕会超过100条;
(3)由(2)已得:对折n次后的折痕条数为条.
答案第1页,共2页
答案第1页,共2页
3.1用字母表示数-同步练习
时间:60分钟
一、单选题
1.苹果原价是每千克a元,现在按八折出售,假如现在要买,那么需要付费(
)
A.元
B.元
C.元
D.元
2.如图,则第n个图形中三角形的个数是(
)
……
第1个
第2个
第3个
A.
B.
C.
D.4n
3.书店里有x本书,第一天卖出了全部的,第二天卖出了余下的,还剩(
)本书.(
)
A.
B.
C.
D.
4.十位数字是a,个位数字比十位数字的2倍少6,百位数字比十位数字大3,这个三位数是(
).
A.
B.
C.
D.
5.将一个正方形剪成个小正方形,第一次操作按照图1所示,分割出4个正方形.第二次操作按如图2所示,分割出6个正方形,第三次操作按如图3所示,按照上述规律,则第次操作,正方形的个数为(
)
A.
B.
C.
D.
6.一根长的绳子,第一次剪去绳子的,第二次剪去剩下绳子的,如此剪下去,第100次剪完后剩下绳子的长度是(
)
A.
B.
C.
D.
7.下列说法正确的是(
)
A.-a一定是负数
B.a的倒数是
C.一定是分数
D.a2一定是非负数
8.某人骑自行车t(小时)走了,若步行,则比骑自行车多用3(小时),那么骑自行车每小时比步行多走(
).
A.
B.
C.
D.
二、填空题
9.一个没有关紧的水龙头一天滴水约0.09
m3,n个这样的水龙头一天滴水约____m3.
10.某音像社对外出租光盘的收费方法是:每张光盘在租出后的头两天每天收0.80元,以后每天收0.50元.那么一张光盘在租出n天(n是大于2的自然数)应收租金___元.
11.七年级2班要添置新桌椅,使每人有一套桌椅,共有n列,其中有一列7人,其余各列每列6人,需______套桌椅,当时,共需_______套桌椅.
12.每于克x元的糖果a千克和每千克y元的糖果b千克混合后,要求总价额不变,那么混合糖果的售价定为每千克_______元.
13.实验中学初三年级12个班中共有团员a人,则表示的实际意义是_________.
14.图中阴影部分的面积为__________.
15.如图是用棋子摆成的“上”字:如果按照以下规律继续摆下去,第n个“上”字需用______枚棋子.
16.礼堂第一排有
个座位,后面每排都比第一排多
个座位,则第
排座位有________________.
三、解答题
17.如图所示,有一块长为a,宽为b的长方形铝片,四角各截去一个边长为x的正方形,折起来做成一个没有盖的盒子.请你求盒子的容积V.
18.王刚同学拟了一张招领启事:“今天拾到钱包一个,内有人民币8.5元,请失主到一(1)班认领”.你认为这个启事合理吗?如果不合理,问题在哪里?请你改正过来.
19.小明坐计程车,发现:
请用x表示y.
20.一种长方形餐桌的四周可坐6人用餐,现把若干张这样的餐桌按如图方式进行拼接.
(1)若把4张、8张这样的餐桌拼接起来,四周分别可坐多少人?
(2)若用餐的人数有90人,则这样的餐桌需要多少张?
21.某音像公司对外出租学习光盘的收费方法是:每张光盘出租后的前2天共收费0.8元,以后每天收费0.3元.
(1)一张光盘在出租4天后共收费多少元?
(2)一张光盘在出租n(n>2且为整数)天后共收费多少元?
22.工程队计划每天修路a米,20天可以修完,实际只用了15天,实际每天修路多少米?
(1)用式子表示实际每天修路是多少米?
(2)根据多个式子,求时,实际每天修路多少米?
23.将一个长方形纸片连续对折,对折的次数越多,折痕的条数也就越多,如第一次对折后,有1条折痕,第2次对折后,共有3条折痕.
(1)第3次对折后共有多少条折痕?第4次对折后呢?
(2)对折多少次后折痕会超过100条?
(3)请找出折痕条数与对折次数的对应规律,写出对折n次后,折痕有多少条?
试卷第1页,共3页
参考答案
1.A
【解析】解:苹果原价是每千克a元,现在按八折出售,那么现价为,
∴根据“质量×单价=支付费用”可知需要付费为(元).
故选A.
2.D
【解析】由图可知:第1个图形的三角形个数为4个;
第2个图形的三角形个数为8个;
第3个图形的三角形个数为12个
…
∴第n个图形的三角形个数为4n个;
故选D.
3.D
【解析】解:∵书店有书x本,第一天卖出了全部的,
∴第一天还余下(x x)本,
∵第二天卖出了余下的,
∴还剩下x
x
(x x)本;
故选D.
4.A
【解析】解:∵十位数字是a,个位数字比十位数字的2倍少6,百位数字比十位数字大3,
∴个位数字为,百位数字为
,
∴这个三位数为
,
故选A.
5.D
【解析】解:图1分割出1+1+2×1=4个正方形,
图2分割出1+1+2×2=6个正方形,
图3分割出1+1+2×3=8个正方形,
…
则第n次操作,正方形的个数为1+1+2n=2n+2,
故选:D.
6.C
【解析】∵第一次剪去绳子的
,还剩
原长
第二次剪去剩下绳子的
,还剩
上次剩下的长度
因此每次减绳子后的长度都是上次剩下长度的
根据乘方的定义,我们得出第n次剪去绳子的
,还剩
第100次剪去绳子的
,还剩
故答案为:C.
7.D
【解析】A、当a是负数时,-a是正数,故本选项错误;
B、当a是0时,a没有倒数,故本选项错误;
C、当a=4时,
=2,是整数,故本选项错误;
D、
一定是非负数,本选项正确,
故选D.
8.B
【解析】骑自行车的速度为:
步行速度为:
骑自行车比步行每小时快出的路程:.
故选B
9.0.09n
【解析】一个没有关紧的水龙头一天滴水约0.09
m3,n个这样的水龙头一天滴水约0.09n
m3,
故答案为:0.09n.
10.0.5n+0.6
【解析】由题意可得,应收租金为:
=1.6+0.5n-1
=0.5n+0.6
故答案为0.5n+0.6
11.
37
【解析】总人数为7 +(n - 1)× 6 = 人,
桌椅数为套,
当时,6n+ 1 = 6×6+1 = 37套,
故答案为:;37.
12.
【解析】∵每于克x元的糖果a千克和每千克y元的糖果b千克,
∴总价格,
∴混合糖果的售价定为.
故答案是.
13.平均每班团员数
【解析】解:表示的实际意义是平均每班团员数.
故答案为平均每班团员数.
14.
【解析】设三个三角形的底分别为,,,则,
由图可知:
;
故答案是:.
15.(4n+2).
【解析】解:∵第一个“上”字需用6枚棋子,第二个“上”字需用10枚棋子,第三个“上”字需用14枚棋子,
∴依次多4个
∴第n个“上”字需用(4n+2)枚棋子.
故答案为:(4n+2).
16.
【解析】解:∵第一排有
个座位,
∴第2排的座位为a+1,
第3排的座位数为a+2,
…
第n排座位有
(a+n-1)个.
故答案为:(a+n-1).
17.
【解析】解:将这块铝片折成盒子后,盒子的形状为长方体,其底面是一个长为,宽为的长方形,盒子的高为x,
所以,盒子的容积.
18.不合理
【解析】解:不合理,问题出在8.5元上,应该写为n元.
19.y=5+.
【解析】由题意得,y=5+.
20.(1)4张长方形餐桌的四周可坐18人,8张长方形餐桌的四周可坐34人;(2)这样的餐桌需要22张.
【解析】解:(1)根据图中的规律可得:
当n=4时,4n+2=4×4+2=18(人);
当n=8时,4n+2=4×8+2=34(人),
答:当4张餐桌拼在一起时,可以坐18人;当8张餐桌拼在一起时,可以坐标34人;
(2)因为用餐的人数是90人,
根据题意可得:4n+2=90,
解得:n=22,
答:需要22张餐桌.
21.(1)1.4元;(2)(0.3n+0.2)元
【解析】解:(1)0.8+0.3×(4-2)=0.8+0.6=1.4(元)
答:一张光盘在出租4天后共收费1.4元;
(2)0.8+0.3(n-2)=(0.3n+0.2)元
答:一张光盘在出租n(n>2且为整数)天后共收费(0.3n+0.2)元.
22.(1)20a÷15(2)320米
【解析】(1)∵路的总长度为20a米,
∴实际每天修路的长度为20a÷15米.
答:实际每天修路的长度为20a÷15米.
(2)把a=240代入20a÷15得,
20a÷15=20×240÷15=320(米).
答:实际每天修路320米.
23.(1)第3次对折后共有7条折痕,第4次对折后有15条折痕;(2)对折7次后折痕会超过100条;(3)对折n次后,折痕有条.
【解析】(1)动手操作可知,第3次对折后的折痕条数为7条,
第4次对折后的折痕条数为15条;
(2)观察可知,第1次对折后的折痕条数为条,
第2次对折后的折痕条数为条,
第3次对折后的折痕条数为条,
第4次对折后的折痕条数为条,
归纳类推得:第n次对折后的折痕条数为条,
因为,
所以对折7次后折痕会超过100条;
(3)由(2)已得:对折n次后的折痕条数为条.
答案第1页,共2页
答案第1页,共2页
同课章节目录
- 第一章 有理数
- 1.1 正数和负数
- 1.2 数轴
- 1.3 绝对值与相反数
- 1.4 有理数的大小
- 1.5 有理数的加法
- 1.6 有理数的减法
- 1.7 有理数的加减混合运算
- 1.8 有理数的乘法
- 1.9 有理数的除法
- 1.10 有理数的乘方
- 1.11 有理数的混合运算
- 1.12 计算器的使用
- 第二章 几何图形的初步认识
- 2.1 从生活中认识几何图形
- 2.2 点和线
- 2.3 线段长短的比较
- 2.4 线段的和与差
- 2.5 角以及角的度量
- 2.6 角的大小
- 2.7 角的和与差
- 2.8 平面图形的旋转
- 第三章 代数式
- 3.1 用字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 第四章 整式的加减
- 4.1 整式
- 4.2 合并同类项
- 4.3 去括号
- 4.4 整式的加减
- 第五章 一元一次方程
- 5.1一元一次方程
- 5.2 等式的基本性质
- 5.3 解一元一次方程
- 5.4 一元一次方程的应用
