2021-2022学年鲁教版(五四制)七年级数学上册轴对称最短路径问题 专题突破训练 (word版含答案)
文档属性
| 名称 | 2021-2022学年鲁教版(五四制)七年级数学上册轴对称最短路径问题 专题突破训练 (word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 246.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-04 09:43:46 | ||
图片预览




文档简介
2021-2022学年鲁教版七年级数学上册《轴对称最短路径问题》专题突破训练(附答案)
一.选择题
1.如图,在△ABC中,AC=BC=8,∠ACB=120°,BD平分∠ABC交AC于点D,点E、F分别是线段BD,BC上的动点,则CE+EF的最小值是( )
A.2
B.4
C.5
D.6
2.如图,等腰△ABC的底边BC长为6,腰长为8,EF垂直平分AB,点P为直线EF上一动点,则BP+CP的最小值( )
A.6
B.8
C.10
D.14
3.如图,∠AOB=20°,点M、N分别是边OA、OB上的定点,点P、Q分别是OB、OA上的动点,记∠MPQ=α,∠PQN=β,当MP+PQ+QN最小时,则β﹣α的值为( )
A.10o
B.20o
C.40o
D.50o
4.如图,在△ABC中,AB的垂直平分线EF分别交AB、AC边于点E、F,点K为EF上一动点,则BK+CK的最小值是以下哪条线段的长度( )
A.EF
B.AB
C.AC
D.BC
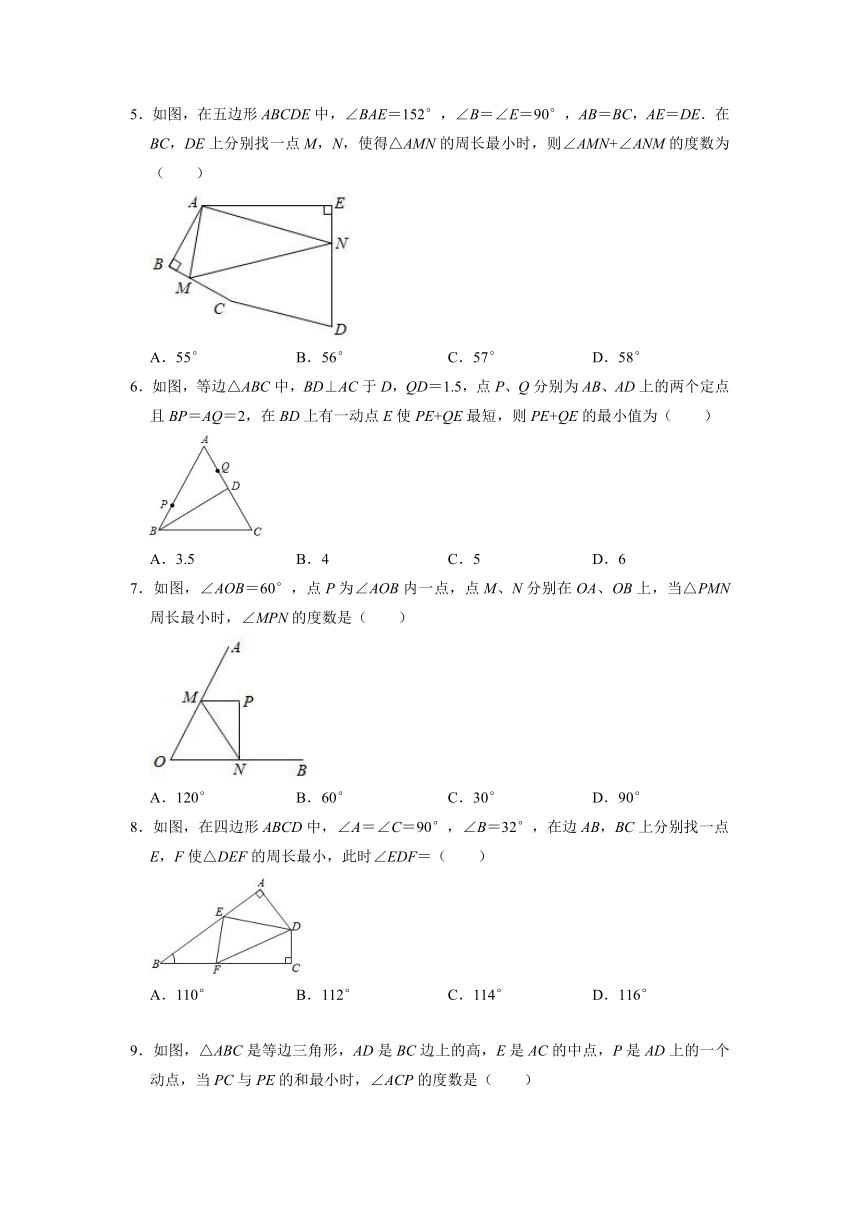
5.如图,在五边形ABCDE中,∠BAE=152°,∠B=∠E=90°,AB=BC,AE=DE.在BC,DE上分别找一点M,N,使得△AMN的周长最小时,则∠AMN+∠ANM的度数为( )
A.55°
B.56°
C.57°
D.58°
6.如图,等边△ABC中,BD⊥AC于D,QD=1.5,点P、Q分别为AB、AD上的两个定点且BP=AQ=2,在BD上有一动点E使PE+QE最短,则PE+QE的最小值为( )
A.3.5
B.4
C.5
D.6
7.如图,∠AOB=60°,点P为∠AOB内一点,点M、N分别在OA、OB上,当△PMN周长最小时,∠MPN的度数是( )
A.120°
B.60°
C.30°
D.90°
8.如图,在四边形ABCD中,∠A=∠C=90°,∠B=32°,在边AB,BC上分别找一点E,F使△DEF的周长最小,此时∠EDF=( )
A.110°
B.112°
C.114°
D.116°
9.如图,△ABC是等边三角形,AD是BC边上的高,E是AC的中点,P是AD上的一个动点,当PC与PE的和最小时,∠ACP的度数是( )
A.30°
B.45°
C.60°
D.90°
10.如图,等腰三角形ABC的底边BC为4,面积为24,腰AC的垂直平分线EF分别交边AC,AB于点E,F,若D为BC边的中点,M为线段EF上一动点,则△CDM的周长的最小值为( )
A.8
B.10
C.12
D.14
13.如图,在△ABC中,∠BAC=68°,∠C=36°,AD平分∠BAC,M、N分别是AD、AB上的动点,当BM+MN最小时,∠BMN的度数为( )
A.34°
B.68°
C.76°
D.90°
二.填空题
12.如图,在△ABC中,AB=6,BC=7,AC=4,直线m是△ABC中BC边的垂直平分线,P是直线m上的一动点,则△APC的周长的最小值为
.
13.如图,点P是∠AOB内任意一点,OP=5cm,点M和点N分别是射线OA和射线OB上的动点,△PMN周长的最小值是5cm,则∠AOB的度数是
.
14.如图,∠AOB=30°,点M、N分别是射线OB、OA上的动点,点P为∠AOB内一点,且OP=8,则△PMN的周长的最小值=
.
15.如图,点C,D分别是边∠AOB两边OA、OB上的定点,∠AOB=20°,OC=OD=4.点E,F分别是边OB,OA上的动点,则CE+EF+FD的最小值是
.
三.解答题
16.如图,∠XOY内有一点P,在射线OX上找出一点M,在射线OY上找出一点N,使PM+MN+NP最短.
17.如图,已知两点P、Q在锐角∠AOB内,分别在OA、OB上求作点M、N,使PM+MN+NQ最短.
18.如图1和图2,P是直线m上一动点,A、B两点在直线m的同侧,且点A、B所在直线与m不平行.
(1)当P点运动到P1位置时,距离A点最近,在图1中的直线m上画出点P1的位置;
(2)当P点运动到P2位置时,与A点的距离和与B点距两相等,请在图2中作出P2位置;
(3)在直线m上是否存在这样一点P3,使得到A点的距离与到B点的距离之和最小?若存在请在图3中作出这点,若不存在清说明理由.(要求:不写作法,请保留作图痕迹)
19.如图,在所给网格图(每小格均为边长是1的正方形)中完成下列各题:(用直尺画图)
(1)画出格点△ABC(顶点均在格点上)关于直线DE对称的
△A1B1C1;
(2)在DE上画出点Q,使△QAC的周长最小.
20.如图,在正方形网格上的一个△ABC.(其中点A、B、C均在网格上)
(1)作△ABC关于直线MN的轴对称图形△A′B′C′;
(2)以P点为一个顶点作一个与△ABC全等的△EPF(规定点P与点B对应,另两顶点都在图中网格交点处).
(3)在MN上画出点Q,使得QA+QC最小.
参考答案
1.解:作C点关于BD的对称点C',过C'作C'F⊥BC交BD于点E,交BC于点F,
∴CE+EF=C'E+EF≥C'F,
∴CE+EF的最小值C'F的长,
∴CC'⊥BD,
∵BD平分∠ABC,
∴∠C'BG=∠GBC,
在△C'BG和△CBG中,
,
∴△C'BG≌△CBG(ASA),
∴BC=BC',
∵AC=BC=8,∠ACB=120°,
∴∠ABC=30°,BC'=8,
在Rt△BCC'中,C'F=4,
∴CE+EF的最小值为4,
故选:B.
2.解:连接AP,
∵EF垂直平分AB,
∴AP=BP,
∴BP+CP≥AC,
∴当PB+CP=AC时,BP+CP值最小,
∵等腰△ABC腰长为8,
∴AC=8,
∴BP+CP的最小值为8,故选:B.
3.解:如图,作M关于OB的对称点M′,N关于OA的对称点N′,连接M′N′交OA于Q,交OB于P,则MP+PQ+QN最小,
∴∠OPM=∠OPM′=∠NPQ,∠OQP=∠AQN′=∠AQN,
∴∠QPN=(180°﹣α)=∠AOB+∠MQP=20°+(180°﹣β),
∴180°﹣α=40°+(180°﹣β),
∴β﹣α=40°,
故选:C.
4.解:连接AK,
∵EF是线段AB的垂直平分线,
∴AK=BK,
∴BK+CK=AK+CK,
∴AK+CK的最小值=BK+CK的最小值,
∵AK+CK≥AC,
∴当AK+CK=AC时,AK+CK的值最小,即BK+CK的值最小,
∴BK+CK的最小值是线段AC的长度,
故选:C.
5.解:如图,延长AB至A′,使A′B=AB,
延长AE至A″,使A″E=AE,
则BC垂直平分AA′,DE垂直平分AA″,
∴AM=A′M,AN=A″N,
根据两点之间,线段最短,
当A′,M,N,A″四点在一条直线时,A′M+MN+NA″最小,
则AM+MN+AN的值最小,
即△AMN的周长最小,
∵AM=A′M,AN=A″N,
∴可设∠MAA′=∠MA′A=x,∠NAA″=∠NA″A=y,
在△AA′A″中,x+y=180°﹣∠BAE=180°﹣152°=28°,
∵∠AMN=∠MAA′+∠MA′A=2x,∠ANM=2y,
∴∠AMN+∠ANM=2x+2y=56°,
故选:B.
6.解:如图,∵△ABC是等边三角形,
∴BA=BC,
∵BD⊥AC,AQ=2cm,QD=1.5cm,
∴AD=DC=AQ+QD=3.5(cm),
作点Q关于BD的对称点Q′,连接PQ′交BD于E,连接QE,此时PE+EQ的值最小.最小值PE+QE=PE+EQ′=PQ′,
∵AQ=2cm,AD=DC=3.5cm,
∴QD=DQ′=1.5(cm),
∴CQ′=BP=2(cm),
∴AP=AQ′=5(cm),
∵∠A=60°,
∴△APQ′是等边三角形,
∴PQ′=PA=5(cm),
∴PE+QE的最小值为5cm.
故选:C.
7.解:分别作点P关于OA、OB的对称点P1、P2,连接P1、P2交OA于M,交OB于N,
∴OP1=OP=OP2,∠OP1M=∠MPO,∠NPO=∠NP2O,
根据轴对称的性质可得MP=P1M,PN=P2N,
∴△PMN的周长的最小值=P1P2,
由轴对称的性质可得∠P1OP2=2∠AOB,
∴等腰△OP1P2中,∠OP1P2+∠OP2P1=180°﹣2∠P1OP2,
∴∠MPN=∠OPM+∠OPN=∠OP1M+∠OP2N=∠OP1P2+∠OP2P1=180°﹣2∠P1OP2=60°,
故选:B.
8.解:如图,作点D关于BA的对称点P,点D关于BC的对称点Q,连接PQ,交AB于E′,交BC于F′,则点E′,F′即为所求.
∵四边形ABCD中,∠A=∠C=90°,∠B=α,
∴∠ADC=180°﹣α,
由轴对称知,∠ADE′=∠P,∠CDF′=∠Q,
在△PDQ中,∠P+∠Q=180°﹣∠ADC
=180°﹣(180°﹣32°)
=32°,
∴∠ADE′+∠CDF′=∠P+∠Q=32°,
∴∠E′DF′=∠ADC﹣(∠ADE′+∠CDF′)
=180°﹣64°
=116°.
故选:D.
9.解:如图,连接BE,与AD交于点P,此时PE+PC最小,
∵△ABC是等边三角形,AD⊥BC,
∴PC=PB,
∴PE+PC=PB+PE≥BE,
即BE就是PE+PC的最小值,
∵△ABC是等边三角形,
∴∠BCE=60°,
∵BA=BC,AE=EC,
∴BE⊥AC,
∴∠BEC=90°,
∴∠EBC=30°,
∵PB=PC,
∴∠PCB=∠PBC=30°,
∴∠ACP=30°,
故选:A.
10.解:连接AD,MA.
∵△ABC是等腰三角形,点D是BC边的中点,
∴AD⊥BC,
∴S△ABC=BC AD=×4×AD=24,解得AD=12,
∵EF是线段AC的垂直平分线,
∴点A关于直线EF的对称点为点C,MA=MC,
∴MC+DM=MA+DM≥AD,
∴AD的长为CM+MD的最小值,
∴△CDM的周长最短=(CM+MD)+CD=AD+BC=12+×4=14.
故选:D.
11.解:∵∠BAC=68°,∠C=36°,
∴∠ABC=180°﹣68°﹣36°=76°,
如图,过B作BE⊥AC于E,交AD于M,
在AB上截取AN=AE,连接MN,
∵∠BAC的平分线交BC于点D,
∴∠EAM=∠NAM,
在△AME与△AMN中,
,
∴△AME≌△AMN(SAS),
∴ME=MN.∠ANM=∠AEM,
∴BM+MN=BM+ME=BE,
BM+MN最小值,只要求BM+EM的最小值,
当BE⊥AC时,BM+ME最小,
此时∠ABE=90°﹣68°=22°,
∴∠ANM=90°,
∴∠BMN=90°﹣22°=68°
故选:B.
12.解:∵直线m是△ABC中BC边的垂直平分线,
∴BP=CP,
∴△ACP的周长=AP+PC+AC=BP+AP+AC≥AB+AC,
∴当A、B、P三点共线时,△ACP的周长最小,
∵AB=6,BC=7,AC=4,
∴△ACP的周长6+4=10,
∴△ACP的周长最小值为10,
故答案为10.
13.解:分别作点P关于OA、OB的对称点D、C,连接CD,
分别交OA、OB于点M、N,连接OC、OD、PM、PN、MN,如图所示:
∵点P关于OA的对称点为D,关于OB的对称点为C,
∴PM=DM,OP=OD,∠DOA=∠POA;
∵点P关于OB的对称点为C,
∴PN=CN,OP=OC,∠COB=∠POB,
∴OC=OP=OD,∠AOB=∠COD,
∵△PMN周长的最小值是5cm,
∴PM+PN+MN=5,
∴DM+CN+MN=5,
即CD=5=OP,
∴OC=OD=CD,
即△OCD是等边三角形,
∴∠COD=60°,
∴∠AOB=30°;
故答案为30°.
14.解:分别作点P关于OA、OB的对称点C、D,连接CD,分别交OA、OB于点M、N,连接OP、OC、OD、PM、PN.
∵点P关于OA的对称点为C,关于OB的对称点为D,
∴PM=CM,OP=OC,∠COA=∠POA;
∵点P关于OB的对称点为D,
∴PN=DN,OP=OD,∠DOB=∠POB,
∴OC=OD=OP=8cm,∠COD=∠COA+∠POA+∠POB+∠DOB=2∠POA+2∠POB=2∠AOB=60°,
∴△COD是等边三角形,
∴CD=OC=OD=8.
∴△PMN的周长的最小值=PM+MN+PN=CM+MN+DN≥CD=8.
故答案为:8.
15.解:作C关于OB的对称点C′,作D关于OA的对称点D′,
连接C′D′,即为CE+EF+FD的最小值.
根据轴对称的定义可知:∠DOC′=∠AOB=∠FOD′=20°,
∴△OC′D′为等边三角形
∴C′D′=OC′=OC=4.
故答案为4.
16.解:如图所示:分别以直线OX、OY为对称轴,作点P的对应点P1与P2,
连接P1P2交OX于M,交OY于N,
则PM+MN+NP最短.
17.解:如图所示.
18.解:(1)过点A作直线m的垂线,垂足为P1,
则P1即为所求;
(2)作线段AB的垂直平分线交直线m于P2,
则P2即为所求;
(3)作点A关于直线m对称点A′,连接BA′交直线m于P3,
则P3即为所求.
19.解:(1)所作图形如图所示:
(2)如图所示:
利用轴对称图形的性质可得点C关于直线DE的对称点C1,
连接AC1,交直线DE于点Q,点
Q即为所求,此时△QAC的周长最小.
20.解:(1)如右图所示,△A′B′C′即为所求;
(2)如右图所示,△EPF即为所求;
(3)如右图所示,线段AC′于MN的交点Q即为所求.
一.选择题
1.如图,在△ABC中,AC=BC=8,∠ACB=120°,BD平分∠ABC交AC于点D,点E、F分别是线段BD,BC上的动点,则CE+EF的最小值是( )
A.2
B.4
C.5
D.6
2.如图,等腰△ABC的底边BC长为6,腰长为8,EF垂直平分AB,点P为直线EF上一动点,则BP+CP的最小值( )
A.6
B.8
C.10
D.14
3.如图,∠AOB=20°,点M、N分别是边OA、OB上的定点,点P、Q分别是OB、OA上的动点,记∠MPQ=α,∠PQN=β,当MP+PQ+QN最小时,则β﹣α的值为( )
A.10o
B.20o
C.40o
D.50o
4.如图,在△ABC中,AB的垂直平分线EF分别交AB、AC边于点E、F,点K为EF上一动点,则BK+CK的最小值是以下哪条线段的长度( )
A.EF
B.AB
C.AC
D.BC
5.如图,在五边形ABCDE中,∠BAE=152°,∠B=∠E=90°,AB=BC,AE=DE.在BC,DE上分别找一点M,N,使得△AMN的周长最小时,则∠AMN+∠ANM的度数为( )
A.55°
B.56°
C.57°
D.58°
6.如图,等边△ABC中,BD⊥AC于D,QD=1.5,点P、Q分别为AB、AD上的两个定点且BP=AQ=2,在BD上有一动点E使PE+QE最短,则PE+QE的最小值为( )
A.3.5
B.4
C.5
D.6
7.如图,∠AOB=60°,点P为∠AOB内一点,点M、N分别在OA、OB上,当△PMN周长最小时,∠MPN的度数是( )
A.120°
B.60°
C.30°
D.90°
8.如图,在四边形ABCD中,∠A=∠C=90°,∠B=32°,在边AB,BC上分别找一点E,F使△DEF的周长最小,此时∠EDF=( )
A.110°
B.112°
C.114°
D.116°
9.如图,△ABC是等边三角形,AD是BC边上的高,E是AC的中点,P是AD上的一个动点,当PC与PE的和最小时,∠ACP的度数是( )
A.30°
B.45°
C.60°
D.90°
10.如图,等腰三角形ABC的底边BC为4,面积为24,腰AC的垂直平分线EF分别交边AC,AB于点E,F,若D为BC边的中点,M为线段EF上一动点,则△CDM的周长的最小值为( )
A.8
B.10
C.12
D.14
13.如图,在△ABC中,∠BAC=68°,∠C=36°,AD平分∠BAC,M、N分别是AD、AB上的动点,当BM+MN最小时,∠BMN的度数为( )
A.34°
B.68°
C.76°
D.90°
二.填空题
12.如图,在△ABC中,AB=6,BC=7,AC=4,直线m是△ABC中BC边的垂直平分线,P是直线m上的一动点,则△APC的周长的最小值为
.
13.如图,点P是∠AOB内任意一点,OP=5cm,点M和点N分别是射线OA和射线OB上的动点,△PMN周长的最小值是5cm,则∠AOB的度数是
.
14.如图,∠AOB=30°,点M、N分别是射线OB、OA上的动点,点P为∠AOB内一点,且OP=8,则△PMN的周长的最小值=
.
15.如图,点C,D分别是边∠AOB两边OA、OB上的定点,∠AOB=20°,OC=OD=4.点E,F分别是边OB,OA上的动点,则CE+EF+FD的最小值是
.
三.解答题
16.如图,∠XOY内有一点P,在射线OX上找出一点M,在射线OY上找出一点N,使PM+MN+NP最短.
17.如图,已知两点P、Q在锐角∠AOB内,分别在OA、OB上求作点M、N,使PM+MN+NQ最短.
18.如图1和图2,P是直线m上一动点,A、B两点在直线m的同侧,且点A、B所在直线与m不平行.
(1)当P点运动到P1位置时,距离A点最近,在图1中的直线m上画出点P1的位置;
(2)当P点运动到P2位置时,与A点的距离和与B点距两相等,请在图2中作出P2位置;
(3)在直线m上是否存在这样一点P3,使得到A点的距离与到B点的距离之和最小?若存在请在图3中作出这点,若不存在清说明理由.(要求:不写作法,请保留作图痕迹)
19.如图,在所给网格图(每小格均为边长是1的正方形)中完成下列各题:(用直尺画图)
(1)画出格点△ABC(顶点均在格点上)关于直线DE对称的
△A1B1C1;
(2)在DE上画出点Q,使△QAC的周长最小.
20.如图,在正方形网格上的一个△ABC.(其中点A、B、C均在网格上)
(1)作△ABC关于直线MN的轴对称图形△A′B′C′;
(2)以P点为一个顶点作一个与△ABC全等的△EPF(规定点P与点B对应,另两顶点都在图中网格交点处).
(3)在MN上画出点Q,使得QA+QC最小.
参考答案
1.解:作C点关于BD的对称点C',过C'作C'F⊥BC交BD于点E,交BC于点F,
∴CE+EF=C'E+EF≥C'F,
∴CE+EF的最小值C'F的长,
∴CC'⊥BD,
∵BD平分∠ABC,
∴∠C'BG=∠GBC,
在△C'BG和△CBG中,
,
∴△C'BG≌△CBG(ASA),
∴BC=BC',
∵AC=BC=8,∠ACB=120°,
∴∠ABC=30°,BC'=8,
在Rt△BCC'中,C'F=4,
∴CE+EF的最小值为4,
故选:B.
2.解:连接AP,
∵EF垂直平分AB,
∴AP=BP,
∴BP+CP≥AC,
∴当PB+CP=AC时,BP+CP值最小,
∵等腰△ABC腰长为8,
∴AC=8,
∴BP+CP的最小值为8,故选:B.
3.解:如图,作M关于OB的对称点M′,N关于OA的对称点N′,连接M′N′交OA于Q,交OB于P,则MP+PQ+QN最小,
∴∠OPM=∠OPM′=∠NPQ,∠OQP=∠AQN′=∠AQN,
∴∠QPN=(180°﹣α)=∠AOB+∠MQP=20°+(180°﹣β),
∴180°﹣α=40°+(180°﹣β),
∴β﹣α=40°,
故选:C.
4.解:连接AK,
∵EF是线段AB的垂直平分线,
∴AK=BK,
∴BK+CK=AK+CK,
∴AK+CK的最小值=BK+CK的最小值,
∵AK+CK≥AC,
∴当AK+CK=AC时,AK+CK的值最小,即BK+CK的值最小,
∴BK+CK的最小值是线段AC的长度,
故选:C.
5.解:如图,延长AB至A′,使A′B=AB,
延长AE至A″,使A″E=AE,
则BC垂直平分AA′,DE垂直平分AA″,
∴AM=A′M,AN=A″N,
根据两点之间,线段最短,
当A′,M,N,A″四点在一条直线时,A′M+MN+NA″最小,
则AM+MN+AN的值最小,
即△AMN的周长最小,
∵AM=A′M,AN=A″N,
∴可设∠MAA′=∠MA′A=x,∠NAA″=∠NA″A=y,
在△AA′A″中,x+y=180°﹣∠BAE=180°﹣152°=28°,
∵∠AMN=∠MAA′+∠MA′A=2x,∠ANM=2y,
∴∠AMN+∠ANM=2x+2y=56°,
故选:B.
6.解:如图,∵△ABC是等边三角形,
∴BA=BC,
∵BD⊥AC,AQ=2cm,QD=1.5cm,
∴AD=DC=AQ+QD=3.5(cm),
作点Q关于BD的对称点Q′,连接PQ′交BD于E,连接QE,此时PE+EQ的值最小.最小值PE+QE=PE+EQ′=PQ′,
∵AQ=2cm,AD=DC=3.5cm,
∴QD=DQ′=1.5(cm),
∴CQ′=BP=2(cm),
∴AP=AQ′=5(cm),
∵∠A=60°,
∴△APQ′是等边三角形,
∴PQ′=PA=5(cm),
∴PE+QE的最小值为5cm.
故选:C.
7.解:分别作点P关于OA、OB的对称点P1、P2,连接P1、P2交OA于M,交OB于N,
∴OP1=OP=OP2,∠OP1M=∠MPO,∠NPO=∠NP2O,
根据轴对称的性质可得MP=P1M,PN=P2N,
∴△PMN的周长的最小值=P1P2,
由轴对称的性质可得∠P1OP2=2∠AOB,
∴等腰△OP1P2中,∠OP1P2+∠OP2P1=180°﹣2∠P1OP2,
∴∠MPN=∠OPM+∠OPN=∠OP1M+∠OP2N=∠OP1P2+∠OP2P1=180°﹣2∠P1OP2=60°,
故选:B.
8.解:如图,作点D关于BA的对称点P,点D关于BC的对称点Q,连接PQ,交AB于E′,交BC于F′,则点E′,F′即为所求.
∵四边形ABCD中,∠A=∠C=90°,∠B=α,
∴∠ADC=180°﹣α,
由轴对称知,∠ADE′=∠P,∠CDF′=∠Q,
在△PDQ中,∠P+∠Q=180°﹣∠ADC
=180°﹣(180°﹣32°)
=32°,
∴∠ADE′+∠CDF′=∠P+∠Q=32°,
∴∠E′DF′=∠ADC﹣(∠ADE′+∠CDF′)
=180°﹣64°
=116°.
故选:D.
9.解:如图,连接BE,与AD交于点P,此时PE+PC最小,
∵△ABC是等边三角形,AD⊥BC,
∴PC=PB,
∴PE+PC=PB+PE≥BE,
即BE就是PE+PC的最小值,
∵△ABC是等边三角形,
∴∠BCE=60°,
∵BA=BC,AE=EC,
∴BE⊥AC,
∴∠BEC=90°,
∴∠EBC=30°,
∵PB=PC,
∴∠PCB=∠PBC=30°,
∴∠ACP=30°,
故选:A.
10.解:连接AD,MA.
∵△ABC是等腰三角形,点D是BC边的中点,
∴AD⊥BC,
∴S△ABC=BC AD=×4×AD=24,解得AD=12,
∵EF是线段AC的垂直平分线,
∴点A关于直线EF的对称点为点C,MA=MC,
∴MC+DM=MA+DM≥AD,
∴AD的长为CM+MD的最小值,
∴△CDM的周长最短=(CM+MD)+CD=AD+BC=12+×4=14.
故选:D.
11.解:∵∠BAC=68°,∠C=36°,
∴∠ABC=180°﹣68°﹣36°=76°,
如图,过B作BE⊥AC于E,交AD于M,
在AB上截取AN=AE,连接MN,
∵∠BAC的平分线交BC于点D,
∴∠EAM=∠NAM,
在△AME与△AMN中,
,
∴△AME≌△AMN(SAS),
∴ME=MN.∠ANM=∠AEM,
∴BM+MN=BM+ME=BE,
BM+MN最小值,只要求BM+EM的最小值,
当BE⊥AC时,BM+ME最小,
此时∠ABE=90°﹣68°=22°,
∴∠ANM=90°,
∴∠BMN=90°﹣22°=68°
故选:B.
12.解:∵直线m是△ABC中BC边的垂直平分线,
∴BP=CP,
∴△ACP的周长=AP+PC+AC=BP+AP+AC≥AB+AC,
∴当A、B、P三点共线时,△ACP的周长最小,
∵AB=6,BC=7,AC=4,
∴△ACP的周长6+4=10,
∴△ACP的周长最小值为10,
故答案为10.
13.解:分别作点P关于OA、OB的对称点D、C,连接CD,
分别交OA、OB于点M、N,连接OC、OD、PM、PN、MN,如图所示:
∵点P关于OA的对称点为D,关于OB的对称点为C,
∴PM=DM,OP=OD,∠DOA=∠POA;
∵点P关于OB的对称点为C,
∴PN=CN,OP=OC,∠COB=∠POB,
∴OC=OP=OD,∠AOB=∠COD,
∵△PMN周长的最小值是5cm,
∴PM+PN+MN=5,
∴DM+CN+MN=5,
即CD=5=OP,
∴OC=OD=CD,
即△OCD是等边三角形,
∴∠COD=60°,
∴∠AOB=30°;
故答案为30°.
14.解:分别作点P关于OA、OB的对称点C、D,连接CD,分别交OA、OB于点M、N,连接OP、OC、OD、PM、PN.
∵点P关于OA的对称点为C,关于OB的对称点为D,
∴PM=CM,OP=OC,∠COA=∠POA;
∵点P关于OB的对称点为D,
∴PN=DN,OP=OD,∠DOB=∠POB,
∴OC=OD=OP=8cm,∠COD=∠COA+∠POA+∠POB+∠DOB=2∠POA+2∠POB=2∠AOB=60°,
∴△COD是等边三角形,
∴CD=OC=OD=8.
∴△PMN的周长的最小值=PM+MN+PN=CM+MN+DN≥CD=8.
故答案为:8.
15.解:作C关于OB的对称点C′,作D关于OA的对称点D′,
连接C′D′,即为CE+EF+FD的最小值.
根据轴对称的定义可知:∠DOC′=∠AOB=∠FOD′=20°,
∴△OC′D′为等边三角形
∴C′D′=OC′=OC=4.
故答案为4.
16.解:如图所示:分别以直线OX、OY为对称轴,作点P的对应点P1与P2,
连接P1P2交OX于M,交OY于N,
则PM+MN+NP最短.
17.解:如图所示.
18.解:(1)过点A作直线m的垂线,垂足为P1,
则P1即为所求;
(2)作线段AB的垂直平分线交直线m于P2,
则P2即为所求;
(3)作点A关于直线m对称点A′,连接BA′交直线m于P3,
则P3即为所求.
19.解:(1)所作图形如图所示:
(2)如图所示:
利用轴对称图形的性质可得点C关于直线DE的对称点C1,
连接AC1,交直线DE于点Q,点
Q即为所求,此时△QAC的周长最小.
20.解:(1)如右图所示,△A′B′C′即为所求;
(2)如右图所示,△EPF即为所求;
(3)如右图所示,线段AC′于MN的交点Q即为所求.
