6.5一次函数的应用同步课时作业 2021-2022学年数学鲁教版(五四制)七年级上册(word版含答案)
文档属性
| 名称 | 6.5一次函数的应用同步课时作业 2021-2022学年数学鲁教版(五四制)七年级上册(word版含答案) | 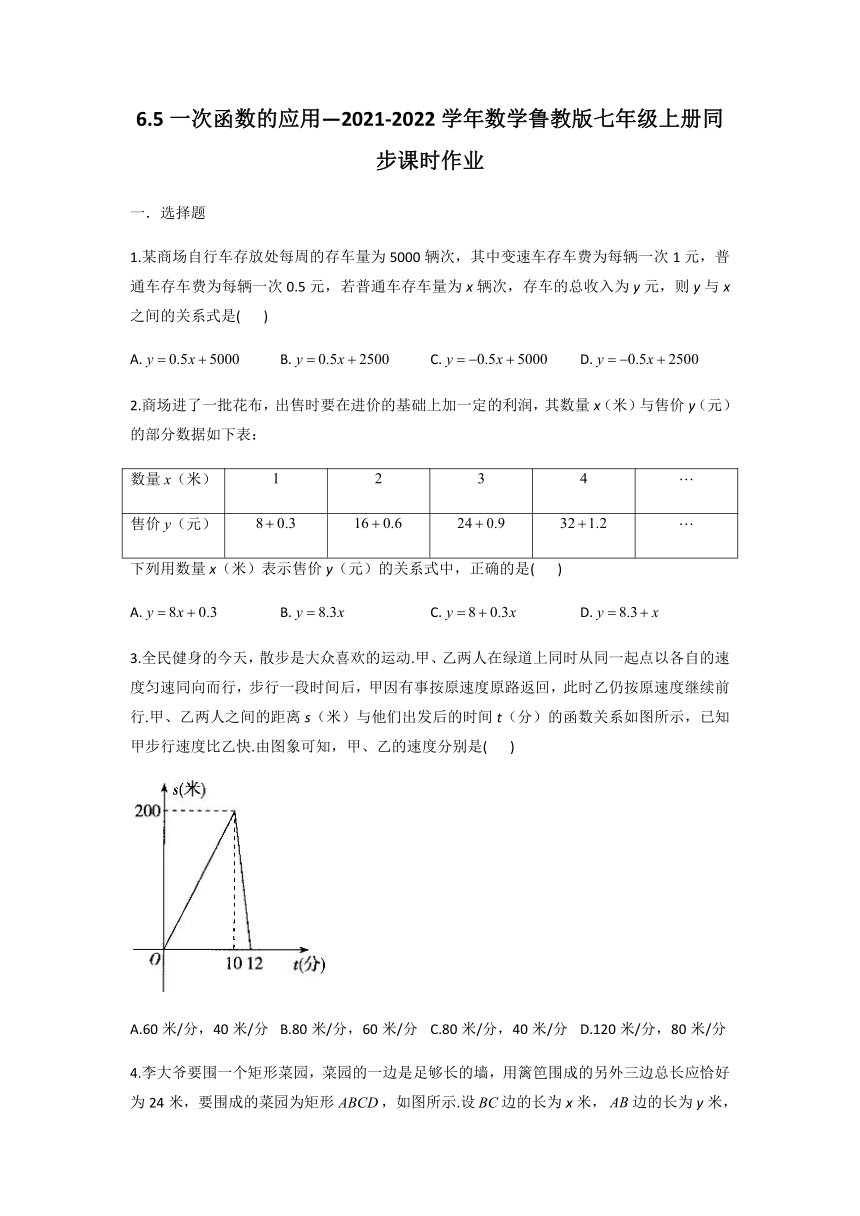 | |
| 格式 | docx | ||
| 文件大小 | 441.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-04 09:52:19 | ||
图片预览




文档简介
6.5一次函数的应用—2021-2022学年数学鲁教版七年级上册同步课时作业
一.选择题
1.某商场自行车存放处每周的存车量为5000辆次,其中变速车存车费为每辆一次1元,普通车存车费为每辆一次0.5元,若普通车存车量为x辆次,存车的总收入为y元,则y与x之间的关系式是(
)
A.
B.
C.
D.
2.商场进了一批花布,出售时要在进价的基础上加一定的利润,其数量x(米)与售价y(元)的部分数据如下表:
数量x(米)
1
2
3
4
售价y(元)
下列用数量x(米)表示售价y(元)的关系式中,正确的是(
)
A.
B.
C.
D.
3.全民健身的今天,散步是大众喜欢的运动.甲、乙两人在绿道上同时从同一起点以各自的速度匀速同向而行,步行一段时间后,甲因有事按原速度原路返回,此时乙仍按原速度继续前行.甲、乙两人之间的距离s(米)与他们出发后的时间t(分)的函数关系如图所示,已知甲步行速度比乙快.由图象可知,甲、乙的速度分别是(
)
A.60米/分,40米/分
B.80米/分,60米/分
C.80米/分,40米/分
D.120米/分,80米/分
4.李大爷要围一个矩形菜园,菜园的一边是足够长的墙,用篱笆围成的另外三边总长应恰好为24米,要围成的菜园为矩形,如图所示.设边的长为x米,边的长为y米,则y与x之间的函数关系式是(
)
A.
B.
C.
D.
5.如图,直角三角形ABC的两直角边BC、AC分别与x轴、y轴平行,且,顶点A的坐标为,若某正比例函数的图象经过点B,则此正比例函数的表达式为(
)
A.
B.
C.
D.
6.如图,一条直线与两坐标轴的正半轴分别交于两点,P是线段上任意一点(不包括端点),过点P分别作两坐标轴的垂线与两坐标轴围成的矩形的周长为8,则该直线的函数表达式是(
)
A.
B.
C.
D.
7.一个容器有进水管和出水管,每分钟的进水量和出水量是两个常数.从某时刻开始内只进水不出水,从第到第内既进水又出水,从第开始只出水不进水,容器内水量(单位:)与时间(单位:)之间的关系如图所示,则图中的值是(
)
A.32
B.34
C.36
D.38
8.某快递公司每天上午7:00—8:00为集中揽件和派件时段,甲仓库用来揽收快件,乙仓库用来派发快件,该时段内甲、乙两仓库的快件数量y(件)与时间x(分)之间的函数图象如图所示,下列说法正确的有(
)
①15分钟后,甲仓库内快件数量为180件;
②乙仓库每分钟派送快件的数量为4件;
③8:00时,甲仓库内快件数量为400件;
④7:20时,两仓库快件数量相同.
A.1个
B.2个
C.3个
D.4个
9.学校计划购买A和B两种品牌的足球,已知一个A品牌足球60元,一个B品牌足球75元,学校准备将1500元钱全部用于购买这两种足球(两种足球都买),该学校的购买方案共有(
)
A.3种
B.4种
C.5种
D.6种
二.填空题
10.我国很多城市水资源缺乏,为了加强居民的节水意识,某自来水公司采取分段收费方式,某市居民月交水费y(元)与用水量x(吨)之间的关系如图所示,若某户居民4月份用水20吨,则应交水费___________元.
11.已知金属棒的长度l(cm)是温度t(℃)的一次函数.现有一根金属棒,在0℃时的长度是200cm,温度每升高1℃,它就伸长0.002cm,则这根金属棒的长度l(cm)与温度t(℃)的函数关系式为____________.
12.学校与图书馆在同一条笔直道路上,甲从学校去图书馆,乙从图书馆回学校,甲、乙两人都匀速步行且同时出发,乙先到达目的地两人之间的距离y(米)与时间t(分)之间的函数关系如图所示,则乙到达目的地时,甲离目的地还有
米.
三.解答题
13.暑期将至,某健身俱乐部面向学生推出暑期优惠活动,活动方案如下:
方案一:购买一张学生暑期专享卡,每次健身费用按六折优惠;
方案二:不购买学生暑期专享卡,每次健身费用按八折优惠.
设某学生暑期健身x(次),按照方案一所需费用为(元),且;按照方案二所需费用为(元),且.其函数图象如图所示.
(1)求和b的值,并说明它们的实际意义;
(2)求打折前的每次健身费用和的值;
(3)八年级学生小华计划暑期前往该俱乐部健身8次,选择哪种方案所需费用更少?说明理由.
答案以及解析
1.答案:C
解析:由题意可得,故选C.
2.答案:B
解析:依题意得.故选B.
3.答案:A
解析:根据题意可知,甲每分钟比乙快:(米),设乙的速度为x米/分,则甲的速度为米/分,根据题意得,解得,,故甲的速度为60米/分,乙的速度为40米/分,故选A.
4.答案:B
解析:根据题意,得,所以,因为,所以.故选B.
5.答案:A
解析:轴,轴,,顶点A的坐标为,,设正比例函数的表达式为,,解得,正比例函数的表达式为,故选A.
6.答案:A
解析:如图,设过点P的两垂线分别与x轴,y轴的交点为.
设点P的坐标为.
点P在第一象限,.
矩形的周长为8,,.
该直线的函数表达式是.故选A.
7.答案:C
解析:由题图可知每分钟的进水量为,设每分钟的出水量为,则,解得第时,,.
8.答案:C
解析:由题意结合题图可知:
15分钟后,甲仓库内快件数量为130件,故①说法错误;
甲仓库揽收快件的速度为(件/分),
所以8:00时,甲仓库内快件数为(件),故③说法正确;
(分),即45分钟乙仓库派送快件180件,
所以乙仓库每分钟派送快件的数量为(件),故②说法正确;
所以刚开始时乙仓库快件的总数量为(件),
设x分钟后,两仓库快件数量相同,根据题意得,解得,
即7:20时,两仓库快件数量相同,故④说法正确.
所以说法正确的有②③④,共3个.故选C.
9.答案:B
解析:设购买A品牌足球x个,购买B品牌足球y个.根据题意,得.
均为正整数,
或或或
该学校共有4种购买方案.故选B.
10.答案:44
解析:由题图可知,超出10吨的部分,每吨水的价格是(元),当用水20吨时,应交水费:(元),故答案为44.
11.答案:
解析:设l与t的函数关系式为,将代入,可得.由温度每升高1℃,它就伸长0.002cm得,故金属棒的长度l(cm)与温度t(℃)的函数关系式为.
12.答案:800
解析:根据题中的图象信息知,当时,甲、乙两人相遇,甲的速度为米/分,
甲从学校去图书馆,乙从图书馆回学校,甲、乙两人都匀速步行且同时出发,
当时,甲、乙两人相遇,甲、乙两人的速度和为米/分,
乙的速度为米/分乙从图书馆回学校的时间为分钟,
乙到达目的地时,甲离目的地的距离为米.
13.答案:(1)函数图象经过点,,
.解得.
表示的实际意义是购买一张学生暑期专享卡后每次健身费用为15元,
表示的实际意义是购买一张学生暑期专享卡的费用为30元.
(2)由题意可得,折前的每次健身费用为元,
则.
(3)选择方案一所需费用更少.
理由:,.
当健身8次时,选择方案一所需费用为元;
选择方案二所需费用为元,
,选择方案一所需费用更少.
一.选择题
1.某商场自行车存放处每周的存车量为5000辆次,其中变速车存车费为每辆一次1元,普通车存车费为每辆一次0.5元,若普通车存车量为x辆次,存车的总收入为y元,则y与x之间的关系式是(
)
A.
B.
C.
D.
2.商场进了一批花布,出售时要在进价的基础上加一定的利润,其数量x(米)与售价y(元)的部分数据如下表:
数量x(米)
1
2
3
4
售价y(元)
下列用数量x(米)表示售价y(元)的关系式中,正确的是(
)
A.
B.
C.
D.
3.全民健身的今天,散步是大众喜欢的运动.甲、乙两人在绿道上同时从同一起点以各自的速度匀速同向而行,步行一段时间后,甲因有事按原速度原路返回,此时乙仍按原速度继续前行.甲、乙两人之间的距离s(米)与他们出发后的时间t(分)的函数关系如图所示,已知甲步行速度比乙快.由图象可知,甲、乙的速度分别是(
)
A.60米/分,40米/分
B.80米/分,60米/分
C.80米/分,40米/分
D.120米/分,80米/分
4.李大爷要围一个矩形菜园,菜园的一边是足够长的墙,用篱笆围成的另外三边总长应恰好为24米,要围成的菜园为矩形,如图所示.设边的长为x米,边的长为y米,则y与x之间的函数关系式是(
)
A.
B.
C.
D.
5.如图,直角三角形ABC的两直角边BC、AC分别与x轴、y轴平行,且,顶点A的坐标为,若某正比例函数的图象经过点B,则此正比例函数的表达式为(
)
A.
B.
C.
D.
6.如图,一条直线与两坐标轴的正半轴分别交于两点,P是线段上任意一点(不包括端点),过点P分别作两坐标轴的垂线与两坐标轴围成的矩形的周长为8,则该直线的函数表达式是(
)
A.
B.
C.
D.
7.一个容器有进水管和出水管,每分钟的进水量和出水量是两个常数.从某时刻开始内只进水不出水,从第到第内既进水又出水,从第开始只出水不进水,容器内水量(单位:)与时间(单位:)之间的关系如图所示,则图中的值是(
)
A.32
B.34
C.36
D.38
8.某快递公司每天上午7:00—8:00为集中揽件和派件时段,甲仓库用来揽收快件,乙仓库用来派发快件,该时段内甲、乙两仓库的快件数量y(件)与时间x(分)之间的函数图象如图所示,下列说法正确的有(
)
①15分钟后,甲仓库内快件数量为180件;
②乙仓库每分钟派送快件的数量为4件;
③8:00时,甲仓库内快件数量为400件;
④7:20时,两仓库快件数量相同.
A.1个
B.2个
C.3个
D.4个
9.学校计划购买A和B两种品牌的足球,已知一个A品牌足球60元,一个B品牌足球75元,学校准备将1500元钱全部用于购买这两种足球(两种足球都买),该学校的购买方案共有(
)
A.3种
B.4种
C.5种
D.6种
二.填空题
10.我国很多城市水资源缺乏,为了加强居民的节水意识,某自来水公司采取分段收费方式,某市居民月交水费y(元)与用水量x(吨)之间的关系如图所示,若某户居民4月份用水20吨,则应交水费___________元.
11.已知金属棒的长度l(cm)是温度t(℃)的一次函数.现有一根金属棒,在0℃时的长度是200cm,温度每升高1℃,它就伸长0.002cm,则这根金属棒的长度l(cm)与温度t(℃)的函数关系式为____________.
12.学校与图书馆在同一条笔直道路上,甲从学校去图书馆,乙从图书馆回学校,甲、乙两人都匀速步行且同时出发,乙先到达目的地两人之间的距离y(米)与时间t(分)之间的函数关系如图所示,则乙到达目的地时,甲离目的地还有
米.
三.解答题
13.暑期将至,某健身俱乐部面向学生推出暑期优惠活动,活动方案如下:
方案一:购买一张学生暑期专享卡,每次健身费用按六折优惠;
方案二:不购买学生暑期专享卡,每次健身费用按八折优惠.
设某学生暑期健身x(次),按照方案一所需费用为(元),且;按照方案二所需费用为(元),且.其函数图象如图所示.
(1)求和b的值,并说明它们的实际意义;
(2)求打折前的每次健身费用和的值;
(3)八年级学生小华计划暑期前往该俱乐部健身8次,选择哪种方案所需费用更少?说明理由.
答案以及解析
1.答案:C
解析:由题意可得,故选C.
2.答案:B
解析:依题意得.故选B.
3.答案:A
解析:根据题意可知,甲每分钟比乙快:(米),设乙的速度为x米/分,则甲的速度为米/分,根据题意得,解得,,故甲的速度为60米/分,乙的速度为40米/分,故选A.
4.答案:B
解析:根据题意,得,所以,因为,所以.故选B.
5.答案:A
解析:轴,轴,,顶点A的坐标为,,设正比例函数的表达式为,,解得,正比例函数的表达式为,故选A.
6.答案:A
解析:如图,设过点P的两垂线分别与x轴,y轴的交点为.
设点P的坐标为.
点P在第一象限,.
矩形的周长为8,,.
该直线的函数表达式是.故选A.
7.答案:C
解析:由题图可知每分钟的进水量为,设每分钟的出水量为,则,解得第时,,.
8.答案:C
解析:由题意结合题图可知:
15分钟后,甲仓库内快件数量为130件,故①说法错误;
甲仓库揽收快件的速度为(件/分),
所以8:00时,甲仓库内快件数为(件),故③说法正确;
(分),即45分钟乙仓库派送快件180件,
所以乙仓库每分钟派送快件的数量为(件),故②说法正确;
所以刚开始时乙仓库快件的总数量为(件),
设x分钟后,两仓库快件数量相同,根据题意得,解得,
即7:20时,两仓库快件数量相同,故④说法正确.
所以说法正确的有②③④,共3个.故选C.
9.答案:B
解析:设购买A品牌足球x个,购买B品牌足球y个.根据题意,得.
均为正整数,
或或或
该学校共有4种购买方案.故选B.
10.答案:44
解析:由题图可知,超出10吨的部分,每吨水的价格是(元),当用水20吨时,应交水费:(元),故答案为44.
11.答案:
解析:设l与t的函数关系式为,将代入,可得.由温度每升高1℃,它就伸长0.002cm得,故金属棒的长度l(cm)与温度t(℃)的函数关系式为.
12.答案:800
解析:根据题中的图象信息知,当时,甲、乙两人相遇,甲的速度为米/分,
甲从学校去图书馆,乙从图书馆回学校,甲、乙两人都匀速步行且同时出发,
当时,甲、乙两人相遇,甲、乙两人的速度和为米/分,
乙的速度为米/分乙从图书馆回学校的时间为分钟,
乙到达目的地时,甲离目的地的距离为米.
13.答案:(1)函数图象经过点,,
.解得.
表示的实际意义是购买一张学生暑期专享卡后每次健身费用为15元,
表示的实际意义是购买一张学生暑期专享卡的费用为30元.
(2)由题意可得,折前的每次健身费用为元,
则.
(3)选择方案一所需费用更少.
理由:,.
当健身8次时,选择方案一所需费用为元;
选择方案二所需费用为元,
,选择方案一所需费用更少.
