中考专题复习:《四边形》
图片预览




文档简介
中考专题复习:《四边形》
★★★考点讲解★★★
考点1:平行四边形的性质和判定
一:
平行四边形的定义。两组对边分别平行的四边形是平行四边形,
2.两条平行线间的距离:两条平行线中,一条直线上任意一点到另一条直线的距离,叫做两条平行线间的距离,两条平行线间的距离处处相等.
3.平行四边形的性质:
文字表达:平行四边形的两组对边分别平行;平行四边形的两组对边分别相等;平行四边形的两组对角分别相等;平行四边形的对角线互相平分.
符号语言表达:
四边形ABCD是平行四边形
4.平行四边形的判定:
文字表达:
两组对边分别平行的四边形是平行四边形.
两组对边分别相等的四边形是平行四边形.
一组对边平行且相等的四边形是平行四边形.
两组对角分别相等的四边形是平行四边形.
对角线互相平分的四边形是平行四边形.
图形如图l-4-2:
符号语言表达:
AB∥CD.BC∥AD四边形ABCD是平行四边形
AB=CD,BC=AD四边形ABCD是平行四边形.
AB平行且相等CD或BC平行且相等AD四边形ABCD是平行四边形.
OA=OC,OB=OD四边形ABCD是平行四边形.
∠ABC=∠ADC,∠DAB=∠DCB边形ABCD是平行四边形.
二、经典考题剖析:
1、如图1―4―3,在□ABCD中,如果点M为CD中点,AM与BD相交于点N那么SΔDMN :S□ABCD为( )
A.1:12 B.1:9 C.1:8 D.1:6
2、如图1―4―4,□ABCD中,对角线AC和 BD相交于点O,如果AC=12,BD=10,AB=m,那么m的取值范围是( )
A.1<m<11 B.2<m<22 C.10<m<12 D.5<m<6
3、顺次连接一个任意四边形四边的中点,得到一个 ___________四边形.
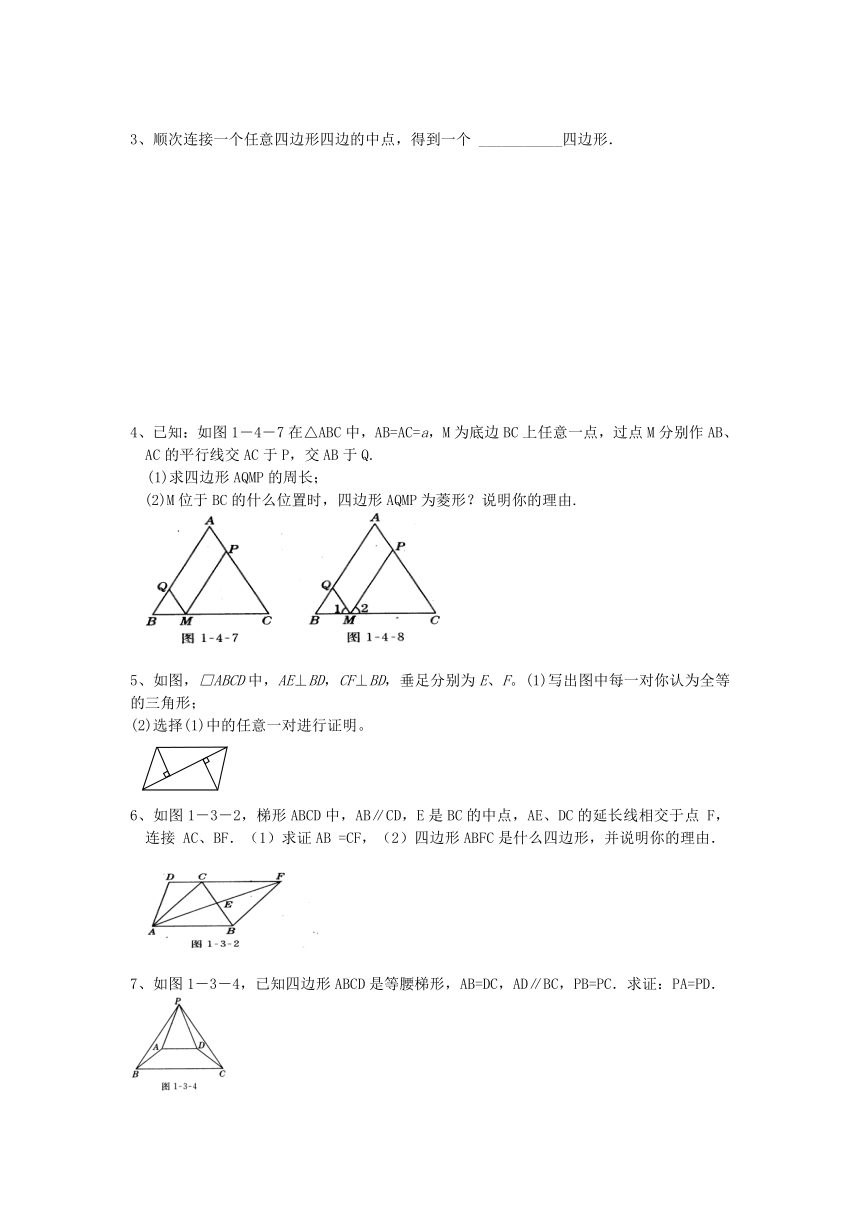
4、已知:如图1―4―7在△ABC中,AB=AC=a,M为底边BC上任意一点,过点M分别作AB、AC的平行线交AC于P,交AB于Q.
(1)求四边形AQMP的周长;
(2)M位于BC的什么位置时,四边形AQMP为菱形?说明你的理由.
5、如图,□ABCD中,AE⊥BD,CF⊥BD,垂足分别为E、F。(1)写出图中每一对你认为全等的三角形;
(2)选择(1)中的任意一对进行证明。
6、如图1-3-2,梯形ABCD中,AB∥CD,E是BC的中点,AE、DC的延长线相交于点 F,连接 AC、BF.(1)求证AB =CF,(2)四边形ABFC是什么四边形,并说明你的理由.
7、如图1-3-4,已知四边形ABCD是等腰梯形,AB=DC,AD∥BC,PB=PC.求证:PA=PD.
8、.平行四边形一组对角的平分线( )
A.在同一条直线上. B.平行 C.相交 D.平行或在同一直线上
在平行四边形ABCD中,AB=3,BC=4,∠ABC的平分线交AD于E,∠BCD的平分线交AD于F,BE和CF相交于点G,FG=1,(1)求证:AF=DE;(2)求∠A的度数。
9、如图,在平面直角坐标系中,□OABC的顶点A在轴上,顶点B
的坐标为(6,4).若直线l经过点(1,0),且将□OABC分割成
面积相等的两部分,则直线l的函数解析式是( )
A. B. C. D.
10、如图,在□ABCD中,AB=3,AD=4,∠ABC=60°,过BC的中点E作EF⊥AB,垂足为点F,与DC的延长线相交于点H,则△DEF的面积是 .
11、如图,在ABCD中,已知AB=9㎝,AD=6㎝,BE平分∠ABC交DC边于点E,则DE等
于 ㎝.
三、针对性训练:
1.在□ABCD中,∠C=∠B+∠D,则∠A=____
2.已知□ABCD的周长为30㎝,AB:BC=2:3,那么CD=___________㎝.
3.平行四边形的面积为144㎝2 ,若相邻两边上的高分别为8cm和12cm,则这两个邻边的长分别是 _______和______,平行四边形的周长是_______.
4.在四边形ABCD中,给出下列条件:
①AB∥CD,②AD=BC,③∠A=∠C,④AD∥BC.能判断四边形是平行四边形的组合是_______.
5.下面给出四边形ABCD中∠A、∠B、∠C、∠D的度数之比,其中能判别四边形ABCD是平行四边形的是()
A.l:2:3:4 B.2:3:2:3 C.2:3:3:2 D.1:2:2:3
6、以不在同一直线上的三点作平行四边形的三个顶点,则可作出平行四边形( )
A.1个 B.2个 C.3个 D.4个
7.如图1―4―10,在□ABCD中,CE是 ∠DCB的平分线,F是 AB的中点,AB=6,BC=4,EF为多少?
8.如图1―4―11,已知等边三角形ABC的边长为a, P是△ABC内一点,PD∥AB,PE∥BC,PF ∥AC,点D、E、F分别在 BC、AC、AB上,猜想:PD+PE+PF=______,并证明你的猜想.
9.如图1―4―12,在平行四边形ABCD中,点E、F 在对角线AC上,且AE=CF,请你以F为一个端点,和图中已标明字母的某一个点连成一条新线段,猜想并证明它和图中已有的某一条线段相等.(只需说明一组线段相等即可)
(1)连接_______;(2)猜想________
(3)说明理由.
10、如图1―4―13,某村有一块四边形池塘,在它的四个角A、B、C、D处均有一棵大核桃树,此村准备开挖池塘建养鱼池,想使池塘的面积扩大一倍,又保持核桃树不动,并要求扩建后的池塘成平行四边形状,你认为该村能否实现这一设想?若能,请你设计并画出图形;若不能请说明理由.
11、如图,在平行四边形ABCD中(AB≠BC),直线EF经过其对角线的交点O,且分别交AD、BC于点M、N,交BA、DC的延长线于点E、F,下列结论:①AO=BO;②OE=OF;③△EAM∽△EBN;④△EAO≌△CNO,其中正确的是( )
A、①② B、②③ C、②④ D、③④
考点2:矩形、菱形、正方形的性质 和判定
一、考点讲解:
l.菱形的性质:①菱形的四条边都相等.
②菱形的对角线互相垂直,并且每条对角线平分一组对角.
③具有平行四边形所有性质.
菱形的判定:①对角线互相垂直的平行四边形是菱形.
②一组邻边相等的平行四边形是菱形.
③四条边都相等的四边形是菱形.
3.矩形的性质:①矩形的四个角都是直角.
②矩形的对角线相等.
③矩形具有平行四边形的所有性质.
4.矩形的判定:①有一个角是直角的平行四边形是矩形.
②对角线相等的平行四边形是矩形.
③有三个角是直角的四边形是矩形.
5.正方形的性质:①正方形的四个角都是直角,四条边都相等.
②正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角.
6.正方形的判定:①有一个角是直角的柳是正方形.
②有一组邻边相等的矩形是正方形.
③对角线相等的菱形是正方形.
④对角线互相垂直的矩形是正方形.
二、经典考题剖析:
1、如图1―4―15,矩形ABCD中 ,E在 AD上,且EF⊥EC,EF=EC,DE=2,矩形的周长为16,则AE的长是( )
A.3 B.4 C.5 D.7
2、如图1―4―16,菱形A B CD的对角线的长分别为2和5,P是对角线AC上任一点(点P不与点A、C重合)且PE∥BC交AB于 E,PF∥CD交AD于F,则阴影部分的面积是___
3、如图,矩形ABCD中,AB=3,BC=4,如果将该矩形沿对角线BD折叠,那么图中阴影部分的面积是_________
4、如图l-3-12,菱形ABCD的一条对角线BD上一点O到菱形一边AB的距离为2,那么点O到另一边BC的距离为_________.
5.在梯形ABCD中,AB∥CD,E、F、G、H分别是AB、BC、CD、DA边上的中点,当梯形ABCD满足___________条件时,四边形EWIH是菱形.
6.如图l-3-13,边长为3的正方形ABCD,绕点C按顺时针方向旋转30°后得到正方形EFCG,EF交AD于点H,那么DH的长为_______.
7.如图l-3-14,矩形纸片ABCD中,AB=6,E为AD边上一点,将纸片沿BE折叠后,点A落在CD边上的F点,若∠CBF=∠EBF,则BC边的长为( )
A. B.2 C.3 D.+1
8.已知:如图1-3-l5,在矩形ABCD中,点E、F在BC边上,且BE=CF,AF、DE交于点M,求证:AM=DM。
9.延长等腰三角形ABC顶角平分线AD到E,使DE=AD,连结BE、CE,则四边形ABEC是_____形.
10.菱形的周长为40cm,它的一条对角线长为10cm,则菱形相邻的两个角分别是_______和_________.
11.正方形的对角线长为a,则它的对角线的交点到各边的距离为( )
A、a B、a C、 D、2a
12、 如图1―4―2l,在边长为a的菱形ABCD中,∠DAB=60°,E是异于A、D两点的动点,F是CD上的动点,满足A E+CF=a,说明:不论E、F怎样移动,三角形BEF总是正三角形.
13、 已知如图l-4-22,E是矩形ABCD边AD上一点,且BE=ED,P是对角线BD上任一点,PF⊥BE,PG⊥AD,垂足分别为F、G,则PF+PG=AB成立吗?为什么?
14、在一次数学兴趣小组活动中,组长将两条等宽的长纸条倾斜地重叠着,并问同学,重叠部分是一个什么样的四边形?同学说:这是一个平行四边形.乙同学说:这是一个菱形.
请问:你同意谁的看法.要解决此题,需建构数学模型,将实际问题转化成数学问题来解决,即已知:如图1-4-24,四边形ABCD中,AB∥CD,AD∥BC,边CD与边BC上的高相等,试判断四边形 ABCD的形状.
15 如图1-4-25,在△ABC中,∠ACB=90○ ,BC的垂直平分线DE交BC于D,交AB于E,F在DE的延长线上,并且AF=CE.
(1)求证:四边形ACEF是平行四边形;
(2)当上B的大小满足什么条件时,四边形A CEF是菱形?请回答并证明你的结论;
(3)四边形A CEF有可能为正方形吗?为什么?
.
16、如图1-3-18,已知正方形 ABCD的对角线AC、BD相交于点O,E是AC上一点,连结EB.过A作AM⊥BE,垂足为M,AM交BD于点F.(1)求证:OE=OF;
(2)如图1-3-19,若点E在 AC的延长线上,AM⊥BE于点M,交DB的延长线于点F,其他条件不变,则结论“OE=OF”还成立吗?如果成立.请给出证明:如果不成立,请说明理由.
17、如图 1-3-20,四边形ABCD是平行四边形,对角线 AC、BD交于点O,过点 O画直线EF,分别交AD、BC于点E、F.求证:OE=OF.
18、如图1-3-21,点P是边长为1的菱形ABCD对角线AC上一个动点,点M、N分别是AB、BC边上的中点,MP + NP的最小值是( )
A.2 B、1 C、 D、
19、如图1-3-24,顺次连结四边形ABCD各边中点得四边形EFGH,要使四边形EFGH为矩形,应添加的条件是( )
A.A B∥CD B.A C=BD C.AC⊥BD D、AB=DC
20、如图l-3-32,已知在等腰梯形ABCD中,AD∥BC.
⑴若AD=5,BC=11,梯形的高是4,求梯形的周长;
⑵若AD=3,BC=7,BD=5,求证AC⊥BD.
21、(探究题)如图 l-3-33①已知:矩形ABCD
中,AD>AB,O为对角线的交点,过D点作一直线分别交BC、AD于 M、N.
(1)求证:梯形ABMN的面积等于梯形CDNM的面积;
(2)当MN满足什么条件时,将矩形ABCD沿折痕翻折后就使点C恰好与A点重合,如图l-3-33②(只写出满足条件,不要求证明)
22、(探究题)如图l-3-35,矩形ABCD中,
O是AC与BD的交点,过O点的直线EF与AB、CD的延长线分别交于E、F.(l)求证:△BOE≌△DOF;(2)当EF与AC满足什么条件时,四边形AECF是菱形,并证明你的结论.
考点3:等腰梯形的性质和判定
一、考点讲解:
1.定义:一组对边平行,另一组对进不平行的四边形叫梯形.两腰相等的梯形叫等腰梯形.一腰和底垂直的梯形叫做直角梯形.
2、等腰梯形的性质:等腰梯形同一底上的两个角相等;等腰梯形的对角线相等.
3.等腰梯形的判定:①同一底上的两个角相等的梯形是等腰梯形.②对角线相等的梯形是等腰梯形.
4.等腰梯形常见的作辅助线的方法.
(1)作等腰梯形的两条高,将等腰梯形分成一个矩形和两个全等直角三角形,如图l-4-26
(2)平移一腰,将等腰梯形化成一个平行四边形和一个等腰三角形.如图l-4-27.
(3)平移对角线,将等腰梯形转化为等腰三角形,如图l-4-28.
(4)如果题中有一腰的中点,则可连结上底的一个顶点和一腰的中点并延长交下底一点,如图1-4-29.
二、经典考题剖析:
1、已知:在等腰梯形 ABCD中,AD∥BC,对角线AC⊥BD,AD=3cm,BC=7cm,则梯形的高是_________cm.
2、某生活小区的居民筹集资金1600元,计划在一块上、下底分别为10,20的梯形空地上种植花木(如图10-1)
⑴他们在△AMD和△BMC地带上种植太阳花,单价为8元/,当△AMD地带种满花后(图10-1中阴影部分),共花了160元,请计算种满△BMC地带所需的费用。
⑵若其余地带要种的有玫瑰和茉莉花两种花木可供选择,单价分别为12元/和10元/,应选择哪种花木,刚好用完所筹集的资金?
⑶若梯形ABCD为等腰梯形,面积不变(如图10-2),请你设计一种花坛图案,即在梯形内找到一点P,使得△APB≌△DPC且S△APD=S△BPC,并说出你的理由。
3.等腰梯形上底与高相等,下底是高的3倍,则底角为( )
A.30o B.45 o C.60 o D.75 o
4.若等腰梯形两底之差等于一腰的长,则腰与下底的夹角为( )
A.60 o B.30 o C.45 o D.15 o
5.如图l-4-35,在梯形ABCD中,AD∥BC,AB=AD+BC,E是CD的中点,说明:
(1)AE与BE有怎样的位置关系?为什么?
(2)AE、BE是否是∠BAD和∠ABC的平分线?请说明理由.
6、如图1-4-37,在梯形ABCD中,AD∥BC,∠B= 90○ ,AD=24cm,AB=8cm,BC=26cm,动点P从A点开始沿边AD向D以1cm/秒的速度运动,动点Q从C点开始沿CB边向B以3cm/秒的速度运动,P、Q分别从A、C同时出发,当其中一点到达端点时,另一点也随之停止运动,设运动时间为t秒,t分别为何值时,四边形PQCD是平行四边形、等腰梯形?
7、 如图1-4-38,等腰梯形ABCD中,AD∥BC,AB =CD,∠ DBC=45○ ,翻折梯形使点B重合于点 D,折痕分别交边 AB、BC于点F、E,若AD=2,BC=8,求BE的长.
考点4:多边形的内角和及外角和
一、考点讲解:
1.多边形的定义:在平面内,由若干条不在同一条直线上的线段;首尾顺次相接组成的封闭图形叫做多边形,在多边形中,组成多边形的各条线段叫做多边形的边,每相邻两条边的公共点叫做多边形的顶点,连接不相邻两个顶点的线段叫做多边形的对角线.
2.多边形的内角和:n边形的内角和=(n-2)180°.
3.正多边形:在平面内,内角都相等,边也相等的多边形叫做正多边形.
4.多边形的外角:多边形内角的一边与另一边的反向延长线所组成的角,叫做这个多边形的外角.在多边形的每个顶点处取这个多边形的一个外角,它们 的和叫做多边形的外角和,多边形的外角和都等于360°.
5.过n边形的一个顶点共有(n-3)条对角线,n边形共有条对角线.
6.过n边形的一个顶点将n边形分成(n-2)个三角形.
二、经典考题剖析:
1、正n边形的内角和等于1080°,那么这个正n边形的边数n=______
2.n边形的每个内角等都等于120○ ,则n等于_____
3.一个正多边形的每个外角都是36○ ,则这个多边形是_________边形.
4.一个多边形的外角和等于它内角和的,则这个多边形的边数为____________-.
考点5:平面的密铺
一、考点讲解:
1.定义:把形状、大小完全相同的一种或几种平面图形拼接在一起,使得平面上不留空隙,不重叠,这就是平面图形的密铺,也叫平面图形的镶嵌.
2.对于限于用一种图形密铺的问题,有三角形、四边形和正六边形,如果能实现平面图形的密铺,密铺图的每个顶点都必须集中在几个多边形的顶角,于是在每个顶点集中的顶角刚好拼成一个周角.
二、经典考题剖析:
1、如果要用正三角形和正方形两种图形进行密铺,那么至少需要( )
A.三个正三角形,两个正方形
B.两个正三角形,三个正方形
C.两。河三角形,两个正方形
D.三个正三角形,三个正方形
2、使用同一种规格的下列地砖,不能密铺的是( )
A.正六边形地砖 B正五边形地砖 C.正方形地砖 D正三角形地砖
3.用正四边形一种图形进行平面图形的密铺时,在它的一个顶点周围的正四边形的个数为_______.
考点6:中心对称图形
一、考点讲解:
1.定义:在平面内,一个图形绕某个点旋转180○ ,如果旋转前后的图形互相重合,那么这个图形叫做中心对称图形,这个点叫做它的对称中心.
2.性质:中心对称图形上的每一对对应点所连成的线段都被对称中心平分.
3.中心对称与旋转对称的关系:中心对称是旋转角是180o的旋转对称.
4.中心对称的判定:如果两个点的连线被某一点M平分,则这两个点关于点M成中心对称.
二、经典考题剖析:
1、是国际运用的交通标志,其中不是中心对称图形的是( )
2、在我们学过的图形:线段、直线、射线、角、等腰三角形、平行四边形、矩形展形、正方形、等腰梯形、圆中,其中轴对称图形是一,中心对称图形是_______________,既是轴对称图形又是中心对称图形的是_______________.
★★★新课标中考题★★★
1、如图1-4-53,矩形ABCD中,AC与 BD交于 O点,BE⊥AC于 E,CF⊥BD于 F.求证:BE=CF.
2、如图l-4-54,梯形ABCD中,AB∥DC,∠B=90°,E为BC上一点,且AE⊥ED.若 BC=12,DC=7,BE:EC=1:2,求AB的长
3、如图1-4-56,将矩形ABCD沿对角线BD折叠,使C落在C'处,BC'交AD于E,则下列结论不一定成立的是( )
A、AD=BC′
B、∠EBD=∠EDB
C、△ABE∽△CBD
D、
4、已知:如图1-4-56,AG∥BC,DE∥AG,GF∥AB,点E为AC的中点,求证:DE=FC
5、如图1-4-58,Rt△ABC中,A=90,AB=4,AC=3,D在BC上运动(不与B、C重合),过D点分别向AB、Ac作垂线,垂足分别为E、F,则矩形AEDF的面积的最大值
________________
6、在直线l上依次摆放着七个正方形(如图1-4-60所示)。已知斜放置的三个正方形的面积分别是1、2、3,正放置的四个正方形的面积依次是S1、S2、S3、S4,则S1+S2+S3+S4=_________。
7、如图1-4-63,矩形ABCD中,AB=8,BC=6,对角线AC上有一个动点P(不包括点A和点C).设AP=x,四边形PBCD的面积为y.
(1)写出y与x的函数关系,并确定自变量x范围.
(2)有人提出一个判断:“关于动点P,⊿PBC面积与ΔPAD面积之和为常数”.请你说明此判断是否正确,并说明理由
8、从等腰三角形底边上任意一点分别作两腰的平行线,与两腰所围成的平行四边形的周长等于三角形的( )
A.两腰长的和 B.周长的一半 C.周长 D.一腰长与底边长的和
9、如图1-4-68,在菱形ABCD中,∠BAD=80 ,AB的垂直平分线EF交对角线A C于点F、E为垂足,连结DF,则∠CDF等于( )
A.80° B.70° C.65° D.60°
10、直角梯形下底与一腰的夹角为60°,此腰与上底长都为8,则中位线长为_______.
11、(探究题)如图如图1-4-79,在矩形AB CD中,AB=12cm,BC=6cm,点P沿AB边从点A开始向点B以2cm/秒的速度移动;点Q沿DA边从点D开始向点A以1cm/秒的速度移动,如果P对同时出发,用t(秒)表示移动的时间(0<t<6),那么:
(1)当t为何值时,△QAP为等腰直角三角形?
(2)求四边形QAPC的面积,提出一个与计算结果有关的结论
A
B
C
D
E
F
x
y
O
A
B
C
第9题
C
D
E
H
A
B
F
第10题
★★★考点讲解★★★
考点1:平行四边形的性质和判定
一:
平行四边形的定义。两组对边分别平行的四边形是平行四边形,
2.两条平行线间的距离:两条平行线中,一条直线上任意一点到另一条直线的距离,叫做两条平行线间的距离,两条平行线间的距离处处相等.
3.平行四边形的性质:
文字表达:平行四边形的两组对边分别平行;平行四边形的两组对边分别相等;平行四边形的两组对角分别相等;平行四边形的对角线互相平分.
符号语言表达:
四边形ABCD是平行四边形
4.平行四边形的判定:
文字表达:
两组对边分别平行的四边形是平行四边形.
两组对边分别相等的四边形是平行四边形.
一组对边平行且相等的四边形是平行四边形.
两组对角分别相等的四边形是平行四边形.
对角线互相平分的四边形是平行四边形.
图形如图l-4-2:
符号语言表达:
AB∥CD.BC∥AD四边形ABCD是平行四边形
AB=CD,BC=AD四边形ABCD是平行四边形.
AB平行且相等CD或BC平行且相等AD四边形ABCD是平行四边形.
OA=OC,OB=OD四边形ABCD是平行四边形.
∠ABC=∠ADC,∠DAB=∠DCB边形ABCD是平行四边形.
二、经典考题剖析:
1、如图1―4―3,在□ABCD中,如果点M为CD中点,AM与BD相交于点N那么SΔDMN :S□ABCD为( )
A.1:12 B.1:9 C.1:8 D.1:6
2、如图1―4―4,□ABCD中,对角线AC和 BD相交于点O,如果AC=12,BD=10,AB=m,那么m的取值范围是( )
A.1<m<11 B.2<m<22 C.10<m<12 D.5<m<6
3、顺次连接一个任意四边形四边的中点,得到一个 ___________四边形.
4、已知:如图1―4―7在△ABC中,AB=AC=a,M为底边BC上任意一点,过点M分别作AB、AC的平行线交AC于P,交AB于Q.
(1)求四边形AQMP的周长;
(2)M位于BC的什么位置时,四边形AQMP为菱形?说明你的理由.
5、如图,□ABCD中,AE⊥BD,CF⊥BD,垂足分别为E、F。(1)写出图中每一对你认为全等的三角形;
(2)选择(1)中的任意一对进行证明。
6、如图1-3-2,梯形ABCD中,AB∥CD,E是BC的中点,AE、DC的延长线相交于点 F,连接 AC、BF.(1)求证AB =CF,(2)四边形ABFC是什么四边形,并说明你的理由.
7、如图1-3-4,已知四边形ABCD是等腰梯形,AB=DC,AD∥BC,PB=PC.求证:PA=PD.
8、.平行四边形一组对角的平分线( )
A.在同一条直线上. B.平行 C.相交 D.平行或在同一直线上
在平行四边形ABCD中,AB=3,BC=4,∠ABC的平分线交AD于E,∠BCD的平分线交AD于F,BE和CF相交于点G,FG=1,(1)求证:AF=DE;(2)求∠A的度数。
9、如图,在平面直角坐标系中,□OABC的顶点A在轴上,顶点B
的坐标为(6,4).若直线l经过点(1,0),且将□OABC分割成
面积相等的两部分,则直线l的函数解析式是( )
A. B. C. D.
10、如图,在□ABCD中,AB=3,AD=4,∠ABC=60°,过BC的中点E作EF⊥AB,垂足为点F,与DC的延长线相交于点H,则△DEF的面积是 .
11、如图,在ABCD中,已知AB=9㎝,AD=6㎝,BE平分∠ABC交DC边于点E,则DE等
于 ㎝.
三、针对性训练:
1.在□ABCD中,∠C=∠B+∠D,则∠A=____
2.已知□ABCD的周长为30㎝,AB:BC=2:3,那么CD=___________㎝.
3.平行四边形的面积为144㎝2 ,若相邻两边上的高分别为8cm和12cm,则这两个邻边的长分别是 _______和______,平行四边形的周长是_______.
4.在四边形ABCD中,给出下列条件:
①AB∥CD,②AD=BC,③∠A=∠C,④AD∥BC.能判断四边形是平行四边形的组合是_______.
5.下面给出四边形ABCD中∠A、∠B、∠C、∠D的度数之比,其中能判别四边形ABCD是平行四边形的是()
A.l:2:3:4 B.2:3:2:3 C.2:3:3:2 D.1:2:2:3
6、以不在同一直线上的三点作平行四边形的三个顶点,则可作出平行四边形( )
A.1个 B.2个 C.3个 D.4个
7.如图1―4―10,在□ABCD中,CE是 ∠DCB的平分线,F是 AB的中点,AB=6,BC=4,EF为多少?
8.如图1―4―11,已知等边三角形ABC的边长为a, P是△ABC内一点,PD∥AB,PE∥BC,PF ∥AC,点D、E、F分别在 BC、AC、AB上,猜想:PD+PE+PF=______,并证明你的猜想.
9.如图1―4―12,在平行四边形ABCD中,点E、F 在对角线AC上,且AE=CF,请你以F为一个端点,和图中已标明字母的某一个点连成一条新线段,猜想并证明它和图中已有的某一条线段相等.(只需说明一组线段相等即可)
(1)连接_______;(2)猜想________
(3)说明理由.
10、如图1―4―13,某村有一块四边形池塘,在它的四个角A、B、C、D处均有一棵大核桃树,此村准备开挖池塘建养鱼池,想使池塘的面积扩大一倍,又保持核桃树不动,并要求扩建后的池塘成平行四边形状,你认为该村能否实现这一设想?若能,请你设计并画出图形;若不能请说明理由.
11、如图,在平行四边形ABCD中(AB≠BC),直线EF经过其对角线的交点O,且分别交AD、BC于点M、N,交BA、DC的延长线于点E、F,下列结论:①AO=BO;②OE=OF;③△EAM∽△EBN;④△EAO≌△CNO,其中正确的是( )
A、①② B、②③ C、②④ D、③④
考点2:矩形、菱形、正方形的性质 和判定
一、考点讲解:
l.菱形的性质:①菱形的四条边都相等.
②菱形的对角线互相垂直,并且每条对角线平分一组对角.
③具有平行四边形所有性质.
菱形的判定:①对角线互相垂直的平行四边形是菱形.
②一组邻边相等的平行四边形是菱形.
③四条边都相等的四边形是菱形.
3.矩形的性质:①矩形的四个角都是直角.
②矩形的对角线相等.
③矩形具有平行四边形的所有性质.
4.矩形的判定:①有一个角是直角的平行四边形是矩形.
②对角线相等的平行四边形是矩形.
③有三个角是直角的四边形是矩形.
5.正方形的性质:①正方形的四个角都是直角,四条边都相等.
②正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角.
6.正方形的判定:①有一个角是直角的柳是正方形.
②有一组邻边相等的矩形是正方形.
③对角线相等的菱形是正方形.
④对角线互相垂直的矩形是正方形.
二、经典考题剖析:
1、如图1―4―15,矩形ABCD中 ,E在 AD上,且EF⊥EC,EF=EC,DE=2,矩形的周长为16,则AE的长是( )
A.3 B.4 C.5 D.7
2、如图1―4―16,菱形A B CD的对角线的长分别为2和5,P是对角线AC上任一点(点P不与点A、C重合)且PE∥BC交AB于 E,PF∥CD交AD于F,则阴影部分的面积是___
3、如图,矩形ABCD中,AB=3,BC=4,如果将该矩形沿对角线BD折叠,那么图中阴影部分的面积是_________
4、如图l-3-12,菱形ABCD的一条对角线BD上一点O到菱形一边AB的距离为2,那么点O到另一边BC的距离为_________.
5.在梯形ABCD中,AB∥CD,E、F、G、H分别是AB、BC、CD、DA边上的中点,当梯形ABCD满足___________条件时,四边形EWIH是菱形.
6.如图l-3-13,边长为3的正方形ABCD,绕点C按顺时针方向旋转30°后得到正方形EFCG,EF交AD于点H,那么DH的长为_______.
7.如图l-3-14,矩形纸片ABCD中,AB=6,E为AD边上一点,将纸片沿BE折叠后,点A落在CD边上的F点,若∠CBF=∠EBF,则BC边的长为( )
A. B.2 C.3 D.+1
8.已知:如图1-3-l5,在矩形ABCD中,点E、F在BC边上,且BE=CF,AF、DE交于点M,求证:AM=DM。
9.延长等腰三角形ABC顶角平分线AD到E,使DE=AD,连结BE、CE,则四边形ABEC是_____形.
10.菱形的周长为40cm,它的一条对角线长为10cm,则菱形相邻的两个角分别是_______和_________.
11.正方形的对角线长为a,则它的对角线的交点到各边的距离为( )
A、a B、a C、 D、2a
12、 如图1―4―2l,在边长为a的菱形ABCD中,∠DAB=60°,E是异于A、D两点的动点,F是CD上的动点,满足A E+CF=a,说明:不论E、F怎样移动,三角形BEF总是正三角形.
13、 已知如图l-4-22,E是矩形ABCD边AD上一点,且BE=ED,P是对角线BD上任一点,PF⊥BE,PG⊥AD,垂足分别为F、G,则PF+PG=AB成立吗?为什么?
14、在一次数学兴趣小组活动中,组长将两条等宽的长纸条倾斜地重叠着,并问同学,重叠部分是一个什么样的四边形?同学说:这是一个平行四边形.乙同学说:这是一个菱形.
请问:你同意谁的看法.要解决此题,需建构数学模型,将实际问题转化成数学问题来解决,即已知:如图1-4-24,四边形ABCD中,AB∥CD,AD∥BC,边CD与边BC上的高相等,试判断四边形 ABCD的形状.
15 如图1-4-25,在△ABC中,∠ACB=90○ ,BC的垂直平分线DE交BC于D,交AB于E,F在DE的延长线上,并且AF=CE.
(1)求证:四边形ACEF是平行四边形;
(2)当上B的大小满足什么条件时,四边形A CEF是菱形?请回答并证明你的结论;
(3)四边形A CEF有可能为正方形吗?为什么?
.
16、如图1-3-18,已知正方形 ABCD的对角线AC、BD相交于点O,E是AC上一点,连结EB.过A作AM⊥BE,垂足为M,AM交BD于点F.(1)求证:OE=OF;
(2)如图1-3-19,若点E在 AC的延长线上,AM⊥BE于点M,交DB的延长线于点F,其他条件不变,则结论“OE=OF”还成立吗?如果成立.请给出证明:如果不成立,请说明理由.
17、如图 1-3-20,四边形ABCD是平行四边形,对角线 AC、BD交于点O,过点 O画直线EF,分别交AD、BC于点E、F.求证:OE=OF.
18、如图1-3-21,点P是边长为1的菱形ABCD对角线AC上一个动点,点M、N分别是AB、BC边上的中点,MP + NP的最小值是( )
A.2 B、1 C、 D、
19、如图1-3-24,顺次连结四边形ABCD各边中点得四边形EFGH,要使四边形EFGH为矩形,应添加的条件是( )
A.A B∥CD B.A C=BD C.AC⊥BD D、AB=DC
20、如图l-3-32,已知在等腰梯形ABCD中,AD∥BC.
⑴若AD=5,BC=11,梯形的高是4,求梯形的周长;
⑵若AD=3,BC=7,BD=5,求证AC⊥BD.
21、(探究题)如图 l-3-33①已知:矩形ABCD
中,AD>AB,O为对角线的交点,过D点作一直线分别交BC、AD于 M、N.
(1)求证:梯形ABMN的面积等于梯形CDNM的面积;
(2)当MN满足什么条件时,将矩形ABCD沿折痕翻折后就使点C恰好与A点重合,如图l-3-33②(只写出满足条件,不要求证明)
22、(探究题)如图l-3-35,矩形ABCD中,
O是AC与BD的交点,过O点的直线EF与AB、CD的延长线分别交于E、F.(l)求证:△BOE≌△DOF;(2)当EF与AC满足什么条件时,四边形AECF是菱形,并证明你的结论.
考点3:等腰梯形的性质和判定
一、考点讲解:
1.定义:一组对边平行,另一组对进不平行的四边形叫梯形.两腰相等的梯形叫等腰梯形.一腰和底垂直的梯形叫做直角梯形.
2、等腰梯形的性质:等腰梯形同一底上的两个角相等;等腰梯形的对角线相等.
3.等腰梯形的判定:①同一底上的两个角相等的梯形是等腰梯形.②对角线相等的梯形是等腰梯形.
4.等腰梯形常见的作辅助线的方法.
(1)作等腰梯形的两条高,将等腰梯形分成一个矩形和两个全等直角三角形,如图l-4-26
(2)平移一腰,将等腰梯形化成一个平行四边形和一个等腰三角形.如图l-4-27.
(3)平移对角线,将等腰梯形转化为等腰三角形,如图l-4-28.
(4)如果题中有一腰的中点,则可连结上底的一个顶点和一腰的中点并延长交下底一点,如图1-4-29.
二、经典考题剖析:
1、已知:在等腰梯形 ABCD中,AD∥BC,对角线AC⊥BD,AD=3cm,BC=7cm,则梯形的高是_________cm.
2、某生活小区的居民筹集资金1600元,计划在一块上、下底分别为10,20的梯形空地上种植花木(如图10-1)
⑴他们在△AMD和△BMC地带上种植太阳花,单价为8元/,当△AMD地带种满花后(图10-1中阴影部分),共花了160元,请计算种满△BMC地带所需的费用。
⑵若其余地带要种的有玫瑰和茉莉花两种花木可供选择,单价分别为12元/和10元/,应选择哪种花木,刚好用完所筹集的资金?
⑶若梯形ABCD为等腰梯形,面积不变(如图10-2),请你设计一种花坛图案,即在梯形内找到一点P,使得△APB≌△DPC且S△APD=S△BPC,并说出你的理由。
3.等腰梯形上底与高相等,下底是高的3倍,则底角为( )
A.30o B.45 o C.60 o D.75 o
4.若等腰梯形两底之差等于一腰的长,则腰与下底的夹角为( )
A.60 o B.30 o C.45 o D.15 o
5.如图l-4-35,在梯形ABCD中,AD∥BC,AB=AD+BC,E是CD的中点,说明:
(1)AE与BE有怎样的位置关系?为什么?
(2)AE、BE是否是∠BAD和∠ABC的平分线?请说明理由.
6、如图1-4-37,在梯形ABCD中,AD∥BC,∠B= 90○ ,AD=24cm,AB=8cm,BC=26cm,动点P从A点开始沿边AD向D以1cm/秒的速度运动,动点Q从C点开始沿CB边向B以3cm/秒的速度运动,P、Q分别从A、C同时出发,当其中一点到达端点时,另一点也随之停止运动,设运动时间为t秒,t分别为何值时,四边形PQCD是平行四边形、等腰梯形?
7、 如图1-4-38,等腰梯形ABCD中,AD∥BC,AB =CD,∠ DBC=45○ ,翻折梯形使点B重合于点 D,折痕分别交边 AB、BC于点F、E,若AD=2,BC=8,求BE的长.
考点4:多边形的内角和及外角和
一、考点讲解:
1.多边形的定义:在平面内,由若干条不在同一条直线上的线段;首尾顺次相接组成的封闭图形叫做多边形,在多边形中,组成多边形的各条线段叫做多边形的边,每相邻两条边的公共点叫做多边形的顶点,连接不相邻两个顶点的线段叫做多边形的对角线.
2.多边形的内角和:n边形的内角和=(n-2)180°.
3.正多边形:在平面内,内角都相等,边也相等的多边形叫做正多边形.
4.多边形的外角:多边形内角的一边与另一边的反向延长线所组成的角,叫做这个多边形的外角.在多边形的每个顶点处取这个多边形的一个外角,它们 的和叫做多边形的外角和,多边形的外角和都等于360°.
5.过n边形的一个顶点共有(n-3)条对角线,n边形共有条对角线.
6.过n边形的一个顶点将n边形分成(n-2)个三角形.
二、经典考题剖析:
1、正n边形的内角和等于1080°,那么这个正n边形的边数n=______
2.n边形的每个内角等都等于120○ ,则n等于_____
3.一个正多边形的每个外角都是36○ ,则这个多边形是_________边形.
4.一个多边形的外角和等于它内角和的,则这个多边形的边数为____________-.
考点5:平面的密铺
一、考点讲解:
1.定义:把形状、大小完全相同的一种或几种平面图形拼接在一起,使得平面上不留空隙,不重叠,这就是平面图形的密铺,也叫平面图形的镶嵌.
2.对于限于用一种图形密铺的问题,有三角形、四边形和正六边形,如果能实现平面图形的密铺,密铺图的每个顶点都必须集中在几个多边形的顶角,于是在每个顶点集中的顶角刚好拼成一个周角.
二、经典考题剖析:
1、如果要用正三角形和正方形两种图形进行密铺,那么至少需要( )
A.三个正三角形,两个正方形
B.两个正三角形,三个正方形
C.两。河三角形,两个正方形
D.三个正三角形,三个正方形
2、使用同一种规格的下列地砖,不能密铺的是( )
A.正六边形地砖 B正五边形地砖 C.正方形地砖 D正三角形地砖
3.用正四边形一种图形进行平面图形的密铺时,在它的一个顶点周围的正四边形的个数为_______.
考点6:中心对称图形
一、考点讲解:
1.定义:在平面内,一个图形绕某个点旋转180○ ,如果旋转前后的图形互相重合,那么这个图形叫做中心对称图形,这个点叫做它的对称中心.
2.性质:中心对称图形上的每一对对应点所连成的线段都被对称中心平分.
3.中心对称与旋转对称的关系:中心对称是旋转角是180o的旋转对称.
4.中心对称的判定:如果两个点的连线被某一点M平分,则这两个点关于点M成中心对称.
二、经典考题剖析:
1、是国际运用的交通标志,其中不是中心对称图形的是( )
2、在我们学过的图形:线段、直线、射线、角、等腰三角形、平行四边形、矩形展形、正方形、等腰梯形、圆中,其中轴对称图形是一,中心对称图形是_______________,既是轴对称图形又是中心对称图形的是_______________.
★★★新课标中考题★★★
1、如图1-4-53,矩形ABCD中,AC与 BD交于 O点,BE⊥AC于 E,CF⊥BD于 F.求证:BE=CF.
2、如图l-4-54,梯形ABCD中,AB∥DC,∠B=90°,E为BC上一点,且AE⊥ED.若 BC=12,DC=7,BE:EC=1:2,求AB的长
3、如图1-4-56,将矩形ABCD沿对角线BD折叠,使C落在C'处,BC'交AD于E,则下列结论不一定成立的是( )
A、AD=BC′
B、∠EBD=∠EDB
C、△ABE∽△CBD
D、
4、已知:如图1-4-56,AG∥BC,DE∥AG,GF∥AB,点E为AC的中点,求证:DE=FC
5、如图1-4-58,Rt△ABC中,A=90,AB=4,AC=3,D在BC上运动(不与B、C重合),过D点分别向AB、Ac作垂线,垂足分别为E、F,则矩形AEDF的面积的最大值
________________
6、在直线l上依次摆放着七个正方形(如图1-4-60所示)。已知斜放置的三个正方形的面积分别是1、2、3,正放置的四个正方形的面积依次是S1、S2、S3、S4,则S1+S2+S3+S4=_________。
7、如图1-4-63,矩形ABCD中,AB=8,BC=6,对角线AC上有一个动点P(不包括点A和点C).设AP=x,四边形PBCD的面积为y.
(1)写出y与x的函数关系,并确定自变量x范围.
(2)有人提出一个判断:“关于动点P,⊿PBC面积与ΔPAD面积之和为常数”.请你说明此判断是否正确,并说明理由
8、从等腰三角形底边上任意一点分别作两腰的平行线,与两腰所围成的平行四边形的周长等于三角形的( )
A.两腰长的和 B.周长的一半 C.周长 D.一腰长与底边长的和
9、如图1-4-68,在菱形ABCD中,∠BAD=80 ,AB的垂直平分线EF交对角线A C于点F、E为垂足,连结DF,则∠CDF等于( )
A.80° B.70° C.65° D.60°
10、直角梯形下底与一腰的夹角为60°,此腰与上底长都为8,则中位线长为_______.
11、(探究题)如图如图1-4-79,在矩形AB CD中,AB=12cm,BC=6cm,点P沿AB边从点A开始向点B以2cm/秒的速度移动;点Q沿DA边从点D开始向点A以1cm/秒的速度移动,如果P对同时出发,用t(秒)表示移动的时间(0<t<6),那么:
(1)当t为何值时,△QAP为等腰直角三角形?
(2)求四边形QAPC的面积,提出一个与计算结果有关的结论
A
B
C
D
E
F
x
y
O
A
B
C
第9题
C
D
E
H
A
B
F
第10题
同课章节目录
