华东师大版七上数学 5.1.1对顶角 课件(21张)
文档属性
| 名称 | 华东师大版七上数学 5.1.1对顶角 课件(21张) |

|
|
| 格式 | ppt | ||
| 文件大小 | 7.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-04 09:50:58 | ||
图片预览






文档简介
(共21张PPT)
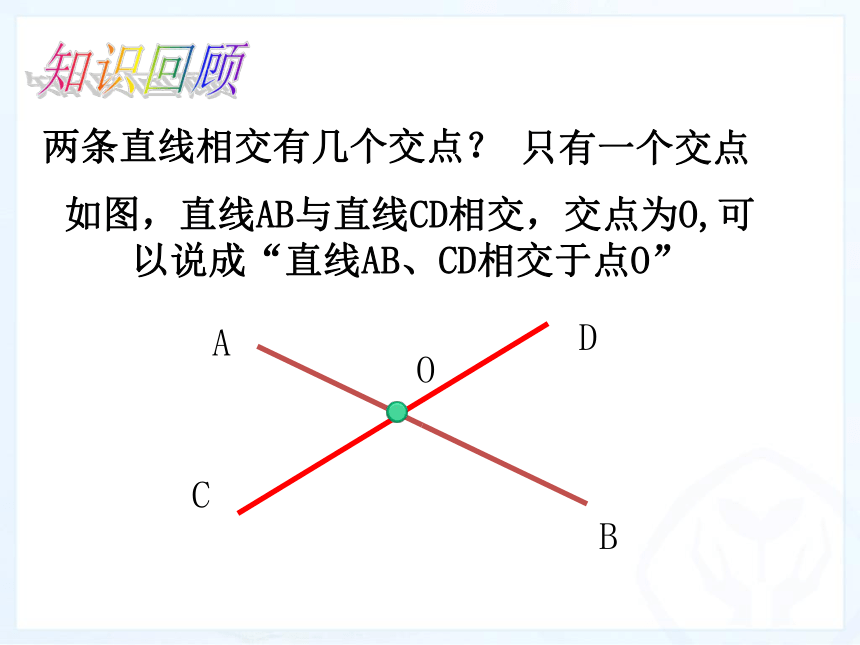
两条直线相交有几个交点?
只有一个交点
A
B
C
D
O
如图,直线AB与直线CD相交,交点为O,可以说成“直线AB、CD相交于点O”
观察这些图片,
你能否看到相交线、平行线?
这里有一把剪刀,握紧剪刀的把手,就能剪开物体,你能说出其中的道理吗?
如果把剪子的构造抽象成一个几何图形,会是什么样的图形?请你在笔记本上画出.
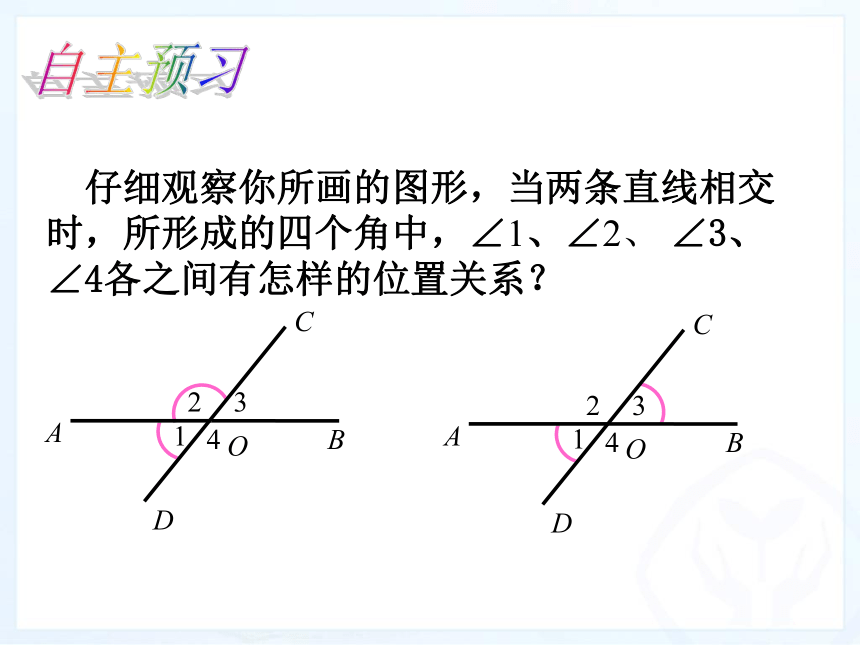
仔细观察你所画的图形,当两条直线相交时,所形成的四个角中,∠1、∠2、
∠3、
∠4各之间有怎样的位置关系?
A
B
C
D
O
1
2
3
4
A
B
C
D
O
1
2
3
4
A
B
C
D
4
3
2
1
)
)
)
)
O
两条直线相交形成了∠1、
∠2、
∠3和∠4.我们已经知道,有些角之间存在一定的关系,例如:
角
∠1和∠2
∠2和∠3
…
位置关系
相邻
相邻
…
数量关系
互补
互补
…
A
B
C
D
4
3
2
1
)
)
)
)
O
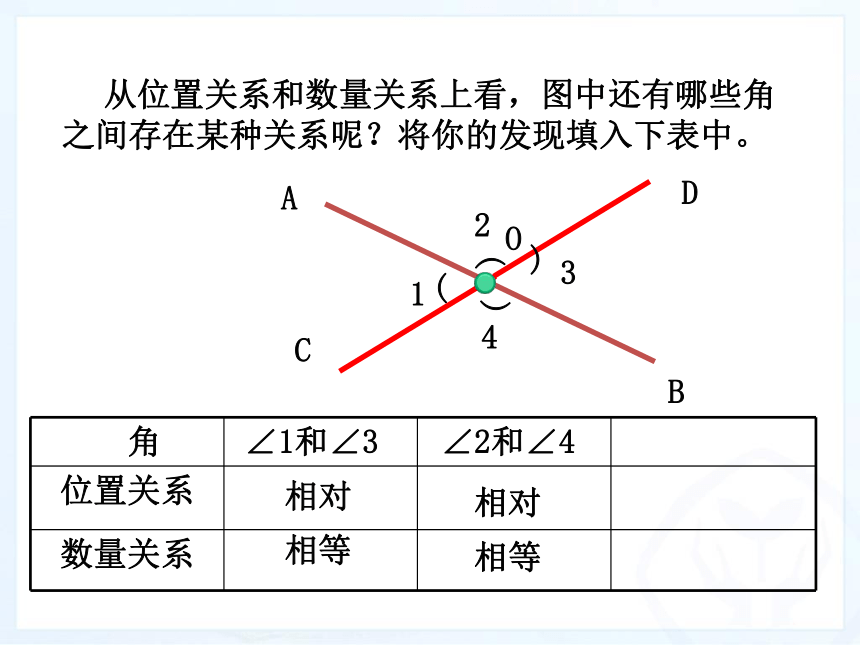
从位置关系和数量关系上看,图中还有哪些角之间存在某种关系呢?将你的发现填入下表中。
角
位置关系
数量关系
∠1和∠3
∠2和∠4
相对
相对
相等
相等
图中还有哪些对顶角?
A
B
C
D
O
1
2
3
4
对顶角的定义:
∠1和∠3有一个相同的顶点O,并且∠1的两边OA、OD分别与∠3的两边OB、OC互为反向延长线,我们把这样的两个角叫做对顶角.
A
B
C
D
4
3
2
1
)
)
)
)
O
每相邻的两个角有公共的顶点、有一条公共边,且另一条边在同一直线上,这样的两个角叫做邻补角.
∠1与∠2、∠2与∠3、∠1与∠4、∠3与∠4是邻补角。
不相邻的两个角有公共顶点,且一个角的两边是另一个角两边的反向延长线。这样的两个角叫做对顶角。
∠1与∠3,∠2与∠4是对顶角
1、下列各图中,∠1和∠2是邻补角吗?为什么?
(1)
(2)
(3)
1
2
1
1
2
2
1
2
(2)
(3)
(4)
2
1
(1)
1
2
(5)
1
2
1
2
2、下列各图中,∠1和∠2是对顶角吗?为什么?
3、请分别画出图中∠1的对顶角
和∠2的邻补角.
2
1
4、如图,三条直线AB
,CD
,EF相交于
点O,∠AOE的对顶角是
,
∠EOD的邻补角是
.
A
B
F
C
D
E
O
∠FOB
∠FOD、
∠COE
∠1与∠2有怎样的数量关系?
A
B
C
D
O
1
2
3
4
互
补
∠1与∠3有怎样的数量关系?
A
B
C
D
O
1
2
3
4
你是怎样得到的?
相
等
例1,
如图,直线a,b相交于点O,
∠1=
30°
,求∠2
,∠3
,∠4
的度数.
1
2
3
4
a
b
解:由邻补角定义,
O
∠2=180°-
∠1=180°-30°=150°,
∠3=180°-
∠2=180°-150°=30°
∠4=180°-
∠1=180°-30°=150°
由此可得:
∠1=∠3
,∠2
=∠4
你还能说出∠1=∠3的道理吗?
因为
∠1与∠2
互补,
∠3与∠2
互补
(邻补角的定义),
所以
∠1=∠3(同角的补角相等),
同理
∠2=∠4
.
A
B
C
D
O
1
2
3
4
请你用数学的语言写出这个过程.
结论:对顶角相等
例2
如图,直线AB、CD相交于点E,∠AEC=50°,
求∠BED的度数。
A
B
C
D
E
解:因为直线AB、CD相交与点E,
所以∠AEC与∠BED是对顶角。
根据对顶角相等,得
∠BED=∠AEC=50.
如图,直线a,b相交于点O,∠1
=
,
求∠2
,∠3
,∠4
的度数.
1
2
3
4
a
b
O
变式2
若∠2是∠1的
3.5倍,
求各个角的度数.
变式1
若∠1+∠3=
80
,
求各个角的度数.
变式3
若
1:
2
=
2:
7
,
求各个角的度数.
变式训练
(2)什么是对顶角?
对顶角有什么性质?
(1)什么是邻补角?
邻补角与补角有什么区别?
两条直线相交有几个交点?
只有一个交点
A
B
C
D
O
如图,直线AB与直线CD相交,交点为O,可以说成“直线AB、CD相交于点O”
观察这些图片,
你能否看到相交线、平行线?
这里有一把剪刀,握紧剪刀的把手,就能剪开物体,你能说出其中的道理吗?
如果把剪子的构造抽象成一个几何图形,会是什么样的图形?请你在笔记本上画出.
仔细观察你所画的图形,当两条直线相交时,所形成的四个角中,∠1、∠2、
∠3、
∠4各之间有怎样的位置关系?
A
B
C
D
O
1
2
3
4
A
B
C
D
O
1
2
3
4
A
B
C
D
4
3
2
1
)
)
)
)
O
两条直线相交形成了∠1、
∠2、
∠3和∠4.我们已经知道,有些角之间存在一定的关系,例如:
角
∠1和∠2
∠2和∠3
…
位置关系
相邻
相邻
…
数量关系
互补
互补
…
A
B
C
D
4
3
2
1
)
)
)
)
O
从位置关系和数量关系上看,图中还有哪些角之间存在某种关系呢?将你的发现填入下表中。
角
位置关系
数量关系
∠1和∠3
∠2和∠4
相对
相对
相等
相等
图中还有哪些对顶角?
A
B
C
D
O
1
2
3
4
对顶角的定义:
∠1和∠3有一个相同的顶点O,并且∠1的两边OA、OD分别与∠3的两边OB、OC互为反向延长线,我们把这样的两个角叫做对顶角.
A
B
C
D
4
3
2
1
)
)
)
)
O
每相邻的两个角有公共的顶点、有一条公共边,且另一条边在同一直线上,这样的两个角叫做邻补角.
∠1与∠2、∠2与∠3、∠1与∠4、∠3与∠4是邻补角。
不相邻的两个角有公共顶点,且一个角的两边是另一个角两边的反向延长线。这样的两个角叫做对顶角。
∠1与∠3,∠2与∠4是对顶角
1、下列各图中,∠1和∠2是邻补角吗?为什么?
(1)
(2)
(3)
1
2
1
1
2
2
1
2
(2)
(3)
(4)
2
1
(1)
1
2
(5)
1
2
1
2
2、下列各图中,∠1和∠2是对顶角吗?为什么?
3、请分别画出图中∠1的对顶角
和∠2的邻补角.
2
1
4、如图,三条直线AB
,CD
,EF相交于
点O,∠AOE的对顶角是
,
∠EOD的邻补角是
.
A
B
F
C
D
E
O
∠FOB
∠FOD、
∠COE
∠1与∠2有怎样的数量关系?
A
B
C
D
O
1
2
3
4
互
补
∠1与∠3有怎样的数量关系?
A
B
C
D
O
1
2
3
4
你是怎样得到的?
相
等
例1,
如图,直线a,b相交于点O,
∠1=
30°
,求∠2
,∠3
,∠4
的度数.
1
2
3
4
a
b
解:由邻补角定义,
O
∠2=180°-
∠1=180°-30°=150°,
∠3=180°-
∠2=180°-150°=30°
∠4=180°-
∠1=180°-30°=150°
由此可得:
∠1=∠3
,∠2
=∠4
你还能说出∠1=∠3的道理吗?
因为
∠1与∠2
互补,
∠3与∠2
互补
(邻补角的定义),
所以
∠1=∠3(同角的补角相等),
同理
∠2=∠4
.
A
B
C
D
O
1
2
3
4
请你用数学的语言写出这个过程.
结论:对顶角相等
例2
如图,直线AB、CD相交于点E,∠AEC=50°,
求∠BED的度数。
A
B
C
D
E
解:因为直线AB、CD相交与点E,
所以∠AEC与∠BED是对顶角。
根据对顶角相等,得
∠BED=∠AEC=50.
如图,直线a,b相交于点O,∠1
=
,
求∠2
,∠3
,∠4
的度数.
1
2
3
4
a
b
O
变式2
若∠2是∠1的
3.5倍,
求各个角的度数.
变式1
若∠1+∠3=
80
,
求各个角的度数.
变式3
若
1:
2
=
2:
7
,
求各个角的度数.
变式训练
(2)什么是对顶角?
对顶角有什么性质?
(1)什么是邻补角?
邻补角与补角有什么区别?
同课章节目录
- 第1章 走进数学世界
- 数学伴我们成长
- 人类离不开数学
- 人人都能学会数学
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数
- 2.4 绝对值
- 2.5 有理数的大小比较
- 2.6 有理数的加法
- 2.7 有理数的减法
- 2.8 有理数加减混合运算
- 2.9 有理数的乘法
- 2.10 有理数的除法
- 2.11 有理数的乘方
- 2.12 科学记数法
- 2.13 有理数的混合运算
- 2.14 近似数
- 2.15 用计算器进行计算
- 第3章 整式的加减
- 3.1 列代数式
- 3.2 代数式的值
- 3.3 整式
- 3.4 整式的加减
- 第4章 图形的初步认识
- 4.1 生活中的立体图形
- 4.2 立体图形的视图
- 4.3 立体图形的表面展开图
- 4.4 平面图形
- 4.5 最基本的图形——点和线
- 4.6 角
- 第5章 相交线与平行线
- 5.1 相交线
- 5.2 平行线
