26.1 二次函数课件-2021-2022学年华东师大版数学九年级下册(17张)
文档属性
| 名称 | 26.1 二次函数课件-2021-2022学年华东师大版数学九年级下册(17张) |

|
|
| 格式 | ppt | ||
| 文件大小 | 8.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-03 19:57:48 | ||
图片预览





文档简介
(共17张PPT)
26.1
二次函数
华东师大版
九年级下册
复习回顾
什么叫函数?
它有几种表示方法?
什么叫一次函数?
y
=
kx
+
b
的自变量是什么?常量是什么?为什么要有
k
≠
0
的条件?k
值对函数性质有什么影响?
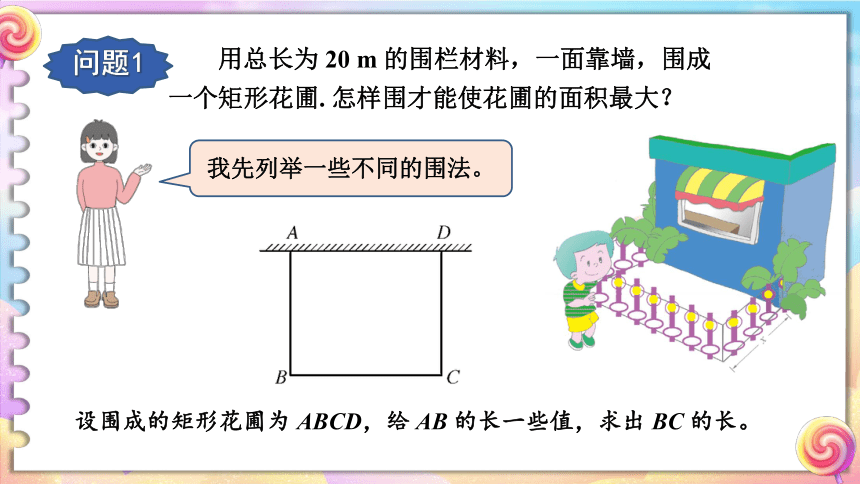
问题1
用总长为
20
m
的围栏材料,一面靠墙,围成一个矩形花圃.
怎样围才能使花圃的面积最大?
我先列举一些不同的围法。
设围成的矩形花圃为
ABCD,给
AB
的长一些值,求出
BC
的长。
18
18
16
32
14
42
10
50
8
48
6
42
4
32
2
18
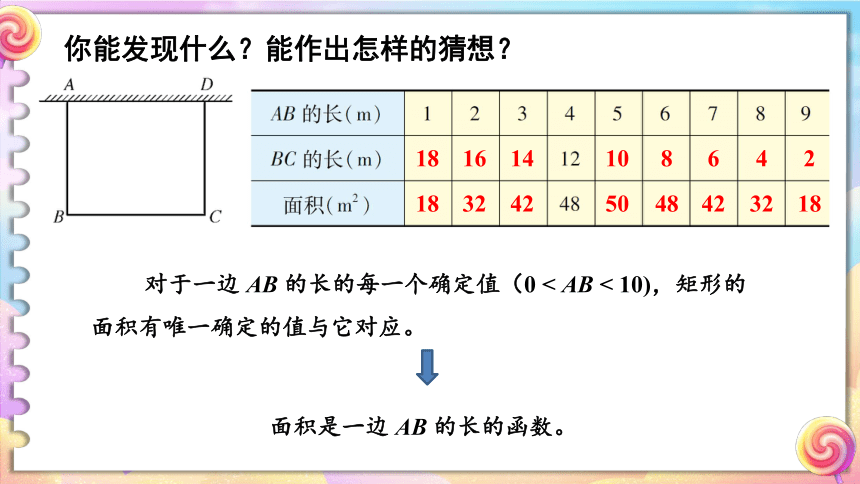
你能发现什么?能作出怎样的猜想?
对于一边
AB
的长的每一个确定值(0
<
AB
<
10),矩形的面积有唯一确定的值与它对应。
面积是一边
AB
的长的函数。
当AB
=
x
m
时,面积
y
等于多少?写出它们之间的关系式。
18
18
16
32
14
42
10
50
8
48
6
42
4
32
2
18
y
=
x
(
20-2x)
(
0
<
x
<
10
)
即
y
=
-2x2+20x
(
0
<
x
<
10
)
问题2
某商店将每件进价为
8
元的某种商品按每件
10
元出售,一天可售出
100
件.
该店想通过降低售价﹑增加销售量的办法来提高利润.
经过市场调查,发现这种商品每件每降价
0.1
元,每天的销售量可增加
10
件.
将这种商品的售价降低多少时,其每天的销售利润最大?
销售利润
=
(售价
-
进价)×销售量
设每件商品降价
x
元,销售该商品每天的利润为
y
元。
分析
(1)售价降低
x
元,每件利润为_____________元.
(10
-
x
-
8)
(2)售价降低
x
元时,共卖_____________件.
(100
+100x
)
(3)x
的取值范围是____________.
0
≤
x
≤
2
问题2
某商店将每件进价为
8
元的某种商品按每件
10
元出售,一天可售出
100
件.
该店想通过降低售价﹑增加销售量的办法来提高利润.
经过市场调查,发现这种商品每件每降价
0.1
元,每天的销售量可增加
10
件.
将这种商品的售价降低多少时,其每天的销售利润最大?
利润
y
与
x
之间有怎样的关系?
y
=
(10–x
-
8)(100
+
100x)
(0
≤
x
≤
2)
即
y
=
-100x2
+
100x
+
200
(0
≤
x
≤
2)
探
索
观察所得的两个函数关系式,它们有什么共同特点?
y
=
-2x2
+
20x
(
0
<
x
<
10
)
y
=
-100x2
+
100x
+
200
(0
≤
x
≤
2)
形如
y
=
ax2
+
bx
+
c(a、b、c是常数,a
≠
0)的函数叫做
x
的二次函数。
a
叫做二次项的系数,b
叫做一次项得系数,c
叫做常数项。
练
习
1.
已知直角三角形两条直角边的长的和为
10
cm.
(1)当它的一条直角边的长为
4.5
cm
时,求这个直角三角形的面积;
(2)设这个直角三角形的一条直角边的长为
x
cm,面积为
S
cm2,
求
S
与
x
之间的函数关系式.
(1)一条直角边长为
4.5
cm,
另一条直角边长为10-4.5
=
5.5cm.
面积
S
=
×4.5×5.5
=12.375(cm2)
【选自教材P4
练习
第1题】
练
习
1.
已知直角三角形两条直角边的长的和为
10
cm.
(1)当它的一条直角边的长为
4.5
cm
时,求这个直角三角形的面积;
(2)设这个直角三角形的一条直角边的长为
x
cm,面积为
S
cm2,
求
S
与
x
之间的函数关系式.
x
10-x
S
(2)S
=
×
x
(10-x)
=
-
x2
+
5x
(
0
<
x
<
10
)
练
习
2.
已知正方体的棱长为
x
cm,表面积为
S
cm2,体积为
V
cm3.
(1)分别写出
S
与x、V
与
x之间的函数关系式.
(2)这两个函数中,哪个是
x
的二次函数?
(1)S
=
6x2(cm2),
V
=
x3(cm3).
(2)S
=
6x2
是
x
的二次函数.
【选自教材P4
练习
第2题】
随堂演练
设圆柱的高为
6
cm,底面半径为
r
cm,底面周长为
C
cm,体积为
V
cm3
.
(1)分别写出
C
与
r、V
与
r、V
与
C
之间的函数关系式.
(2)这三个函数中,哪些是二次函数?
解:(1)C
=
2πr
,
V
=
6πr2
,V
=
.
(2)V
=
6πr2
是
V
关于
r
的二次函数;
V
=
是
V
关于
C
的二次函数.
【选自教材P4
习题26.1
第1题】
2.
正方形的边长为
4,当边长增加
x
时,面积增加
y
,求
y
与
x
之间的函数关系式.
这个函数是二次函数吗?
解:y
关于
x
的函数关系式为
y
=
(4
+
x)2-16
=
x2
+
8x,这个函数是二次函数.
【选自教材P4
习题26.1
第2题】
3.
已知二次函数
y
=
ax2
+
c,当
x
=
2
时,y
=
4;当
x
=
–
1
时,
y
=
-3.
求
a
、c
的值.
解:把
x
=
2,y
=
4;x
=
-1,y
=
-3
分别代入函数关系式
y
=
ax2
+
c中,得
解得
4a
+
c
=
4,
a
+
c
=
-3.
a
=
,
c
=
.
【选自教材P4
习题26.1
第3题】
4.
一条隧道的截面如图所示,它的上部是一个半圆,下部是一个矩形,
矩形的一边长为
2.5
m.
求:
(1)隧道截面的面积
S
(m2)与上部半圆的半径
r
(m)之间的函数关系式;
(2)当上部半圆的半径为
2
m
时的截面面积
(精确到
0.1
m2).
解:(1)观察图形,由题意可知
S
=
S半圆
+
S矩形
=
πr2
+
2r×2.5,
即
S
=
(2)当r
=
2
m
时,S
=
+
5×2
≈
16.3(m2)
【选自教材P4
习题26.1
第4题】
课堂小结
通过这节课的学习活动,你有什么收获?
形如
y
=
ax2
+
bx
+
c(a、b、c是常数,a
≠
0)的函数叫做
x
的二次函数。
a
叫做二次项的系数,b
叫做一次项得系数,c
叫做常数项。
1.从课后习题中选取;
2.完成练习册本课时的习题。
课后作业
26.1
二次函数
华东师大版
九年级下册
复习回顾
什么叫函数?
它有几种表示方法?
什么叫一次函数?
y
=
kx
+
b
的自变量是什么?常量是什么?为什么要有
k
≠
0
的条件?k
值对函数性质有什么影响?
问题1
用总长为
20
m
的围栏材料,一面靠墙,围成一个矩形花圃.
怎样围才能使花圃的面积最大?
我先列举一些不同的围法。
设围成的矩形花圃为
ABCD,给
AB
的长一些值,求出
BC
的长。
18
18
16
32
14
42
10
50
8
48
6
42
4
32
2
18
你能发现什么?能作出怎样的猜想?
对于一边
AB
的长的每一个确定值(0
<
AB
<
10),矩形的面积有唯一确定的值与它对应。
面积是一边
AB
的长的函数。
当AB
=
x
m
时,面积
y
等于多少?写出它们之间的关系式。
18
18
16
32
14
42
10
50
8
48
6
42
4
32
2
18
y
=
x
(
20-2x)
(
0
<
x
<
10
)
即
y
=
-2x2+20x
(
0
<
x
<
10
)
问题2
某商店将每件进价为
8
元的某种商品按每件
10
元出售,一天可售出
100
件.
该店想通过降低售价﹑增加销售量的办法来提高利润.
经过市场调查,发现这种商品每件每降价
0.1
元,每天的销售量可增加
10
件.
将这种商品的售价降低多少时,其每天的销售利润最大?
销售利润
=
(售价
-
进价)×销售量
设每件商品降价
x
元,销售该商品每天的利润为
y
元。
分析
(1)售价降低
x
元,每件利润为_____________元.
(10
-
x
-
8)
(2)售价降低
x
元时,共卖_____________件.
(100
+100x
)
(3)x
的取值范围是____________.
0
≤
x
≤
2
问题2
某商店将每件进价为
8
元的某种商品按每件
10
元出售,一天可售出
100
件.
该店想通过降低售价﹑增加销售量的办法来提高利润.
经过市场调查,发现这种商品每件每降价
0.1
元,每天的销售量可增加
10
件.
将这种商品的售价降低多少时,其每天的销售利润最大?
利润
y
与
x
之间有怎样的关系?
y
=
(10–x
-
8)(100
+
100x)
(0
≤
x
≤
2)
即
y
=
-100x2
+
100x
+
200
(0
≤
x
≤
2)
探
索
观察所得的两个函数关系式,它们有什么共同特点?
y
=
-2x2
+
20x
(
0
<
x
<
10
)
y
=
-100x2
+
100x
+
200
(0
≤
x
≤
2)
形如
y
=
ax2
+
bx
+
c(a、b、c是常数,a
≠
0)的函数叫做
x
的二次函数。
a
叫做二次项的系数,b
叫做一次项得系数,c
叫做常数项。
练
习
1.
已知直角三角形两条直角边的长的和为
10
cm.
(1)当它的一条直角边的长为
4.5
cm
时,求这个直角三角形的面积;
(2)设这个直角三角形的一条直角边的长为
x
cm,面积为
S
cm2,
求
S
与
x
之间的函数关系式.
(1)一条直角边长为
4.5
cm,
另一条直角边长为10-4.5
=
5.5cm.
面积
S
=
×4.5×5.5
=12.375(cm2)
【选自教材P4
练习
第1题】
练
习
1.
已知直角三角形两条直角边的长的和为
10
cm.
(1)当它的一条直角边的长为
4.5
cm
时,求这个直角三角形的面积;
(2)设这个直角三角形的一条直角边的长为
x
cm,面积为
S
cm2,
求
S
与
x
之间的函数关系式.
x
10-x
S
(2)S
=
×
x
(10-x)
=
-
x2
+
5x
(
0
<
x
<
10
)
练
习
2.
已知正方体的棱长为
x
cm,表面积为
S
cm2,体积为
V
cm3.
(1)分别写出
S
与x、V
与
x之间的函数关系式.
(2)这两个函数中,哪个是
x
的二次函数?
(1)S
=
6x2(cm2),
V
=
x3(cm3).
(2)S
=
6x2
是
x
的二次函数.
【选自教材P4
练习
第2题】
随堂演练
设圆柱的高为
6
cm,底面半径为
r
cm,底面周长为
C
cm,体积为
V
cm3
.
(1)分别写出
C
与
r、V
与
r、V
与
C
之间的函数关系式.
(2)这三个函数中,哪些是二次函数?
解:(1)C
=
2πr
,
V
=
6πr2
,V
=
.
(2)V
=
6πr2
是
V
关于
r
的二次函数;
V
=
是
V
关于
C
的二次函数.
【选自教材P4
习题26.1
第1题】
2.
正方形的边长为
4,当边长增加
x
时,面积增加
y
,求
y
与
x
之间的函数关系式.
这个函数是二次函数吗?
解:y
关于
x
的函数关系式为
y
=
(4
+
x)2-16
=
x2
+
8x,这个函数是二次函数.
【选自教材P4
习题26.1
第2题】
3.
已知二次函数
y
=
ax2
+
c,当
x
=
2
时,y
=
4;当
x
=
–
1
时,
y
=
-3.
求
a
、c
的值.
解:把
x
=
2,y
=
4;x
=
-1,y
=
-3
分别代入函数关系式
y
=
ax2
+
c中,得
解得
4a
+
c
=
4,
a
+
c
=
-3.
a
=
,
c
=
.
【选自教材P4
习题26.1
第3题】
4.
一条隧道的截面如图所示,它的上部是一个半圆,下部是一个矩形,
矩形的一边长为
2.5
m.
求:
(1)隧道截面的面积
S
(m2)与上部半圆的半径
r
(m)之间的函数关系式;
(2)当上部半圆的半径为
2
m
时的截面面积
(精确到
0.1
m2).
解:(1)观察图形,由题意可知
S
=
S半圆
+
S矩形
=
πr2
+
2r×2.5,
即
S
=
(2)当r
=
2
m
时,S
=
+
5×2
≈
16.3(m2)
【选自教材P4
习题26.1
第4题】
课堂小结
通过这节课的学习活动,你有什么收获?
形如
y
=
ax2
+
bx
+
c(a、b、c是常数,a
≠
0)的函数叫做
x
的二次函数。
a
叫做二次项的系数,b
叫做一次项得系数,c
叫做常数项。
1.从课后习题中选取;
2.完成练习册本课时的习题。
课后作业
