第26章二次函数复习课件-2021-2022学年华东师大版数学九年级下册(31张)
文档属性
| 名称 | 第26章二次函数复习课件-2021-2022学年华东师大版数学九年级下册(31张) |

|
|
| 格式 | ppt | ||
| 文件大小 | 8.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-03 00:00:00 | ||
图片预览







文档简介
(共31张PPT)
章末复习
华东师大版
九年级下册
实际问题
二次函数的图象
二次函数
二次函数的性质
二次函数的应用
知识结构
释疑解惑
1.二次函数解析式的二种表示方法:
(1)顶点式:______________________
(2)一般式:______________________
y
=
a(x
-
h)2
+
k(a
≠
0)
y
=
ax2
+
bx
+
c(a
≠
0)
2.填表:
y
轴
(0,0)
y
轴
(0,k)
x
=
h
(h,0)
x
=
h
(h,k)
向上
向下
3.
二次函数
y
=
ax2+
bx
+
c,当
a
>
0
时,在对称轴右侧,
y
随
x
的增大而______,在对称轴左侧,
y
随
x
的增大
而_______;当
a
<
0
时,在对称轴右侧,y
随
x
的增大
而_______,在对称轴左侧,y
随
x
的增大而______.
增大
减小
减小
增大
4.
抛物线
y
=
ax2+
bx
+
c,当
a
>
0
时图象有最_____点,
此时函数有最____值_______;
当
a
<
0
时图象有最_____点,此时函数有最____值
________.
低
小
高
大
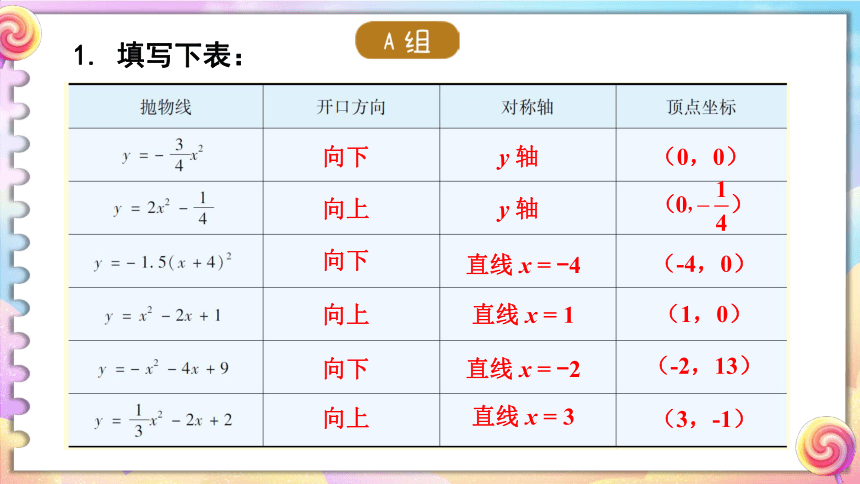
1.
填写下表:
向下
y
轴
(0,0)
向上
y
轴
向下
直线
x
=
-4
(-4,0)
向上
直线
x
=
1
(1,0)
向下
直线
x
=
-2
(-2,13)
向上
直线
x
=
3
(3,-1)
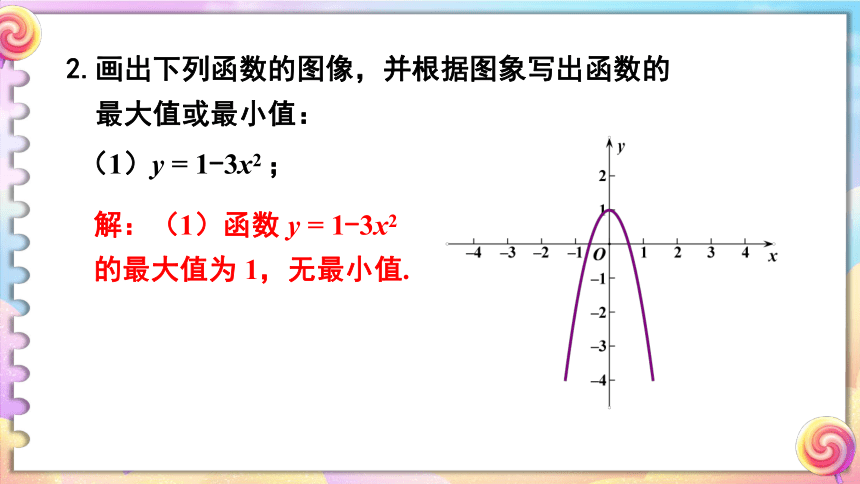
2.画出下列函数的图像,并根据图象写出函数的
最大值或最小值:
(1)y
=
1-3x2
;
解:(1)函数
y
=
1-3x2
的最大值为
1,无最小值.
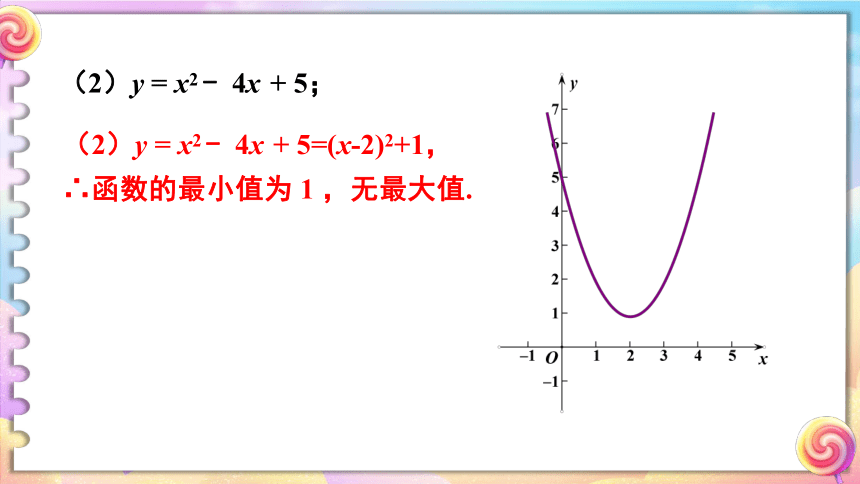
(2)y
=
x2
-
4x
+
5;
(2)y
=
x2
-
4x
+
5=(x-2)2+1,
∴函数的最小值为
1
,无最大值.
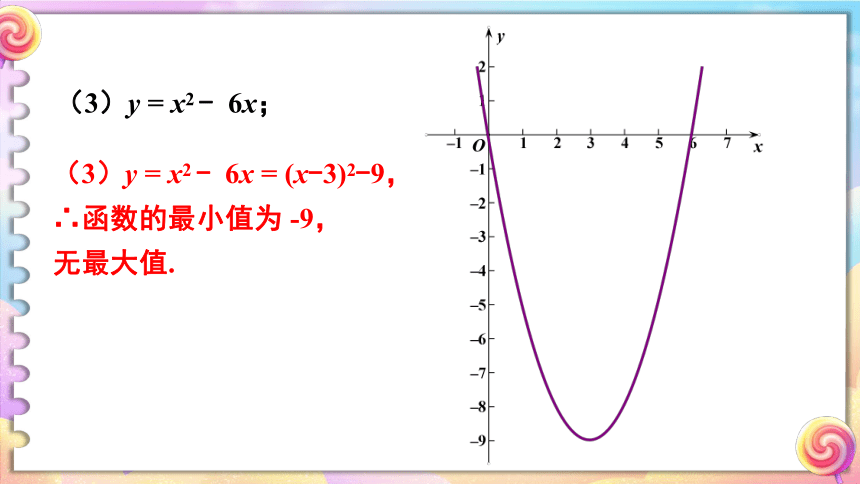
(3)y
=
x2
-
6x;
(3)y
=
x2
-
6x
=
(x-3)2-9,
∴函数的最小值为
-9,
无最大值.
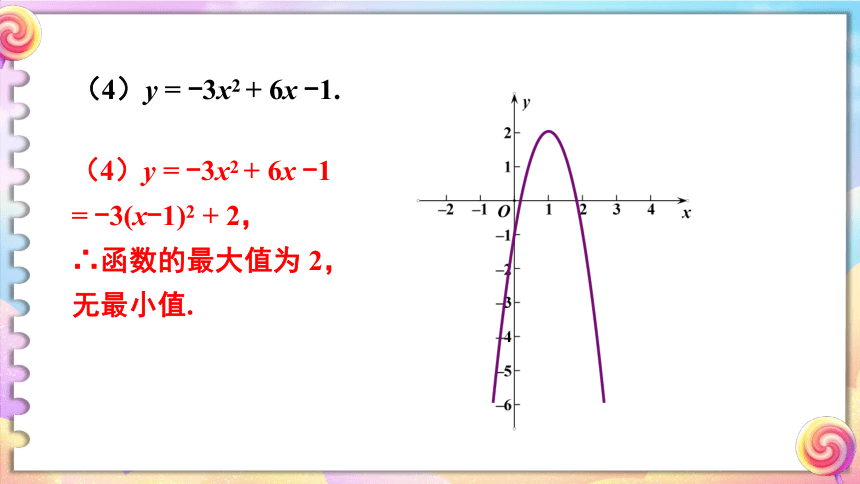
(4)y
=
-3x2
+
6x
-1.
(4)y
=
-3x2
+
6x
-1
=
-3(x-1)2
+
2,
∴函数的最大值为
2,
无最小值.
3.通过配方,写出下列抛物线的开口方向、对称轴
和顶点坐标:
(1)y
=
x2
-2x-4;
(2)y
=1
+
6x
-x2
;
解:(1)y
=
x2
-2x-4
=
(x-1)2-5,
∴抛物线开口向上,对称轴是直线
x=1,顶点坐标是(1,-5).
(2)y
=1
+
6x
-x2
=
-(x-3)2
+
10,
∴抛物线开口向下,对称轴是直线
x
=
3,顶点坐标是(3,10).
(3)y
=
-x2
+
4x;
(3)y
=
-x2
+
4x;=
-(x-2)2
+
4,
∴抛物线开口向下,对称轴是直线
x
=
2,顶点坐标是(2,4).
∴抛物线开口向上,对称轴是直线
x
=
2,顶点坐标是(2,3).
4.已知函数
y
=
2x2-3x-2,解答下列问题:
(1)画出函数的图象;
(2)观察图象,说出
x
取哪些值时,函数的值为
0.
解:(1)函数图象如图所示.
(2)当
x
取
或
2
时,函数的值为
0.
5.填空:
(1)抛物线
y
=
x2-3x
+2
与
y
轴的交点坐标是______,与
x
轴的交点坐标是_______________;
(2)抛物线
y
=
-2x2
+
5x
-3
与
y
轴的交点坐标是_____,与
x
轴的交点坐标是___________________.
(0,2)
(1,0)和(2,0)
(0,-3)
(
,0)和(1,0)
6.
已知抛物线
y
=
ax2
+
x
+
2
经过点
(-1,0),求
a
的值,
并写出这条抛物线的顶点坐标.
解:
∵抛物线过点
(-1,0)
,∴a-1+2
=
0,解得
a
=
-1.
∴函数关系式为
y
=
-x2
+
x
+
2.
配方,得
∴抛物线的顶点坐标为
.
7.
求图象为下列抛物线的二次函数的表达式:
(1)抛物线经过
(2,0)、(0,-2)
和
(-2,3)
三点;
(2)抛物线的顶点坐标是
(6,-4),
且抛物线经过点(4,-2).
解:
(1)设二次函数关系式为
y
=
ax2
+
bx
+
c(a
≠
0).
4a
+
2b
+
c
=
0,
c=-2,
4a-2b+c=3.
∴
解得
∴函数关系式为
.
7.
求图象为下列抛物线的二次函数的表达式:
(1)抛物线经过
(2,0)、(0,-2)
和
(-2,3)
三点;
(2)抛物线的顶点坐标是
(6,-4),
且抛物线经过点(4,-2).
(2)设函数关系式为
y
=
a(x-h)2
+
k
(a
≠
0).∵抛物线顶点为(6,-4),且过点(4,-2).
h
=
6,
k=-4,
-2
=
a(4
-
h)2
+
k.
∴
解得
∴函数关系式为
.
8.
已知二次函数
y
=
(x
-
2)2-1,解答下列问题:
(1)先确定其图象的开口方向、对称轴和顶点坐标,再画出图象.
(2)观察图象确定:
x
取什么值时,①y
=
0;②y
>
0;③y
<0.
解:(1)二次函数y
=
(x-2)2-1
的图象开口向上,对称轴是直线
x=2,顶点坐标是
(2,-1),
(2)①当
x
取
1
或
3
时,y=0;
②当x
>
3或
x
<
1时,y>0;
③当
19.
将抛物线
y
=
3x2
经过怎样的平移可以得到下列函数的图象?
解:(1)将
y
=
3x2
的图象向下平移
个单位,得到
(2)将
y
=
3x2
的图象向右平移
个单位,得到
9.
将抛物线
y
=
3x2
经过怎样的平移可以得到下列函数的图象?
(3)将
y
=
3x2
的图象向右平移
个单位,再向上平移
4
个单位,得到
(4)
y
=
3x2-6x
=
3(x-1)2-3
,∴将
y
=
3x2
的图象向右平移
1
个单位,再向下平移
3
个单位,得到
y
=
3x2-6x
.
10.
观察下面表格:
(1)求
a、b、c
的值,并在表内的空格中填上正确的数;
(2)设
y=ax2
+
bx
+
c,求这个二次函数的图象的对称轴与顶点坐标.
解:
(1)由表格知
a
=
1,
c
=3,
4a+2b+c=3.
a
=
1,
b
=-2,
c=3.
解得
∴当x=0时,ax2=0;当x=2时,ax2=4;当x=1时,ax2+bx+c
=
2.
10.
观察下面表格:
(1)求
a、b、c
的值,并在表内的空格中填上正确的数;
(2)设
y=ax2
+
bx
+
c,求这个二次函数的图象的对称轴与顶点坐标.
(2)由(1)知
y
=
x2-2x
+
3.
配方,得
y
=
(x-1)2
+
2.
∴这个二次函数的图象的顶点坐标为(1,2),对称轴是直线
x
=
1.
11.若抛物线
y=x2-x-2
经过点
A(3,a)
和点
B(b,0),求点
A、B
的坐标.
解:抛物线经过点
A(3,a)、B(b,0),
∴
9-3-2=
a,
b2-b-2
=0,
a
=
4,
b
=
-1或2.
解得
∴点
A
的坐标是(3,4)、点B
的坐标是
(2,0)或(-1,0),
12.
行驶中的汽车刹车后,由于惯性还会继续向前滑行一段距离,这段距离称为“刹车距离”.
某车的刹车距离
s(m)
与车速
x
(km/h)
之间有如下的函数关系:
s
=
0.01x
+
0.002x2.
现该车在限速
120
km/h
的高速公路上出了交通事故,事后测得其刹车距离为35.1
m.
请推测刹车前,汽车是否超速?
解:根据题意有:35.1
=
0.01x
+
0.002x2.
解得
x1
=
130,x2
=
-135(舍)
∵x
=
130
>
120.
∴在刹车前,该车已超速.
13.
已知二次函数的图象满足下列条件,求它的函数表达式:
(1)经过原点和点(-1,3),对称轴为直线
x=4;
(2)经过点(1,1)、(-2,1)和(2,-3).
解:(1)由题意,可将函数设为
y
=
a(x
-
4)2
-
16a.
(a≠0)
∴函数表达式为
∵经过点(-1,3),将
x
=
-1.
y
=
3
代入解得
.
13.
已知二次函数的图象满足下列条件,求它的函数表达式:
(1)经过原点和点(-1,3),对称轴为直线
x=4;
(2)经过点(1,1)、(-2,1)和(2,-3).
(2)设函数为
y
=
ax2
+
bx
+
c
(a≠0)
分别将(1,1),(-2,1)和(2,-3)代入得.
1
=
a+b+c,
1
=4a-2b+c,
-3=4a+2b+c.
a
=
-1,
b
=-1,
c=3.
解得
∴函数表达式为
y
=
-x2
-x
+
3
14.
如图,有一个横截面边缘为抛物线的水泥门洞.门洞内的地面宽度为
8
m,两侧距地面
4
m
高处各有一盏灯,两灯间的水平距离为
6
m.
求这个门洞的高度.
(精确到0.l
m)
解:把门洞放在如图所示的直角坐标系中,根据题意可知,点
A、B、C
的坐标分别为(8,0),(1,4),(7,4).设抛物线的函数关系式为
y=ax2+bx+c
(a≠0)
64a+8b+c=0
a+b+c=4
49a+7b+c=4
则有方程组
解得
∴
当
x
=
4
时,
答:这个门洞高约为9.1m
B
A
C
15.如图,一位篮球运动员在距离篮圈中心水平距离
4
m
处跳起投篮,球沿一条抛物线运动,当球运动的水平距离为
2.5
m
时,达到最大高度
3.5
m,然后准确落入篮框内
.已知篮圈中心距离地面高度为
3.05
m,试解答下列问题:
(1)建立图中所示的平面直角坐标系,求抛物线所对应的函数表达式.
(2)这次跳投时,球出手处离地面多高?
解:
(1)设函数关系式为
y
=
ax
+
k(a
≠
0).由图可知函数图象经过点(0,
3.5),(1.5,
3.05),
02·a
+
k
=
3.5,
a·1.52
+
k
=
3.05,
∴
a
=
-0.2,
k
=
3.5,
解得
∴抛物线的函数表达式为
y
=
-0.2x2
+
3.5
15.如图,一位篮球运动员在距离篮圈中心水平距离
4
m
处跳起投篮,球沿一条抛物线运动,当球运动的水平距离为
2.5
m
时,达到最大高度
3.5
m,然后准确落入篮框内
.已知篮圈中心距离地面高度为
3.05
m,试解答下列问题:
(1)建立图中所示的平面直角坐标系,求抛物线所对应的函数表达式.
(2)这次跳投时,球出手处离地面多高?
(2)当
x=-2.5
时,y=2.25.
∴球出手处离地面
2.25
m.
1.从课后习题中选取;
2.完成练习册本课时的习题。
课后作业
章末复习
华东师大版
九年级下册
实际问题
二次函数的图象
二次函数
二次函数的性质
二次函数的应用
知识结构
释疑解惑
1.二次函数解析式的二种表示方法:
(1)顶点式:______________________
(2)一般式:______________________
y
=
a(x
-
h)2
+
k(a
≠
0)
y
=
ax2
+
bx
+
c(a
≠
0)
2.填表:
y
轴
(0,0)
y
轴
(0,k)
x
=
h
(h,0)
x
=
h
(h,k)
向上
向下
3.
二次函数
y
=
ax2+
bx
+
c,当
a
>
0
时,在对称轴右侧,
y
随
x
的增大而______,在对称轴左侧,
y
随
x
的增大
而_______;当
a
<
0
时,在对称轴右侧,y
随
x
的增大
而_______,在对称轴左侧,y
随
x
的增大而______.
增大
减小
减小
增大
4.
抛物线
y
=
ax2+
bx
+
c,当
a
>
0
时图象有最_____点,
此时函数有最____值_______;
当
a
<
0
时图象有最_____点,此时函数有最____值
________.
低
小
高
大
1.
填写下表:
向下
y
轴
(0,0)
向上
y
轴
向下
直线
x
=
-4
(-4,0)
向上
直线
x
=
1
(1,0)
向下
直线
x
=
-2
(-2,13)
向上
直线
x
=
3
(3,-1)
2.画出下列函数的图像,并根据图象写出函数的
最大值或最小值:
(1)y
=
1-3x2
;
解:(1)函数
y
=
1-3x2
的最大值为
1,无最小值.
(2)y
=
x2
-
4x
+
5;
(2)y
=
x2
-
4x
+
5=(x-2)2+1,
∴函数的最小值为
1
,无最大值.
(3)y
=
x2
-
6x;
(3)y
=
x2
-
6x
=
(x-3)2-9,
∴函数的最小值为
-9,
无最大值.
(4)y
=
-3x2
+
6x
-1.
(4)y
=
-3x2
+
6x
-1
=
-3(x-1)2
+
2,
∴函数的最大值为
2,
无最小值.
3.通过配方,写出下列抛物线的开口方向、对称轴
和顶点坐标:
(1)y
=
x2
-2x-4;
(2)y
=1
+
6x
-x2
;
解:(1)y
=
x2
-2x-4
=
(x-1)2-5,
∴抛物线开口向上,对称轴是直线
x=1,顶点坐标是(1,-5).
(2)y
=1
+
6x
-x2
=
-(x-3)2
+
10,
∴抛物线开口向下,对称轴是直线
x
=
3,顶点坐标是(3,10).
(3)y
=
-x2
+
4x;
(3)y
=
-x2
+
4x;=
-(x-2)2
+
4,
∴抛物线开口向下,对称轴是直线
x
=
2,顶点坐标是(2,4).
∴抛物线开口向上,对称轴是直线
x
=
2,顶点坐标是(2,3).
4.已知函数
y
=
2x2-3x-2,解答下列问题:
(1)画出函数的图象;
(2)观察图象,说出
x
取哪些值时,函数的值为
0.
解:(1)函数图象如图所示.
(2)当
x
取
或
2
时,函数的值为
0.
5.填空:
(1)抛物线
y
=
x2-3x
+2
与
y
轴的交点坐标是______,与
x
轴的交点坐标是_______________;
(2)抛物线
y
=
-2x2
+
5x
-3
与
y
轴的交点坐标是_____,与
x
轴的交点坐标是___________________.
(0,2)
(1,0)和(2,0)
(0,-3)
(
,0)和(1,0)
6.
已知抛物线
y
=
ax2
+
x
+
2
经过点
(-1,0),求
a
的值,
并写出这条抛物线的顶点坐标.
解:
∵抛物线过点
(-1,0)
,∴a-1+2
=
0,解得
a
=
-1.
∴函数关系式为
y
=
-x2
+
x
+
2.
配方,得
∴抛物线的顶点坐标为
.
7.
求图象为下列抛物线的二次函数的表达式:
(1)抛物线经过
(2,0)、(0,-2)
和
(-2,3)
三点;
(2)抛物线的顶点坐标是
(6,-4),
且抛物线经过点(4,-2).
解:
(1)设二次函数关系式为
y
=
ax2
+
bx
+
c(a
≠
0).
4a
+
2b
+
c
=
0,
c=-2,
4a-2b+c=3.
∴
解得
∴函数关系式为
.
7.
求图象为下列抛物线的二次函数的表达式:
(1)抛物线经过
(2,0)、(0,-2)
和
(-2,3)
三点;
(2)抛物线的顶点坐标是
(6,-4),
且抛物线经过点(4,-2).
(2)设函数关系式为
y
=
a(x-h)2
+
k
(a
≠
0).∵抛物线顶点为(6,-4),且过点(4,-2).
h
=
6,
k=-4,
-2
=
a(4
-
h)2
+
k.
∴
解得
∴函数关系式为
.
8.
已知二次函数
y
=
(x
-
2)2-1,解答下列问题:
(1)先确定其图象的开口方向、对称轴和顶点坐标,再画出图象.
(2)观察图象确定:
x
取什么值时,①y
=
0;②y
>
0;③y
<0.
解:(1)二次函数y
=
(x-2)2-1
的图象开口向上,对称轴是直线
x=2,顶点坐标是
(2,-1),
(2)①当
x
取
1
或
3
时,y=0;
②当x
>
3或
x
<
1时,y>0;
③当
1
将抛物线
y
=
3x2
经过怎样的平移可以得到下列函数的图象?
解:(1)将
y
=
3x2
的图象向下平移
个单位,得到
(2)将
y
=
3x2
的图象向右平移
个单位,得到
9.
将抛物线
y
=
3x2
经过怎样的平移可以得到下列函数的图象?
(3)将
y
=
3x2
的图象向右平移
个单位,再向上平移
4
个单位,得到
(4)
y
=
3x2-6x
=
3(x-1)2-3
,∴将
y
=
3x2
的图象向右平移
1
个单位,再向下平移
3
个单位,得到
y
=
3x2-6x
.
10.
观察下面表格:
(1)求
a、b、c
的值,并在表内的空格中填上正确的数;
(2)设
y=ax2
+
bx
+
c,求这个二次函数的图象的对称轴与顶点坐标.
解:
(1)由表格知
a
=
1,
c
=3,
4a+2b+c=3.
a
=
1,
b
=-2,
c=3.
解得
∴当x=0时,ax2=0;当x=2时,ax2=4;当x=1时,ax2+bx+c
=
2.
10.
观察下面表格:
(1)求
a、b、c
的值,并在表内的空格中填上正确的数;
(2)设
y=ax2
+
bx
+
c,求这个二次函数的图象的对称轴与顶点坐标.
(2)由(1)知
y
=
x2-2x
+
3.
配方,得
y
=
(x-1)2
+
2.
∴这个二次函数的图象的顶点坐标为(1,2),对称轴是直线
x
=
1.
11.若抛物线
y=x2-x-2
经过点
A(3,a)
和点
B(b,0),求点
A、B
的坐标.
解:抛物线经过点
A(3,a)、B(b,0),
∴
9-3-2=
a,
b2-b-2
=0,
a
=
4,
b
=
-1或2.
解得
∴点
A
的坐标是(3,4)、点B
的坐标是
(2,0)或(-1,0),
12.
行驶中的汽车刹车后,由于惯性还会继续向前滑行一段距离,这段距离称为“刹车距离”.
某车的刹车距离
s(m)
与车速
x
(km/h)
之间有如下的函数关系:
s
=
0.01x
+
0.002x2.
现该车在限速
120
km/h
的高速公路上出了交通事故,事后测得其刹车距离为35.1
m.
请推测刹车前,汽车是否超速?
解:根据题意有:35.1
=
0.01x
+
0.002x2.
解得
x1
=
130,x2
=
-135(舍)
∵x
=
130
>
120.
∴在刹车前,该车已超速.
13.
已知二次函数的图象满足下列条件,求它的函数表达式:
(1)经过原点和点(-1,3),对称轴为直线
x=4;
(2)经过点(1,1)、(-2,1)和(2,-3).
解:(1)由题意,可将函数设为
y
=
a(x
-
4)2
-
16a.
(a≠0)
∴函数表达式为
∵经过点(-1,3),将
x
=
-1.
y
=
3
代入解得
.
13.
已知二次函数的图象满足下列条件,求它的函数表达式:
(1)经过原点和点(-1,3),对称轴为直线
x=4;
(2)经过点(1,1)、(-2,1)和(2,-3).
(2)设函数为
y
=
ax2
+
bx
+
c
(a≠0)
分别将(1,1),(-2,1)和(2,-3)代入得.
1
=
a+b+c,
1
=4a-2b+c,
-3=4a+2b+c.
a
=
-1,
b
=-1,
c=3.
解得
∴函数表达式为
y
=
-x2
-x
+
3
14.
如图,有一个横截面边缘为抛物线的水泥门洞.门洞内的地面宽度为
8
m,两侧距地面
4
m
高处各有一盏灯,两灯间的水平距离为
6
m.
求这个门洞的高度.
(精确到0.l
m)
解:把门洞放在如图所示的直角坐标系中,根据题意可知,点
A、B、C
的坐标分别为(8,0),(1,4),(7,4).设抛物线的函数关系式为
y=ax2+bx+c
(a≠0)
64a+8b+c=0
a+b+c=4
49a+7b+c=4
则有方程组
解得
∴
当
x
=
4
时,
答:这个门洞高约为9.1m
B
A
C
15.如图,一位篮球运动员在距离篮圈中心水平距离
4
m
处跳起投篮,球沿一条抛物线运动,当球运动的水平距离为
2.5
m
时,达到最大高度
3.5
m,然后准确落入篮框内
.已知篮圈中心距离地面高度为
3.05
m,试解答下列问题:
(1)建立图中所示的平面直角坐标系,求抛物线所对应的函数表达式.
(2)这次跳投时,球出手处离地面多高?
解:
(1)设函数关系式为
y
=
ax
+
k(a
≠
0).由图可知函数图象经过点(0,
3.5),(1.5,
3.05),
02·a
+
k
=
3.5,
a·1.52
+
k
=
3.05,
∴
a
=
-0.2,
k
=
3.5,
解得
∴抛物线的函数表达式为
y
=
-0.2x2
+
3.5
15.如图,一位篮球运动员在距离篮圈中心水平距离
4
m
处跳起投篮,球沿一条抛物线运动,当球运动的水平距离为
2.5
m
时,达到最大高度
3.5
m,然后准确落入篮框内
.已知篮圈中心距离地面高度为
3.05
m,试解答下列问题:
(1)建立图中所示的平面直角坐标系,求抛物线所对应的函数表达式.
(2)这次跳投时,球出手处离地面多高?
(2)当
x=-2.5
时,y=2.25.
∴球出手处离地面
2.25
m.
1.从课后习题中选取;
2.完成练习册本课时的习题。
课后作业
