沪科版九年级数学第二学期期中测试卷(word版含答案)
文档属性
| 名称 | 沪科版九年级数学第二学期期中测试卷(word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 178.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-04 14:56:56 | ||
图片预览



文档简介
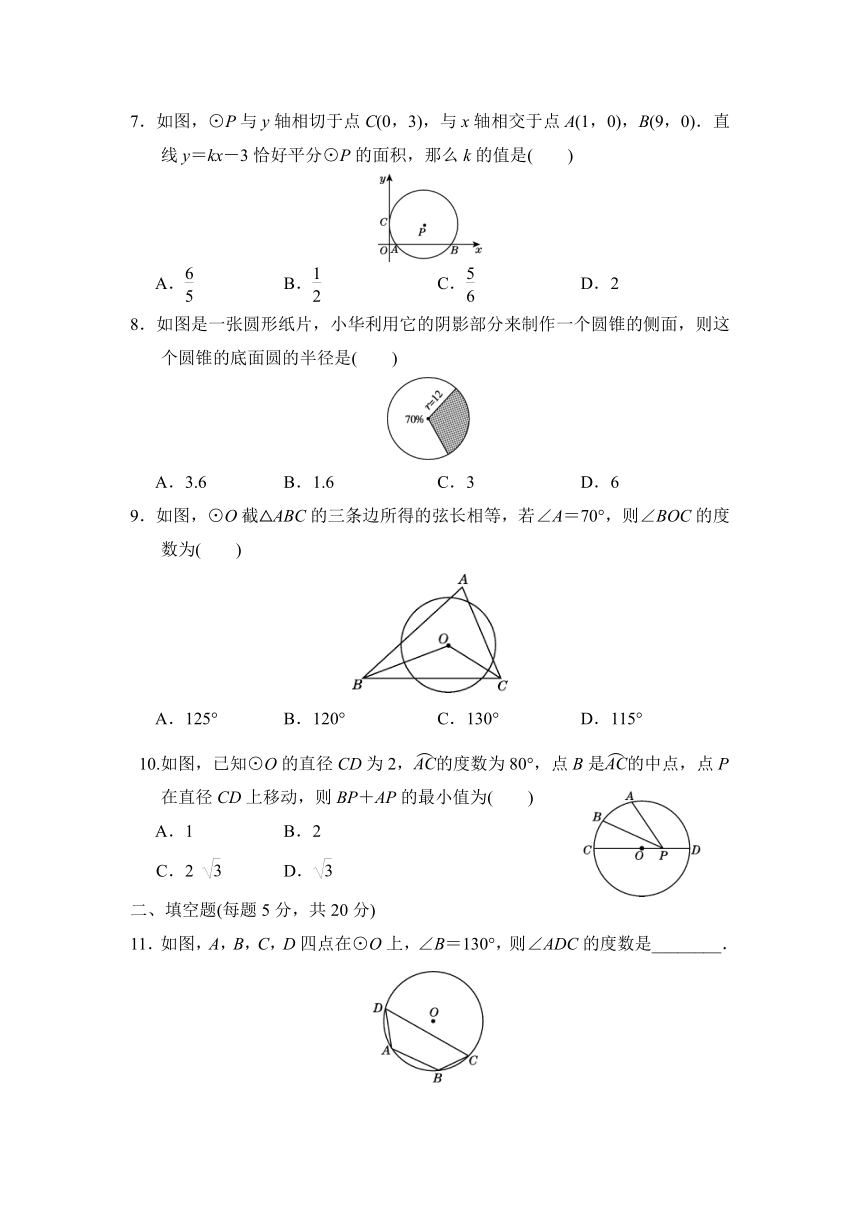
第二学期期中测试卷
一、选择题(每题4分,共40分)
1.在下列四个图案中,不是中心对称图形的是( )
2.已知⊙O的半径为6,点P在⊙O内,则OP的长可能是( )
A.5
B.6
C.7
D.8
3.已知⊙O的直径为12
cm,圆心到直线l的距离为5
cm,则直线l与⊙O的公共点的个数为( )
A.2
B.1
C.0
D.无法确定
4.如图,在⊙O中,∠AOB=70°,点C,D是⊙O上任意两点,则∠C+∠D的度数是( )
A.70°
B.80°
C.90°
D.140°
5.如图,在⊙O中,弦AB的长为6
cm,圆心O到AB的距离为4
cm,则⊙O的半径长为( )
A.3
cm
B.4
cm
C.5
cm
D.6
cm
6.如图,⊙O是△ABC的内切圆,切点分别是D,E,F,已知∠A=100°,∠C=30°,则∠DFE的度数是( )
A.55°
B.60°
C.65°
D.70°
7.如图,⊙P与y轴相切于点C(0,3),与x轴相交于点A(1,0),B(9,0).直线y=kx-3恰好平分⊙P的面积,那么k的值是( )
A.
B.
C.
D.2
8.如图是一张圆形纸片,小华利用它的阴影部分来制作一个圆锥的侧面,则这个圆锥的底面圆的半径是( )
A.3.6
B.1.6
C.3
D.6
9.如图,⊙O截△ABC的三条边所得的弦长相等,若∠A=70°,则∠BOC的度数为( )
A.125°
B.120°
C.130°
D.115°
10.如图,已知⊙O的直径CD为2,的度数为80°,点B是的中点,点P在直径CD上移动,则BP+AP的最小值为( )
A.1
B.2
C.2
D.
二、填空题(每题5分,共20分)
11.如图,A,B,C,D四点在⊙O上,∠B=130°,则∠ADC的度数是________.
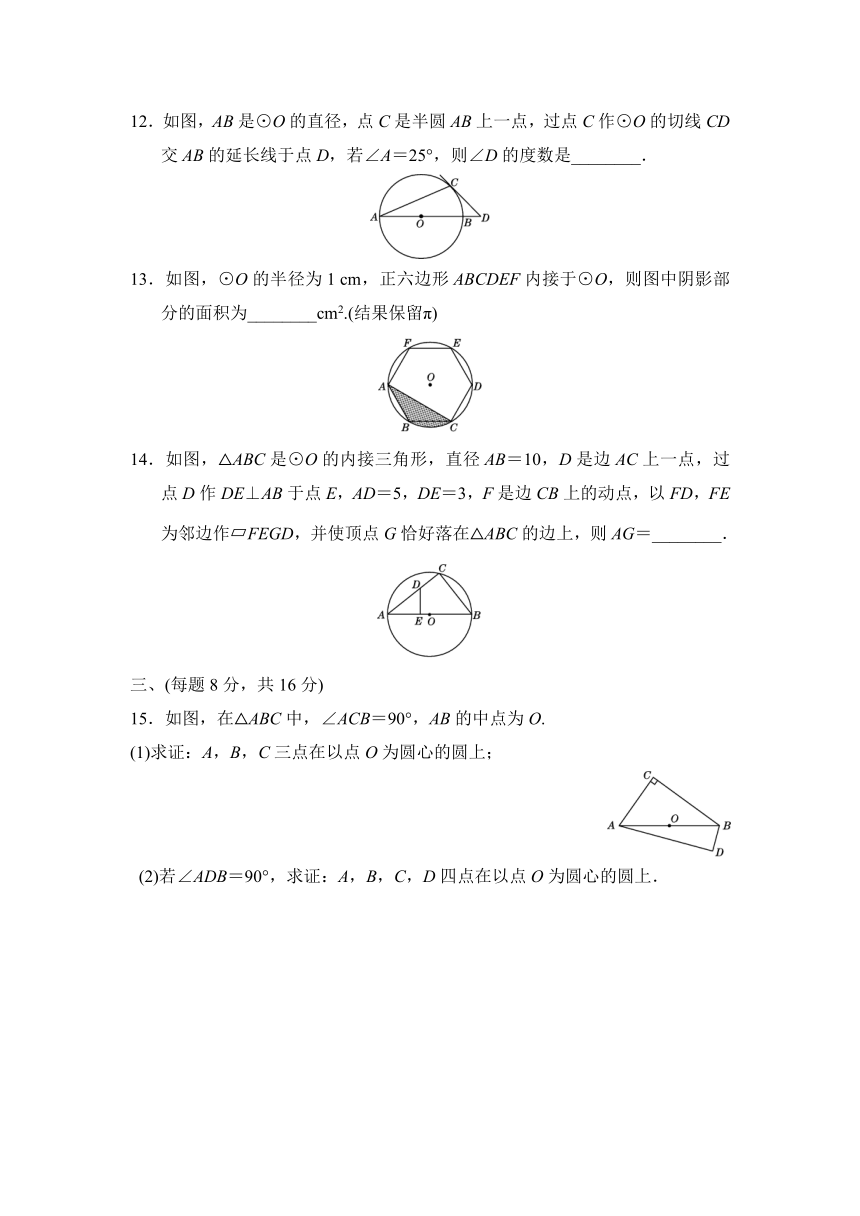
12.如图,AB是⊙O的直径,点C是半圆AB上一点,过点C作⊙O的切线CD交AB的延长线于点D,若∠A=25°,则∠D的度数是________.
13.如图,⊙O的半径为1
cm,正六边形ABCDEF内接于⊙O,则图中阴影部分的面积为________cm2.(结果保留π)
14.如图,△ABC是⊙O的内接三角形,直径AB=10,D是边AC上一点,过点D作DE⊥AB于点E,AD=5,DE=3,F是边CB上的动点,以FD,FE为邻边作 FEGD,并使顶点G恰好落在△ABC的边上,则AG=________.
三、(每题8分,共16分)
15.如图,在△ABC中,∠ACB=90°,AB的中点为O.
(1)求证:A,B,C三点在以点O为圆心的圆上;
(2)若∠ADB=90°,求证:A,B,C,D四点在以点O为圆心的圆上.
16.如图,在平面直角坐标系中,△ABC的三个顶点的坐标分别为A(1,-4),B(3,-3),C(1,-1).每个小方格都是边长为1个单位长度的正方形.
(1)将△ABC沿y轴向上平移5个单位长度,画出平移后得到的△A1B1C1;
(2)将△ABC绕点O按顺时针方向旋转90°,画出旋转后得到的△A2B2C2,并求出点A旋转到点A2所经过的路径长.
四、(每题8分,共16分)
17.如图,在△ABC中,AB=6,AC=3,BC边上的高AD=2,⊙O经过A,B,C三点,求⊙O的直径AE的长.
18.已知在△ABC中,AB=BC,以AB为直径的⊙O分别交AC,BC于点D,E,连接ED.
(1)求证:ED=DC;
(2)若CD=6,EC=4
,求AB的长.
五、(每题10分,共20分)
19.如图,⊙C经过坐标原点O,且与两坐标轴分别交于点A(0,4)与点B,M是⊙C上一点,且∠BMO=120°.
(1)求C点坐标;
(2)若把⊙C平移到与两坐标轴都相切,直接写出平移后的C点坐标.
20.如图,有一座圆弧形拱桥,它的跨度AB=60
m,拱高PM=18
m,当洪水泛滥到跨度只有30
m时,就要开始泄洪.若拱顶离水面只有4
m,即PN=4
m,请通过计算说明需不需要泄洪.
六、(12分)
21.如图,AB是⊙O的直径,CD是⊙O的一条弦,且CD⊥AB于点E.
(1)求证:∠BCO=∠D;
(2)若CD=4
,AE=2,求⊙O的半径.
七、(12分)
22.如图,△ABC内接于⊙O,D是⊙O的直径AB的延长线上一点,∠DCB=∠OAC.过圆心O作BC的平行线交DC的延长线于点E.
(1)求证:CD是⊙O的切线;
(2)若CD=4,CE=6,求⊙O的半径及tan∠OCB的值.
八、(14分)
23.如图,在平面直角坐标系xOy中,M是x轴正半轴上一点,⊙M与x轴的正半轴交于A,B两点,A在B的左侧,且OA,OB的长是方程x2-12x+27=0的两根,ON是⊙M的切线,N为切点,N在第四象限.
(1)求⊙M的直径;
(2)求直线ON的表达式;
(3)在x轴上是否存在一点T,使△OTN是等腰三角形?若存在,请求出所有符合条件的点T的坐标;若不存在,请说明理由.
答案
一、1.B 2.A 3.A
4.A 点拨:∵∠AOB=70°,
∴∠C=∠D=∠AOB=35°,
∴∠C+∠D=70°.
5.C 6.C
7.A 点拨:如图,连接PC,PA,过点P作PD⊥AB于点D,
∵⊙P与y轴相切于点C(0,3),
∴PC⊥y轴,∴四边形PDOC是矩形,∴PD=OC=3,
∵A(1,0),B(9,0),∴AB=9-1=8,
∴AD=AB=×8=4,∴OD=AD+OA=4+1=5,∴P(5,3),
∵直线y=kx-3恰好平分⊙P的面积,∴直线y=kx-3必过P点,
∴3=5k-3,解得k=.故选A.
8.A
9.A 点拨:如图,∵⊙O截△ABC的三条边所得的弦长相等,
∴O到△ABC三条边的距离相等,即O是△ABC的内心,
∴∠1=∠2,∠3=∠4,
∴∠1+∠3=(180°-∠A)=×(180°-70°)=55°,
∴∠BOC=180°-(∠1+∠3)=180°-55°=125°.
10.D
二、11.50°
12.
40° 点拨:连接OC,
∵OA=OC,
∴∠A=∠OCA=25°.
∴∠DOC=∠A+∠OCA=50°.
∵CD是⊙O的切线,
∴∠OCD=90°.
∴∠D=180°-90°-50°=40°.
13.
14.或
三、15.证明:(1)连接OC.
∵∠ACB=90°,AB的中点为O,
∴OA=OC=OB.
∴A,B,C三点在以点O为圆心的圆上.
(2)连接OD.
∵AB的中点为O,
∴在Rt△ABC和Rt△ABD中,有OA=OB=OC=OD.
∴A,B,C,D四点在以点O为圆心的圆上.
16.解:(1)如图,△A1B1C1即为所求.
(2)如图,△A2B2C2即为所求.连接OA.
由勾股定理得,OA==,点A旋转到点A2所经过的路径长为=.
四、17.解:连接CE,sin
B===.易知∠E=∠B,∠ACE=90°,
∴sin
E=sin
B===.
∴AE=9.
18.(1)证明:∵A,B,E,D四点共圆,
∴∠DEC=∠A,
∵AB=BC,
∴∠A=∠C,
∴∠DEC=∠C,
∴ED=DC.
(2)解:连接BD,
∵AB为⊙O的直径,∴∠ADB=90°,即BD⊥AC,
∵AB=BC,CD=6,∴AD=DC=6,∴AC=12,
∵∠A=∠DEC,∠C=∠C,∴△DEC∽△BAC,
∴=,∴=,解得BC=6
,
∵AB=BC,∴AB=6
.
五、19.解:(1)连接AB,由⊙C经过坐标原点O,∠AOB=90°,易知AB过点C.过点C作CD⊥OB于点D.
∴OD=OB,CD=OA.
∵点A的坐标为(0,4),∴OA=4.∴CD=2.
∵∠BMO=120°,∴∠BAO=60°.
在Rt△ABO中,OB=OA·tan
∠BAO=4
.
∴OD=2
.∴点C的坐标为(-2
,2).
(2)平移后的C点坐标为(4,4)或(-4,4)或(-4,-4)或(4,-4).
20.解:设圆弧所在圆的圆心为O,半径为R
m.连接OM,OA,OA′,如图.易知点O在PM的延长线上,且OP⊥AB,OP⊥A′B′.
∵AB=60
m,∴AM=30
m.
∵PM=18
m,∴OM=(R-18)m.
在Rt△AOM中,由勾股定理得R2=(R-18)2+302,解得R=34.
在Rt△A′NO中,由勾股定理得OA′2=A′N2+(OP-PN)2,
解得A′N=16
m(负值舍去).
∴A′B′=32
m>30
m.
∴不需要泄洪.
六、21.(1)证明:∵OC=OB,
∴∠BCO=∠B.
又∵∠B=∠D,∴∠BCO=∠D.
(2)解:∵AB是⊙O的直径,且CD⊥AB于点E,
∴CE=CD=×4
=2
.
在Rt△OCE中,OC2=CE2+OE2,
设⊙O的半径为r,则OC=r,OE=OA-AE=r-2,
∴r2=(2
)2+(r-2)2,解得r=3,∴⊙O的半径为3.
七、22.(1)证明:∵OA=OC,∴∠OAC=∠OCA,
∵∠DCB=∠OAC,∴∠OCA=∠DCB,
∵AB是⊙O的直径,∴∠ACB=90°,
∴∠OCA+∠OCB=90°,∴∠DCB+∠OCB=90°,
即∠OCD=90°,∴OC⊥DC,∴CD是⊙O的切线.
(2)解:∵OE∥BC,∴=,
∵CD=4,CE=6,∴==.
设BD=2x,则OB=3x,
∴OD=OB+BD=5x.
在Rt△OCD中,OC2+CD2=OD2,
∴(3x)2+42=(5x)2,解得x=1(负值已舍去),
∴OC=3x=3,即⊙O的半径为3,
∵BC∥OE,∴∠OCB=∠EOC.
在Rt△OCE中,tan∠EOC===2.
∴tan∠OCB=2.
八、23.解:(1)解方程x2-12x+27=0,得x1=3,x2=9.
∵A在B的左侧,∴点A坐标为(3,0),
点B坐标为(9,0).∴OA=3,OB=9.
∴AB=OB-OA=6,即⊙M的直径为6.
(2)作NC⊥OM于C,连接MN.
∵OM=OA+AM=3+AB=6,MN=3,∴MN=OM.
∵ON是⊙M的切线,∴MN⊥ON.
∴∠MON=30°,易得N,
设直线ON的表达式为y=kx,将N点坐标代入,得k=-
,
解得k=-.
∴直线ON的表达式为y=-x.
(3)存在.以点O为圆心,ON长为半径画弧,交x轴于两点T1,T2,
∴T1(-3
,0),T2(3
,0);以点N为圆心,ON长为半径画弧,交x轴于点T3,原点O,∴T3(9,0);
作ON的垂直平分线,交x轴于T4,设OT4=m,则CT4=-m,
在Rt△CNT4中,利用勾股定理求得m=3,∴T4(3,0).
一、选择题(每题4分,共40分)
1.在下列四个图案中,不是中心对称图形的是( )
2.已知⊙O的半径为6,点P在⊙O内,则OP的长可能是( )
A.5
B.6
C.7
D.8
3.已知⊙O的直径为12
cm,圆心到直线l的距离为5
cm,则直线l与⊙O的公共点的个数为( )
A.2
B.1
C.0
D.无法确定
4.如图,在⊙O中,∠AOB=70°,点C,D是⊙O上任意两点,则∠C+∠D的度数是( )
A.70°
B.80°
C.90°
D.140°
5.如图,在⊙O中,弦AB的长为6
cm,圆心O到AB的距离为4
cm,则⊙O的半径长为( )
A.3
cm
B.4
cm
C.5
cm
D.6
cm
6.如图,⊙O是△ABC的内切圆,切点分别是D,E,F,已知∠A=100°,∠C=30°,则∠DFE的度数是( )
A.55°
B.60°
C.65°
D.70°
7.如图,⊙P与y轴相切于点C(0,3),与x轴相交于点A(1,0),B(9,0).直线y=kx-3恰好平分⊙P的面积,那么k的值是( )
A.
B.
C.
D.2
8.如图是一张圆形纸片,小华利用它的阴影部分来制作一个圆锥的侧面,则这个圆锥的底面圆的半径是( )
A.3.6
B.1.6
C.3
D.6
9.如图,⊙O截△ABC的三条边所得的弦长相等,若∠A=70°,则∠BOC的度数为( )
A.125°
B.120°
C.130°
D.115°
10.如图,已知⊙O的直径CD为2,的度数为80°,点B是的中点,点P在直径CD上移动,则BP+AP的最小值为( )
A.1
B.2
C.2
D.
二、填空题(每题5分,共20分)
11.如图,A,B,C,D四点在⊙O上,∠B=130°,则∠ADC的度数是________.
12.如图,AB是⊙O的直径,点C是半圆AB上一点,过点C作⊙O的切线CD交AB的延长线于点D,若∠A=25°,则∠D的度数是________.
13.如图,⊙O的半径为1
cm,正六边形ABCDEF内接于⊙O,则图中阴影部分的面积为________cm2.(结果保留π)
14.如图,△ABC是⊙O的内接三角形,直径AB=10,D是边AC上一点,过点D作DE⊥AB于点E,AD=5,DE=3,F是边CB上的动点,以FD,FE为邻边作 FEGD,并使顶点G恰好落在△ABC的边上,则AG=________.
三、(每题8分,共16分)
15.如图,在△ABC中,∠ACB=90°,AB的中点为O.
(1)求证:A,B,C三点在以点O为圆心的圆上;
(2)若∠ADB=90°,求证:A,B,C,D四点在以点O为圆心的圆上.
16.如图,在平面直角坐标系中,△ABC的三个顶点的坐标分别为A(1,-4),B(3,-3),C(1,-1).每个小方格都是边长为1个单位长度的正方形.
(1)将△ABC沿y轴向上平移5个单位长度,画出平移后得到的△A1B1C1;
(2)将△ABC绕点O按顺时针方向旋转90°,画出旋转后得到的△A2B2C2,并求出点A旋转到点A2所经过的路径长.
四、(每题8分,共16分)
17.如图,在△ABC中,AB=6,AC=3,BC边上的高AD=2,⊙O经过A,B,C三点,求⊙O的直径AE的长.
18.已知在△ABC中,AB=BC,以AB为直径的⊙O分别交AC,BC于点D,E,连接ED.
(1)求证:ED=DC;
(2)若CD=6,EC=4
,求AB的长.
五、(每题10分,共20分)
19.如图,⊙C经过坐标原点O,且与两坐标轴分别交于点A(0,4)与点B,M是⊙C上一点,且∠BMO=120°.
(1)求C点坐标;
(2)若把⊙C平移到与两坐标轴都相切,直接写出平移后的C点坐标.
20.如图,有一座圆弧形拱桥,它的跨度AB=60
m,拱高PM=18
m,当洪水泛滥到跨度只有30
m时,就要开始泄洪.若拱顶离水面只有4
m,即PN=4
m,请通过计算说明需不需要泄洪.
六、(12分)
21.如图,AB是⊙O的直径,CD是⊙O的一条弦,且CD⊥AB于点E.
(1)求证:∠BCO=∠D;
(2)若CD=4
,AE=2,求⊙O的半径.
七、(12分)
22.如图,△ABC内接于⊙O,D是⊙O的直径AB的延长线上一点,∠DCB=∠OAC.过圆心O作BC的平行线交DC的延长线于点E.
(1)求证:CD是⊙O的切线;
(2)若CD=4,CE=6,求⊙O的半径及tan∠OCB的值.
八、(14分)
23.如图,在平面直角坐标系xOy中,M是x轴正半轴上一点,⊙M与x轴的正半轴交于A,B两点,A在B的左侧,且OA,OB的长是方程x2-12x+27=0的两根,ON是⊙M的切线,N为切点,N在第四象限.
(1)求⊙M的直径;
(2)求直线ON的表达式;
(3)在x轴上是否存在一点T,使△OTN是等腰三角形?若存在,请求出所有符合条件的点T的坐标;若不存在,请说明理由.
答案
一、1.B 2.A 3.A
4.A 点拨:∵∠AOB=70°,
∴∠C=∠D=∠AOB=35°,
∴∠C+∠D=70°.
5.C 6.C
7.A 点拨:如图,连接PC,PA,过点P作PD⊥AB于点D,
∵⊙P与y轴相切于点C(0,3),
∴PC⊥y轴,∴四边形PDOC是矩形,∴PD=OC=3,
∵A(1,0),B(9,0),∴AB=9-1=8,
∴AD=AB=×8=4,∴OD=AD+OA=4+1=5,∴P(5,3),
∵直线y=kx-3恰好平分⊙P的面积,∴直线y=kx-3必过P点,
∴3=5k-3,解得k=.故选A.
8.A
9.A 点拨:如图,∵⊙O截△ABC的三条边所得的弦长相等,
∴O到△ABC三条边的距离相等,即O是△ABC的内心,
∴∠1=∠2,∠3=∠4,
∴∠1+∠3=(180°-∠A)=×(180°-70°)=55°,
∴∠BOC=180°-(∠1+∠3)=180°-55°=125°.
10.D
二、11.50°
12.
40° 点拨:连接OC,
∵OA=OC,
∴∠A=∠OCA=25°.
∴∠DOC=∠A+∠OCA=50°.
∵CD是⊙O的切线,
∴∠OCD=90°.
∴∠D=180°-90°-50°=40°.
13.
14.或
三、15.证明:(1)连接OC.
∵∠ACB=90°,AB的中点为O,
∴OA=OC=OB.
∴A,B,C三点在以点O为圆心的圆上.
(2)连接OD.
∵AB的中点为O,
∴在Rt△ABC和Rt△ABD中,有OA=OB=OC=OD.
∴A,B,C,D四点在以点O为圆心的圆上.
16.解:(1)如图,△A1B1C1即为所求.
(2)如图,△A2B2C2即为所求.连接OA.
由勾股定理得,OA==,点A旋转到点A2所经过的路径长为=.
四、17.解:连接CE,sin
B===.易知∠E=∠B,∠ACE=90°,
∴sin
E=sin
B===.
∴AE=9.
18.(1)证明:∵A,B,E,D四点共圆,
∴∠DEC=∠A,
∵AB=BC,
∴∠A=∠C,
∴∠DEC=∠C,
∴ED=DC.
(2)解:连接BD,
∵AB为⊙O的直径,∴∠ADB=90°,即BD⊥AC,
∵AB=BC,CD=6,∴AD=DC=6,∴AC=12,
∵∠A=∠DEC,∠C=∠C,∴△DEC∽△BAC,
∴=,∴=,解得BC=6
,
∵AB=BC,∴AB=6
.
五、19.解:(1)连接AB,由⊙C经过坐标原点O,∠AOB=90°,易知AB过点C.过点C作CD⊥OB于点D.
∴OD=OB,CD=OA.
∵点A的坐标为(0,4),∴OA=4.∴CD=2.
∵∠BMO=120°,∴∠BAO=60°.
在Rt△ABO中,OB=OA·tan
∠BAO=4
.
∴OD=2
.∴点C的坐标为(-2
,2).
(2)平移后的C点坐标为(4,4)或(-4,4)或(-4,-4)或(4,-4).
20.解:设圆弧所在圆的圆心为O,半径为R
m.连接OM,OA,OA′,如图.易知点O在PM的延长线上,且OP⊥AB,OP⊥A′B′.
∵AB=60
m,∴AM=30
m.
∵PM=18
m,∴OM=(R-18)m.
在Rt△AOM中,由勾股定理得R2=(R-18)2+302,解得R=34.
在Rt△A′NO中,由勾股定理得OA′2=A′N2+(OP-PN)2,
解得A′N=16
m(负值舍去).
∴A′B′=32
m>30
m.
∴不需要泄洪.
六、21.(1)证明:∵OC=OB,
∴∠BCO=∠B.
又∵∠B=∠D,∴∠BCO=∠D.
(2)解:∵AB是⊙O的直径,且CD⊥AB于点E,
∴CE=CD=×4
=2
.
在Rt△OCE中,OC2=CE2+OE2,
设⊙O的半径为r,则OC=r,OE=OA-AE=r-2,
∴r2=(2
)2+(r-2)2,解得r=3,∴⊙O的半径为3.
七、22.(1)证明:∵OA=OC,∴∠OAC=∠OCA,
∵∠DCB=∠OAC,∴∠OCA=∠DCB,
∵AB是⊙O的直径,∴∠ACB=90°,
∴∠OCA+∠OCB=90°,∴∠DCB+∠OCB=90°,
即∠OCD=90°,∴OC⊥DC,∴CD是⊙O的切线.
(2)解:∵OE∥BC,∴=,
∵CD=4,CE=6,∴==.
设BD=2x,则OB=3x,
∴OD=OB+BD=5x.
在Rt△OCD中,OC2+CD2=OD2,
∴(3x)2+42=(5x)2,解得x=1(负值已舍去),
∴OC=3x=3,即⊙O的半径为3,
∵BC∥OE,∴∠OCB=∠EOC.
在Rt△OCE中,tan∠EOC===2.
∴tan∠OCB=2.
八、23.解:(1)解方程x2-12x+27=0,得x1=3,x2=9.
∵A在B的左侧,∴点A坐标为(3,0),
点B坐标为(9,0).∴OA=3,OB=9.
∴AB=OB-OA=6,即⊙M的直径为6.
(2)作NC⊥OM于C,连接MN.
∵OM=OA+AM=3+AB=6,MN=3,∴MN=OM.
∵ON是⊙M的切线,∴MN⊥ON.
∴∠MON=30°,易得N,
设直线ON的表达式为y=kx,将N点坐标代入,得k=-
,
解得k=-.
∴直线ON的表达式为y=-x.
(3)存在.以点O为圆心,ON长为半径画弧,交x轴于两点T1,T2,
∴T1(-3
,0),T2(3
,0);以点N为圆心,ON长为半径画弧,交x轴于点T3,原点O,∴T3(9,0);
作ON的垂直平分线,交x轴于T4,设OT4=m,则CT4=-m,
在Rt△CNT4中,利用勾股定理求得m=3,∴T4(3,0).
同课章节目录
