2021-2022学年苏科版九年级数学上册2.3 确定圆的条件课件(23张)
文档属性
| 名称 | 2021-2022学年苏科版九年级数学上册2.3 确定圆的条件课件(23张) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-04 00:00:00 | ||
图片预览




文档简介
(共23张PPT)
2.3
确定圆的条件
2002年1月,江苏省考古队在江阴云亭镇花山东侧的佘城遗址,发现了一座商周古城,其建筑和使用年代距今约3500-3100年之间。
情景创设
考古队在佘城遗址挖掘时,发现一圆形碎片,你能帮助这位考古队画出这个碎片所在的整圆,以便于进行深入的研究吗?
情境创设:
1、过一点可以作几条直线?
2、过几点可确定一条直线?
两点确定一条直线!
知识回顾
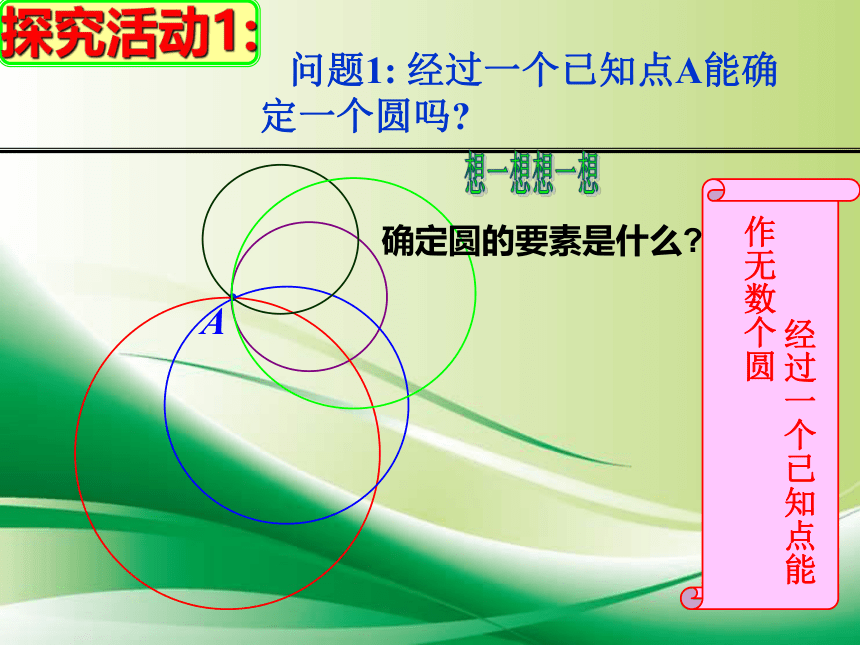
问题1:
经过一个已知点A能确定一个圆吗
A
经过一个已知点能作无数个圆
确定圆的要素是什么
探究活动1:
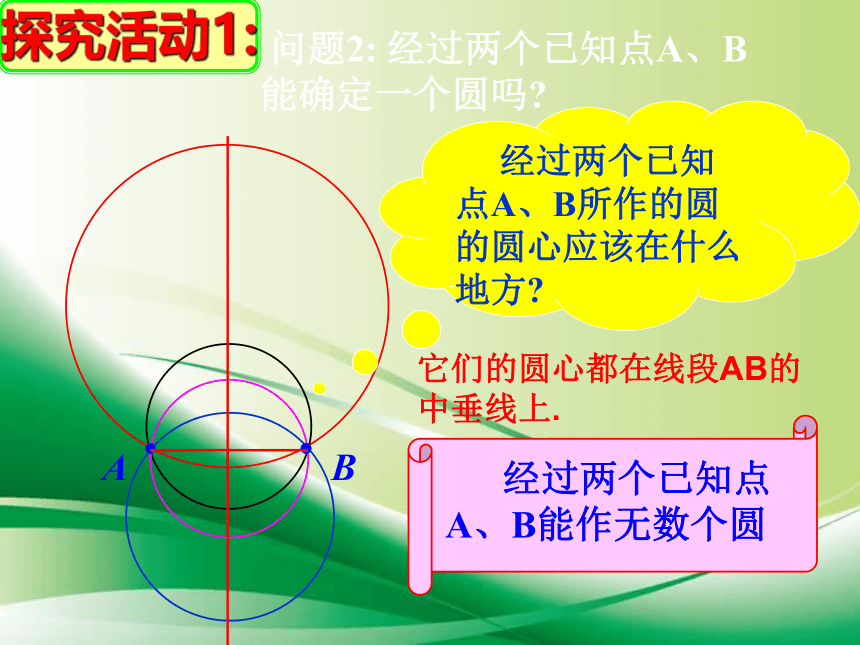
问题2:
经过两个已知点A、B能确定一个圆吗
A
B
经过两个已知点A、B能作无数个圆
经过两个已知点A、B所作的圆的圆心应该在什么地方
它们的圆心都在线段AB的中垂线上.
探究活动1:
A
B
C
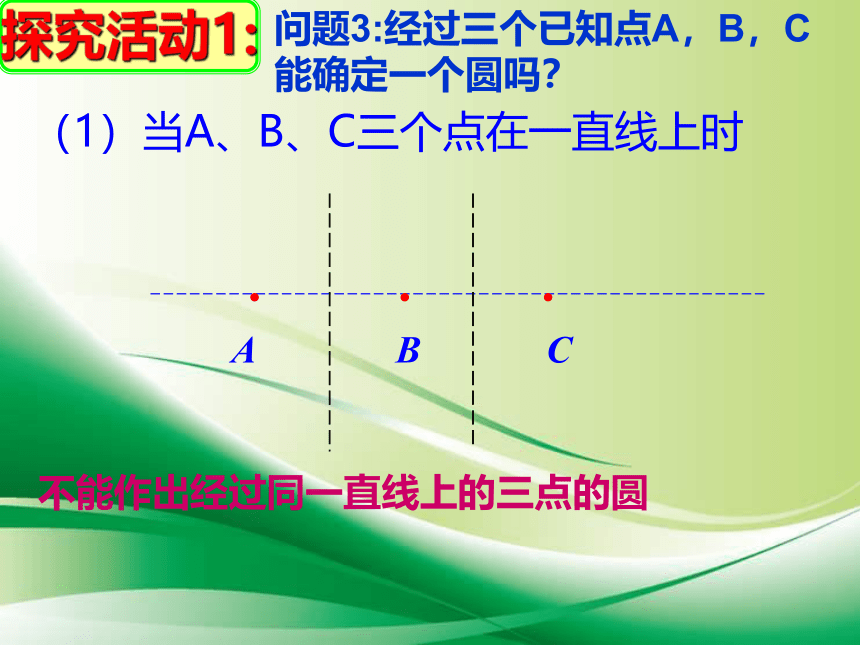
(1)当A、B、C三个点在一直线上时
探究活动1:
问题3:经过三个已知点A,B,C能确定一个圆吗?
不能作出经过同一直线上的三点的圆
O
A
B
C
探究活动1:
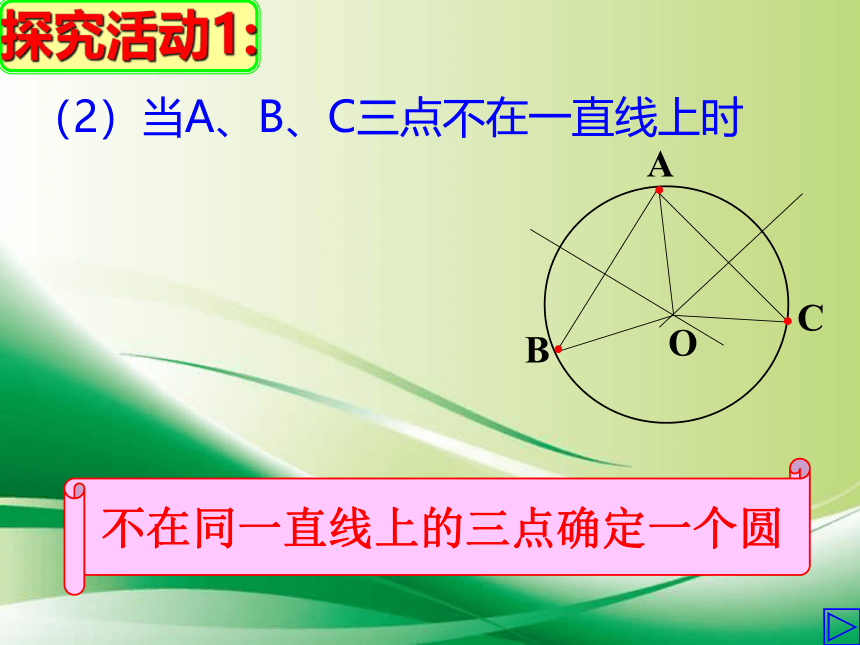
(2)当A、B、C三点不在一直线上时
不在同一直线上的三点确定一个圆
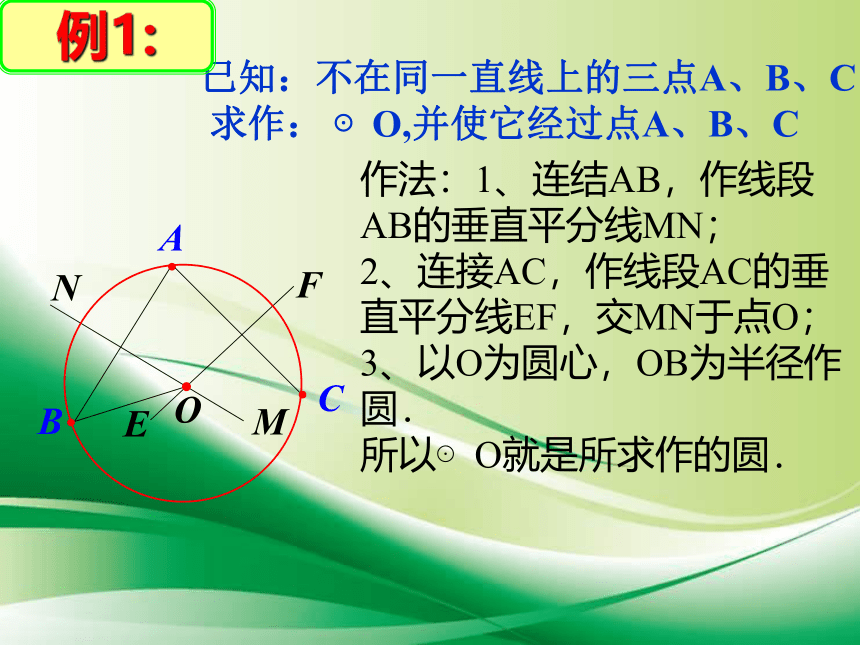
已知:不在同一直线上的三点A、B、C
求作:
⊙O,并使它经过点A、B、C
作法:1、连结AB,作线段AB的垂直平分线MN;
2、连接AC,作线段AC的垂直平分线EF,交MN于点O;
3、以O为圆心,OB为半径作圆.
所以⊙O就是所求作的圆.
O
N
M
F
E
A
B
C
例1:
方法:
1、在圆弧上任取三点A、B、C。
2、作线段AB、BC的垂直平分线,其交点O即为圆心。
3、以点O为圆心,OC长为半径作圆。
⊙O即为所求。
A
B
C
O
探究应用1:
现在你能帮助考古队完成圆形碎片的复原工作了吗?
经过三角形各个顶点的圆
叫做三角形的外接圆,三角形外接圆的圆心叫做三角形的外心,这个三角形叫做圆的内接三角形。
如图:⊙O是△ABC的外接圆,点O是△ABC的外心
,△ABC是⊙O的内接三角形,
外心是△ABC三条边的垂直平分线的交点,它到三角形的三个顶点的距离相等。
C
A
B
O
感受新知:
画出过以下三角形各顶点的圆
A
B
C
●O
A
B
C
C
A
B
┐
●O
●O
1、比较这三个三角形外心的位置,你有何发现?
(图一)
(图二)
(图三)
2、图二中,若AB=3,BC=4,则它的外接圆半径是多少?
探究活动2:
1、判断:
(1)经过三点一定可以作圆。(
)
(2)三角形的外心就是这个三角形两边垂直平分线的交点。(
)
(3)任意一个三角形一定有一个外接圆,并且只有一个外接圆;(
)
(4)任意一个圆一定有一个内接三角形,并且只有一个内接三角形;(
)
(5)等腰三角形的外心一定在这个三角形内。(
)
课堂反馈:
(1)、
下列命题不正确的是(
)
A.过一点有无数个圆.
B.过两点有无数个圆.
C.弦是圆的一部分.
D.过同一直线上三点不能画圆.
(2)、三角形的外心具有的性质是(
)
A.到三边的距离相等.
B.到三个顶点的距离相等.
C.外心在三角形的外部.
D.外心在三角形的内部
课堂反馈:
2
、选择:
3、Rt△ABC中,有两条边的长分别为6和8,则这个直角三角形的外接圆半径长为___
.
课堂反馈:
4、如图,在正方形网格中建立直角坐标系,
一条圆弧经过网格点A、B、C,设此弧
所在圆的圆心为O点,则点O坐标为:____
o
5、某一个城市在一块空地新建了三个居民小区,它们分别为A、B、C,其中B、A所在直线和A、C所在直线垂直,B、A之间距离500米,A、C之间距离1200米.现要想规划一所中学,使这所中学到三个小区的距离相等.请问同学们这所中学建在哪个位置?你怎么快速地在图上确定这个位置呢?你知道这个距离是多少吗?
●
●
●
B
A
C
课堂反馈:
挑战自我:
亲爱的同学们:通过今天对确定圆的条件的探索,相信你一定颇有收获,那就让我们来挑战自我吧!
你能联系实际生活,设计出一个与这节课所学内容相关的数学问题吗?
知识应用:
1、小明不慎把家中的圆形玻璃打碎了,其中的四片碎片如图所示,为配到与原来一样大小的圆形玻璃,小明只需要带到商店去的玻璃片应该是(
)
A、①
B、②
C、③
D、④
2、针对云亭的旅游开发,项目开发部决定修建一条圆形的小火车观光线路,要求这条线路经过如图这四个景区,你有办法实现这个规划吗?
知识应用:
通过本课的学习,你有什么收获?
回顾总结
2.3
确定圆的条件
2002年1月,江苏省考古队在江阴云亭镇花山东侧的佘城遗址,发现了一座商周古城,其建筑和使用年代距今约3500-3100年之间。
情景创设
考古队在佘城遗址挖掘时,发现一圆形碎片,你能帮助这位考古队画出这个碎片所在的整圆,以便于进行深入的研究吗?
情境创设:
1、过一点可以作几条直线?
2、过几点可确定一条直线?
两点确定一条直线!
知识回顾
问题1:
经过一个已知点A能确定一个圆吗
A
经过一个已知点能作无数个圆
确定圆的要素是什么
探究活动1:
问题2:
经过两个已知点A、B能确定一个圆吗
A
B
经过两个已知点A、B能作无数个圆
经过两个已知点A、B所作的圆的圆心应该在什么地方
它们的圆心都在线段AB的中垂线上.
探究活动1:
A
B
C
(1)当A、B、C三个点在一直线上时
探究活动1:
问题3:经过三个已知点A,B,C能确定一个圆吗?
不能作出经过同一直线上的三点的圆
O
A
B
C
探究活动1:
(2)当A、B、C三点不在一直线上时
不在同一直线上的三点确定一个圆
已知:不在同一直线上的三点A、B、C
求作:
⊙O,并使它经过点A、B、C
作法:1、连结AB,作线段AB的垂直平分线MN;
2、连接AC,作线段AC的垂直平分线EF,交MN于点O;
3、以O为圆心,OB为半径作圆.
所以⊙O就是所求作的圆.
O
N
M
F
E
A
B
C
例1:
方法:
1、在圆弧上任取三点A、B、C。
2、作线段AB、BC的垂直平分线,其交点O即为圆心。
3、以点O为圆心,OC长为半径作圆。
⊙O即为所求。
A
B
C
O
探究应用1:
现在你能帮助考古队完成圆形碎片的复原工作了吗?
经过三角形各个顶点的圆
叫做三角形的外接圆,三角形外接圆的圆心叫做三角形的外心,这个三角形叫做圆的内接三角形。
如图:⊙O是△ABC的外接圆,点O是△ABC的外心
,△ABC是⊙O的内接三角形,
外心是△ABC三条边的垂直平分线的交点,它到三角形的三个顶点的距离相等。
C
A
B
O
感受新知:
画出过以下三角形各顶点的圆
A
B
C
●O
A
B
C
C
A
B
┐
●O
●O
1、比较这三个三角形外心的位置,你有何发现?
(图一)
(图二)
(图三)
2、图二中,若AB=3,BC=4,则它的外接圆半径是多少?
探究活动2:
1、判断:
(1)经过三点一定可以作圆。(
)
(2)三角形的外心就是这个三角形两边垂直平分线的交点。(
)
(3)任意一个三角形一定有一个外接圆,并且只有一个外接圆;(
)
(4)任意一个圆一定有一个内接三角形,并且只有一个内接三角形;(
)
(5)等腰三角形的外心一定在这个三角形内。(
)
课堂反馈:
(1)、
下列命题不正确的是(
)
A.过一点有无数个圆.
B.过两点有无数个圆.
C.弦是圆的一部分.
D.过同一直线上三点不能画圆.
(2)、三角形的外心具有的性质是(
)
A.到三边的距离相等.
B.到三个顶点的距离相等.
C.外心在三角形的外部.
D.外心在三角形的内部
课堂反馈:
2
、选择:
3、Rt△ABC中,有两条边的长分别为6和8,则这个直角三角形的外接圆半径长为___
.
课堂反馈:
4、如图,在正方形网格中建立直角坐标系,
一条圆弧经过网格点A、B、C,设此弧
所在圆的圆心为O点,则点O坐标为:____
o
5、某一个城市在一块空地新建了三个居民小区,它们分别为A、B、C,其中B、A所在直线和A、C所在直线垂直,B、A之间距离500米,A、C之间距离1200米.现要想规划一所中学,使这所中学到三个小区的距离相等.请问同学们这所中学建在哪个位置?你怎么快速地在图上确定这个位置呢?你知道这个距离是多少吗?
●
●
●
B
A
C
课堂反馈:
挑战自我:
亲爱的同学们:通过今天对确定圆的条件的探索,相信你一定颇有收获,那就让我们来挑战自我吧!
你能联系实际生活,设计出一个与这节课所学内容相关的数学问题吗?
知识应用:
1、小明不慎把家中的圆形玻璃打碎了,其中的四片碎片如图所示,为配到与原来一样大小的圆形玻璃,小明只需要带到商店去的玻璃片应该是(
)
A、①
B、②
C、③
D、④
2、针对云亭的旅游开发,项目开发部决定修建一条圆形的小火车观光线路,要求这条线路经过如图这四个景区,你有办法实现这个规划吗?
知识应用:
通过本课的学习,你有什么收获?
回顾总结
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
