2021-2022学年苏科版七年级数学上册3.1 字母表示数课件(23张)
文档属性
| 名称 | 2021-2022学年苏科版七年级数学上册3.1 字母表示数课件(23张) |  | |
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-04 15:46:39 | ||
图片预览






文档简介
(共23张PPT)
3.1 字母表示数
初中数学七年级
上册
(苏科版)
在生活中我们经常用图标表示某种意义.
走进生活:
失物招领启示
小明今天上午在校园内捡到一个钱包,钱包内有人民币n元,请失主到教导处认领.
××年×月×日
走进生活:
1.观察下列等式:
2+5
=
5+2;
3+(-2)=(-2)+3;
0+(-4)=(-4)+0;
……
由以上各式,联想到什么运算律?如何表示?
走近生活:
在数学中,经常需要用字母来表示数.
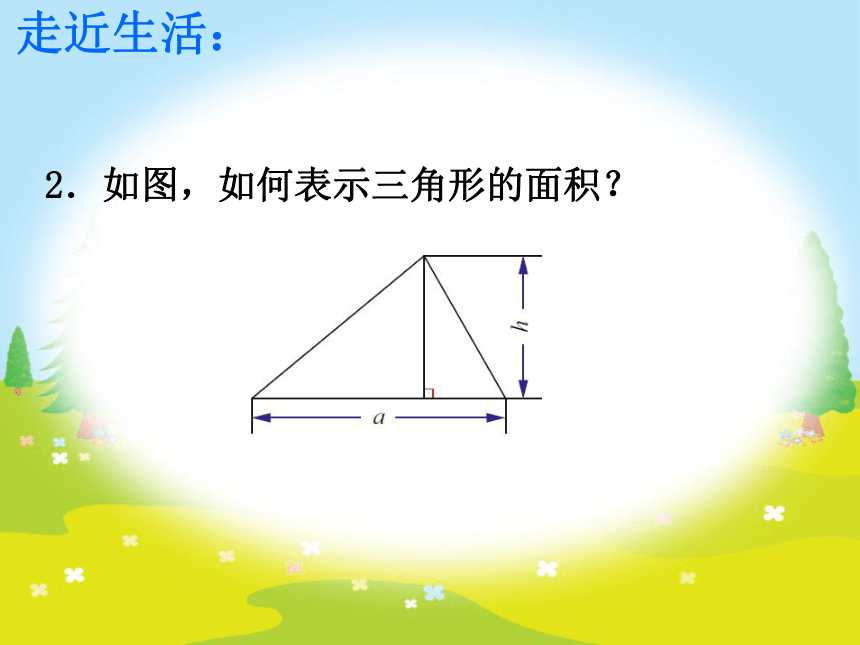
2.如图,如何表示三角形的面积?
走近生活:
数学实验室一:
第(1)个图形中有1个小正方形.
第(2)个图形比第(1)个图形多_____个小正方形.
第(3)个图形比第(2)个图形多_____个小正方形.
第(4)个图形比第(3)个图形多_____个小正方形.
3
5
7
1.
第(10)个图形比第(9)个图形多几个小正方形?
3.
第(n)个比第(n-1)个呢?
你还有什么发现?
2.
第(100)个比第(99)个呢?
数学实验室一:
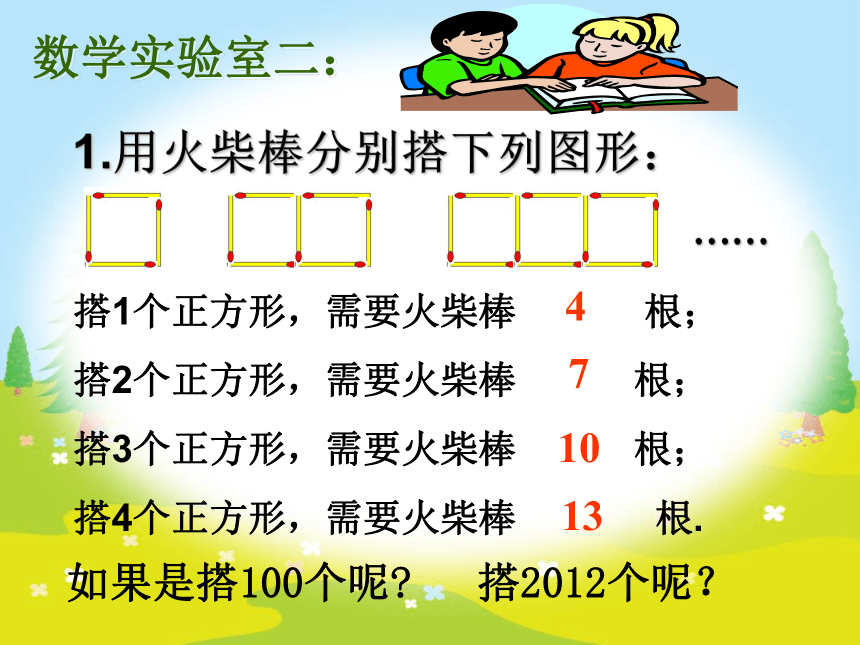
1.用火柴棒分别搭下列图形:
搭1个正方形,需要火柴棒
根;
搭2个正方形,需要火柴棒
根;
搭3个正方形,需要火柴棒
根;
搭4个正方形,需要火柴棒
根.
……
4
7
10
13
如果是搭100个呢
搭2012个呢?
数学实验室二:
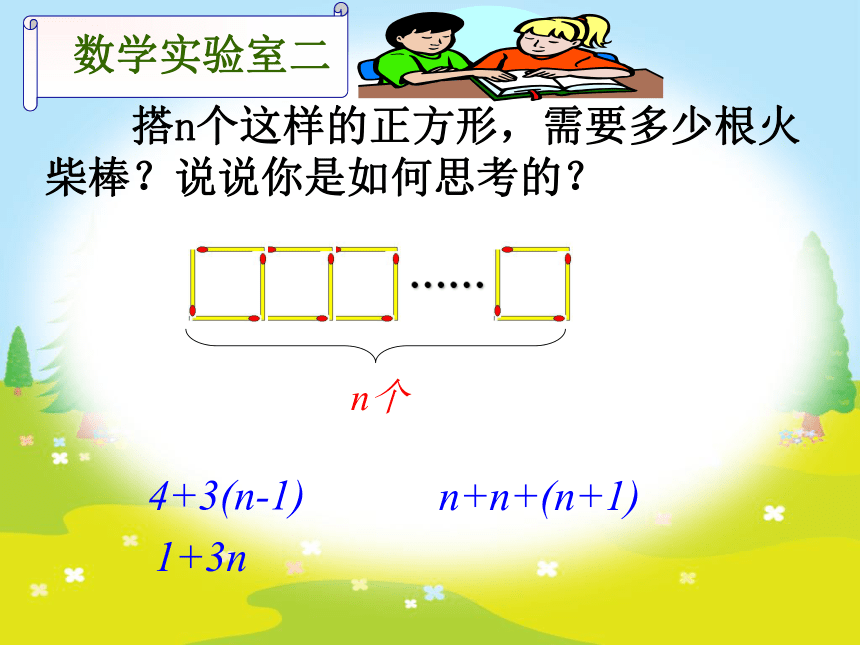
搭n个这样的正方形,需要多少根火柴棒?说说你是如何思考的?
……
n个
4+3(n-1)
n+n+(n+1)
1+3n
数学实验室二
4+3(n-1)
(n-1)个
……
数学实验室二
n+n+(n+1)
n根
n根
……
……
……
数学实验室二
1+3n
n个
……
数学实验室二
1、
观察月历的涂色框内的三个数之间有何关系?
2011年5月
日
一
二
三
四
五
六
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
a
a
-1
a+1
数学实验室三
2、
观察月历的涂色框内的三个数之间有何关系?
2011年5月
日
一
二
三
四
五
六
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
a
a
-7
a+7
数学实验室三
3、观察月历的涂色框内的四个数之间有何关系?
2011年5月
日
一
二
三
四
五
六
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
a
+1
a
a+7
a+8
数学实验室三
4、涂色框内的九个数之间又有什么关系呢?
2011年5月
日
一
二
三
四
五
六
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
数学实验室三
用字母表示数,可以使问题中的数量关系表示得更简明,更具有一般性。
例1
小亮跑步的速度是a米/秒,是小莉跑步
速度的3倍,请用代数式表示,小莉跑步的速度
是_______米/秒,两人的速度和是_______米/秒。
例题讲解:
注意
数和表示数的字母相乘,乘号可以省略不写,或用“●”来代替。数和字母相乘,在省略乘号时,要把数字写在字母的前面。除法结果用分数形式。
后接单位的相加式子要用括号括起来.
补充例题
例1、用字母表示数
(1)比a小1的数是
(2)比a大7的数是
(3)减去a的差是6的数是
例2、一个圆的直径是dcm,则这个圆的面积是
cm2
例3、我们知道:34=3×10+4
765=7×100+6×10+5=7×102+6×10+5
(1)类似的,5769=5×
+7×
+6×
+9
(2)若一个两位数,个位数字是a,十位数字是b,那么这个两位数为
(3)若一个三位数,各位数字是a,十位数字是b,百位数字是c,那么这个三位数为
。
试一试
1.小明今年n岁,小明比小丽大2岁,小丽今年_________岁.
2.小丽t
h走了s
km,她的平均速度是___________km/h.
3.一件羊毛衫标价a元,若按标价的8折出售,则这件羊毛衫的售价是__________元.
4.一个长方形的长是宽的2倍,如果宽为am
,那么这个长方形的面积是
m2
.
r
(n-2)
0.8a
2a2
5.一套校服,上衣a元,裤子比上衣便宜15元,裤子
元.
6.练习本每本m元,小丽买了5本,小亮买了2本,小丽比小亮多用
元.
7.学生剧场的楼上有a个座位,楼下有b个座位,楼上、楼下共有座位
个.
8.公共汽车上有40人,到达某站后,下车m人,上车n人,这时车上共有
人.
试一试
(a-15)
(5m-2m)
(a+b)
(40-m+n)
1.用字母表示数可以简明地描述许多实际问题中的数量关系.
小结:
2.尝试从具体问题情境中抽象出数量关系和变化规律.
作业:课本P68页习题1
.2.
3.1 字母表示数
初中数学七年级
上册
(苏科版)
在生活中我们经常用图标表示某种意义.
走进生活:
失物招领启示
小明今天上午在校园内捡到一个钱包,钱包内有人民币n元,请失主到教导处认领.
××年×月×日
走进生活:
1.观察下列等式:
2+5
=
5+2;
3+(-2)=(-2)+3;
0+(-4)=(-4)+0;
……
由以上各式,联想到什么运算律?如何表示?
走近生活:
在数学中,经常需要用字母来表示数.
2.如图,如何表示三角形的面积?
走近生活:
数学实验室一:
第(1)个图形中有1个小正方形.
第(2)个图形比第(1)个图形多_____个小正方形.
第(3)个图形比第(2)个图形多_____个小正方形.
第(4)个图形比第(3)个图形多_____个小正方形.
3
5
7
1.
第(10)个图形比第(9)个图形多几个小正方形?
3.
第(n)个比第(n-1)个呢?
你还有什么发现?
2.
第(100)个比第(99)个呢?
数学实验室一:
1.用火柴棒分别搭下列图形:
搭1个正方形,需要火柴棒
根;
搭2个正方形,需要火柴棒
根;
搭3个正方形,需要火柴棒
根;
搭4个正方形,需要火柴棒
根.
……
4
7
10
13
如果是搭100个呢
搭2012个呢?
数学实验室二:
搭n个这样的正方形,需要多少根火柴棒?说说你是如何思考的?
……
n个
4+3(n-1)
n+n+(n+1)
1+3n
数学实验室二
4+3(n-1)
(n-1)个
……
数学实验室二
n+n+(n+1)
n根
n根
……
……
……
数学实验室二
1+3n
n个
……
数学实验室二
1、
观察月历的涂色框内的三个数之间有何关系?
2011年5月
日
一
二
三
四
五
六
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
a
a
-1
a+1
数学实验室三
2、
观察月历的涂色框内的三个数之间有何关系?
2011年5月
日
一
二
三
四
五
六
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
a
a
-7
a+7
数学实验室三
3、观察月历的涂色框内的四个数之间有何关系?
2011年5月
日
一
二
三
四
五
六
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
a
+1
a
a+7
a+8
数学实验室三
4、涂色框内的九个数之间又有什么关系呢?
2011年5月
日
一
二
三
四
五
六
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
数学实验室三
用字母表示数,可以使问题中的数量关系表示得更简明,更具有一般性。
例1
小亮跑步的速度是a米/秒,是小莉跑步
速度的3倍,请用代数式表示,小莉跑步的速度
是_______米/秒,两人的速度和是_______米/秒。
例题讲解:
注意
数和表示数的字母相乘,乘号可以省略不写,或用“●”来代替。数和字母相乘,在省略乘号时,要把数字写在字母的前面。除法结果用分数形式。
后接单位的相加式子要用括号括起来.
补充例题
例1、用字母表示数
(1)比a小1的数是
(2)比a大7的数是
(3)减去a的差是6的数是
例2、一个圆的直径是dcm,则这个圆的面积是
cm2
例3、我们知道:34=3×10+4
765=7×100+6×10+5=7×102+6×10+5
(1)类似的,5769=5×
+7×
+6×
+9
(2)若一个两位数,个位数字是a,十位数字是b,那么这个两位数为
(3)若一个三位数,各位数字是a,十位数字是b,百位数字是c,那么这个三位数为
。
试一试
1.小明今年n岁,小明比小丽大2岁,小丽今年_________岁.
2.小丽t
h走了s
km,她的平均速度是___________km/h.
3.一件羊毛衫标价a元,若按标价的8折出售,则这件羊毛衫的售价是__________元.
4.一个长方形的长是宽的2倍,如果宽为am
,那么这个长方形的面积是
m2
.
r
(n-2)
0.8a
2a2
5.一套校服,上衣a元,裤子比上衣便宜15元,裤子
元.
6.练习本每本m元,小丽买了5本,小亮买了2本,小丽比小亮多用
元.
7.学生剧场的楼上有a个座位,楼下有b个座位,楼上、楼下共有座位
个.
8.公共汽车上有40人,到达某站后,下车m人,上车n人,这时车上共有
人.
试一试
(a-15)
(5m-2m)
(a+b)
(40-m+n)
1.用字母表示数可以简明地描述许多实际问题中的数量关系.
小结:
2.尝试从具体问题情境中抽象出数量关系和变化规律.
作业:课本P68页习题1
.2.
同课章节目录
- 第1章 我们与数学同行
- 1.1 生活 数学
- 1.2 活动 思考
- 第2章 有理数
- 2.1 正数与负数
- 2.2 有理数与无理数
- 2.3 数轴
- 2.4 绝对值与相反数
- 2.5 有理数的加法与减法
- 2.6 有理数的乘法与除法
- 2.7 有理数的乘方
- 2.8 有理数的混合运算
- 第3章 代数式
- 3.1 字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 3.4 合并同类项
- 3.5 去括号
- 3.6 整式的加减
- 第4章 一元一次方程
- 4.1 从问题到方程
- 4.2 解一元一次方程
- 4.3 用一元一次方程解决问题
- 第5章 走进图形世界
- 5.1 丰富的图形世界
- 5.2 图形的运动
- 5.3 展开与折叠
- 5.4 主视图、左视图、俯视图
- 第6章 平面图形的认识(一)
- 6.1 线段 射线 直线
- 6.2 角
- 6.3 余角 补角 对顶角
- 6.4 平行
- 6.5 垂直
