湘教版七上数学2.1用字母表示数 课件(共25张PPT)
文档属性
| 名称 | 湘教版七上数学2.1用字母表示数 课件(共25张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 3.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-07 20:55:06 | ||
图片预览








文档简介
(共25张PPT)
2.1
用字母表示数
湘教版
七年级上
教学目标
1.学会根据数量关系用字母表示数的方法;
2.能正确书写用字母表示出来的数;
3.从现实问题感知用字母表示数的意义;
4.体会抽象概括的数学思维方法,以及认识事物是从特殊到一般,再从一般到特殊的过程。
1.
在计算粮食产量时,总产量、亩产量、亩数三者之间
有什么关系?
2.
在车辆行驶、飞机飞行等问题中,路程、速度、时间
之间有什么关系?
新知导入
说一说:
总产量=亩产量×亩数
路程=速度×时间
在小学,我们根据数量关系,列出算式解答了很多实际问题。能不能用字母表示式子中的数呢?如果能,那么怎样用字母表示数呢?
新知导入
新知讲解
据中国新闻网2011年9月19日报道:中国工程院院士袁隆平指导的“Y两优2号”百亩①超级杂交稻试验田平均亩产926.6kg,创中国大面积水稻亩产的最高纪录.
新知讲解
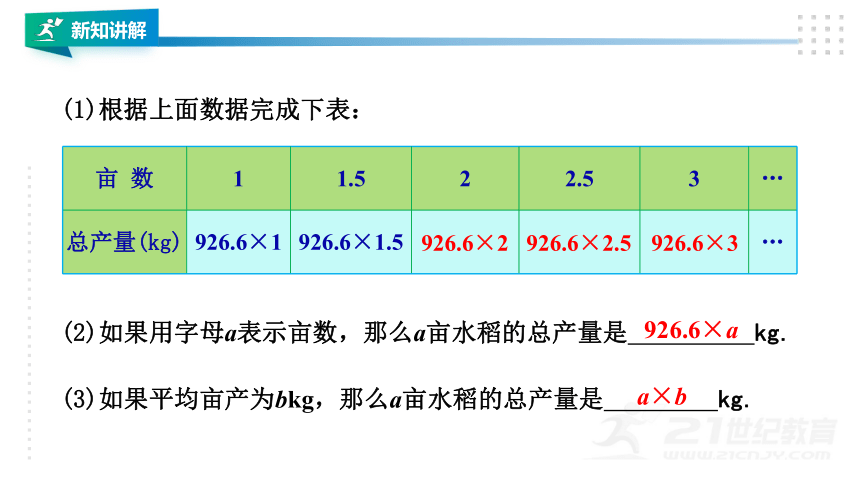
(2)如果用字母a表示亩数,那么a亩水稻的总产量是
kg.
亩
数
1
1.5
2
2.5
3
…
总产量(kg)
926.6×1
926.6×1.5
…
(3)如果平均亩产为bkg,那么a亩水稻的总产量是
kg.
(1)根据上面数据完成下表:
926.6×2
926.6×2.5
926.6×3
926.6×a
a×b
新知讲解
2011年9月29日21时16分,我国成功发射了“天宫一号”飞行器,它是目前中国最大、最重的在轨飞行航天器.已知“天宫一号”大约每小时绕地球飞行2.844
万千米,则它飞行2h,2.5h分别飞行了多少万千米?如果时间为th,那么它飞行了多少万千米?
新知讲解
“天宫一号”飞行2h飞行了
万千米,飞行2.5h飞行了
万千米.
“天宫一号”飞行
t
h飞行了
万千米.
2.844×2
2.844×2.5
2.844t
“天宫一号”每小时飞行2.844万千米,根据“路程=速度×时间”,可知:
新知讲解
从上面两个问题的解答,你发现了什么?
在实际问题的数量关系中,可以用字母表示数.
例题讲解
例1
填空:
(2)
a与b的2倍的积为
.
(1)
比a的0.6倍大c的数是
;
解:(1)a的0.6倍是0.6a,比a的0.6倍大c的数是0.6a+c;
(2)b的2倍是2b,a与b的2倍的积是a×2b,写成2ab.
例题讲解
例2
小莉以5km/h的速度,走了20km的路程,那么她走了多长时间?如用字母v表示速度,用字母s表示路程,那么她走的时间又如何表示呢?
解:小莉走20km所花的时间为:
分析:因为路程=速度×时间,所以时间=路程÷速度.
20÷5=4(h)
若用字母v表示速度,用字母s表示路程,则时间
例题讲解
从例1、例2可以看出,在用字母表示数时,有很多讲究,请你说一说:如何书写含有字母的式子?
说一说:
例题讲解
字母与字母相乘,“×”号通常省略不写或写成“·”,例如a×b可以写成ab或a·b;
数字与字母相乘,“×”号通常省略不写,例如926.6×a可以写成926.6a;
数字与数字相乘,仍用“×”号,也可以用“·”号,但要注意写在两数的中间位置,与小数点的位置不同;
例题讲解
在字母与数字的乘积中,数字通常写在字母的左边.
例如,a×2b=2ab.
字母除以字母,通常把除法写成类似于分数形式,
写成
.
例如:
巩固练习
1.
下列各式符合书写格式的是
(
)
A.
a×5
B.
x÷y
C.
6a+4b
D.
C
解析:A应写成5a,B应写成类似于分数的形式,D中带分数应写成假分数,因此A,B,D都不符合书写格式,C符合书写格式,故选C。
巩固练习
2.
用字母表示数
,得到的式子正确的是
(
)
A.
“负x的平方”记作-x
B.
“a的6倍与b的差”记作a×6-b
C.
“a与b的2倍的积”
记作2ab
D.
“9除以2x的商”记作9÷2x
C
解析:A应记作(-x) ,B应记作6a-b,D中带分数应记作类似于分数的形式,A,B,D都不符合书写格式,C符合书写格式,故选C。
巩固练习
3.
某建筑公司第1季度净收入a万元,第2季度净收入增长
15%,第2季度的净收入是(
)
A.
15%a万元
B.
(a+15%)万元
C.
a÷(1+15%)万元
D.
(1+15%)a万元
D
解析:把第1季度的净收入看作单位1,则第2季度的净收入是第1季度的(1+15%),用含字母a的式子表示就是(1+15%)a万元。故选D。
巩固练习
4.
比628的a倍多20的数是
。
628a+20
5.
甲数是x,比乙数的3倍多20,乙数是
。
6.
一个数的个位是3,十位是a,这个数是
。
7.
三个相邻的自然数,中间一个是n,右边一个是
.
10a+3
n+1
课堂总结
认真分析数量关系,把数量关系中的数量用字母表示;
注意书写要规范。
2.
如何规范书写含有字母的式子?
1.
用字母表示数要注意哪些问题?
字母与字母相乘,“×”号不写或写成“·”;
数与字母相乘,数在前面,“×”号不写或写成“·”;
数与数相乘,仍写“×”号或写成“·”;
字母与字母相除,写成类似于分数的形式。
作业布置
填空:
(1)小明上学骑自行车的速度是其步行速度的3倍,若小明的步行速度为am/s,则小明骑自行车的速度是
;
(2)学校有各种球共x个,其中蓝球占35%,则蓝球的个数
是
;
(3)比314的a倍多10的数是
;
(4)比15b的一半少3的数是
.
第57页课后练习:
3am/s
35%x
314a+10
作业布置
4.
填空:
(1)一个两位数,它的十位数字是a,个位数字是b,则这个两位数是
;
(2)利用乘法对加法的分配律可以得到3×5+6×5=
(3+6)
×5,如用a表示任意一个数,那么利用分配律可得3a+6b
=
.
习题2.1B组题:
10a+b
(3+6)a
作业布置
5.
已知x与y之间的关系如下表:
x
1
2
3
4
…
y
4+0.6
8+1.2
12+1.8
16+2.4
…
下面用x表示y的式子中,正确的是(
)
A.
y=4x+0.6
B.
y=(4+0.6)x
C.
y=4+0.6x
D.
y=4+0.6+x
C
作业布置
6.
某工厂的产量每年增长15%,如果第一年的产量是m,那么第二年、第三年的产量分别是多少
解:第二年的产量是(1
+
15%)m.
第三年的产量是(1
+
15%)m×(1
+
15%)=(1
+
15%) m.
https://www.21cnjy.com/help/help_extract.php
2.1
用字母表示数
湘教版
七年级上
教学目标
1.学会根据数量关系用字母表示数的方法;
2.能正确书写用字母表示出来的数;
3.从现实问题感知用字母表示数的意义;
4.体会抽象概括的数学思维方法,以及认识事物是从特殊到一般,再从一般到特殊的过程。
1.
在计算粮食产量时,总产量、亩产量、亩数三者之间
有什么关系?
2.
在车辆行驶、飞机飞行等问题中,路程、速度、时间
之间有什么关系?
新知导入
说一说:
总产量=亩产量×亩数
路程=速度×时间
在小学,我们根据数量关系,列出算式解答了很多实际问题。能不能用字母表示式子中的数呢?如果能,那么怎样用字母表示数呢?
新知导入
新知讲解
据中国新闻网2011年9月19日报道:中国工程院院士袁隆平指导的“Y两优2号”百亩①超级杂交稻试验田平均亩产926.6kg,创中国大面积水稻亩产的最高纪录.
新知讲解
(2)如果用字母a表示亩数,那么a亩水稻的总产量是
kg.
亩
数
1
1.5
2
2.5
3
…
总产量(kg)
926.6×1
926.6×1.5
…
(3)如果平均亩产为bkg,那么a亩水稻的总产量是
kg.
(1)根据上面数据完成下表:
926.6×2
926.6×2.5
926.6×3
926.6×a
a×b
新知讲解
2011年9月29日21时16分,我国成功发射了“天宫一号”飞行器,它是目前中国最大、最重的在轨飞行航天器.已知“天宫一号”大约每小时绕地球飞行2.844
万千米,则它飞行2h,2.5h分别飞行了多少万千米?如果时间为th,那么它飞行了多少万千米?
新知讲解
“天宫一号”飞行2h飞行了
万千米,飞行2.5h飞行了
万千米.
“天宫一号”飞行
t
h飞行了
万千米.
2.844×2
2.844×2.5
2.844t
“天宫一号”每小时飞行2.844万千米,根据“路程=速度×时间”,可知:
新知讲解
从上面两个问题的解答,你发现了什么?
在实际问题的数量关系中,可以用字母表示数.
例题讲解
例1
填空:
(2)
a与b的2倍的积为
.
(1)
比a的0.6倍大c的数是
;
解:(1)a的0.6倍是0.6a,比a的0.6倍大c的数是0.6a+c;
(2)b的2倍是2b,a与b的2倍的积是a×2b,写成2ab.
例题讲解
例2
小莉以5km/h的速度,走了20km的路程,那么她走了多长时间?如用字母v表示速度,用字母s表示路程,那么她走的时间又如何表示呢?
解:小莉走20km所花的时间为:
分析:因为路程=速度×时间,所以时间=路程÷速度.
20÷5=4(h)
若用字母v表示速度,用字母s表示路程,则时间
例题讲解
从例1、例2可以看出,在用字母表示数时,有很多讲究,请你说一说:如何书写含有字母的式子?
说一说:
例题讲解
字母与字母相乘,“×”号通常省略不写或写成“·”,例如a×b可以写成ab或a·b;
数字与字母相乘,“×”号通常省略不写,例如926.6×a可以写成926.6a;
数字与数字相乘,仍用“×”号,也可以用“·”号,但要注意写在两数的中间位置,与小数点的位置不同;
例题讲解
在字母与数字的乘积中,数字通常写在字母的左边.
例如,a×2b=2ab.
字母除以字母,通常把除法写成类似于分数形式,
写成
.
例如:
巩固练习
1.
下列各式符合书写格式的是
(
)
A.
a×5
B.
x÷y
C.
6a+4b
D.
C
解析:A应写成5a,B应写成类似于分数的形式,D中带分数应写成假分数,因此A,B,D都不符合书写格式,C符合书写格式,故选C。
巩固练习
2.
用字母表示数
,得到的式子正确的是
(
)
A.
“负x的平方”记作-x
B.
“a的6倍与b的差”记作a×6-b
C.
“a与b的2倍的积”
记作2ab
D.
“9除以2x的商”记作9÷2x
C
解析:A应记作(-x) ,B应记作6a-b,D中带分数应记作类似于分数的形式,A,B,D都不符合书写格式,C符合书写格式,故选C。
巩固练习
3.
某建筑公司第1季度净收入a万元,第2季度净收入增长
15%,第2季度的净收入是(
)
A.
15%a万元
B.
(a+15%)万元
C.
a÷(1+15%)万元
D.
(1+15%)a万元
D
解析:把第1季度的净收入看作单位1,则第2季度的净收入是第1季度的(1+15%),用含字母a的式子表示就是(1+15%)a万元。故选D。
巩固练习
4.
比628的a倍多20的数是
。
628a+20
5.
甲数是x,比乙数的3倍多20,乙数是
。
6.
一个数的个位是3,十位是a,这个数是
。
7.
三个相邻的自然数,中间一个是n,右边一个是
.
10a+3
n+1
课堂总结
认真分析数量关系,把数量关系中的数量用字母表示;
注意书写要规范。
2.
如何规范书写含有字母的式子?
1.
用字母表示数要注意哪些问题?
字母与字母相乘,“×”号不写或写成“·”;
数与字母相乘,数在前面,“×”号不写或写成“·”;
数与数相乘,仍写“×”号或写成“·”;
字母与字母相除,写成类似于分数的形式。
作业布置
填空:
(1)小明上学骑自行车的速度是其步行速度的3倍,若小明的步行速度为am/s,则小明骑自行车的速度是
;
(2)学校有各种球共x个,其中蓝球占35%,则蓝球的个数
是
;
(3)比314的a倍多10的数是
;
(4)比15b的一半少3的数是
.
第57页课后练习:
3am/s
35%x
314a+10
作业布置
4.
填空:
(1)一个两位数,它的十位数字是a,个位数字是b,则这个两位数是
;
(2)利用乘法对加法的分配律可以得到3×5+6×5=
(3+6)
×5,如用a表示任意一个数,那么利用分配律可得3a+6b
=
.
习题2.1B组题:
10a+b
(3+6)a
作业布置
5.
已知x与y之间的关系如下表:
x
1
2
3
4
…
y
4+0.6
8+1.2
12+1.8
16+2.4
…
下面用x表示y的式子中,正确的是(
)
A.
y=4x+0.6
B.
y=(4+0.6)x
C.
y=4+0.6x
D.
y=4+0.6+x
C
作业布置
6.
某工厂的产量每年增长15%,如果第一年的产量是m,那么第二年、第三年的产量分别是多少
解:第二年的产量是(1
+
15%)m.
第三年的产量是(1
+
15%)m×(1
+
15%)=(1
+
15%) m.
https://www.21cnjy.com/help/help_extract.php
同课章节目录
