湘教版七上数学2.5整式的加法和减法(第1课时) 课件(共25张PPT)
文档属性
| 名称 | 湘教版七上数学2.5整式的加法和减法(第1课时) 课件(共25张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 47.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-07 21:03:44 | ||
图片预览








文档简介
(共25张PPT)
2.5
整式的加法和减法(1)
湘教版
七年级上
教学目标
1.理解同类项的概念,能找出多项式中的同类项;
2.知道合并同类项的概念,学会合并同类项的方法;
3.了解两个多项式相等的概念;
4.经历探究合并同类项的过程,体会类比的价值;
5.经历合并同类项的过程,提高整式运算的能力;
1.
写出乘法分配律:a(b+c)
=
;
2.
3×4+5×4=(
)×4;
3.
2个a加上4个a等于
个a,2a+4a=
;
4.
8个ab减去3个ab等于
个ab,8ab-3ab=
.
新知导入
做一做:
6a
ab+ac
3+5
6
5
5ab
新知讲解
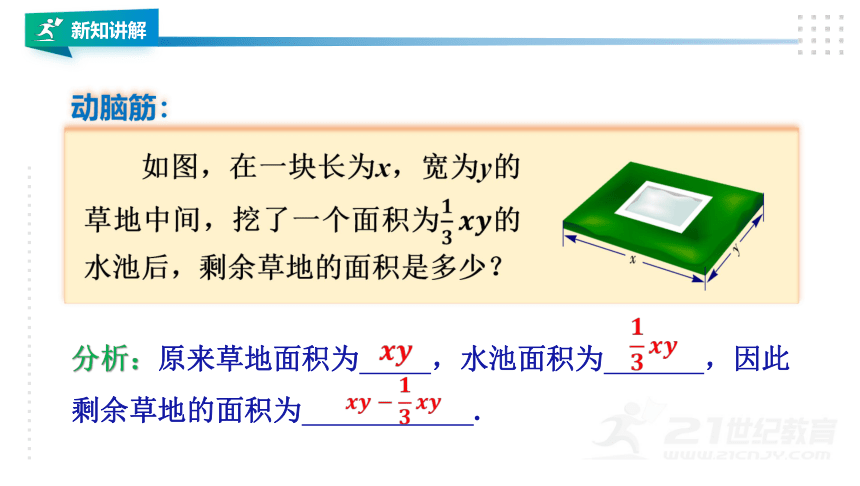
分析:原来草地面积为
,水池面积为
,因此
剩余草地的面积为
.
如图,在一块长为x,宽为y的草地中间,挖了一个面积为的水池后,剩余草地的面积是多少?
动脑筋:
例题讲解
多项式中的项和的字母及相同字母的指数有什么特点?
字母相同,并且相同字母的指数也相同
像多项式中的项,,它们含有的字母相同,并且相同字母的指数也分别相同,称它们为同类项
.
例如,在多项式x2y+3x+1-4x-5x2y
-5中,是同类项的有x2y与-5x2y,3x与-4x,1与-5.
新知讲解
多项式
x2y+3x+1-4x-5x2y-5中的同类项可以合并吗?
动脑筋:
我想可以,因为多项式中的字母表示的是数,所以我们可以运用交换律、结合律、分配律把多项式中的同类项进行合并.
新知讲解
x2y+3x+1-4x-5x2y-5
=
x2y-5x2y+3x-4x+1-5(交换律)
=
(x2y-5x2y)+(3x-4x)+(1-5)(结合律)
=
(1-5)x2y+(3-4)x+(-4)(分配律)
=
-4x2y-x-4.
新知讲解
例1
合并同类项:
(1);
(2).
例题讲解
解
(1)
利用分配律,把系数相加,字母及指数不变.
例题讲解
合并同类项时,只要把它们的系数相加,
字母和字母的指数不变.
例题讲解
从例题1我们可知:
例2
合并同类项:
(1);
(2).
例题讲解
解
找同类项.
交换律.
结合律.
(2).
例题讲解
解
找同类项.
交换律.
结合律.
像例2这样,先把同类项底下画不同的线标出,然后运用加法交换律和结合律,把同类项放在一起,最后把同类项的系数相加合并同类项.
例题讲解
你能归纳一下合并同类项的方法吗?
简单地说就是:
一找(标画同类项),二调(同类项调到一起),三合并。
熟练以后,可以不必把同类项调到一起而直接合并同类项.
例题讲解
这样合并同类项,只需两步即可完成,即:一找二并.
例2的第(2)题可以分两步这样做:
解
找同类项.
把系数相加.
多项式x -4x +7x -2x-5与多项式x +3x -6x+4x-5相等吗?
例题讲解
说一说:
两个式子合并同类项后都等于x +3x -2x-5.
两个多项式分别经过合并同类项后,如果它们的对应系数都相等,那么称这两个多项式相等.
因此,x -4x +7x -2x-5=x +3x -6x+4x-5.
巩固练习
1.
下列每组中的两个单项式是同类项的是
(
)
A.
4a与b
B.
-3xy 与5x y
C.
4ab与6ba
D.
与.
解析:字母相同,并且相同字母的指数也相同的项叫作同类项。C选项符合同类项的概念,故选C。
C
巩固练习
2.
多项式中,与是
同类项的项是
.
3.
已知与是同类项,则m=
。
2
巩固练习
4.
下列合并同类项,结果正确的是
(
)
A.
B.
=
C.
D.
D
课堂总结
字母相同,并且相同字母的指数也相同的项叫作同类项。
把多项式的项合并成一项,叫作合并同类项。
1.
什么叫做同类项?什么叫做合并同类项?
3.
两个多项式分别经过合并同类项后,如果它们的对应系数都相等,那么称这两个多项式相等.
2.
如何合并多项式的同类项?
先找出多项式的同类项,再把同类项的系数相加,字母连同指数不变。
作业布置
1.
请将下面的同类项用线连接起来:
第72页课后练习:
2x3
xy2
-5x
-7xy2
3x
-4x3
同类项的特征:
字母相同;
相同字母的指数相同;
所有常数项是同类项.
作业布置
2.
合并同类项:
+9;
;
.
作业布置
3.
下列两个多项式是否相等?
;
.
https://www.21cnjy.com/help/help_extract.php
2.5
整式的加法和减法(1)
湘教版
七年级上
教学目标
1.理解同类项的概念,能找出多项式中的同类项;
2.知道合并同类项的概念,学会合并同类项的方法;
3.了解两个多项式相等的概念;
4.经历探究合并同类项的过程,体会类比的价值;
5.经历合并同类项的过程,提高整式运算的能力;
1.
写出乘法分配律:a(b+c)
=
;
2.
3×4+5×4=(
)×4;
3.
2个a加上4个a等于
个a,2a+4a=
;
4.
8个ab减去3个ab等于
个ab,8ab-3ab=
.
新知导入
做一做:
6a
ab+ac
3+5
6
5
5ab
新知讲解
分析:原来草地面积为
,水池面积为
,因此
剩余草地的面积为
.
如图,在一块长为x,宽为y的草地中间,挖了一个面积为的水池后,剩余草地的面积是多少?
动脑筋:
例题讲解
多项式中的项和的字母及相同字母的指数有什么特点?
字母相同,并且相同字母的指数也相同
像多项式中的项,,它们含有的字母相同,并且相同字母的指数也分别相同,称它们为同类项
.
例如,在多项式x2y+3x+1-4x-5x2y
-5中,是同类项的有x2y与-5x2y,3x与-4x,1与-5.
新知讲解
多项式
x2y+3x+1-4x-5x2y-5中的同类项可以合并吗?
动脑筋:
我想可以,因为多项式中的字母表示的是数,所以我们可以运用交换律、结合律、分配律把多项式中的同类项进行合并.
新知讲解
x2y+3x+1-4x-5x2y-5
=
x2y-5x2y+3x-4x+1-5(交换律)
=
(x2y-5x2y)+(3x-4x)+(1-5)(结合律)
=
(1-5)x2y+(3-4)x+(-4)(分配律)
=
-4x2y-x-4.
新知讲解
例1
合并同类项:
(1);
(2).
例题讲解
解
(1)
利用分配律,把系数相加,字母及指数不变.
例题讲解
合并同类项时,只要把它们的系数相加,
字母和字母的指数不变.
例题讲解
从例题1我们可知:
例2
合并同类项:
(1);
(2).
例题讲解
解
找同类项.
交换律.
结合律.
(2).
例题讲解
解
找同类项.
交换律.
结合律.
像例2这样,先把同类项底下画不同的线标出,然后运用加法交换律和结合律,把同类项放在一起,最后把同类项的系数相加合并同类项.
例题讲解
你能归纳一下合并同类项的方法吗?
简单地说就是:
一找(标画同类项),二调(同类项调到一起),三合并。
熟练以后,可以不必把同类项调到一起而直接合并同类项.
例题讲解
这样合并同类项,只需两步即可完成,即:一找二并.
例2的第(2)题可以分两步这样做:
解
找同类项.
把系数相加.
多项式x -4x +7x -2x-5与多项式x +3x -6x+4x-5相等吗?
例题讲解
说一说:
两个式子合并同类项后都等于x +3x -2x-5.
两个多项式分别经过合并同类项后,如果它们的对应系数都相等,那么称这两个多项式相等.
因此,x -4x +7x -2x-5=x +3x -6x+4x-5.
巩固练习
1.
下列每组中的两个单项式是同类项的是
(
)
A.
4a与b
B.
-3xy 与5x y
C.
4ab与6ba
D.
与.
解析:字母相同,并且相同字母的指数也相同的项叫作同类项。C选项符合同类项的概念,故选C。
C
巩固练习
2.
多项式中,与是
同类项的项是
.
3.
已知与是同类项,则m=
。
2
巩固练习
4.
下列合并同类项,结果正确的是
(
)
A.
B.
=
C.
D.
D
课堂总结
字母相同,并且相同字母的指数也相同的项叫作同类项。
把多项式的项合并成一项,叫作合并同类项。
1.
什么叫做同类项?什么叫做合并同类项?
3.
两个多项式分别经过合并同类项后,如果它们的对应系数都相等,那么称这两个多项式相等.
2.
如何合并多项式的同类项?
先找出多项式的同类项,再把同类项的系数相加,字母连同指数不变。
作业布置
1.
请将下面的同类项用线连接起来:
第72页课后练习:
2x3
xy2
-5x
-7xy2
3x
-4x3
同类项的特征:
字母相同;
相同字母的指数相同;
所有常数项是同类项.
作业布置
2.
合并同类项:
+9;
;
.
作业布置
3.
下列两个多项式是否相等?
;
.
https://www.21cnjy.com/help/help_extract.php
同课章节目录
