3.2.1函数的单调性 课件(共22张PPT)
文档属性
| 名称 | 3.2.1函数的单调性 课件(共22张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-08 11:20:27 | ||
图片预览








文档简介
(共22张PPT)
3.2.1函数的单调性
人教A(2019)版
必修一
函数的基本表示法
解析法
列表法
图象法
分段函数
定义
图像
求函数解析式
待定系数法
配凑法
换元法
消元法
新知导入
在自变量的不同取值区
间,有不同对应关系的函数
叫做分段函数.
复习巩固
新知导入
画出下列函数图像并观察自变量与函数值的变化关系
y=2x+1(x
R
)
y=(x-1)2-1
(x
R
)
x
y
o
(1)
x
o
-1
2
(2)
(
)
y
1
1
o
x
y
(3)
随着自变量的增大函数值也在增大
随着自变量的增大函数值也在减小
在不同的区间上变化趋势不同
新知讲解
函数的单调性定义
一般地,设函数y=f(x)的定义域为I,区间D I.
如果对于区间D内的任意两个值x1,x2,当x1<x2时,都有f(x1)<f(x2),那么就说y=f(x)在区间D上是单调增函数,D称为y=f(x)的单调增区间.
如果对于区间D内的任意两个值x1,x2,当x1<x2时,都有f(x1)>f(x2),那么就说y=f(x)在区间D上是单调减函数,D称为y=f(x)的单调减区间.
如果函数y=f(x)在区间D上是单调增函数或单调减函数,那么就说函数y=f(x)在区间D上具有单调性.单调增区间和单调减区间统称为单调区间.
注意:定义中的x1,x2的任意性,即“任意取x1,x2”中“任意”二字绝不能去掉,
证明时
不能以特殊代替一般;
合作探究
y=2x+1(x
R
)
y=(x-1)2-1
(x
R
)
x
y
o
x
o
-1
2
(
)
y
1
1
o
x
y
(3)
(2)
(1)
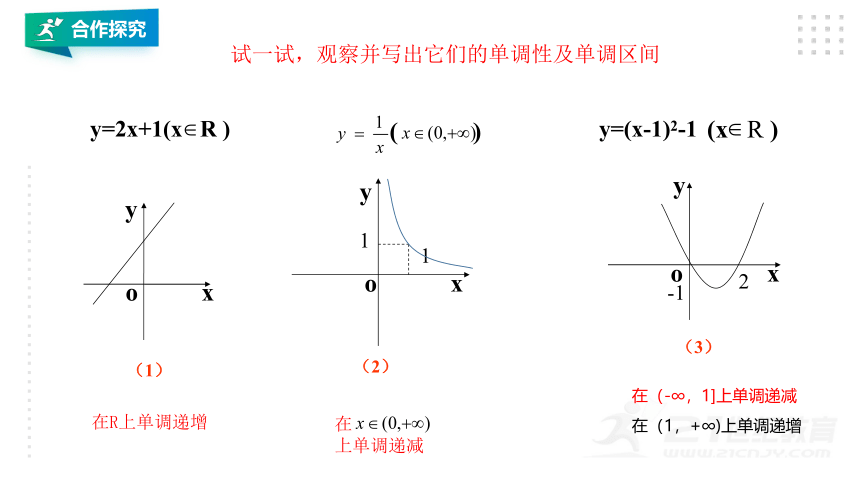
试一试,观察并写出它们的单调性及单调区间
在R上单调递增
在
上单调递减
在(-∞,1]上单调递减
在(1,+∞)上单调递增
合作探究
注意:一般地,在不连续的单调区间上,即使单调性相同也不
能取并集。
合作探究
合作探究
例1
根据定义,研究函数f(x)=kx+b(k≠0)的单调性.
解:函数f(x)=kx+b(k≠0)的定义域是R.?x1,x2∈R,且x1<x2,
则
f(x1)-f(x2)=(kx1+b)-(kx2+b)
=k(x1-x2)
由x1<x2,得x1-x2<0.所以
①当k>0时,k(x1-x2)<0.
于是
f(x1)-f(x2)<0,
即
f(x1)<f(x2).
这时,f(x)=kx+b是增函数
②当k<0时,k(x1-x2)>0.
于是
f(x1)-f(x2)>0,
即
f(x1)>f(x2).
这时,f(x)=kx+b是减函数.
一、利用定义判断证明函数的单调性
根据定义证明函数单调性的步骤:
⑴取值;⑵作差变形;⑶定号;⑷判断.
合作探究
例2
物理学中的玻意耳定律
(k为正常数)告诉我们,对于一定量的气体,当其体积V
减小时,压强P将增大.试对此用函数的单调性证明.
取值
作差变形
判断符号
合作探究
证明:
合作探究
试一试
合作探究
若函数f(x)=-x2-2(a+1)x+3在区间(-∞,3]上是增函数,求实数a的取值范围。
二、求参数取值范围
解一:(利用单调性定义)
任取
则
要使函数f(x)=-x2-2(a+1)x+3在区间(-∞,3]上是增函数,
则
即
因为
所以
所以
得
合作探究
解二:由二次函数图像和性质,
对称轴为x=-(a+1)
f(x)=-x2-2(a+1)x+3
-(a+1)
3
O
x
y
如图:由图像可知,
要使函数f(x)=-x2-2(a+1)x+3在区
间(-∞,3]上是增函数,则
合作探究
三、利用单调性解不等式
已知函数y=f(x)是(-∞,+∞)上的增函数,且f(2x-3)>f(5x-6),求实数x的取值范围.
合作探究
四、抽象函数单调性判断与证明
函数f(x)对任意的a、b∈R,都有f(a+b)=f(a)+f(b)-1,并且当x>0时,f(x)>1.
(1)求证:f(x)是R上的增函数;
(2)若f(4)=5,解不等式f(3m2-m-2)<3.
解 (1)证明:设x1,x2∈R,且x10,∴f(x2-x1)>1.
f(x2)-f(x1)=f[(x2-x1)+x1]-f(x1)
=f(x2-x1)+f(x1)-1-f(x1)=f(x2-x1)-1>0.
∴f(x2)>f(x1).
即f(x)是R上的增函数.
(2)∵f(4)=f(2+2)=f(2)+f(2)-1=5,
∴f(2)=3,
∴原不等式可化为f(3m2-m-2)∵f(x)是R上的增函数,
∴3m2-m-2<2,解得-1,
故m的解集为{m|-1}.
1.下列函数中,在区间(0,2)上为增函数的是
(
)
A.y=-x+1
B.y=
C.y=x2-4x+5
D.
解析
∵y=-x+1,y=x2-4x+5,
分别为一次函
数、
二次函数、反比例函数,从它们
的图象上可以看出在(0,2)上都是减函数.
C
2.已知函数y=f(x)是定义在R上的增函数,则f(x)=0的根
(
)
A.有且只有一个
B.有2个
C.至多有一个
D.以上均不对
B
解析
∵f(x)在R上是增函数,∴对任意x1,x2∈R,若x1反之亦成立.故
若存在f(x0)=0,则x0只有一个.
若对任意x∈R都无f(x)=0,则f(x)=0无根.
课堂练习
3.下列函数f(x)中,满足“对任意x1,x2∈(0,+∞),当x1f(x2)”的是(
)
A.
B.f(x)=(x-1)2
C.f(x)=ex
D.f(x)=ln(x+1)
A
课堂练习
4.写出y=|x2-2x-3|的单调区间.
所以y=|x2-2x-3|的单调减区间为(-∞,-1],[1,3];
单调增区间为[-1,1],[3,+∞).
5.已知函数f(x)=2x+1x+1.
判断函数在区间[1,+∞)上的单调性,并用定义证明你的结论;
解:f(x)在[1,+∞)上是增函数.证明如下:任取x1,x2∈[1,+∞),且x1f(x1)-f(x2)=
∵x1-x2<0,(x1+1)(x2+1)>0,所以f(x1)-f(x2)<0,f(x1)所以函数f(x)在[1,+∞)上是增函数.
课堂总结
1.单调性定义
注意x1,x2在其定义域内的任意性,杜绝以特殊代替任意.
3.函数的单调区间是指函数在定义域内的某个区间上单调递增或单调递减.
多个单调区间要分开写,即使在两个区间上的单调性相同,也不能用并集表示.
2.利用定义证明函数的单调性:一般步骤:取值、作差、变形、
确定符
号、得出结论.
板书设计
增函数
减函数
一般地,设函数f(x)的定义域为I.如果对于定义域I内某个区间D上的任意两个自变量x1,x2
当x1当x1(x2),那么就说函数f(x)在区间D上是减函数
自左向右看图象是上升的
自左向右看图象是下降的
定义
定义
图像
变化
趋势
作业布置
3.课本P86页,2、3、8
1.已知二次函数y=x2-2ax+1在区间(2,3)内是单调函数,求实数a
的取值范围.
2.作出函数f(x)=-x2+|x|的图像,并写出递减区间.
https://www.21cnjy.com/help/help_extract.php
3.2.1函数的单调性
人教A(2019)版
必修一
函数的基本表示法
解析法
列表法
图象法
分段函数
定义
图像
求函数解析式
待定系数法
配凑法
换元法
消元法
新知导入
在自变量的不同取值区
间,有不同对应关系的函数
叫做分段函数.
复习巩固
新知导入
画出下列函数图像并观察自变量与函数值的变化关系
y=2x+1(x
R
)
y=(x-1)2-1
(x
R
)
x
y
o
(1)
x
o
-1
2
(2)
(
)
y
1
1
o
x
y
(3)
随着自变量的增大函数值也在增大
随着自变量的增大函数值也在减小
在不同的区间上变化趋势不同
新知讲解
函数的单调性定义
一般地,设函数y=f(x)的定义域为I,区间D I.
如果对于区间D内的任意两个值x1,x2,当x1<x2时,都有f(x1)<f(x2),那么就说y=f(x)在区间D上是单调增函数,D称为y=f(x)的单调增区间.
如果对于区间D内的任意两个值x1,x2,当x1<x2时,都有f(x1)>f(x2),那么就说y=f(x)在区间D上是单调减函数,D称为y=f(x)的单调减区间.
如果函数y=f(x)在区间D上是单调增函数或单调减函数,那么就说函数y=f(x)在区间D上具有单调性.单调增区间和单调减区间统称为单调区间.
注意:定义中的x1,x2的任意性,即“任意取x1,x2”中“任意”二字绝不能去掉,
证明时
不能以特殊代替一般;
合作探究
y=2x+1(x
R
)
y=(x-1)2-1
(x
R
)
x
y
o
x
o
-1
2
(
)
y
1
1
o
x
y
(3)
(2)
(1)
试一试,观察并写出它们的单调性及单调区间
在R上单调递增
在
上单调递减
在(-∞,1]上单调递减
在(1,+∞)上单调递增
合作探究
注意:一般地,在不连续的单调区间上,即使单调性相同也不
能取并集。
合作探究
合作探究
例1
根据定义,研究函数f(x)=kx+b(k≠0)的单调性.
解:函数f(x)=kx+b(k≠0)的定义域是R.?x1,x2∈R,且x1<x2,
则
f(x1)-f(x2)=(kx1+b)-(kx2+b)
=k(x1-x2)
由x1<x2,得x1-x2<0.所以
①当k>0时,k(x1-x2)<0.
于是
f(x1)-f(x2)<0,
即
f(x1)<f(x2).
这时,f(x)=kx+b是增函数
②当k<0时,k(x1-x2)>0.
于是
f(x1)-f(x2)>0,
即
f(x1)>f(x2).
这时,f(x)=kx+b是减函数.
一、利用定义判断证明函数的单调性
根据定义证明函数单调性的步骤:
⑴取值;⑵作差变形;⑶定号;⑷判断.
合作探究
例2
物理学中的玻意耳定律
(k为正常数)告诉我们,对于一定量的气体,当其体积V
减小时,压强P将增大.试对此用函数的单调性证明.
取值
作差变形
判断符号
合作探究
证明:
合作探究
试一试
合作探究
若函数f(x)=-x2-2(a+1)x+3在区间(-∞,3]上是增函数,求实数a的取值范围。
二、求参数取值范围
解一:(利用单调性定义)
任取
则
要使函数f(x)=-x2-2(a+1)x+3在区间(-∞,3]上是增函数,
则
即
因为
所以
所以
得
合作探究
解二:由二次函数图像和性质,
对称轴为x=-(a+1)
f(x)=-x2-2(a+1)x+3
-(a+1)
3
O
x
y
如图:由图像可知,
要使函数f(x)=-x2-2(a+1)x+3在区
间(-∞,3]上是增函数,则
合作探究
三、利用单调性解不等式
已知函数y=f(x)是(-∞,+∞)上的增函数,且f(2x-3)>f(5x-6),求实数x的取值范围.
合作探究
四、抽象函数单调性判断与证明
函数f(x)对任意的a、b∈R,都有f(a+b)=f(a)+f(b)-1,并且当x>0时,f(x)>1.
(1)求证:f(x)是R上的增函数;
(2)若f(4)=5,解不等式f(3m2-m-2)<3.
解 (1)证明:设x1,x2∈R,且x1
f(x2)-f(x1)=f[(x2-x1)+x1]-f(x1)
=f(x2-x1)+f(x1)-1-f(x1)=f(x2-x1)-1>0.
∴f(x2)>f(x1).
即f(x)是R上的增函数.
(2)∵f(4)=f(2+2)=f(2)+f(2)-1=5,
∴f(2)=3,
∴原不等式可化为f(3m2-m-2)
∴3m2-m-2<2,解得-1
故m的解集为{m|-1
1.下列函数中,在区间(0,2)上为增函数的是
(
)
A.y=-x+1
B.y=
C.y=x2-4x+5
D.
解析
∵y=-x+1,y=x2-4x+5,
分别为一次函
数、
二次函数、反比例函数,从它们
的图象上可以看出在(0,2)上都是减函数.
C
2.已知函数y=f(x)是定义在R上的增函数,则f(x)=0的根
(
)
A.有且只有一个
B.有2个
C.至多有一个
D.以上均不对
B
解析
∵f(x)在R上是增函数,∴对任意x1,x2∈R,若x1
若存在f(x0)=0,则x0只有一个.
若对任意x∈R都无f(x)=0,则f(x)=0无根.
课堂练习
3.下列函数f(x)中,满足“对任意x1,x2∈(0,+∞),当x1
)
A.
B.f(x)=(x-1)2
C.f(x)=ex
D.f(x)=ln(x+1)
A
课堂练习
4.写出y=|x2-2x-3|的单调区间.
所以y=|x2-2x-3|的单调减区间为(-∞,-1],[1,3];
单调增区间为[-1,1],[3,+∞).
5.已知函数f(x)=2x+1x+1.
判断函数在区间[1,+∞)上的单调性,并用定义证明你的结论;
解:f(x)在[1,+∞)上是增函数.证明如下:任取x1,x2∈[1,+∞),且x1
∵x1-x2<0,(x1+1)(x2+1)>0,所以f(x1)-f(x2)<0,f(x1)
课堂总结
1.单调性定义
注意x1,x2在其定义域内的任意性,杜绝以特殊代替任意.
3.函数的单调区间是指函数在定义域内的某个区间上单调递增或单调递减.
多个单调区间要分开写,即使在两个区间上的单调性相同,也不能用并集表示.
2.利用定义证明函数的单调性:一般步骤:取值、作差、变形、
确定符
号、得出结论.
板书设计
增函数
减函数
一般地,设函数f(x)的定义域为I.如果对于定义域I内某个区间D上的任意两个自变量x1,x2
当x1
自左向右看图象是上升的
自左向右看图象是下降的
定义
定义
图像
变化
趋势
作业布置
3.课本P86页,2、3、8
1.已知二次函数y=x2-2ax+1在区间(2,3)内是单调函数,求实数a
的取值范围.
2.作出函数f(x)=-x2+|x|的图像,并写出递减区间.
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
