17.3勾股定理-同步练习-2021-2022学年冀教版八年级数学上册(word版含答案)
文档属性
| 名称 | 17.3勾股定理-同步练习-2021-2022学年冀教版八年级数学上册(word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 344.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-05 07:34:50 | ||
图片预览


文档简介
2021-2022学年八年级数学上册(冀教版)
17.3勾股定理(3)-同步练习
时间:60分钟
一、单选题
1.若三角形的三边长分别为,,,且满足,则此三角形中最大的角是(
)
A.锐角
B.直角
C.钝角
D.无法确定
2.已知,,是三角形的三边长,且,那么此三角形是(
)
A.以为斜边的直角三角形
B.以为斜边的直角三角形
C.等腰直角三角形
D.锐角三角形
3.中,,,BC边上的中线,则AC的长是(
).
A.6
B.8
C.10
D.16
4.如图:在一个边长为1的小正方形组成的方格稿纸上,有A、B、C、D、E、F、G七个点,则在下列任选三个点的方案中可以构成直角三角形的是( )
A.点A、点B、点C
B.点A、点D、点G
C.点B、点E、点F
D.点B、点G、点E
5.下列长度的各组线段能组成一个直角三角形的是(
)
A.
B.
C.
D.
6.如图,牧童家在B处,A、B两处相距河岸的距离AC、BD分别为500m和300m,且C、D两处的距离为600m,天黑牧童从A处将牛牵到河边去饮水,在赶回家,那么牧童最少要走(
)
A.800m
B.1000m
C.1200m
D.1500m
7.如图1,园丁住宅小区有一块草坪如图所示.已知AB=3米,BC=4米,CD=12米,DA=13米,且AB⊥BC,这块草坪的面积是(
)
A.24米2
B.36米2
C.48米2
D.72米2
8.在平面直角坐标系中,点A的坐标为(1,1),点B的坐标为(11,1),点C到直线AB的距离为5,且△ABC是直角三角形,则满足条件的C点有( )
A.4个
B.5个
C.6个
D.8个
二、填空题
9.一个三角形的三边长a,b,c满足,则这个三角形最长边上的高为________.
10.将△ABC放在每个小正方形的边长为1的网格中,点A、B、C均落在格点上,ABC的面积等于________;
11.在△中,若三边长分别为9、12、15,则以两个这样的三角形拼成的长方形的面积为______.
12.如图,在东西走向的铁路上有A、B两站(视为直线上的两点)相距36千米,在A、B的正北分别有C、D两个蔬菜基地,其中C到A站的距离为24千米,D到B站的距离为12千米,现要在铁路AB上建一个蔬菜加工厂E,使蔬菜基地C、D到E的距离相等,则E站应建在距A站_____千米的地方.
13.如图,一辆小汽车在一条城市街路上直道行驶,某一时刻刚好行驶到路对面车速检测仪A处的正前方30m的C处,过了2s后,测得小汽车与车速检测仪间的距离为50m,则这辆小汽车的速度是__m/s.
14.在高5cm,长13cm的一段台阶上铺上地毯,台阶的剖面如图所示,地毯的长度至少需要______m.
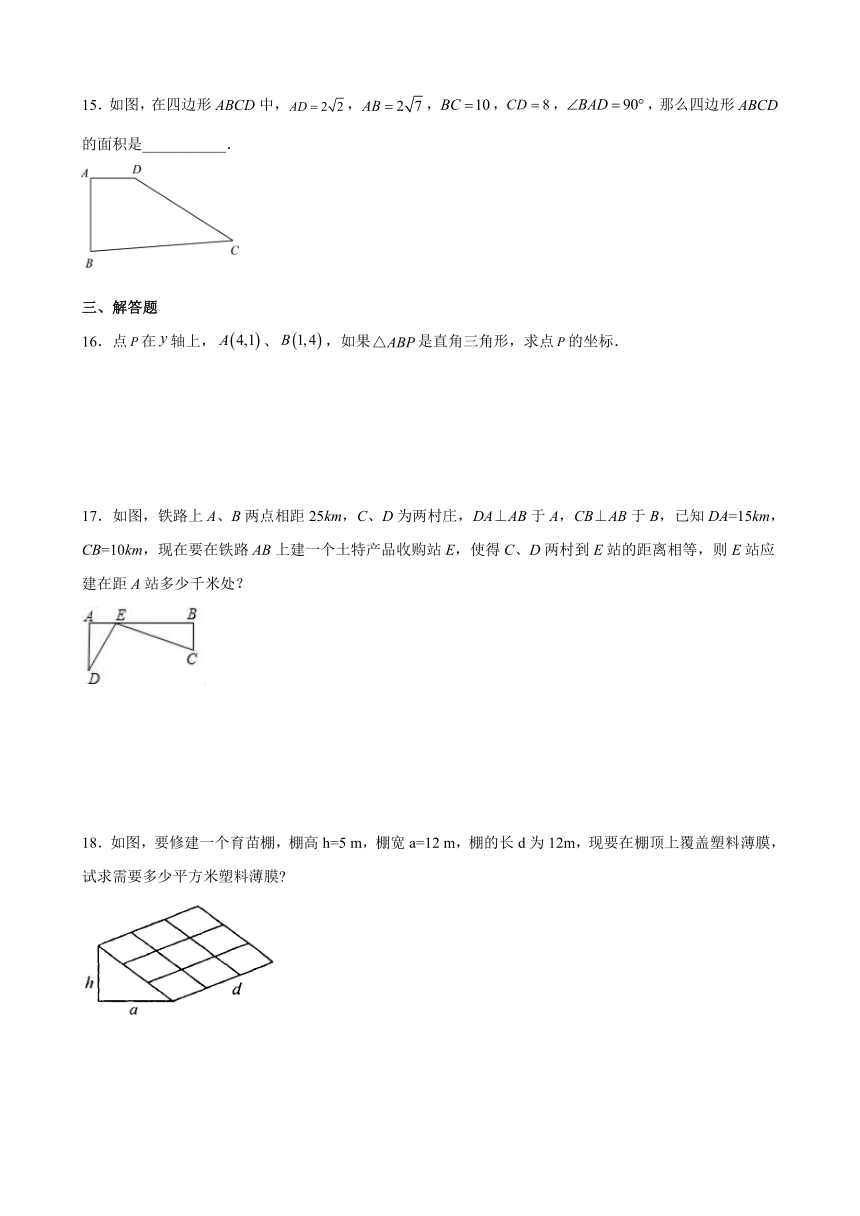
15.如图,在四边形ABCD中,,,,,,那么四边形ABCD的面积是___________.
三、解答题
16.点在轴上,、,如果是直角三角形,求点的坐标.
17.如图,铁路上A、B两点相距25km,C、D为两村庄,DA⊥AB于A,CB⊥AB于B,已知DA=15km,CB=10km,现在要在铁路AB上建一个土特产品收购站E,使得C、D两村到E站的距离相等,则E站应建在距A站多少千米处?
18.如图,要修建一个育苗棚,棚高h=5
m,棚宽a=12
m,棚的长d为12m,现要在棚顶上覆盖塑料薄膜,
试求需要多少平方米塑料薄膜
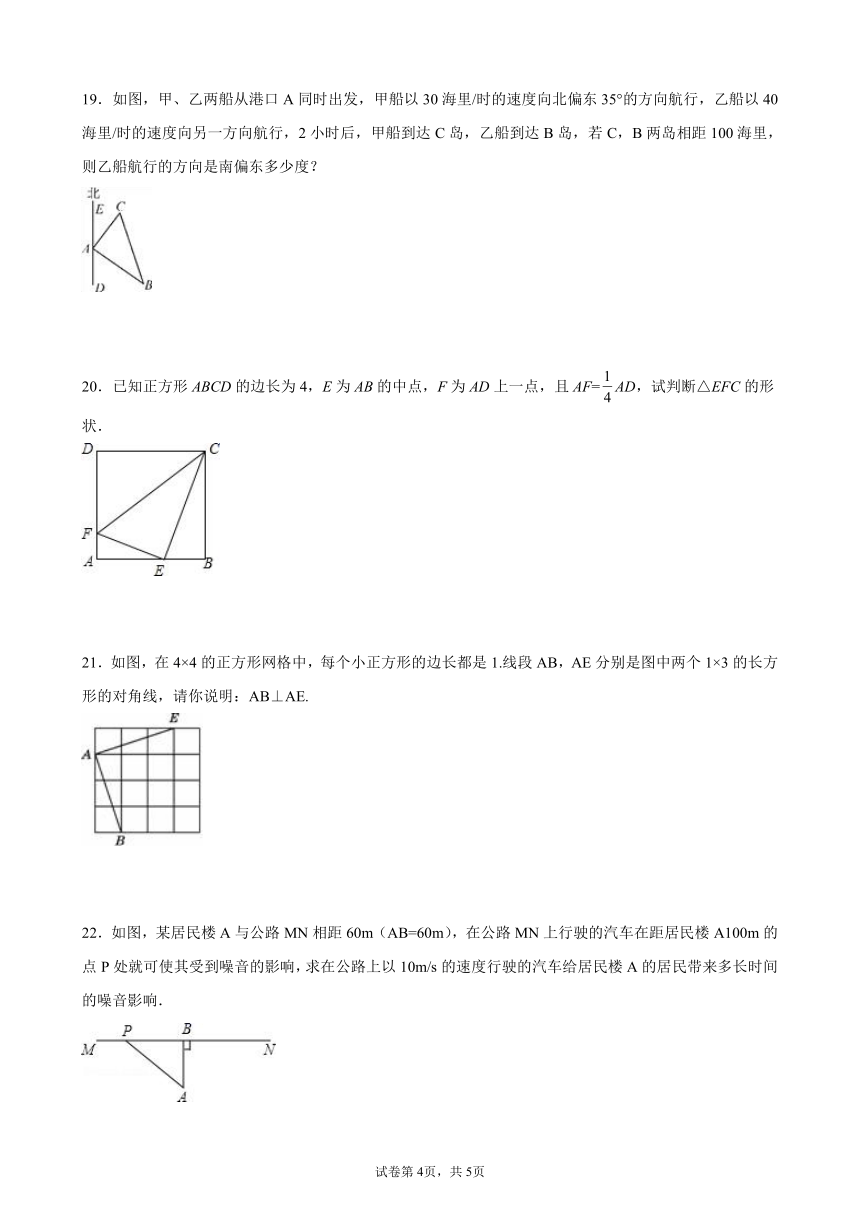
19.如图,甲、乙两船从港口A同时出发,甲船以30海里/时的速度向北偏东35°的方向航行,乙船以40海里/时的速度向另一方向航行,2小时后,甲船到达C岛,乙船到达B岛,若C,B两岛相距100海里,则乙船航行的方向是南偏东多少度?
20.已知正方形ABCD的边长为4,E为AB的中点,F为AD上一点,且AF=AD,试判断△EFC的形状.
21.如图,在4×4的正方形网格中,每个小正方形的边长都是1.线段AB,AE分别是图中两个1×3的长方形的对角线,请你说明:AB⊥AE.
22.如图,某居民楼A与公路MN相距60m(AB=60m),在公路MN上行驶的汽车在距居民楼A100m的点P处就可使其受到噪音的影响,求在公路上以10m/s的速度行驶的汽车给居民楼A的居民带来多长时间的噪音影响.
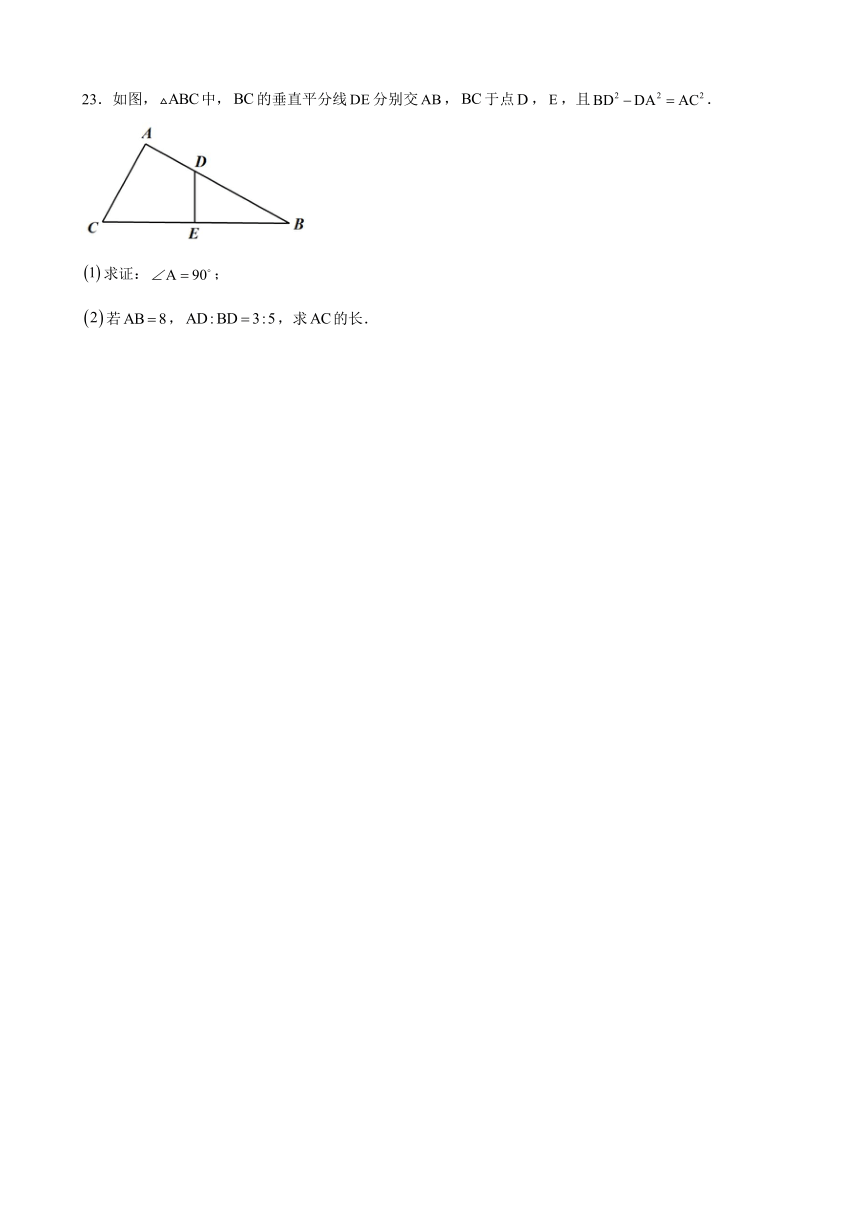
23.如图,中,的垂直平分线分别交,于点,,且.
求证:;
若,,求的长.
试卷第1页,共3页
参考答案
1.B
【解析】∵,
∴a2+b2=c2,
∴该三角形为直角三角形.
故选B.
2.B
【解析】∵,
根据绝对值、偶次方的非负性质,
∴c
=13,b=12,a=5,
∵52+122=132,
∴△ABC是以c为斜边的直角三角形.
故选:B.
3.C
【解析】解:如图,∵AD是中线,AB=10,BC=16,
∴BD=BC=8,
∵62+82=102,即BD2+AD2=AB2,
∴△ABD是直角三角形,即AD⊥BC,
又∵BD=CD,
∴AC=AB=10.
故选C.
4.C
【解析】A.AB2=1+36=37,AC2=16+25=41,BC2=1+9=10,37+10≠41,不可以构成直角三角形;
B.AD2=16+16=32,AG2=9+36=45,DG2=1+4=5,32+5≠45,不可以构成直角三角形;
C.BE2=36+16=52,BF2=25+25=50,EF2=1+1=2,50+2=52,可以构成直角三角形
D.BG2=25+9=34,BE2=36+16=52,GE2=9+1=10,34+10≠52,不可以构成直角三角形.
故选:C.
5.C
【解析】解:A.,
∴不能构成直角三角形,故选项错误;
B.∵,
∴不能构成直角三角形,故选项错误;
C.∵,
∴能构成直角三角形,故选项正确;
D.∵,
∴不能构成直角三角形,故选项错误.
故选C.
6.B
【解析】作点A关于CD的对称点A′,连接A′B,则A′B的长即为AP+BP的最小值,过点B作BE⊥AC,垂足为E,
∵CD=600m,BD=300m,AC=500m,
∴A′C=AC=500m,CE=BD=300m,CD=BE=600m,
∴A′E=A′C+CE=500+300=800m,
在Rt△A′CE中,,
故选B.
7.B
【解析】连接AC,则由勾股定理得AC=5米,因为AC2+DC2=AD2,所以∠ACD=90°.
这块草坪的面积=SRt△ABC+SRt△ACD=AB BC+AC DC=(3×4+5×12)=36米2.
故选B.
8.C
【解析】∵点A,B的纵坐标相等,
∴AB∥x轴,
∵点C到AB距离为5,AB=10,
∴点C在平行于AB的两条直线上,
∴过点A的垂线与那两条直线有2个交点,过点B的垂线与那两条直线有2个交点,以AB为直径的圆与那两条直线有只有2个交点(这两个两点在线段AB的垂直平分线上),
∴满足条件的C点共,6个.
故选C.
9.
【解析】原式可变形为
∴
∴
∴三角形为直角三角形
根据三角形的面积有
解得
故答案为:.
10.6
【解析】△ABC的面积为:×4×3=6.
故答案为6.
11.108
【解析】∵在△ABC中,三条边的长度分别为9、12、15,
∵92+122=152,
∴△ABC是直角三角形,
∴用两个这样的三角形所拼成的长方形的面积是2××9×12=108
12.12
【解析】设AE=x千米,则BE=(36-x)千米,
在Rt△AEC中,CE2=AE2+AC2=x2+242,在Rt△BED中,
DE2=BE2+BD2=+122,
∵CE=ED,∴x2+242=+122,解得x=12,所以E站应建在距A站12千米的地方,能使蔬菜基地C,D到E的距离相等,故答案为12.
13.20
【解析】在Rt△ABC中,AC=30m,AB=50m;
据勾股定理可得:BC==40(m),
故小汽车的速度为v==20m/s.
14.17
【解析】利用平移线段,把楼梯的横竖向下向右平移,构成一个直角三角形的两直角边;
则另一直角边长==12,所以地毯的长度为12+5=17米
故答案为17
15.+24
【解析】解:连结BD,
∵,
∴,
∵,,
∴BD=6,
∵BD2=36,CD2=64,BC2=100,
BD2+CD2=BC2,
∴∠BDC=90°,
S△ABD=,
S△BDC=,
四边形ABCD的面积是=
S△ABD+
S△BDC=+24
故答案为:+24.
16.点的坐标为或
【解析】设点的坐标为,分两种情况:
①当点为直角顶点时,点在轴正半轴,
作轴于,轴于,轴于,如图所示:
由勾股定理,得,
即,解得,
∴点的坐标为.
②当点为直角顶点时,点在轴负半轴,作轴于,轴于,如图所示:
由勾股定理,得,
即,解得,
∴点的坐标为.
综上所述,如果是直角三角形,那么点的坐标为或.
17.E点应建在距A站10千米处.
【解析】解:设AE=xkm,
∵C、D两村到E站的距离相等,∴DE=CE,即DE2=CE2,
由勾股定理,得152+x2=102+(25﹣x)2,x=10.
故:E点应建在距A站10千米处.
18.156
m2.
【解析】棚高h=5
m,棚宽a=12
m,设棚顶的宽为b,
则m
棚的长d为12m
19.乙船航行的方向为南偏东55°.
【解析】由题意可知,在△ABC中,AC=30×2=60,AB=40×2=80,BC=100,
∴AC2=3600,AB2=6400,BC2=10000,
∴AC2+AB2=BC2,
∴∠CAB=90°,
又∵∠EAD=180°,∠EAC=35°,
∴∠DAB=90°-∠CAE=90°-35°=55°,
∴乙船航行的方向为南偏东55°.
20.△EFC为直角三角形,理由见解析
【解析】解:△EFC为直角三角形.
∵正方形ABCD的边长为4,AF=AD
∴AF=1,FD=3,DC=BC=4,
∵E为AB的中点,
∴AE=EB=2;
在Rt△AEF中,EF=;
在Rt△DFC中,FC==5;
在Rt△EBC中,EC==2.
∴EC2+EF2=FC2,
∴△EFC是直角三角形.
21.△ABE是直角三角形,且∠BAE=90°,即AB⊥AE
【解析】如图,连接BE.因为AE2=12+32=10,AB2=12+32=10,BE2=22+42=20,所以AE2+AB2=BE2,所以△ABE是直角三角形,且∠BAE=90°,即AB⊥AE.
22.16秒
【解析】如图,设汽车行驶到点P′处噪音影响结束,连接AP′,则AP′=AP.
∵由勾股定理得到:PB==80,
∴PP′=2PB=2×80=160米,
∴影响时间为160÷10=16秒,
答:影响时间为16秒.
23.(1)见解析;(2)4
【解析】证明:连结.
的垂直平分线分别交,于点,,
.
,
,
,
是直角三角形,且.
解:,,
,,
,
.
答案第1页,共2页
答案第1页,共2页
17.3勾股定理(3)-同步练习
时间:60分钟
一、单选题
1.若三角形的三边长分别为,,,且满足,则此三角形中最大的角是(
)
A.锐角
B.直角
C.钝角
D.无法确定
2.已知,,是三角形的三边长,且,那么此三角形是(
)
A.以为斜边的直角三角形
B.以为斜边的直角三角形
C.等腰直角三角形
D.锐角三角形
3.中,,,BC边上的中线,则AC的长是(
).
A.6
B.8
C.10
D.16
4.如图:在一个边长为1的小正方形组成的方格稿纸上,有A、B、C、D、E、F、G七个点,则在下列任选三个点的方案中可以构成直角三角形的是( )
A.点A、点B、点C
B.点A、点D、点G
C.点B、点E、点F
D.点B、点G、点E
5.下列长度的各组线段能组成一个直角三角形的是(
)
A.
B.
C.
D.
6.如图,牧童家在B处,A、B两处相距河岸的距离AC、BD分别为500m和300m,且C、D两处的距离为600m,天黑牧童从A处将牛牵到河边去饮水,在赶回家,那么牧童最少要走(
)
A.800m
B.1000m
C.1200m
D.1500m
7.如图1,园丁住宅小区有一块草坪如图所示.已知AB=3米,BC=4米,CD=12米,DA=13米,且AB⊥BC,这块草坪的面积是(
)
A.24米2
B.36米2
C.48米2
D.72米2
8.在平面直角坐标系中,点A的坐标为(1,1),点B的坐标为(11,1),点C到直线AB的距离为5,且△ABC是直角三角形,则满足条件的C点有( )
A.4个
B.5个
C.6个
D.8个
二、填空题
9.一个三角形的三边长a,b,c满足,则这个三角形最长边上的高为________.
10.将△ABC放在每个小正方形的边长为1的网格中,点A、B、C均落在格点上,ABC的面积等于________;
11.在△中,若三边长分别为9、12、15,则以两个这样的三角形拼成的长方形的面积为______.
12.如图,在东西走向的铁路上有A、B两站(视为直线上的两点)相距36千米,在A、B的正北分别有C、D两个蔬菜基地,其中C到A站的距离为24千米,D到B站的距离为12千米,现要在铁路AB上建一个蔬菜加工厂E,使蔬菜基地C、D到E的距离相等,则E站应建在距A站_____千米的地方.
13.如图,一辆小汽车在一条城市街路上直道行驶,某一时刻刚好行驶到路对面车速检测仪A处的正前方30m的C处,过了2s后,测得小汽车与车速检测仪间的距离为50m,则这辆小汽车的速度是__m/s.
14.在高5cm,长13cm的一段台阶上铺上地毯,台阶的剖面如图所示,地毯的长度至少需要______m.
15.如图,在四边形ABCD中,,,,,,那么四边形ABCD的面积是___________.
三、解答题
16.点在轴上,、,如果是直角三角形,求点的坐标.
17.如图,铁路上A、B两点相距25km,C、D为两村庄,DA⊥AB于A,CB⊥AB于B,已知DA=15km,CB=10km,现在要在铁路AB上建一个土特产品收购站E,使得C、D两村到E站的距离相等,则E站应建在距A站多少千米处?
18.如图,要修建一个育苗棚,棚高h=5
m,棚宽a=12
m,棚的长d为12m,现要在棚顶上覆盖塑料薄膜,
试求需要多少平方米塑料薄膜
19.如图,甲、乙两船从港口A同时出发,甲船以30海里/时的速度向北偏东35°的方向航行,乙船以40海里/时的速度向另一方向航行,2小时后,甲船到达C岛,乙船到达B岛,若C,B两岛相距100海里,则乙船航行的方向是南偏东多少度?
20.已知正方形ABCD的边长为4,E为AB的中点,F为AD上一点,且AF=AD,试判断△EFC的形状.
21.如图,在4×4的正方形网格中,每个小正方形的边长都是1.线段AB,AE分别是图中两个1×3的长方形的对角线,请你说明:AB⊥AE.
22.如图,某居民楼A与公路MN相距60m(AB=60m),在公路MN上行驶的汽车在距居民楼A100m的点P处就可使其受到噪音的影响,求在公路上以10m/s的速度行驶的汽车给居民楼A的居民带来多长时间的噪音影响.
23.如图,中,的垂直平分线分别交,于点,,且.
求证:;
若,,求的长.
试卷第1页,共3页
参考答案
1.B
【解析】∵,
∴a2+b2=c2,
∴该三角形为直角三角形.
故选B.
2.B
【解析】∵,
根据绝对值、偶次方的非负性质,
∴c
=13,b=12,a=5,
∵52+122=132,
∴△ABC是以c为斜边的直角三角形.
故选:B.
3.C
【解析】解:如图,∵AD是中线,AB=10,BC=16,
∴BD=BC=8,
∵62+82=102,即BD2+AD2=AB2,
∴△ABD是直角三角形,即AD⊥BC,
又∵BD=CD,
∴AC=AB=10.
故选C.
4.C
【解析】A.AB2=1+36=37,AC2=16+25=41,BC2=1+9=10,37+10≠41,不可以构成直角三角形;
B.AD2=16+16=32,AG2=9+36=45,DG2=1+4=5,32+5≠45,不可以构成直角三角形;
C.BE2=36+16=52,BF2=25+25=50,EF2=1+1=2,50+2=52,可以构成直角三角形
D.BG2=25+9=34,BE2=36+16=52,GE2=9+1=10,34+10≠52,不可以构成直角三角形.
故选:C.
5.C
【解析】解:A.,
∴不能构成直角三角形,故选项错误;
B.∵,
∴不能构成直角三角形,故选项错误;
C.∵,
∴能构成直角三角形,故选项正确;
D.∵,
∴不能构成直角三角形,故选项错误.
故选C.
6.B
【解析】作点A关于CD的对称点A′,连接A′B,则A′B的长即为AP+BP的最小值,过点B作BE⊥AC,垂足为E,
∵CD=600m,BD=300m,AC=500m,
∴A′C=AC=500m,CE=BD=300m,CD=BE=600m,
∴A′E=A′C+CE=500+300=800m,
在Rt△A′CE中,,
故选B.
7.B
【解析】连接AC,则由勾股定理得AC=5米,因为AC2+DC2=AD2,所以∠ACD=90°.
这块草坪的面积=SRt△ABC+SRt△ACD=AB BC+AC DC=(3×4+5×12)=36米2.
故选B.
8.C
【解析】∵点A,B的纵坐标相等,
∴AB∥x轴,
∵点C到AB距离为5,AB=10,
∴点C在平行于AB的两条直线上,
∴过点A的垂线与那两条直线有2个交点,过点B的垂线与那两条直线有2个交点,以AB为直径的圆与那两条直线有只有2个交点(这两个两点在线段AB的垂直平分线上),
∴满足条件的C点共,6个.
故选C.
9.
【解析】原式可变形为
∴
∴
∴三角形为直角三角形
根据三角形的面积有
解得
故答案为:.
10.6
【解析】△ABC的面积为:×4×3=6.
故答案为6.
11.108
【解析】∵在△ABC中,三条边的长度分别为9、12、15,
∵92+122=152,
∴△ABC是直角三角形,
∴用两个这样的三角形所拼成的长方形的面积是2××9×12=108
12.12
【解析】设AE=x千米,则BE=(36-x)千米,
在Rt△AEC中,CE2=AE2+AC2=x2+242,在Rt△BED中,
DE2=BE2+BD2=+122,
∵CE=ED,∴x2+242=+122,解得x=12,所以E站应建在距A站12千米的地方,能使蔬菜基地C,D到E的距离相等,故答案为12.
13.20
【解析】在Rt△ABC中,AC=30m,AB=50m;
据勾股定理可得:BC==40(m),
故小汽车的速度为v==20m/s.
14.17
【解析】利用平移线段,把楼梯的横竖向下向右平移,构成一个直角三角形的两直角边;
则另一直角边长==12,所以地毯的长度为12+5=17米
故答案为17
15.+24
【解析】解:连结BD,
∵,
∴,
∵,,
∴BD=6,
∵BD2=36,CD2=64,BC2=100,
BD2+CD2=BC2,
∴∠BDC=90°,
S△ABD=,
S△BDC=,
四边形ABCD的面积是=
S△ABD+
S△BDC=+24
故答案为:+24.
16.点的坐标为或
【解析】设点的坐标为,分两种情况:
①当点为直角顶点时,点在轴正半轴,
作轴于,轴于,轴于,如图所示:
由勾股定理,得,
即,解得,
∴点的坐标为.
②当点为直角顶点时,点在轴负半轴,作轴于,轴于,如图所示:
由勾股定理,得,
即,解得,
∴点的坐标为.
综上所述,如果是直角三角形,那么点的坐标为或.
17.E点应建在距A站10千米处.
【解析】解:设AE=xkm,
∵C、D两村到E站的距离相等,∴DE=CE,即DE2=CE2,
由勾股定理,得152+x2=102+(25﹣x)2,x=10.
故:E点应建在距A站10千米处.
18.156
m2.
【解析】棚高h=5
m,棚宽a=12
m,设棚顶的宽为b,
则m
棚的长d为12m
19.乙船航行的方向为南偏东55°.
【解析】由题意可知,在△ABC中,AC=30×2=60,AB=40×2=80,BC=100,
∴AC2=3600,AB2=6400,BC2=10000,
∴AC2+AB2=BC2,
∴∠CAB=90°,
又∵∠EAD=180°,∠EAC=35°,
∴∠DAB=90°-∠CAE=90°-35°=55°,
∴乙船航行的方向为南偏东55°.
20.△EFC为直角三角形,理由见解析
【解析】解:△EFC为直角三角形.
∵正方形ABCD的边长为4,AF=AD
∴AF=1,FD=3,DC=BC=4,
∵E为AB的中点,
∴AE=EB=2;
在Rt△AEF中,EF=;
在Rt△DFC中,FC==5;
在Rt△EBC中,EC==2.
∴EC2+EF2=FC2,
∴△EFC是直角三角形.
21.△ABE是直角三角形,且∠BAE=90°,即AB⊥AE
【解析】如图,连接BE.因为AE2=12+32=10,AB2=12+32=10,BE2=22+42=20,所以AE2+AB2=BE2,所以△ABE是直角三角形,且∠BAE=90°,即AB⊥AE.
22.16秒
【解析】如图,设汽车行驶到点P′处噪音影响结束,连接AP′,则AP′=AP.
∵由勾股定理得到:PB==80,
∴PP′=2PB=2×80=160米,
∴影响时间为160÷10=16秒,
答:影响时间为16秒.
23.(1)见解析;(2)4
【解析】证明:连结.
的垂直平分线分别交,于点,,
.
,
,
,
是直角三角形,且.
解:,,
,,
,
.
答案第1页,共2页
答案第1页,共2页
同课章节目录
- 第十二章 分式和分式方程
- 12.1 分式
- 12.2 分式的乘除
- 12.3 分式的加减
- 12.4 分式方程
- 12.5 分式方程的应用
- 第十三章 全等三角形
- 13.1 命题与证明
- 13.2 全等图形
- 13.3 全等三角形的判定
- 13.4 三角形的尺规作图
- 第十四章 实数
- 14.1 平方根
- 14.2 立方根
- 14.3 实数
- 14.4 近似数
- 14.5 用计算器求平方根与立方根
- 第十五章 二次根式
- 15.1 二次根式
- 15.2 二次根式的乘除
- 15.3 二次根式的加减
- 15.4 二次根式的混合
- 第十六章 轴对称和中心对称
- 16.1 轴对称
- 16.2 线段的垂直平分
- 16.3 角的平分线
- 16.4 中心对称图形
- 16.5 利用图形的平移、旋转和轴对称设计图案
- 第十七章 特殊三角形
- 17.1 等腰三角形
- 17.2 直角三角形
- 17.3 勾股定理
- 17.4 直角三角形全等的判定
- 17.5 反证法
