17.3勾股定理-同步练习-2021-2022学年冀教版八年级数学上册(word版含答案)
文档属性
| 名称 | 17.3勾股定理-同步练习-2021-2022学年冀教版八年级数学上册(word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 390.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-05 00:00:00 | ||
图片预览




文档简介
2021-2022学年八年级数学上册(冀教版)
17.3勾股定理(1)-同步练习
时间:60分钟
一、单选题
1.若直角三角形的一条直角边长为9,斜边长为10,则另一条直角边长为(
).
A.1
B.
C.19
D.3
2.在平面直角坐标系中,点P(﹣x,2x)到原点O的距离等于5,则x的值是( )
A.±1
B.1
C.
D.±
3.如图,在中,,正方形的面积分别为25和144,则的长度为(
)
A.13
B.169
C.12
D.5
4.如图,正方形网格中的,若小方格边长为,则的形状为(
)
A.直角三角形
B.锐角三角形
C.钝角三角形
D.以上答案都不对
5.在中,,,则(
).
A.100
B.200
C.300
D.400
6.直角三角形的两条直角边为a、b,斜边为c,斜边上的高为h,下列结论:①a2+b2=c2;②ab=ch;③.其中正确的是( )
A.①②③
B.①
C.①②
D.①③
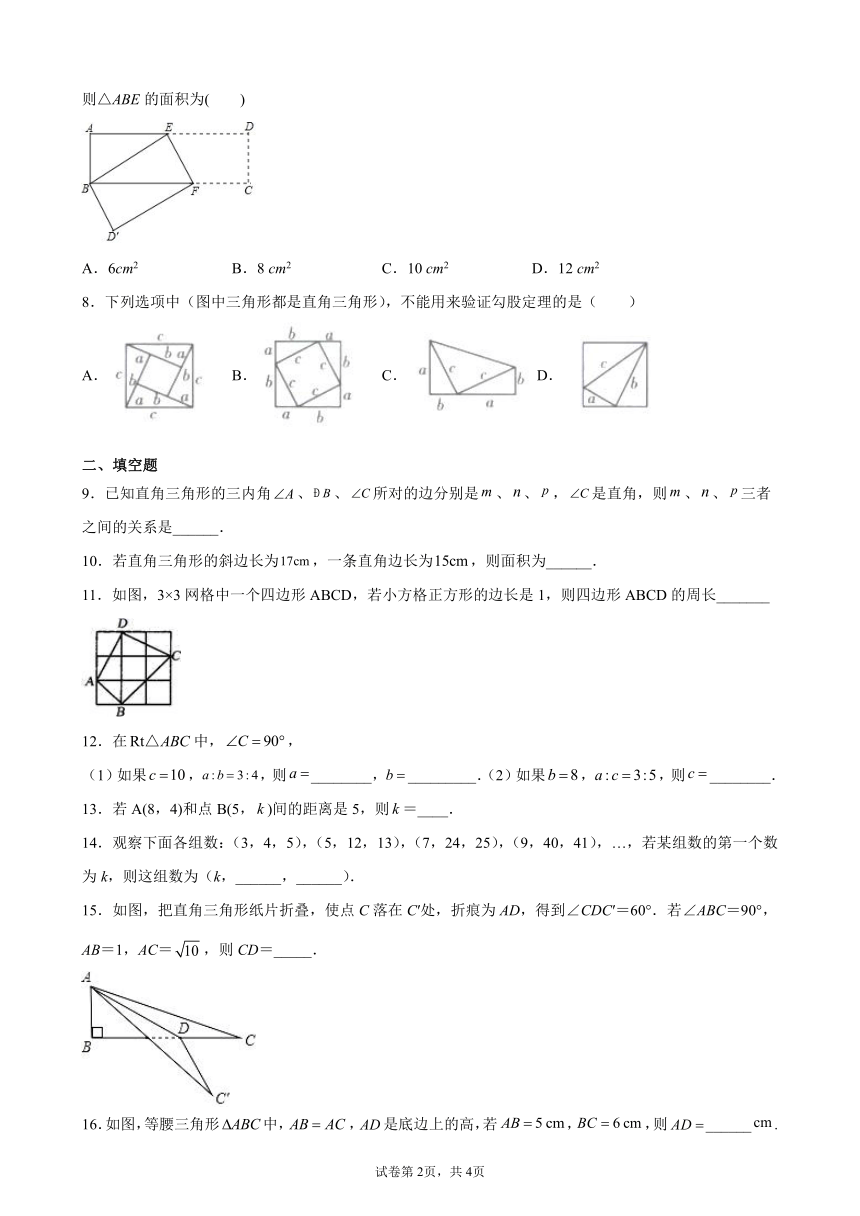
7.已知,如图,长方形ABCD中,AB=3cm,AD=9cm,将此长方形折叠,使点B与点D重合,折痕为EF,则△ABE的面积为( )
A.6cm2
B.8
cm2
C.10
cm2
D.12
cm2
8.下列选项中(图中三角形都是直角三角形),不能用来验证勾股定理的是(
)
A.
B.
C.
D.
二、填空题
9.已知直角三角形的三内角、、所对的边分别是、、,是直角,则、、三者之间的关系是______.
10.若直角三角形的斜边长为,一条直角边长为,则面积为______.
11.如图,3×3网格中一个四边形ABCD,若小方格正方形的边长是1,则四边形ABCD的周长_______
12.在中,,
(1)如果,,则________,_________.(2)如果,,则________.
13.若A(8,4)和点B(5,)间的距离是5,则=____.
14.观察下面各组数:(3,4,5),(5,12,13),(7,24,25),(9,40,41),…,若某组数的第一个数为k,则这组数为(k,______,______).
15.如图,把直角三角形纸片折叠,使点C落在C′处,折痕为AD,得到∠CDC′=60°.若∠ABC=90°,AB=1,AC=,则CD=_____.
16.如图,等腰三角形中,,是底边上的高,若,,则______.
三、解答题
17.已知等腰三角形腰长是10,底边长是16,求这个等腰三角形的面积.
18.已知A(,),B(4,),C(1,2),判定ABC的形状.
19.如图是一块地,已知AD=4,CD=3,AB=13,BC=12,且CD⊥AD,求这块地的面积.
20.如图,在4×4的正方形网格中,每个小正方形的顶点称为格点,每个小正方形的边长均为1cm.请在网格内绘制一个三角形
,三边长分别为cm,cm,cm,并求此三角形的面积.
21.如图,将矩形沿折叠,使点落在边的点处,已知,.求的长.
22.在中,,,,求斜边上的高.
23.在平面直角坐标系中,已知点,点,点是轴上一点,若是等腰三角形,试求点的坐标.
24.观察下列勾股数:3,4,5;5,12,13;7,24,25;9,40,41;…;,,.
根据你发现的规律,请求出:
(1)当时,,的值;
(2)当时,,的值.
试卷第1页,共3页
参考答案
1.B
【解析】解:由勾股定理的变形公式可得:另一直角边长==.
故选B.
2.D
【解析】解:∵点P(﹣x,2x)到原点O的距离等于5,
∴x2+4x2=25,解得x=±.
故选:D.
3.A
【解析】解:∵在Rt△ABC中,由勾股定理得:AC2+BC2=AB2,
又∵AC2=144,BC2=25,
∴AB2=25+144=169,
∴AB==13.
故选:A.
4.A
【解析】解:∵正方形小方格边长为1,
∴BC=,
AC=,
AB=,
在△ABC中,
∵BC2+AC2=32+18=50,AB2=50,
∴BC2+AC2=AB2,
∴△ABC是直角三角形.
故选:A.
5.C
【解析】解:∵在中,且,
∴AB为的斜边,
∴根据勾股定理得:,
∴,
故选:C.
6.A
【解析】解:∵直角三角形的两条直角边为a、b,斜边为c,斜边上的高为h,
∴由勾股定理可知:a2+b2=c2,①正确;
这个直角三角形的面积=ab=ch,
∴ab=ch,②正确;
∴a2b2=c2h2,
∴,③正确.
故选A.
7.A
【解析】解:∵将此长方形折叠,使点B与点D重合,
∴BE=ED.
∵AD=9cm=AE+DE=AE+BE.
∴BE=9﹣AE,
根据勾股定理可知:AB2+AE2=BE2.
∴32+AE2=(9﹣AE)2.
解得:AE=4cm.
∴△ABE的面积为:×3×4=6(cm2).
故选:A.
8.D
【解析】A,B,C都可以利用图形面积得出a,b,c的关系,即可证明勾股定理;故A,B,C选项不符合题意;
D、不能利用图形面积证明勾股定理,故此选项正确.
故选D.
9.
【解析】解:在直角三角形中,是直角,
∴;
故答案为:.
10.
【解析】∵直角三角形的斜边长为,一条直角边长为,
∴另一直角边长为:cm,
∴直角三角形面积为:=60
,
故答案为:.
11.3+2
【解析】解:由于小方格正方形的边长为1,
由勾股定理从图中知,
四边形ABCD的周长为+++=3+2.
12.6,
8;
10.
【解析】解:在中,,则是斜边;
(1)∵,,
设,,
∴,
∴,
∴,;
故答案为:6,8;
(2)∵,,
设,,
∴,
∴,
∴.
故答案为:10.
13.8或0
【解析】根据两点的距离公式得(8-5)2+(k-4)2=52,解得k=8或0,
故答案为:8或0.
14.
【解析】由已给四组数可发现:,,,……,即
,,,……,即
故答案为:;
15.
【解析】解:∵把直角三角形纸片折叠,使点C落在C′处,折痕为AD,∠CDC′=60°,
∴∠ADC=150°,
∴∠ADB=30°,
∴AD=2AB=2,
∵∠ABC=90°,
∴BC=,BD=,
∴CD=BC﹣BD=.
故答案为:.
16.4
【解析】∵等腰三角形中,,是底边上的高,
∴AD是△ABC中BC边上的中线,
∴BD=DC,
∵,
∴DB=3cm,
∵,
∴,
故答案为4.
17.48
【解析】如图,△ABC中,AB=
AC=
10,BC=
16,过点A作AD⊥BC于D,
∴BD=CD=BC=×16=8
∴∠ADB=90°
.∴
AD===6
∴S
=BC×AD=×16×6=48
∴这个等腰三角形的面积是48
18.ABC是等腰直角三角形,见解析
【解析】利用两点的距离公式,可得
AB=
,
AC=
,
BC=
,
所以AC=BC,AB2=AC2+BC2
所以△ABC是直角三角形,
综上所述,△ABC是等腰直角三角形.
19.
【解析】解:连接AC,
∵CD⊥AD
∴∠ADC=90°,
∵AD=4,CD=3,
∴AC2=AD2+CD2=42+32=25,
又∵AC>0,
∴AC=5,
又∵BC=12,AB=13,
∴AC2+BC2=52+122=169,
又∵AB2=169,
∴AC2+BC2=AB2,
∴∠ACB=90°,
∴S四边形ABCD=S△ABC-S△ADC=30-6=
20.3.5(cm)
【解析】如图所示.
如图△DEF为所求.
S△DEF==3.5(cm).
21.3.
【解析】设的长为,则.
∵折叠后的图形是,
∴,.
∵,∴.
∵四边形是矩形,∴.
在中,,
∴.
在中,,
∴,解得,
∴的长为3.
22.2
【解析】∵BC:AC=1:2,
∴设BC=k,AC=2k,
由勾股定理得,BC2+AC2=AB2,
即k2+(2k)2=52,
解得k=,
所以,BC=,AC=2,
设AB边长的高为h,
则S△ABC=×5h=××2,
解得h=2,
即斜边AB上的高为2.
23.、、或
【解析】设点的坐标为,
若,则,解得,,
∴.
若,则.解得.
∴.
若,则.解得,,
∴或.
综上、、或.
24.(1),;(2),.
【解析】(1)通过观察可知,,
所以,解得,
因此.
(2)根据题意,得,
即,解得,.
答案第1页,共2页
答案第1页,共2页
17.3勾股定理(1)-同步练习
时间:60分钟
一、单选题
1.若直角三角形的一条直角边长为9,斜边长为10,则另一条直角边长为(
).
A.1
B.
C.19
D.3
2.在平面直角坐标系中,点P(﹣x,2x)到原点O的距离等于5,则x的值是( )
A.±1
B.1
C.
D.±
3.如图,在中,,正方形的面积分别为25和144,则的长度为(
)
A.13
B.169
C.12
D.5
4.如图,正方形网格中的,若小方格边长为,则的形状为(
)
A.直角三角形
B.锐角三角形
C.钝角三角形
D.以上答案都不对
5.在中,,,则(
).
A.100
B.200
C.300
D.400
6.直角三角形的两条直角边为a、b,斜边为c,斜边上的高为h,下列结论:①a2+b2=c2;②ab=ch;③.其中正确的是( )
A.①②③
B.①
C.①②
D.①③
7.已知,如图,长方形ABCD中,AB=3cm,AD=9cm,将此长方形折叠,使点B与点D重合,折痕为EF,则△ABE的面积为( )
A.6cm2
B.8
cm2
C.10
cm2
D.12
cm2
8.下列选项中(图中三角形都是直角三角形),不能用来验证勾股定理的是(
)
A.
B.
C.
D.
二、填空题
9.已知直角三角形的三内角、、所对的边分别是、、,是直角,则、、三者之间的关系是______.
10.若直角三角形的斜边长为,一条直角边长为,则面积为______.
11.如图,3×3网格中一个四边形ABCD,若小方格正方形的边长是1,则四边形ABCD的周长_______
12.在中,,
(1)如果,,则________,_________.(2)如果,,则________.
13.若A(8,4)和点B(5,)间的距离是5,则=____.
14.观察下面各组数:(3,4,5),(5,12,13),(7,24,25),(9,40,41),…,若某组数的第一个数为k,则这组数为(k,______,______).
15.如图,把直角三角形纸片折叠,使点C落在C′处,折痕为AD,得到∠CDC′=60°.若∠ABC=90°,AB=1,AC=,则CD=_____.
16.如图,等腰三角形中,,是底边上的高,若,,则______.
三、解答题
17.已知等腰三角形腰长是10,底边长是16,求这个等腰三角形的面积.
18.已知A(,),B(4,),C(1,2),判定ABC的形状.
19.如图是一块地,已知AD=4,CD=3,AB=13,BC=12,且CD⊥AD,求这块地的面积.
20.如图,在4×4的正方形网格中,每个小正方形的顶点称为格点,每个小正方形的边长均为1cm.请在网格内绘制一个三角形
,三边长分别为cm,cm,cm,并求此三角形的面积.
21.如图,将矩形沿折叠,使点落在边的点处,已知,.求的长.
22.在中,,,,求斜边上的高.
23.在平面直角坐标系中,已知点,点,点是轴上一点,若是等腰三角形,试求点的坐标.
24.观察下列勾股数:3,4,5;5,12,13;7,24,25;9,40,41;…;,,.
根据你发现的规律,请求出:
(1)当时,,的值;
(2)当时,,的值.
试卷第1页,共3页
参考答案
1.B
【解析】解:由勾股定理的变形公式可得:另一直角边长==.
故选B.
2.D
【解析】解:∵点P(﹣x,2x)到原点O的距离等于5,
∴x2+4x2=25,解得x=±.
故选:D.
3.A
【解析】解:∵在Rt△ABC中,由勾股定理得:AC2+BC2=AB2,
又∵AC2=144,BC2=25,
∴AB2=25+144=169,
∴AB==13.
故选:A.
4.A
【解析】解:∵正方形小方格边长为1,
∴BC=,
AC=,
AB=,
在△ABC中,
∵BC2+AC2=32+18=50,AB2=50,
∴BC2+AC2=AB2,
∴△ABC是直角三角形.
故选:A.
5.C
【解析】解:∵在中,且,
∴AB为的斜边,
∴根据勾股定理得:,
∴,
故选:C.
6.A
【解析】解:∵直角三角形的两条直角边为a、b,斜边为c,斜边上的高为h,
∴由勾股定理可知:a2+b2=c2,①正确;
这个直角三角形的面积=ab=ch,
∴ab=ch,②正确;
∴a2b2=c2h2,
∴,③正确.
故选A.
7.A
【解析】解:∵将此长方形折叠,使点B与点D重合,
∴BE=ED.
∵AD=9cm=AE+DE=AE+BE.
∴BE=9﹣AE,
根据勾股定理可知:AB2+AE2=BE2.
∴32+AE2=(9﹣AE)2.
解得:AE=4cm.
∴△ABE的面积为:×3×4=6(cm2).
故选:A.
8.D
【解析】A,B,C都可以利用图形面积得出a,b,c的关系,即可证明勾股定理;故A,B,C选项不符合题意;
D、不能利用图形面积证明勾股定理,故此选项正确.
故选D.
9.
【解析】解:在直角三角形中,是直角,
∴;
故答案为:.
10.
【解析】∵直角三角形的斜边长为,一条直角边长为,
∴另一直角边长为:cm,
∴直角三角形面积为:=60
,
故答案为:.
11.3+2
【解析】解:由于小方格正方形的边长为1,
由勾股定理从图中知,
四边形ABCD的周长为+++=3+2.
12.6,
8;
10.
【解析】解:在中,,则是斜边;
(1)∵,,
设,,
∴,
∴,
∴,;
故答案为:6,8;
(2)∵,,
设,,
∴,
∴,
∴.
故答案为:10.
13.8或0
【解析】根据两点的距离公式得(8-5)2+(k-4)2=52,解得k=8或0,
故答案为:8或0.
14.
【解析】由已给四组数可发现:,,,……,即
,,,……,即
故答案为:;
15.
【解析】解:∵把直角三角形纸片折叠,使点C落在C′处,折痕为AD,∠CDC′=60°,
∴∠ADC=150°,
∴∠ADB=30°,
∴AD=2AB=2,
∵∠ABC=90°,
∴BC=,BD=,
∴CD=BC﹣BD=.
故答案为:.
16.4
【解析】∵等腰三角形中,,是底边上的高,
∴AD是△ABC中BC边上的中线,
∴BD=DC,
∵,
∴DB=3cm,
∵,
∴,
故答案为4.
17.48
【解析】如图,△ABC中,AB=
AC=
10,BC=
16,过点A作AD⊥BC于D,
∴BD=CD=BC=×16=8
∴∠ADB=90°
.∴
AD===6
∴S
=BC×AD=×16×6=48
∴这个等腰三角形的面积是48
18.ABC是等腰直角三角形,见解析
【解析】利用两点的距离公式,可得
AB=
,
AC=
,
BC=
,
所以AC=BC,AB2=AC2+BC2
所以△ABC是直角三角形,
综上所述,△ABC是等腰直角三角形.
19.
【解析】解:连接AC,
∵CD⊥AD
∴∠ADC=90°,
∵AD=4,CD=3,
∴AC2=AD2+CD2=42+32=25,
又∵AC>0,
∴AC=5,
又∵BC=12,AB=13,
∴AC2+BC2=52+122=169,
又∵AB2=169,
∴AC2+BC2=AB2,
∴∠ACB=90°,
∴S四边形ABCD=S△ABC-S△ADC=30-6=
20.3.5(cm)
【解析】如图所示.
如图△DEF为所求.
S△DEF==3.5(cm).
21.3.
【解析】设的长为,则.
∵折叠后的图形是,
∴,.
∵,∴.
∵四边形是矩形,∴.
在中,,
∴.
在中,,
∴,解得,
∴的长为3.
22.2
【解析】∵BC:AC=1:2,
∴设BC=k,AC=2k,
由勾股定理得,BC2+AC2=AB2,
即k2+(2k)2=52,
解得k=,
所以,BC=,AC=2,
设AB边长的高为h,
则S△ABC=×5h=××2,
解得h=2,
即斜边AB上的高为2.
23.、、或
【解析】设点的坐标为,
若,则,解得,,
∴.
若,则.解得.
∴.
若,则.解得,,
∴或.
综上、、或.
24.(1),;(2),.
【解析】(1)通过观察可知,,
所以,解得,
因此.
(2)根据题意,得,
即,解得,.
答案第1页,共2页
答案第1页,共2页
同课章节目录
- 第十二章 分式和分式方程
- 12.1 分式
- 12.2 分式的乘除
- 12.3 分式的加减
- 12.4 分式方程
- 12.5 分式方程的应用
- 第十三章 全等三角形
- 13.1 命题与证明
- 13.2 全等图形
- 13.3 全等三角形的判定
- 13.4 三角形的尺规作图
- 第十四章 实数
- 14.1 平方根
- 14.2 立方根
- 14.3 实数
- 14.4 近似数
- 14.5 用计算器求平方根与立方根
- 第十五章 二次根式
- 15.1 二次根式
- 15.2 二次根式的乘除
- 15.3 二次根式的加减
- 15.4 二次根式的混合
- 第十六章 轴对称和中心对称
- 16.1 轴对称
- 16.2 线段的垂直平分
- 16.3 角的平分线
- 16.4 中心对称图形
- 16.5 利用图形的平移、旋转和轴对称设计图案
- 第十七章 特殊三角形
- 17.1 等腰三角形
- 17.2 直角三角形
- 17.3 勾股定理
- 17.4 直角三角形全等的判定
- 17.5 反证法
