16.4中心对称图形-同步练习-2021-2022学年八年级数学上册冀教版(word版含答案)
文档属性
| 名称 | 16.4中心对称图形-同步练习-2021-2022学年八年级数学上册冀教版(word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 460.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-05 00:00:00 | ||
图片预览



文档简介
2021-2022学年八年级数学上册(冀教版)
16.4中心对称图形-同步练习
时间:60分钟
一、单选题
1.下列图案中,是中心对称图形的是(
)
A.
B.
C.
D.
2.已知A、B两点关于原点对称,且A(3,4),则AB为( )
A.5
B.6
C.10
D.8
3.把图中阴影部分的小正方形移动一个,使它与其余四个阴影部分的正方形组成一个既是轴对称又是中心对称的新图形,这样的移法,正确的是( )
A.6→3
B.7→16
C.7→8
D.6→15
4.如图是一个中心对称图形,则此图形的对称中心为( )
A.A点
B.B点
C.C点
D.D点
5.如图,与关于成中心对称,不一定成立的结论是(
)
A.
B.
C.
D.
6.如图,四边形与四边形FGHE关于点O成中心对称,下列说法中错误的是(
)
A.
B.
C.
D.
7.如图,四边形ABCD与四边形FGHE关于一个点成中心对称,则这个点是( )
A.O1
B.O2
C.O3
D.O4
8.关于成中心对称的两个图形的性质,下列说法正确的是(
)
A.连接对应点的线段都经过对称中心,并且被对称中心平分
B.成中心对称的两个图形的对应线段不一定相等
C.对应点的连线不一定都经过对称中心
D.以上说法都不对
二、填空题
9.下列这些数字中有_____个是中心对称的图形.有_____个是轴对称的图形.
10.中心对称图形:如果一个图形绕着一个点旋转180°后,所得到的图形能够和原来的图形互相重合,那么这个图形叫做_____________,这个点叫_____________.
11.如图,是4×4正方形网格,把其中一个标有数字的白色小正方形涂黑,就可以使图中的黑色部分构成一个中心对称图形,则这个白色小正方形内的数字是_____.
12.如果两个图形的对应点连成的线段都经过某一点,并且被平分,则这两个图形一定关于这一点成____对称.
13.点
A(a,-2)与点
B(8,b)关于原点对称,则a
=___,b
=____.
14.点关于原点对称的点的坐标为______.
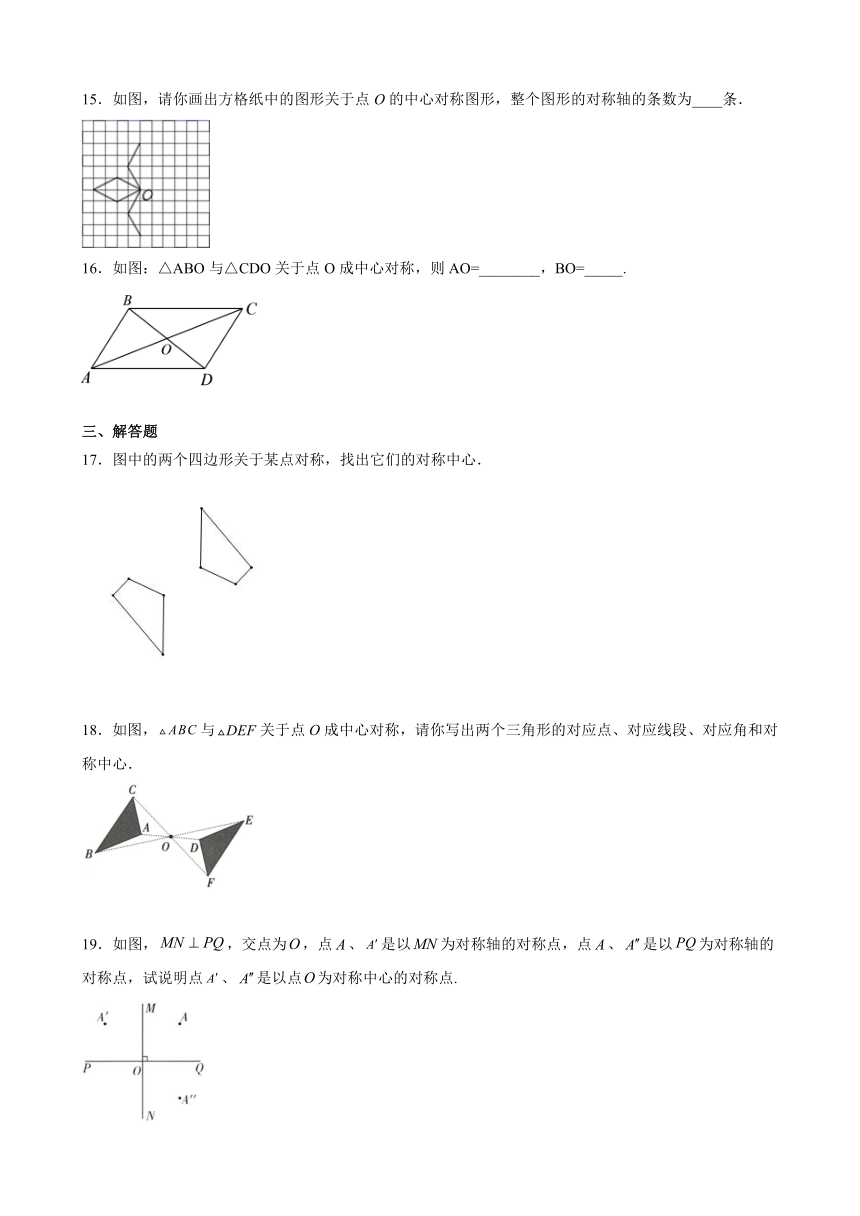
15.如图,请你画出方格纸中的图形关于点O的中心对称图形,整个图形的对称轴的条数为____条.
16.如图:△ABO与△CDO关于点O成中心对称,则AO=________,BO=_____.
三、解答题
17.图中的两个四边形关于某点对称,找出它们的对称中心.
18.如图,与关于点O成中心对称,请你写出两个三角形的对应点、对应线段、对应角和对称中心.
19.如图,,交点为,点、是以为对称轴的对称点,点、是以为对称轴的对称点,试说明点、是以点为对称中心的对称点.
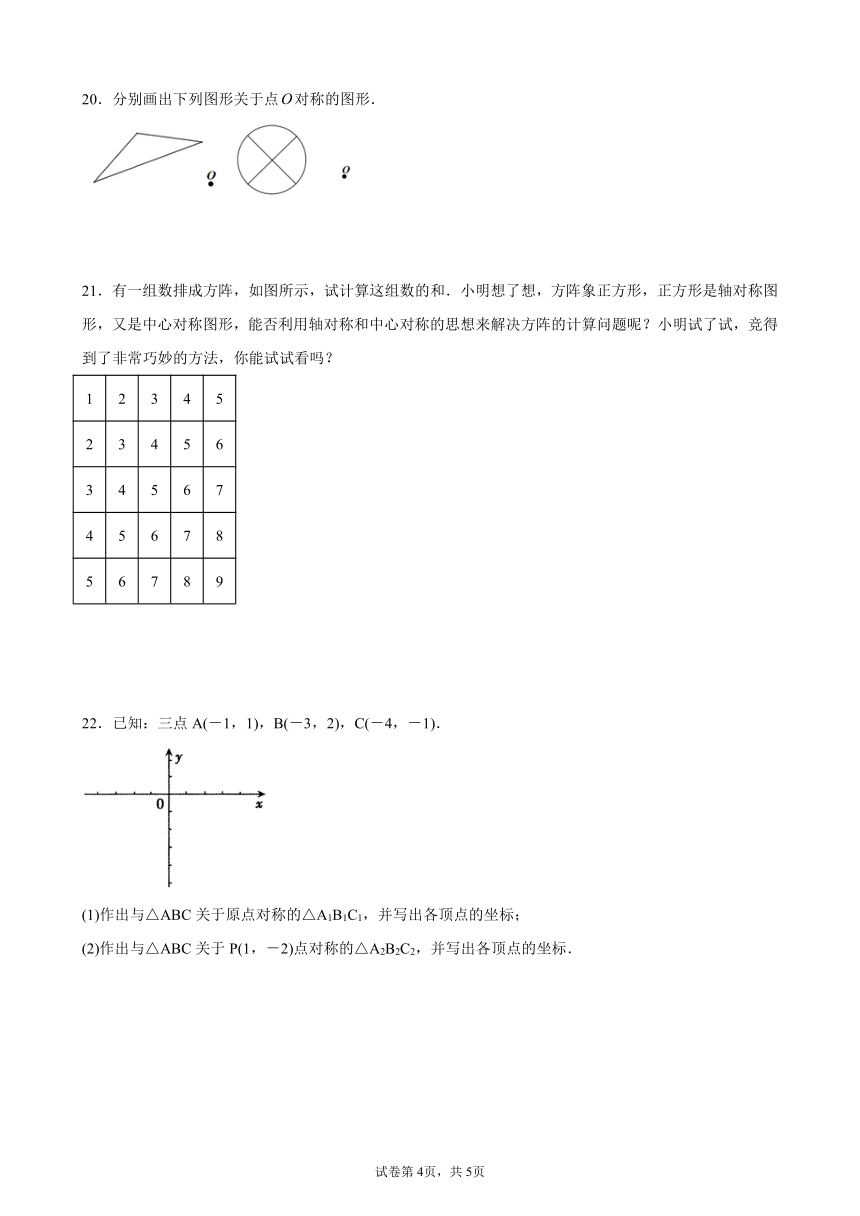
20.分别画出下列图形关于点对称的图形.
21.有一组数排成方阵,如图所示,试计算这组数的和.小明想了想,方阵象正方形,正方形是轴对称图形,又是中心对称图形,能否利用轴对称和中心对称的思想来解决方阵的计算问题呢?小明试了试,竞得到了非常巧妙的方法,你能试试看吗?
1
2
3
4
5
2
3
4
5
6
3
4
5
6
7
4
5
6
7
8
5
6
7
8
9
22.已知:三点A(-1,1),B(-3,2),C(-4,-1).
(1)作出与△ABC关于原点对称的△A1B1C1,并写出各顶点的坐标;
(2)作出与△ABC关于P(1,-2)点对称的△A2B2C2,并写出各顶点的坐标.
23.如图,在平面直角坐标系中,点,点,将绕着点旋转180°后得到.
(1)在图中画出;
(2)求点、点的对称点和的坐标;
(3)请直接写出和的数量关系和位置关系.
24.如图,点O是正六边形ABCDEF的中心.
(1)找出这个轴对称图形的对称轴;
(2)这个正六边形绕点O旋转多少度后能和原来的图形重合?
(3)如果换成其他的正多边形呢?能得到一般的结论吗?
试卷第1页,共3页
参考答案
1.B
【解析】略
2.C
【解析】B两点关于原点对称,且A(3,4),那么B;根据两点的距离公式可得AB=10
故选:C.
3.D
【解析】解:6→3
,能使它与其余四个阴影部分的正方形组成一个轴对称图形,但不是中心对称图形
,故不符合题意;
B.
7→16,能使它与其余四个阴影部分的正方形组成一个中心对称图形,但不是轴对称图形,故不符合题意;
C.
7→8
,能使它与其余四个阴影部分的正方形组成一个轴对称图形,但不是中心对称图形,故不符合题意;
D.
6→15,能使它与其余四个阴影部分的正方形组成一个既是轴对称又是中心对称的新图形,故符合题意;
故选D.
4.B
【解析】解:如图所示:
点A与点C是对应点,点D与点E是对应点,线段AC与DE相交于点B,
所以点B是对称中心.
故选B.
5.D
【解析】解:对应点的连线被对称中心平分,A,B正确;
成中心对称图形的两个图形是全等形,那么对应线段相等,C正确;
和不是对应角,D错误.
故选:D.
6.D
【解析】A.∵与关于点O成中心对称,
∴,同理可得,正确;
B.∵点B与点G关于点O成中心对称,
∴,正确;
C.∵与关于点O成中心对称,
∴,同理可得,正确;
D.∵点D与点E关于点O成中心对称,
∴,
∴错误,
故选:D.
7.A
【解析】如图,连接HC和DE交于O1,
故选A.
8.A
【解析】根据中心对称的性质:
A.
连接对应点的线段都经过对称中心,并且被对称中心平分,此选项正确;
B.
根据成中心对称的两个图形的对应线段一定相等,故此选项错误;
C.
根据对应点的连线一定都经过对称中心,故此选项错误;
D.
以上说法都不对,此选项错误.
故答案选:A.
9.5
4
【解析】略
10.中心对称图形;
对称中心.
【解析】解:∵把一个图形绕着一个点旋转180°后,所得到的图形能够和原来的图形互相重合,那么这个图形叫做中心对称图形,这个点叫对称中心.
∴答案为:中心对称图形;对称中心.
11.9
【解析】如图,把标有数字9的白色小正方形涂黑,就可以使图中的黑色部分构成一个中心对称图形.
故答案为9.
12.中心
【解析】解:如果两个图形的对应点连成的线段都经过某一点,并且被这一点平分,则这两个图形一定关于这一点成中心对称.
故答案为:中心.
13.-8
2
【解析】略
14.
【解析】解:点A(-3,4)关于原点对称的点的坐标为:(3,-4)
故答案为:(3,-4)
15.4
【解析】如图所示,图形中的虚线是对称轴,所以对称轴有4条.
故答案为4.
16.CO;
DO
【解析】∵△ABO和△CDO关于点O成中心对称,
∴△ABO≌△CDO,
∴AO=CO,BO=DO,
故答案为:CO;DO.
17.见解析
【解析】解:如图,点O即为所求
18.见解析
【解析】解:对称中心为点O;
对应点分别是:A和D,B和E,C和F;
对应线段分别是:和,和,和;
对应角分别是:和,和,和.
19.见解析.
【解析】如图,连结、、、、.
、是以为对称轴的对称点,
是的垂直平分线.
,.
同理,,.
.
.
.
、、在同一直线上,且.
点、是以点为对称中心的对称点.
20.见解析
【解析】解:如图所示,分别作射线AO,BO,CO,再以O为圆心,分别以AO,BO,CO的长为半径画弧,分别交射线AO,BO,CO于A1,B1,C1,顺次连接A1,B1,C1,即为所求;
如图所示,分别作射线AO,BO,CO,再以O为圆心,分别以AO,BO,CO的长为半径画弧,分别交射线AO,BO,CO于A1,B1,C1,再以C1为圆心,以A1C1为半径画圆,连接A1C1,B1C1分别与圆交于E、D,即为所求
21.125.
【解析】解:∵(1+9)+(2+8)+(3+7)+(4+6)+…+(8+2)+(3+7)+(4+6)+(5+5)+(6+4)+5
=10×12+5
=120+5
=125
∴这组数和为125.
22.(1)图见详解;A1(1,-1),B1(3,-2),C1(4,1)
(2)图见详解;A2(3,-5),B2(5,-6),C2(6,-3)
【解析】(1)A(-1,1),B(-3,2),C(-4,-1)关于原点对称的点的坐标为A1(1,-1),B1(3,-2),C1(4,1),连接各点即可.如图:
(2)设A(-1,1),B(-3,2),C(-4,-1)关于P(1,-2)的对称点坐标为A2(a,m),B2(b,n),C2(c,s),则
,解得;,解得;
,解得;,解得;
,解得;,解得;
故A2(3,-5),B2(5,-6),C2(6,-3).
如图:
23.(1)见解析;(2),;(3),
【解析】(1)如图,为所作;
(2)∵点,点,
∴点,点.
(3)根据旋转的不变性,AB=A′B′,
∵∠A=∠A′,
∴AB∥A′B′.
24.(1)
直线AD、BE、CF以及线段AB、BC、CD的垂直平分线;(2)
60°或60°的整数倍;
(3)
或其整数倍.
【解析】(1)直线AD、BE、CF以及线段AB、BC、CD的垂直平分线都是这个正六边形的对称轴.
(2)因为正六边的中心角为60°,正六边形绕点O旋转60°或其整数倍后能和原来的图形重合.
(3)一般地,正n边形每条边的垂直平分线都是对称轴;
当n是偶数时,相对顶点的连线也是对称轴;
绕正n边形的中心旋转或其整数倍都能与原来的图形重合.
答案第1页,共2页
答案第1页,共2页
16.4中心对称图形-同步练习
时间:60分钟
一、单选题
1.下列图案中,是中心对称图形的是(
)
A.
B.
C.
D.
2.已知A、B两点关于原点对称,且A(3,4),则AB为( )
A.5
B.6
C.10
D.8
3.把图中阴影部分的小正方形移动一个,使它与其余四个阴影部分的正方形组成一个既是轴对称又是中心对称的新图形,这样的移法,正确的是( )
A.6→3
B.7→16
C.7→8
D.6→15
4.如图是一个中心对称图形,则此图形的对称中心为( )
A.A点
B.B点
C.C点
D.D点
5.如图,与关于成中心对称,不一定成立的结论是(
)
A.
B.
C.
D.
6.如图,四边形与四边形FGHE关于点O成中心对称,下列说法中错误的是(
)
A.
B.
C.
D.
7.如图,四边形ABCD与四边形FGHE关于一个点成中心对称,则这个点是( )
A.O1
B.O2
C.O3
D.O4
8.关于成中心对称的两个图形的性质,下列说法正确的是(
)
A.连接对应点的线段都经过对称中心,并且被对称中心平分
B.成中心对称的两个图形的对应线段不一定相等
C.对应点的连线不一定都经过对称中心
D.以上说法都不对
二、填空题
9.下列这些数字中有_____个是中心对称的图形.有_____个是轴对称的图形.
10.中心对称图形:如果一个图形绕着一个点旋转180°后,所得到的图形能够和原来的图形互相重合,那么这个图形叫做_____________,这个点叫_____________.
11.如图,是4×4正方形网格,把其中一个标有数字的白色小正方形涂黑,就可以使图中的黑色部分构成一个中心对称图形,则这个白色小正方形内的数字是_____.
12.如果两个图形的对应点连成的线段都经过某一点,并且被平分,则这两个图形一定关于这一点成____对称.
13.点
A(a,-2)与点
B(8,b)关于原点对称,则a
=___,b
=____.
14.点关于原点对称的点的坐标为______.
15.如图,请你画出方格纸中的图形关于点O的中心对称图形,整个图形的对称轴的条数为____条.
16.如图:△ABO与△CDO关于点O成中心对称,则AO=________,BO=_____.
三、解答题
17.图中的两个四边形关于某点对称,找出它们的对称中心.
18.如图,与关于点O成中心对称,请你写出两个三角形的对应点、对应线段、对应角和对称中心.
19.如图,,交点为,点、是以为对称轴的对称点,点、是以为对称轴的对称点,试说明点、是以点为对称中心的对称点.
20.分别画出下列图形关于点对称的图形.
21.有一组数排成方阵,如图所示,试计算这组数的和.小明想了想,方阵象正方形,正方形是轴对称图形,又是中心对称图形,能否利用轴对称和中心对称的思想来解决方阵的计算问题呢?小明试了试,竞得到了非常巧妙的方法,你能试试看吗?
1
2
3
4
5
2
3
4
5
6
3
4
5
6
7
4
5
6
7
8
5
6
7
8
9
22.已知:三点A(-1,1),B(-3,2),C(-4,-1).
(1)作出与△ABC关于原点对称的△A1B1C1,并写出各顶点的坐标;
(2)作出与△ABC关于P(1,-2)点对称的△A2B2C2,并写出各顶点的坐标.
23.如图,在平面直角坐标系中,点,点,将绕着点旋转180°后得到.
(1)在图中画出;
(2)求点、点的对称点和的坐标;
(3)请直接写出和的数量关系和位置关系.
24.如图,点O是正六边形ABCDEF的中心.
(1)找出这个轴对称图形的对称轴;
(2)这个正六边形绕点O旋转多少度后能和原来的图形重合?
(3)如果换成其他的正多边形呢?能得到一般的结论吗?
试卷第1页,共3页
参考答案
1.B
【解析】略
2.C
【解析】B两点关于原点对称,且A(3,4),那么B;根据两点的距离公式可得AB=10
故选:C.
3.D
【解析】解:6→3
,能使它与其余四个阴影部分的正方形组成一个轴对称图形,但不是中心对称图形
,故不符合题意;
B.
7→16,能使它与其余四个阴影部分的正方形组成一个中心对称图形,但不是轴对称图形,故不符合题意;
C.
7→8
,能使它与其余四个阴影部分的正方形组成一个轴对称图形,但不是中心对称图形,故不符合题意;
D.
6→15,能使它与其余四个阴影部分的正方形组成一个既是轴对称又是中心对称的新图形,故符合题意;
故选D.
4.B
【解析】解:如图所示:
点A与点C是对应点,点D与点E是对应点,线段AC与DE相交于点B,
所以点B是对称中心.
故选B.
5.D
【解析】解:对应点的连线被对称中心平分,A,B正确;
成中心对称图形的两个图形是全等形,那么对应线段相等,C正确;
和不是对应角,D错误.
故选:D.
6.D
【解析】A.∵与关于点O成中心对称,
∴,同理可得,正确;
B.∵点B与点G关于点O成中心对称,
∴,正确;
C.∵与关于点O成中心对称,
∴,同理可得,正确;
D.∵点D与点E关于点O成中心对称,
∴,
∴错误,
故选:D.
7.A
【解析】如图,连接HC和DE交于O1,
故选A.
8.A
【解析】根据中心对称的性质:
A.
连接对应点的线段都经过对称中心,并且被对称中心平分,此选项正确;
B.
根据成中心对称的两个图形的对应线段一定相等,故此选项错误;
C.
根据对应点的连线一定都经过对称中心,故此选项错误;
D.
以上说法都不对,此选项错误.
故答案选:A.
9.5
4
【解析】略
10.中心对称图形;
对称中心.
【解析】解:∵把一个图形绕着一个点旋转180°后,所得到的图形能够和原来的图形互相重合,那么这个图形叫做中心对称图形,这个点叫对称中心.
∴答案为:中心对称图形;对称中心.
11.9
【解析】如图,把标有数字9的白色小正方形涂黑,就可以使图中的黑色部分构成一个中心对称图形.
故答案为9.
12.中心
【解析】解:如果两个图形的对应点连成的线段都经过某一点,并且被这一点平分,则这两个图形一定关于这一点成中心对称.
故答案为:中心.
13.-8
2
【解析】略
14.
【解析】解:点A(-3,4)关于原点对称的点的坐标为:(3,-4)
故答案为:(3,-4)
15.4
【解析】如图所示,图形中的虚线是对称轴,所以对称轴有4条.
故答案为4.
16.CO;
DO
【解析】∵△ABO和△CDO关于点O成中心对称,
∴△ABO≌△CDO,
∴AO=CO,BO=DO,
故答案为:CO;DO.
17.见解析
【解析】解:如图,点O即为所求
18.见解析
【解析】解:对称中心为点O;
对应点分别是:A和D,B和E,C和F;
对应线段分别是:和,和,和;
对应角分别是:和,和,和.
19.见解析.
【解析】如图,连结、、、、.
、是以为对称轴的对称点,
是的垂直平分线.
,.
同理,,.
.
.
.
、、在同一直线上,且.
点、是以点为对称中心的对称点.
20.见解析
【解析】解:如图所示,分别作射线AO,BO,CO,再以O为圆心,分别以AO,BO,CO的长为半径画弧,分别交射线AO,BO,CO于A1,B1,C1,顺次连接A1,B1,C1,即为所求;
如图所示,分别作射线AO,BO,CO,再以O为圆心,分别以AO,BO,CO的长为半径画弧,分别交射线AO,BO,CO于A1,B1,C1,再以C1为圆心,以A1C1为半径画圆,连接A1C1,B1C1分别与圆交于E、D,即为所求
21.125.
【解析】解:∵(1+9)+(2+8)+(3+7)+(4+6)+…+(8+2)+(3+7)+(4+6)+(5+5)+(6+4)+5
=10×12+5
=120+5
=125
∴这组数和为125.
22.(1)图见详解;A1(1,-1),B1(3,-2),C1(4,1)
(2)图见详解;A2(3,-5),B2(5,-6),C2(6,-3)
【解析】(1)A(-1,1),B(-3,2),C(-4,-1)关于原点对称的点的坐标为A1(1,-1),B1(3,-2),C1(4,1),连接各点即可.如图:
(2)设A(-1,1),B(-3,2),C(-4,-1)关于P(1,-2)的对称点坐标为A2(a,m),B2(b,n),C2(c,s),则
,解得;,解得;
,解得;,解得;
,解得;,解得;
故A2(3,-5),B2(5,-6),C2(6,-3).
如图:
23.(1)见解析;(2),;(3),
【解析】(1)如图,为所作;
(2)∵点,点,
∴点,点.
(3)根据旋转的不变性,AB=A′B′,
∵∠A=∠A′,
∴AB∥A′B′.
24.(1)
直线AD、BE、CF以及线段AB、BC、CD的垂直平分线;(2)
60°或60°的整数倍;
(3)
或其整数倍.
【解析】(1)直线AD、BE、CF以及线段AB、BC、CD的垂直平分线都是这个正六边形的对称轴.
(2)因为正六边的中心角为60°,正六边形绕点O旋转60°或其整数倍后能和原来的图形重合.
(3)一般地,正n边形每条边的垂直平分线都是对称轴;
当n是偶数时,相对顶点的连线也是对称轴;
绕正n边形的中心旋转或其整数倍都能与原来的图形重合.
答案第1页,共2页
答案第1页,共2页
同课章节目录
- 第十二章 分式和分式方程
- 12.1 分式
- 12.2 分式的乘除
- 12.3 分式的加减
- 12.4 分式方程
- 12.5 分式方程的应用
- 第十三章 全等三角形
- 13.1 命题与证明
- 13.2 全等图形
- 13.3 全等三角形的判定
- 13.4 三角形的尺规作图
- 第十四章 实数
- 14.1 平方根
- 14.2 立方根
- 14.3 实数
- 14.4 近似数
- 14.5 用计算器求平方根与立方根
- 第十五章 二次根式
- 15.1 二次根式
- 15.2 二次根式的乘除
- 15.3 二次根式的加减
- 15.4 二次根式的混合
- 第十六章 轴对称和中心对称
- 16.1 轴对称
- 16.2 线段的垂直平分
- 16.3 角的平分线
- 16.4 中心对称图形
- 16.5 利用图形的平移、旋转和轴对称设计图案
- 第十七章 特殊三角形
- 17.1 等腰三角形
- 17.2 直角三角形
- 17.3 勾股定理
- 17.4 直角三角形全等的判定
- 17.5 反证法
