2021--2022学年沪科版七年级数学上册_2.1 代数式 课件(共21张PPT)
文档属性
| 名称 | 2021--2022学年沪科版七年级数学上册_2.1 代数式 课件(共21张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 544.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-05 08:06:03 | ||
图片预览







文档简介
(共21张PPT)
第五课时
求代数式的值
沪科版七年级数学(上)
第二章
整式的加减
§2.1
代
数
式
次数:所有字母的指数的和。
系数:单项式中的数字因数。
项:式中的每个单项式叫多项式的项。
(其中不含字母的项叫做常数项)
次数:多项式中次数最高的项的次数。
整式
知识回顾
(1)单独一个数或一个字母也是单项式;常数的次数为0
,
(2)单项式的系数包括它前面的符号,多项式的每一项都包括它前面的符号,都有正号也有负号.
(3)单项式的次数是所有字母的指数的和;多项式的次数不是所有项的和.
数字母积的形式
单项式和的形式
练一练
(1)4×102a2b的次数是(
),系数是(
)
3
4×102
(2)多项式3x2y-xy2+x3y3-x4y4-1是(
)次(
)项式,按字母y的降幂排列是(
)
八
五
-x4y4+x3y3-xy2+3x2y-1
(3)
下列说法错误的是( )
A.m是单项式也是整式
B.
是多项式也是整式
C.整式一定是单项式
D.整式不一定是多项式
C
(4)如果多项式xn-2-5x+2是关于x的三次三项式,那么n等于( )
A.3
B.4
C.5
D.6
C
新课导入
据报载,一位医生研究得出有父母身高预测子女身高的公式:若父亲的身高为a米,母亲的身高是b米,则儿子成年的身高为
米,
女儿成年的身高为
米
七年级男生张晓华的父亲身高1.76米,母亲身高为1.60米,你能预测张晓华成年后的身高吗?
活动一
活动二
你能通过你父母的身高预测你自己成年后的身高吗?
求代数式的值
新课讲解
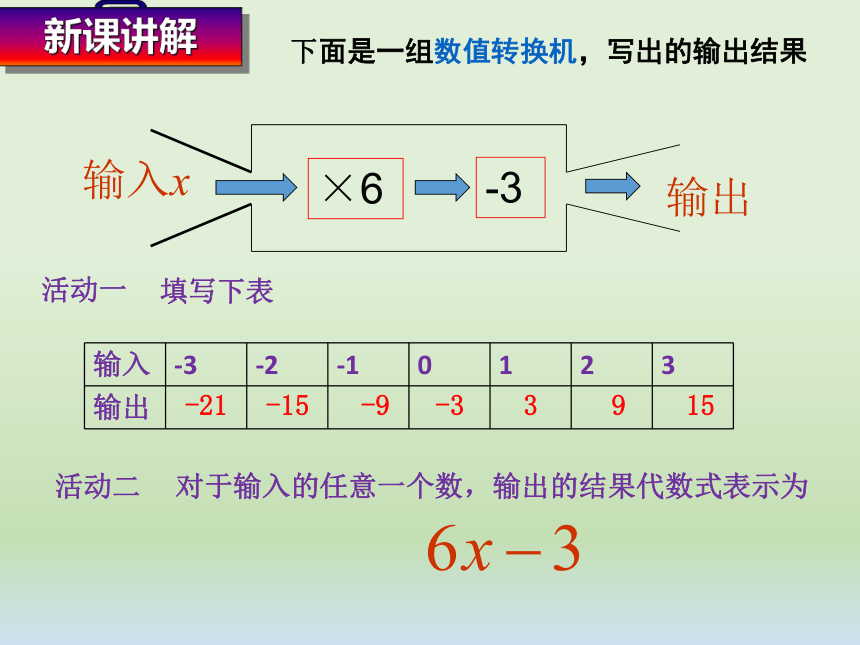
下面是一组数值转换机,写出的输出结果
×6
-3
输入
-3
-2
-1
0
1
2
3
输出
-21
-15
-9
-3
3
9
15
活动一
填写下表
活动二
对于输入的任意一个数,输出的结果代数式表示为
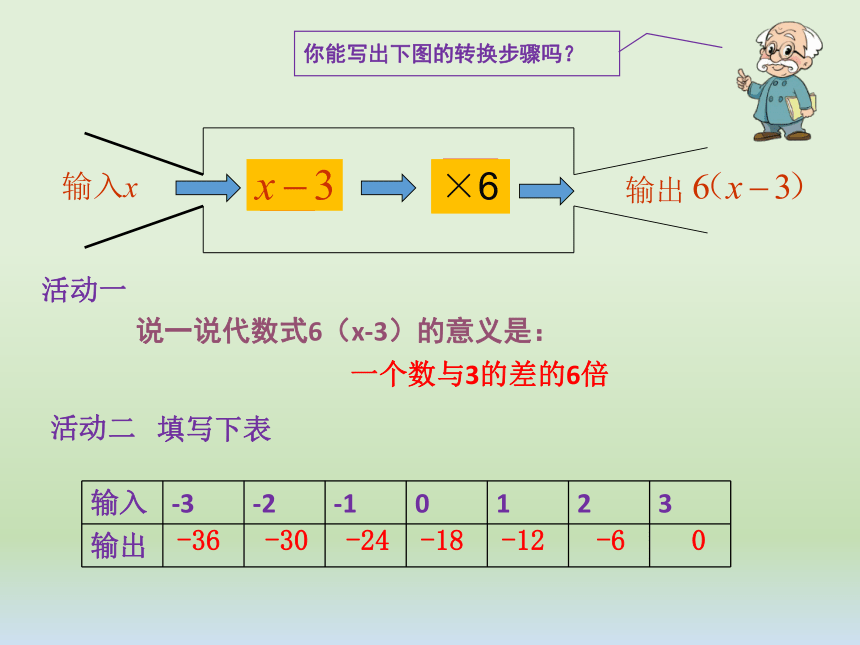
你能写出下图的转换步骤吗?
×6
说一说代数式6(x-3)的意义是:
一个数与3的差的6倍
输入
-3
-2
-1
0
1
2
3
输出
填写下表
活动一
活动二
-36
-24
-18
-12
-6
0
-30
一般的,用数值代替代数式里的字母,计算后所得的结果叫做代数式的值。
定义
代数式的值
求代数式的值的一般步骤:
1.写明字母所取的值,即“当……时”;
2.写明所要求值的代数式;
3.将字母所取的值代入该代数式中的相同字母中,根据运算关系求出计算结果.
新课讲解
例题精讲
代数式省略的乘号,代入时注意加上
例2
(1)当
解:
例题精讲
字母的值是分数,代入时注意加括号
(2)当
解:
字母的值是负数,代入时注意加括号
例题精讲
(2)当
解:
你做对了吗
例题精讲
1、如果字母的值是分数,并且要计算它的平方、立方,代入时也应将分数加上括号;
3、用直接代入法求含字母的式子的值可以分三步:
(1)“当……时”,即指出字母的值;
(2)“原式=……”,即代入所给字母的值;
(3)计算.
求代数式的值需要注意什么
2、代数式中省略了乘号时,代入数值以后必须添上乘号。
例3、按下图方式摆放餐桌和椅子:
(1)1张餐桌可坐6人,2张餐桌可
人.
(2)按照上图的方式继续排列餐桌,完成下表:
桌子张数
3
4
5
6
……
可坐人数
4+4
+4+2
4+4+4+4+2
4+4+4+4+4+2
4+4+4+4+4+4+2
4+4+2
……
(3)探索餐桌张数n与可坐人数w之间的关系.
w=4n+2
(4)15张餐桌这样排,可坐多少人?
解:当n=15时,w=4×15+2=62
新知应用
10
若按下图方式将桌子拼在一起:
(1)2张桌子拼在一起可坐
人,
3张桌子可坐
人,
n张桌子可坐 人;
(2)一家餐厅有40张这样的长方形桌子,按照上图方式每5张拼成1张大桌子,则40张桌子可拼成8张大桌子,共可坐
人;
(3)在(2)中,若改成每8张桌子拼成1张大桌子,则共可坐
人.
2×2+4
2n+4
112
100
2×3+4
新知应用
1、填图:
n
3n2-2n+4
3
0
-4
课后练习
2、如图是一个圆环,外圆与内圆的半径分别是R和r.
(1)用代数式表示圆环面积.
(2)当R=5cm,r=2cm时,圆环的面积是多少(π取3.14)?
解:圆环面积=大圆面积-小圆面积.
解:将R=5cm,r=2cm带入上式
答:圆环的面积是65.94平方厘米.
3、设甲数是x,乙数是y.
(1)用代数式表示甲,乙两数和的立方;
(2)用代数式表示甲,乙两数的立方和;
(3)当x=-2,y=-1时,计算(1)和(2)所列代数式的值;
能力提升
1、某商店出售一批水果,最初以每箱a元的价格出售m箱,后来每箱降价为b元,又售出m箱,剩下30箱又以每箱再降价5元出售.
(1)用代数式表示这批水果共售多少元?
(2)如果a=20,b=18,m=60,进这批水果共花去1500元,那么该商店赚了多少元?
解:(1)[am+bm+30(b-5)]元
(2)
当a=20,b=18,m=60
am+bm+30(b-5)
=20
×60+18
×60+30
×(18-5)
=2670(元)
2670
-1500=1170(元)
答:该商店赚了1170元
2、数学课上,李老师编制了一个程序,当输入任意一个有理数时,显示屏上的结果总是为输入的有理数的平方与1的差的2倍,若输入-1,并将显示的结果再次输入,则这时显示的结果是多少.
解:设输入的有理数是x
编制的程序所代表的代数式为:2(x2-1),
当x=-1时,2(x2-1)=0
把x=0代入,
2(x2-1)=2(0-1)=
-2
答:显示的结果是-2
1.
若a-b=
-2,那么(a-b)2的值是
,
3a-3b+5的值是
2.若代数式2x2+3x+7的值是8,则代数式4x2+6x+15的值是_______
拓展练习
3.堤坝的横截面是一个梯形,如图,测得梯形
的上底a=18米,下底b=36米,高h=20米,求这个横截面的面积
a=18
b=36
h=20
1、代数式的值:用数代替代数式里的字母,计算后所得结果叫做
。
代数式的值
2、代数式求值步骤
(1)代入
(2)计算
课堂小结
3、代数式求值注意事项
(1)格式规范
(2)适当添加括号
(3)灵活运用整体代入
第五课时
求代数式的值
沪科版七年级数学(上)
第二章
整式的加减
§2.1
代
数
式
次数:所有字母的指数的和。
系数:单项式中的数字因数。
项:式中的每个单项式叫多项式的项。
(其中不含字母的项叫做常数项)
次数:多项式中次数最高的项的次数。
整式
知识回顾
(1)单独一个数或一个字母也是单项式;常数的次数为0
,
(2)单项式的系数包括它前面的符号,多项式的每一项都包括它前面的符号,都有正号也有负号.
(3)单项式的次数是所有字母的指数的和;多项式的次数不是所有项的和.
数字母积的形式
单项式和的形式
练一练
(1)4×102a2b的次数是(
),系数是(
)
3
4×102
(2)多项式3x2y-xy2+x3y3-x4y4-1是(
)次(
)项式,按字母y的降幂排列是(
)
八
五
-x4y4+x3y3-xy2+3x2y-1
(3)
下列说法错误的是( )
A.m是单项式也是整式
B.
是多项式也是整式
C.整式一定是单项式
D.整式不一定是多项式
C
(4)如果多项式xn-2-5x+2是关于x的三次三项式,那么n等于( )
A.3
B.4
C.5
D.6
C
新课导入
据报载,一位医生研究得出有父母身高预测子女身高的公式:若父亲的身高为a米,母亲的身高是b米,则儿子成年的身高为
米,
女儿成年的身高为
米
七年级男生张晓华的父亲身高1.76米,母亲身高为1.60米,你能预测张晓华成年后的身高吗?
活动一
活动二
你能通过你父母的身高预测你自己成年后的身高吗?
求代数式的值
新课讲解
下面是一组数值转换机,写出的输出结果
×6
-3
输入
-3
-2
-1
0
1
2
3
输出
-21
-15
-9
-3
3
9
15
活动一
填写下表
活动二
对于输入的任意一个数,输出的结果代数式表示为
你能写出下图的转换步骤吗?
×6
说一说代数式6(x-3)的意义是:
一个数与3的差的6倍
输入
-3
-2
-1
0
1
2
3
输出
填写下表
活动一
活动二
-36
-24
-18
-12
-6
0
-30
一般的,用数值代替代数式里的字母,计算后所得的结果叫做代数式的值。
定义
代数式的值
求代数式的值的一般步骤:
1.写明字母所取的值,即“当……时”;
2.写明所要求值的代数式;
3.将字母所取的值代入该代数式中的相同字母中,根据运算关系求出计算结果.
新课讲解
例题精讲
代数式省略的乘号,代入时注意加上
例2
(1)当
解:
例题精讲
字母的值是分数,代入时注意加括号
(2)当
解:
字母的值是负数,代入时注意加括号
例题精讲
(2)当
解:
你做对了吗
例题精讲
1、如果字母的值是分数,并且要计算它的平方、立方,代入时也应将分数加上括号;
3、用直接代入法求含字母的式子的值可以分三步:
(1)“当……时”,即指出字母的值;
(2)“原式=……”,即代入所给字母的值;
(3)计算.
求代数式的值需要注意什么
2、代数式中省略了乘号时,代入数值以后必须添上乘号。
例3、按下图方式摆放餐桌和椅子:
(1)1张餐桌可坐6人,2张餐桌可
人.
(2)按照上图的方式继续排列餐桌,完成下表:
桌子张数
3
4
5
6
……
可坐人数
4+4
+4+2
4+4+4+4+2
4+4+4+4+4+2
4+4+4+4+4+4+2
4+4+2
……
(3)探索餐桌张数n与可坐人数w之间的关系.
w=4n+2
(4)15张餐桌这样排,可坐多少人?
解:当n=15时,w=4×15+2=62
新知应用
10
若按下图方式将桌子拼在一起:
(1)2张桌子拼在一起可坐
人,
3张桌子可坐
人,
n张桌子可坐 人;
(2)一家餐厅有40张这样的长方形桌子,按照上图方式每5张拼成1张大桌子,则40张桌子可拼成8张大桌子,共可坐
人;
(3)在(2)中,若改成每8张桌子拼成1张大桌子,则共可坐
人.
2×2+4
2n+4
112
100
2×3+4
新知应用
1、填图:
n
3n2-2n+4
3
0
-4
课后练习
2、如图是一个圆环,外圆与内圆的半径分别是R和r.
(1)用代数式表示圆环面积.
(2)当R=5cm,r=2cm时,圆环的面积是多少(π取3.14)?
解:圆环面积=大圆面积-小圆面积.
解:将R=5cm,r=2cm带入上式
答:圆环的面积是65.94平方厘米.
3、设甲数是x,乙数是y.
(1)用代数式表示甲,乙两数和的立方;
(2)用代数式表示甲,乙两数的立方和;
(3)当x=-2,y=-1时,计算(1)和(2)所列代数式的值;
能力提升
1、某商店出售一批水果,最初以每箱a元的价格出售m箱,后来每箱降价为b元,又售出m箱,剩下30箱又以每箱再降价5元出售.
(1)用代数式表示这批水果共售多少元?
(2)如果a=20,b=18,m=60,进这批水果共花去1500元,那么该商店赚了多少元?
解:(1)[am+bm+30(b-5)]元
(2)
当a=20,b=18,m=60
am+bm+30(b-5)
=20
×60+18
×60+30
×(18-5)
=2670(元)
2670
-1500=1170(元)
答:该商店赚了1170元
2、数学课上,李老师编制了一个程序,当输入任意一个有理数时,显示屏上的结果总是为输入的有理数的平方与1的差的2倍,若输入-1,并将显示的结果再次输入,则这时显示的结果是多少.
解:设输入的有理数是x
编制的程序所代表的代数式为:2(x2-1),
当x=-1时,2(x2-1)=0
把x=0代入,
2(x2-1)=2(0-1)=
-2
答:显示的结果是-2
1.
若a-b=
-2,那么(a-b)2的值是
,
3a-3b+5的值是
2.若代数式2x2+3x+7的值是8,则代数式4x2+6x+15的值是_______
拓展练习
3.堤坝的横截面是一个梯形,如图,测得梯形
的上底a=18米,下底b=36米,高h=20米,求这个横截面的面积
a=18
b=36
h=20
1、代数式的值:用数代替代数式里的字母,计算后所得结果叫做
。
代数式的值
2、代数式求值步骤
(1)代入
(2)计算
课堂小结
3、代数式求值注意事项
(1)格式规范
(2)适当添加括号
(3)灵活运用整体代入
同课章节目录
- 第1章 有理数
- 1.1 正数和负数
- 1.2 数轴、相反数和绝对值
- 1.3 有理数的大小
- 1.4 有理数的加减
- 1.5 有理数的乘除
- 1.6 有理数的乘方
- 1.7 近似数
- 第2章 整式加减
- 2.1 代数式
- 2.2 整式加减
- 第3章 一次方程与方程组
- 3.1 一元一次方程及其解法
- 3.2 一元一次方程的应用
- 3.3二元一次方程组及其解法
- 3.4 二元一次方程组的应用
- 3.5 三元一次方程组及其解法
- 第4章 直线与角
- 4.1 几何图形
- 4.2 线段、射线、直线
- 4.3 线段的 长短比较
- 4.4 角
- 4.5 角的比较与补(余)角
- 4.6 用尺规作线段与角
- 第5章 数据的收集与整理
- 5.1 数据的 收集
- 5.2 数据的整理
- 5.3 用统计图描述数据
- 5.4 从图表中的数据获取信息
