2.5三角函数的应用 同步能力达标测评 2021-2022学年鲁教版(五四制)九年级数学上册(word版含答案)
文档属性
| 名称 | 2.5三角函数的应用 同步能力达标测评 2021-2022学年鲁教版(五四制)九年级数学上册(word版含答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 661.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-05 08:27:33 | ||
图片预览




文档简介
2021-2022学年鲁教版九年级数学上册《2.5三角函数的应用》同步能力提升训练(附答案)
一、选择题
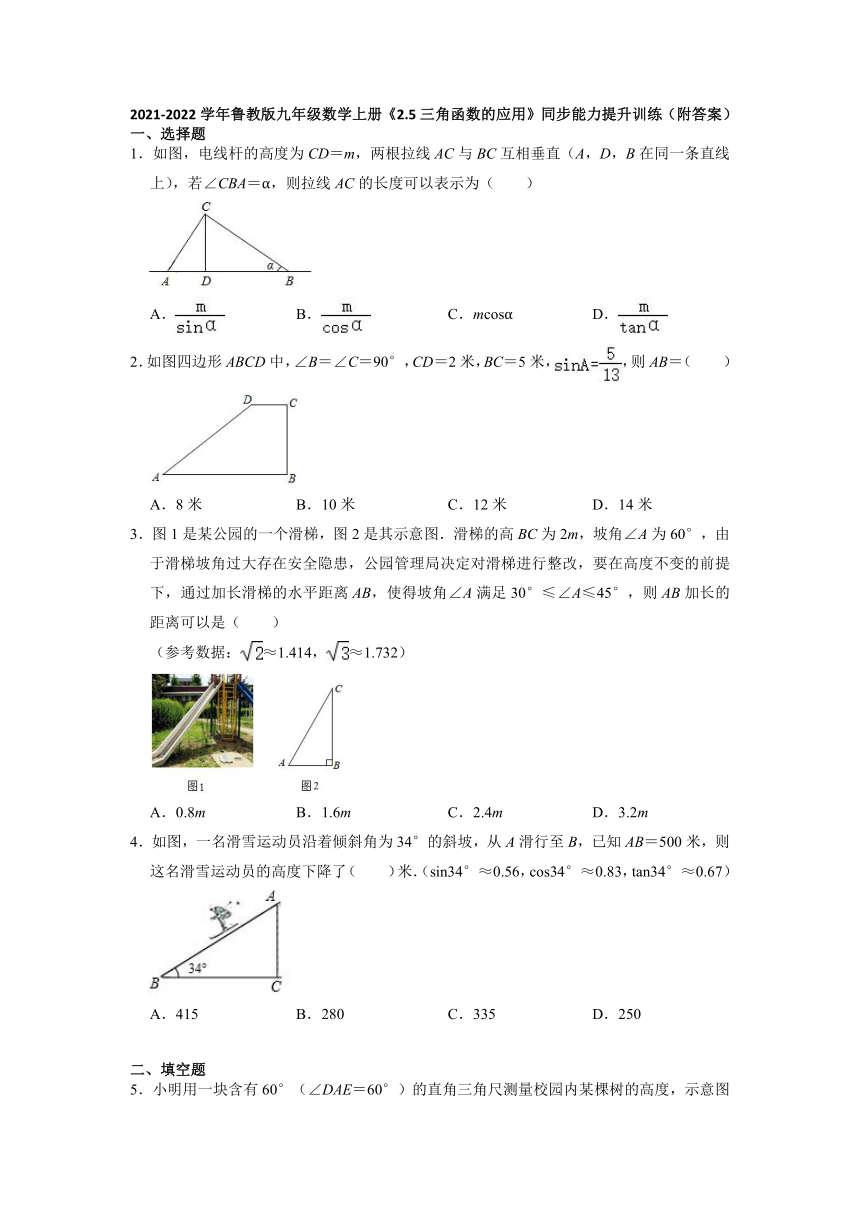
1.如图,电线杆的高度为CD=m,两根拉线AC与BC互相垂直(A,D,B在同一条直线上),若∠CBA=α,则拉线AC的长度可以表示为( )
A.
B.
C.mcosα
D.
2.如图四边形ABCD中,∠B=∠C=90°,CD=2米,BC=5米,,则AB=( )
A.8米
B.10米
C.12米
D.14米
3.图1是某公园的一个滑梯,图2是其示意图.滑梯的高BC为2m,坡角∠A为60°,由于滑梯坡角过大存在安全隐患,公园管理局决定对滑梯进行整改,要在高度不变的前提下,通过加长滑梯的水平距离AB,使得坡角∠A满足30°≤∠A≤45°,则AB加长的距离可以是( )
(参考数据:≈1.414,≈1.732)
A.0.8m
B.1.6m
C.2.4m
D.3.2m
4.如图,一名滑雪运动员沿着倾斜角为34°的斜坡,从A滑行至B,已知AB=500米,则这名滑雪运动员的高度下降了( )米.(sin34°≈0.56,cos34°≈0.83,tan34°≈0.67)
A.415
B.280
C.335
D.250
二、填空题
5.小明用一块含有60°(∠DAE=60°)的直角三角尺测量校园内某棵树的高度,示意图如图所示,若小明的眼睛与地面之间的垂直高度AB为1.62m,小明与树之间的水平距离BC为4m,则这棵树的高度约为
m.(结果精确到0.1m,参考数据:≈1.73)
6.如图,地面上两个村庄C、D处于同一水平线上,一飞行器在空中以12千米/小时的速度沿MN方向水平飞行,航线MN与C、D在同一铅直平面内.当该飞行器飞至村庄C的正上方A处时,测得∠NAD=60°,该飞行器从A处飞行40分钟至B处时,测得∠ABD=75°,则村庄C、D间的距离为
千米.(≈1.732,结果保留一位小数)
7.如图,同学们利用所学知识去测量三江源某河段某处的宽度,小明同学在A处观测对岸点C.测得∠CAD=45°,小刚同学在距点A处60米远的B点测得∠CBD=30°,根据这些数据可以算出河宽为
米(精确到0.01米,≈1.414,≈1.732).
8.如图,一架长为10米的梯子AB斜靠在一竖直的墙AO上,这时测得∠ABO=70°,如果梯子的底端B外移到D,则梯子顶端A下移到C,这时又测得∠CDO=50°,那么AC的长度约为
米.(sin70°≈0.94,sin50°≈0.77,cos70°≈0.34,cos50°≈0.64)
9.某型号飞机的机翼形状如图所示,根据图中数据计算AB的长度为
.(结果保留小数点后两位,≈1.732)
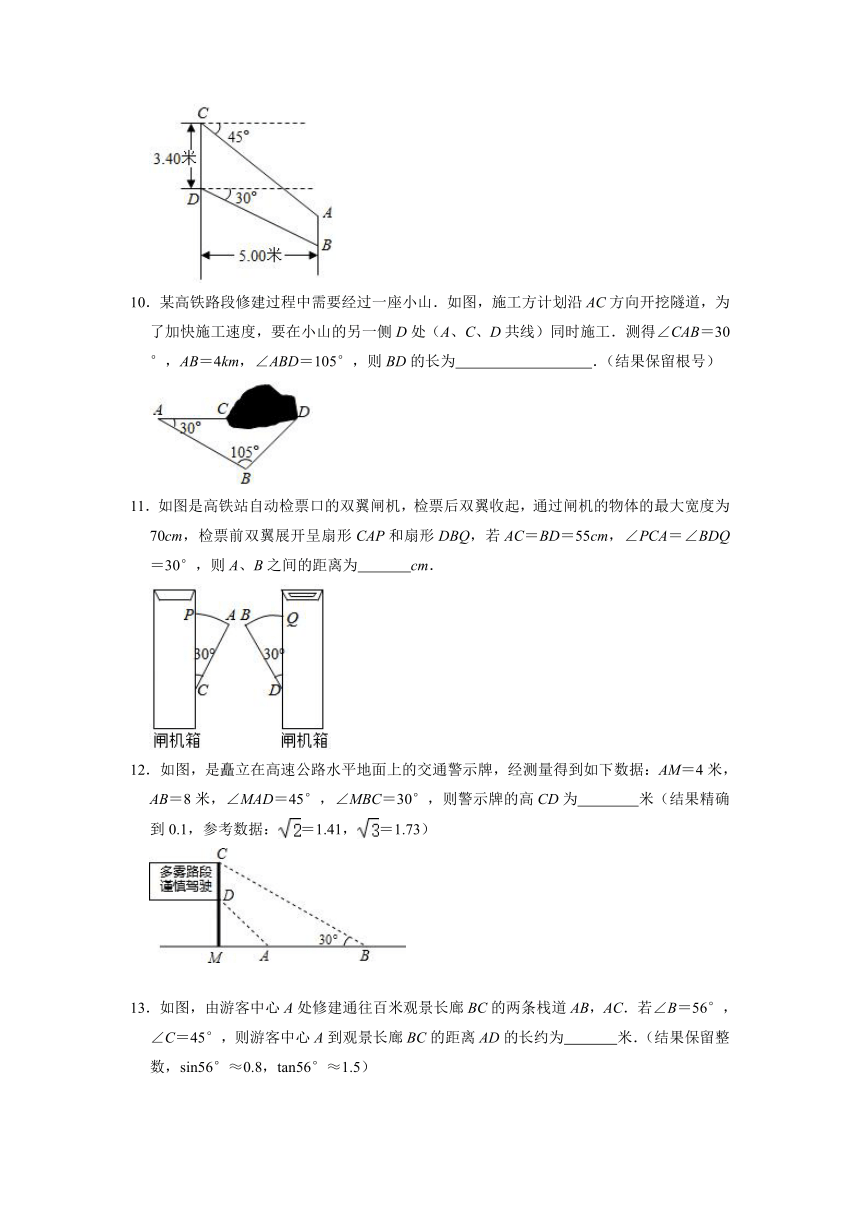
10.某高铁路段修建过程中需要经过一座小山.如图,施工方计划沿AC方向开挖隧道,为了加快施工速度,要在小山的另一侧D处(A、C、D共线)同时施工.测得∠CAB=30°,AB=4km,∠ABD=105°,则BD的长为
.(结果保留根号)
11.如图是高铁站自动检票口的双翼闸机,检票后双翼收起,通过闸机的物体的最大宽度为70cm,检票前双翼展开呈扇形CAP和扇形DBQ,若AC=BD=55cm,∠PCA=∠BDQ=30°,则A、B之间的距离为
cm.
12.如图,是矗立在高速公路水平地面上的交通警示牌,经测量得到如下数据:AM=4米,AB=8米,∠MAD=45°,∠MBC=30°,则警示牌的高CD为
米(结果精确到0.1,参考数据:=1.41,=1.73)
13.如图,由游客中心A处修建通往百米观景长廊BC的两条栈道AB,AC.若∠B=56°,∠C=45°,则游客中心A到观景长廊BC的距离AD的长约为
米.(结果保留整数,sin56°≈0.8,tan56°≈1.5)
14.如图,某商场大厅自动扶梯AB的长为12m,它与水平面AC的夹角∠BAC=30°,则大厅两层之间的高度BC为
m.
15.如图,某水库水坝的坝高为24米,如果迎水坡AB的坡度为1:0.75,那么该水库迎水坡AB的长度为
米.
16.如图,我市在建高铁的某段路基横断面为梯形ABCD,DC∥AB.BC长6米,坡角β为45°,AD的坡角α为30°,则AD长为
米(结果保留根号).
三、解答题
17.如图(1)是一种简易台灯,在其结构图(2)中灯座为△ABC(BC伸出部分不计),A、C、D在同一直线上.量得∠ACB=90°,∠A=60°,AB=16cm,∠ADE=135°,灯杆CD长为40cm,灯管DE长为15cm.
(1)求DE与水平桌面(AB所在直线)所成的角;
(2)求台灯的高(点E到桌面的距离,结果精确到0.1cm).
(参考数据:sin15°=0.26,cos15°=0.97,tan15°=0.27,sin30°=0.5,cos30°=0.87,tan30°=0.58.)
18.如图,有一电线杆AB直立于地面,它的影子正好射在地面BC段和与地面成45°角的土坡CD上,已知∠BAD=60°,BC=8米,CD=2米,求电线杆AB的高.(结果保留3个有效数字,≈1.732)
19.如图,河流的两岸PQ、MN互相平行,河岸PQ上有一排小树,已知相邻两树之间的距离CD=50米,某人在河岸MN的A处测的∠DAN=35°,然后沿河岸走了130米到达B处,测的∠CBN=60°,求河流的宽度CE(结果保留整数).
(参考数据:sin35°≈0.6,cos35°≈0.8,tan35°≈0.7,≈1.7)
20.超速行驶是引发交通事故的主要原因.上周末,小明和三位同学尝试用自己所学的知识检测车速,如图,观测点设在到永丰路的距离为100米的点P处.这时,一辆小轿车由西向东匀速行驶,测得此车从A处行驶到B处所用的时间为4秒,∠APO=60°,∠BPO=45°.
(1)求A、B之间的路程;
(2)请判断此车是否超过了永丰路每小时54千米的限制速度?(参考数据:≈1.73)
21.小明同学想测量位于池塘两端的A、B两点的距离.他沿着与直线AB平行的道路EF行走,当行走到点C处,测得∠ACF=45°,再向前行走一段距离时到点D处,侧得∠BDF=65°.若直线AB与EF之间的距离为60米.
(1)设池塘两端的距离AB=x米,试用含x的代数式表示CD的长;
(2)当CD=100米时,求A、B两点的距离(计算结果精确到个位).(参考数据:sin45°≈0.71,cos65°≈0.42,tan65°≈2.14.)
22.“低碳生活,绿色出行”,自行车正逐渐成为人们喜爱的交通工具,如图1所示是一辆自行车的实物图,车架档AC与CD的长分别为45cm,60cm,且它们互相垂直,座杆CE的长为20cm,点A,C,E在同一条直线上,且∠CAB=75°,如图2.
(1)求车架档AD的长;
(2)求车座点E到车架档AB的距离(结果精确到1cm,参考数据sin75°=0.966,cos75°=0.259,tan75°=3.732)
23.图①是一种手机平板支架,由托板、支撑板和底座构成,手机放置在托板上,图②是其侧面结构示意图,托板长AB=115mm,支撑板长CD=70mm,板AB固定在支撑板顶点C处,且CB=35mm,托板AB可绕点C转动,支撑板CD可绕点D转动,∠CDE=60°.
(1)若∠DCB=70°时,求点A到直线DE的距离(计算结果精确到个位);
(2)为了观看舒适,把(1)中∠DCB=70°调整为90°,再将CD绕点D逆时针旋转,使点B落在直线DE上即可,求CD旋转的角度.
(参考数据:sin50°≈0.8,cos50°≈0.6,tan50°≈1.2,sin26.6°≈0.4,cos26.6°≈0.9,tan26.6°≈0.5,≈1.7)
24.已知,图1是一辆登高云梯消防车的实物图,图2是其工作示意图,起重臂AC可伸缩(10m≤AC≤20m),且起重臂AC可绕点A在一定范围内转动,张角为∠CAE(90°≤∠CAE≤150°),转动点A距离地面BD的高度AE为3.5m.
(1)当起重臂AC长度为12m,张角∠CAE为120°时,求云梯消防车最高点C距离地面的高;
(2)某日,一居民家突发险情,该居民家距离地面的高度为20m,请问该消防车能否实施有效救援?(参考数据:≈1.732)
25.小慧要外出参加活动,需网购拉杆箱,图①,图②分别是她在网上看到的某型号拉杆箱实物图与示意图,并获得如下信息:滑杆DE、箱长BC、拉杆AB的长度相等,B、F在AC上,C在DE上,支杆DF=30cm,CE:CD=1:3,∠DCF=45°,∠CDF=30°,请根据以上信息,解决下列问题:
(1)求AC的长度(结果保留根号);
(2)求拉杆端点A到水平滑杆ED的距离(结果保留根号).
26.如图1,2分别是某款篮球架的实物图与示意图,已知支架AB与支架AC所成的角∠BAC=15°,点A、H、F在同一条直线上,支架AH段的长为1米,HF段的长为1.50米,篮板底部水平支架HE的长为0.75米,篮板顶端F到地面的距离为4.4米.
(1)求篮板底部支架HE与支架AF所成的角∠FHE的度数.
(2)求底座BC的长.(结果精确到0.1米;参考数据:sin15°≈0.26,cos15°≈0.97,tan15°=0.27,≈1.732,≈1.414)
参考答案
1.解:∵∠ACD+∠BCD=90°,∠CBD+∠BCD=90°,
∴∠ACD=∠CBD,
在Rt△ACD中,∵cos∠ACD=,
∴AC=,
故选:B.
2.解:过D作DE⊥AB于E,
∴∠DEB=∠B=∠C=90°,
∴四边形DEBC是矩形,
∴BE=DC=2米,DE=BC=5米,
∵sinA=,
∴,
∴AD=13(米),
∴AE=(米),
∴AB=AE+BE=12+2=14(米),
故选:D.
3.解:如图,在Rt△ABC,∠CAB=60°,BC=2m,
∴AB===,
当坡角为45°时,有BD=BC=2m,
∴DA=2﹣AB=2﹣≈0.85(m),
当坡角为30°时,有BE===2(m),
∴EA=BE﹣AB=2﹣≈2.31(m),
当坡角满足30°≤∠A≤45°,
∴AB加长的距离x的取值范围为0.85≤x≤2.31m,
故选:B.
4.解:在Rt△ABC中,∠ABC=34°,sin∠ABC=,
∴AC=AB sin34°≈500×0.56≈280(米),
∴这名滑雪运动员的高度下降了280米,
故选:B.
5.解:∵AB⊥BC,DC⊥BC,AD∥BC,
∴四边形ABCD是矩形,
∵BC=4m,AB=1.62m,
∴AD=BC=4m,DC=AB=1.62m,
Rt△AED中,∵∠DAE=60°,AD=4m,
∴ED=AD tan60°=4×=4(m),
∴CE=ED+DC=4+1.62≈8.5(m)
答:这棵树的高度约为8.5m.
故答案为:8.5.
6.解:如图,过B作BE⊥AD于E,
∵∠NAD=60°,∠ABD=75°,
∴∠ADB=45°,
∵AB=12×=8(千米),
∴AE=4(千米).BE=4(千米),
∴DE=BE=4(千米),
∴AD=(4+4)(千米),
∵∠C=90,∠CAD=30°,
∴CD=AD=2+2≈5.5(千米).
故答案为:5.5.
7.解:过C作CE⊥AB于E,设CE=x米,
在Rt△AEC中,∠CAE=45°,
∴AE=CE=x米,
在Rt△BCE中,∠CBE=30°,
∴BE=CE=x(米),
∴x=x+60,
解得,x=30+30≈81.96(米).
答:河宽约为81.96米.
故答案为:81.96.
8.解:由题意可得:
∵∠ABO=70°,AB=10m,
∴sin70°=,
解得:AO=9.4(m),
∵∠CDO=50°,DC=10m,
∴sin50°=≈0.77,
解得:CO=7.7(m),
则AC=9.4﹣7.7=1.70(m),
答:AC的长度约为1.70米.
故答案为:1.70.
9.解:如图,
在Rt△CEA中,∵cos∠ECA=,
∴CA=≈7.07(m);
在Rt△BDF中,∵cos∠BDF=,
∴DB=≈5.77(m),
∴BF=BD≈2.89(m),
∵AB+AE=EF+BF,
∴AB=3.4+2.89﹣5=1.29(m).
故答案为:1.29m.
10.解:过B作BE⊥AD于点E,
∵∠CAB=30°,AB=4km,
∴∠ABE=60°,BE=2km,
∵∠ABD=105°,
∴∠EBD=45°,
∴∠EDB=45°,
∴BE=DE=2km,
∴BD===2(km),
即BD的长是2km.
11.解:如图,连接AB,CD,过点A作AE⊥CD于E,过点B作BF⊥CD于F.
则CD=70cm,四边形AEFB是矩形,
∴EF=AB,
∵AE∥PC,
∴∠PCA=∠CAE=30°,
∴CE=AC sin30°=55×=(cm),
同理可得DF=(cm),
∴AB=EF=CD﹣CE﹣DF=70﹣﹣=15(cm),
故答案为:15.
12.解:由题意可得:∵AM=4米,∠MAD=45°,
∴DM=4m,
∵AM=4米,AB=8米,
∴MB=12米,
∵∠MBC=30°,
∴BC=2MC,
∴MC2+MB2=(2MC)2,
MC2+122=(2MC)2,
∴MC=4,
则DC=4﹣4≈2.9(米),
故答案为:2.9.
13.解:∵∠B=56°,∠C=45°,∠ADB=∠ADC=90°,BC=BD+CD=100米,
∴BD=,CD=,
∴+=100,
解得AD≈60.
故答案为:60.
14.解;在Rt△ABC中,∠BAC=30°,AB=12m,
∴BC=m,
故答案为:6.
15.解:如图,过点B作BC垂直于水平面于点C,
∵迎水坡AB的坡度为1:0.75
∴BC:AC=1:0.75,
∴24:AC=1:0.75,
∴AC=18(米),
∴AB=
==30(米),
即该大坝迎水坡AB的长度为30米,
故答案为:30.
16.解:过点D作DE⊥AB于E,过点C作CF⊥AB于F.
∵CD∥AB,DE⊥AB,CF⊥AB,
∴DE=CF,
在Rt△CFB中,CF=BC sin45°=3(米),
∴DE=CF=3(米),
在Rt△ADE中,∵∠A=30°,∠AED=90°,
∴AD=2DE=6(米),
故答案为:6.
17.解:(1)如图所示:过点D作DF∥AB,过点D作DN⊥AB于点N,EF⊥AB于点M,
由题意可得,四边形DNMF是矩形,
则∠NDF=90°,
∵∠A=60°,∠AND=90°,
∴∠ADN=30°,
∴∠EDF=135°﹣90°﹣30°=15°,
即DE与水平桌面(AB所在直线)所成的角为15°;
(2)如图所示:∵∠ACB=90°,∠A=60°,AB=16cm,
∴∠ABC=30°,则AC=AB=8cm,
∵灯杆CD长为40cm,
∴AD=48cm,
∴DN=AD cos30°≈41.76cm,
则FM=41.76cm,
∵灯管DE长为15cm,
∴sin15°===0.26,
解得:EF=3.9,
故台灯的高为:3.9+41.76≈45.7(cm).
18.解:延长AD交BE的延长线于点F,则∠F=30°,
∵∠DCE=45°,DE⊥CF,CD=2
米,
∴CE=DE=2,
在直角三角形DEF中,EF==2
米,
∴BF=BC+CE+EF=(10+2
)米,
在直角三角形ABF中,AB=BF×tan30°=+2≈7.77米.
19.解:过点C作CF∥DA交AB于点F.
∵MN∥PQ,CF∥DA,
∴四边形AFCD是平行四边形.
∴AF=CD=50m,∠CFB=35°.
∴FB=AB﹣AF=130﹣50=80(m),
设BE=x,∵∠CBN=60°,
∴EC=x,
∴tan35°=≈0.7,
即=0.7,
解得:x=56,
∴CE=56×1.7≈95.2≈95(m),
答:河流的宽是95米.
20.解:(1)在Rt△BOP中,∠BOP=90°,
∵∠BPO=45°,OP=100,
∴OB=OP=100.
在Rt△AOP中,∠AOP=90°,
∵∠APO=60°,
∴AO=OP tan∠APO.
∴A0=100,
AB=100(﹣1)(米);
(2)∵此车的速度==25(﹣1)≈25×0.73=18.25米/秒,
54千米/小时=≈15米/秒,
15米/秒<18.25米/秒,
∴此车超过了永丰路每小时54千米的限制速度.
21.解:(1)作AM⊥EF于点M,作BN⊥EF于点N,如右图所示,
∴AB=MN,
∵∠ACF=45°,
∴CM=AM=60米,
在Rt△BDF中,∵tan∠BDF=,
∴DN=米,
∵CM+MN=CD+DN,
∴CD=60+x﹣28.04=31.96+x;
(2)当CD=100米时,
则100=31.96+x,
解得:x=100﹣31.96≈68米,
即AB=68米.
22.解:(1)∵在RT△ACD中,AC=45cm,DC=60cm,
∴AD==75,
∴车架档AD的长为75cm,
(2)过点E作EF⊥AB,垂足为点F,
∵AE=AC+CE=45+20(cm)
∴EF=AEsin75°=(45+20)sin75°≈62.7835≈63cm,
∴车座点E到车架档AB的距离是63cm.
23.解:(1)过点C作CG∥DE,过点A作AH⊥CG于H,过点C作CF⊥DE于点F,
则点A到直线DE的距离为:AH+CF.
在Rt△CDF中,
∵sin∠CDE=,
∴CF=CD sin60°=70×=35≈59.5(mm).
∵∠DCB=70°,
∴∠ACD=180°﹣∠DCB=110°,
∵CG∥DE,
∴∠GCD=∠CDE=60°.
∴∠ACH=∠ACD﹣∠DCG=50°.
在Rt△ACH中,
∵sin∠ACH=,
∴AH=AC sin∠ACH=(115﹣35)×sin50°≈80×0.8=64(mm).
∴点A到直线DE的距离为AH+CF=59.5+64=123.5≈124(mm).
(2)如下图所示,虚线部分为旋转后的位置,B的对应点为B′,C的对应点为C′,
则B′C′=BC=35
mm,DC′=DC=70
mm.
在Rt△B′C′D中,
∵tan∠B′DC′==0.5,tan26.6°≈0.5,
∴∠B′DC′=26.6°.
∴CD旋转的角度为∠CDC′=∠CDE﹣∠B′DC′=60°﹣26.6°=33.4°.
24.解:(1)过点A作AG⊥CF于点G,如图2所示:
∵∠AEF=∠EFG=∠FGA=90°,
∴四边形AEFG为矩形,
∴FG=AE=3.5m,∠EAG=90°,
∴∠CAG=∠CAE﹣∠EAG=120°﹣90°=30°,
∴CG=AC=×12=6(m),
∴CF≈CG+FG=6+3.5=9.5(m),
∴云梯消防车最高点C距离地面的高为9.5m;
(2)由(1)得:FG=AE=3.5m,∠EAG=90°,
在Rt△ACG中,sin∠CAG=,
∴AC与∠CAG(0°<∠CAG<90°时)越大,CG越大,
∵90°≤∠CAE≤150°,10m≤AC≤20m,
∴∠CAG最大为:150°﹣90°=60°,AC最大为20m,
此时,CG=AC sin60°=20×≈17.32(m),
∴CF=CG+FG=17.32+3.5=20.82(m),
∴最高救援高度为20.82m,
∵20.82m>20m,
∴该消防车能实施有效救援.
25.解:(1)如图,过F点作FH⊥CD,垂足为H,
在Rt△FCH中,∠FCH=45°,
∴FH=CH,
在Rt△FDH中,
∵∠FHD=﹣90°,∠HDF=30°,DF=30cm
∴FH=DF=15(cm)=CH,
DH=DF=15(cm),
∴CD=CH+HD=(15+15)cm,
∵CE:CD=1:3,
∴CE=CD=(5+5)cm,
∴ED=EC+CD=(20+20)cm,
又∵AB=BC=ED,
∴AC=2ED=(40+40)cm,
答:AC的距离为(40+40)cm;
(2)如图,过点A作AG⊥ED,交ED的延长线于点G,
在Rt△ACG中,
∵∠AGC=90°,∠ACG=45°,AC=(40+40)cm,
∴AG=AC=(20+20)cm,
答:拉杆端点A到水平滑杆ED的距离为(20+20)cm.
26.解:(1)由题意可得:cos∠FHE==,
则∠FHE=60°;
(2)延长FE交CB的延长线于M,过A作AG⊥FM于G,
∴HE∥AG,
∴∠FAG=∠FHE=60°,
在Rt△AGF中,
∵∠FAG=∠FHE=60°,sin∠FAG=,
∴sin60°==,
∴FG≈2.17(米),
∴GM=FM﹣FG=4.4﹣2.17=2.23(米),
∴AB=GM=2.23(米),
在Rt△ABC中,
∵tan∠CAB=,
∴BC=AB tan15°≈0.27×2.23≈0.6(米),
答:底座BC的长0.6米.
一、选择题
1.如图,电线杆的高度为CD=m,两根拉线AC与BC互相垂直(A,D,B在同一条直线上),若∠CBA=α,则拉线AC的长度可以表示为( )
A.
B.
C.mcosα
D.
2.如图四边形ABCD中,∠B=∠C=90°,CD=2米,BC=5米,,则AB=( )
A.8米
B.10米
C.12米
D.14米
3.图1是某公园的一个滑梯,图2是其示意图.滑梯的高BC为2m,坡角∠A为60°,由于滑梯坡角过大存在安全隐患,公园管理局决定对滑梯进行整改,要在高度不变的前提下,通过加长滑梯的水平距离AB,使得坡角∠A满足30°≤∠A≤45°,则AB加长的距离可以是( )
(参考数据:≈1.414,≈1.732)
A.0.8m
B.1.6m
C.2.4m
D.3.2m
4.如图,一名滑雪运动员沿着倾斜角为34°的斜坡,从A滑行至B,已知AB=500米,则这名滑雪运动员的高度下降了( )米.(sin34°≈0.56,cos34°≈0.83,tan34°≈0.67)
A.415
B.280
C.335
D.250
二、填空题
5.小明用一块含有60°(∠DAE=60°)的直角三角尺测量校园内某棵树的高度,示意图如图所示,若小明的眼睛与地面之间的垂直高度AB为1.62m,小明与树之间的水平距离BC为4m,则这棵树的高度约为
m.(结果精确到0.1m,参考数据:≈1.73)
6.如图,地面上两个村庄C、D处于同一水平线上,一飞行器在空中以12千米/小时的速度沿MN方向水平飞行,航线MN与C、D在同一铅直平面内.当该飞行器飞至村庄C的正上方A处时,测得∠NAD=60°,该飞行器从A处飞行40分钟至B处时,测得∠ABD=75°,则村庄C、D间的距离为
千米.(≈1.732,结果保留一位小数)
7.如图,同学们利用所学知识去测量三江源某河段某处的宽度,小明同学在A处观测对岸点C.测得∠CAD=45°,小刚同学在距点A处60米远的B点测得∠CBD=30°,根据这些数据可以算出河宽为
米(精确到0.01米,≈1.414,≈1.732).
8.如图,一架长为10米的梯子AB斜靠在一竖直的墙AO上,这时测得∠ABO=70°,如果梯子的底端B外移到D,则梯子顶端A下移到C,这时又测得∠CDO=50°,那么AC的长度约为
米.(sin70°≈0.94,sin50°≈0.77,cos70°≈0.34,cos50°≈0.64)
9.某型号飞机的机翼形状如图所示,根据图中数据计算AB的长度为
.(结果保留小数点后两位,≈1.732)
10.某高铁路段修建过程中需要经过一座小山.如图,施工方计划沿AC方向开挖隧道,为了加快施工速度,要在小山的另一侧D处(A、C、D共线)同时施工.测得∠CAB=30°,AB=4km,∠ABD=105°,则BD的长为
.(结果保留根号)
11.如图是高铁站自动检票口的双翼闸机,检票后双翼收起,通过闸机的物体的最大宽度为70cm,检票前双翼展开呈扇形CAP和扇形DBQ,若AC=BD=55cm,∠PCA=∠BDQ=30°,则A、B之间的距离为
cm.
12.如图,是矗立在高速公路水平地面上的交通警示牌,经测量得到如下数据:AM=4米,AB=8米,∠MAD=45°,∠MBC=30°,则警示牌的高CD为
米(结果精确到0.1,参考数据:=1.41,=1.73)
13.如图,由游客中心A处修建通往百米观景长廊BC的两条栈道AB,AC.若∠B=56°,∠C=45°,则游客中心A到观景长廊BC的距离AD的长约为
米.(结果保留整数,sin56°≈0.8,tan56°≈1.5)
14.如图,某商场大厅自动扶梯AB的长为12m,它与水平面AC的夹角∠BAC=30°,则大厅两层之间的高度BC为
m.
15.如图,某水库水坝的坝高为24米,如果迎水坡AB的坡度为1:0.75,那么该水库迎水坡AB的长度为
米.
16.如图,我市在建高铁的某段路基横断面为梯形ABCD,DC∥AB.BC长6米,坡角β为45°,AD的坡角α为30°,则AD长为
米(结果保留根号).
三、解答题
17.如图(1)是一种简易台灯,在其结构图(2)中灯座为△ABC(BC伸出部分不计),A、C、D在同一直线上.量得∠ACB=90°,∠A=60°,AB=16cm,∠ADE=135°,灯杆CD长为40cm,灯管DE长为15cm.
(1)求DE与水平桌面(AB所在直线)所成的角;
(2)求台灯的高(点E到桌面的距离,结果精确到0.1cm).
(参考数据:sin15°=0.26,cos15°=0.97,tan15°=0.27,sin30°=0.5,cos30°=0.87,tan30°=0.58.)
18.如图,有一电线杆AB直立于地面,它的影子正好射在地面BC段和与地面成45°角的土坡CD上,已知∠BAD=60°,BC=8米,CD=2米,求电线杆AB的高.(结果保留3个有效数字,≈1.732)
19.如图,河流的两岸PQ、MN互相平行,河岸PQ上有一排小树,已知相邻两树之间的距离CD=50米,某人在河岸MN的A处测的∠DAN=35°,然后沿河岸走了130米到达B处,测的∠CBN=60°,求河流的宽度CE(结果保留整数).
(参考数据:sin35°≈0.6,cos35°≈0.8,tan35°≈0.7,≈1.7)
20.超速行驶是引发交通事故的主要原因.上周末,小明和三位同学尝试用自己所学的知识检测车速,如图,观测点设在到永丰路的距离为100米的点P处.这时,一辆小轿车由西向东匀速行驶,测得此车从A处行驶到B处所用的时间为4秒,∠APO=60°,∠BPO=45°.
(1)求A、B之间的路程;
(2)请判断此车是否超过了永丰路每小时54千米的限制速度?(参考数据:≈1.73)
21.小明同学想测量位于池塘两端的A、B两点的距离.他沿着与直线AB平行的道路EF行走,当行走到点C处,测得∠ACF=45°,再向前行走一段距离时到点D处,侧得∠BDF=65°.若直线AB与EF之间的距离为60米.
(1)设池塘两端的距离AB=x米,试用含x的代数式表示CD的长;
(2)当CD=100米时,求A、B两点的距离(计算结果精确到个位).(参考数据:sin45°≈0.71,cos65°≈0.42,tan65°≈2.14.)
22.“低碳生活,绿色出行”,自行车正逐渐成为人们喜爱的交通工具,如图1所示是一辆自行车的实物图,车架档AC与CD的长分别为45cm,60cm,且它们互相垂直,座杆CE的长为20cm,点A,C,E在同一条直线上,且∠CAB=75°,如图2.
(1)求车架档AD的长;
(2)求车座点E到车架档AB的距离(结果精确到1cm,参考数据sin75°=0.966,cos75°=0.259,tan75°=3.732)
23.图①是一种手机平板支架,由托板、支撑板和底座构成,手机放置在托板上,图②是其侧面结构示意图,托板长AB=115mm,支撑板长CD=70mm,板AB固定在支撑板顶点C处,且CB=35mm,托板AB可绕点C转动,支撑板CD可绕点D转动,∠CDE=60°.
(1)若∠DCB=70°时,求点A到直线DE的距离(计算结果精确到个位);
(2)为了观看舒适,把(1)中∠DCB=70°调整为90°,再将CD绕点D逆时针旋转,使点B落在直线DE上即可,求CD旋转的角度.
(参考数据:sin50°≈0.8,cos50°≈0.6,tan50°≈1.2,sin26.6°≈0.4,cos26.6°≈0.9,tan26.6°≈0.5,≈1.7)
24.已知,图1是一辆登高云梯消防车的实物图,图2是其工作示意图,起重臂AC可伸缩(10m≤AC≤20m),且起重臂AC可绕点A在一定范围内转动,张角为∠CAE(90°≤∠CAE≤150°),转动点A距离地面BD的高度AE为3.5m.
(1)当起重臂AC长度为12m,张角∠CAE为120°时,求云梯消防车最高点C距离地面的高;
(2)某日,一居民家突发险情,该居民家距离地面的高度为20m,请问该消防车能否实施有效救援?(参考数据:≈1.732)
25.小慧要外出参加活动,需网购拉杆箱,图①,图②分别是她在网上看到的某型号拉杆箱实物图与示意图,并获得如下信息:滑杆DE、箱长BC、拉杆AB的长度相等,B、F在AC上,C在DE上,支杆DF=30cm,CE:CD=1:3,∠DCF=45°,∠CDF=30°,请根据以上信息,解决下列问题:
(1)求AC的长度(结果保留根号);
(2)求拉杆端点A到水平滑杆ED的距离(结果保留根号).
26.如图1,2分别是某款篮球架的实物图与示意图,已知支架AB与支架AC所成的角∠BAC=15°,点A、H、F在同一条直线上,支架AH段的长为1米,HF段的长为1.50米,篮板底部水平支架HE的长为0.75米,篮板顶端F到地面的距离为4.4米.
(1)求篮板底部支架HE与支架AF所成的角∠FHE的度数.
(2)求底座BC的长.(结果精确到0.1米;参考数据:sin15°≈0.26,cos15°≈0.97,tan15°=0.27,≈1.732,≈1.414)
参考答案
1.解:∵∠ACD+∠BCD=90°,∠CBD+∠BCD=90°,
∴∠ACD=∠CBD,
在Rt△ACD中,∵cos∠ACD=,
∴AC=,
故选:B.
2.解:过D作DE⊥AB于E,
∴∠DEB=∠B=∠C=90°,
∴四边形DEBC是矩形,
∴BE=DC=2米,DE=BC=5米,
∵sinA=,
∴,
∴AD=13(米),
∴AE=(米),
∴AB=AE+BE=12+2=14(米),
故选:D.
3.解:如图,在Rt△ABC,∠CAB=60°,BC=2m,
∴AB===,
当坡角为45°时,有BD=BC=2m,
∴DA=2﹣AB=2﹣≈0.85(m),
当坡角为30°时,有BE===2(m),
∴EA=BE﹣AB=2﹣≈2.31(m),
当坡角满足30°≤∠A≤45°,
∴AB加长的距离x的取值范围为0.85≤x≤2.31m,
故选:B.
4.解:在Rt△ABC中,∠ABC=34°,sin∠ABC=,
∴AC=AB sin34°≈500×0.56≈280(米),
∴这名滑雪运动员的高度下降了280米,
故选:B.
5.解:∵AB⊥BC,DC⊥BC,AD∥BC,
∴四边形ABCD是矩形,
∵BC=4m,AB=1.62m,
∴AD=BC=4m,DC=AB=1.62m,
Rt△AED中,∵∠DAE=60°,AD=4m,
∴ED=AD tan60°=4×=4(m),
∴CE=ED+DC=4+1.62≈8.5(m)
答:这棵树的高度约为8.5m.
故答案为:8.5.
6.解:如图,过B作BE⊥AD于E,
∵∠NAD=60°,∠ABD=75°,
∴∠ADB=45°,
∵AB=12×=8(千米),
∴AE=4(千米).BE=4(千米),
∴DE=BE=4(千米),
∴AD=(4+4)(千米),
∵∠C=90,∠CAD=30°,
∴CD=AD=2+2≈5.5(千米).
故答案为:5.5.
7.解:过C作CE⊥AB于E,设CE=x米,
在Rt△AEC中,∠CAE=45°,
∴AE=CE=x米,
在Rt△BCE中,∠CBE=30°,
∴BE=CE=x(米),
∴x=x+60,
解得,x=30+30≈81.96(米).
答:河宽约为81.96米.
故答案为:81.96.
8.解:由题意可得:
∵∠ABO=70°,AB=10m,
∴sin70°=,
解得:AO=9.4(m),
∵∠CDO=50°,DC=10m,
∴sin50°=≈0.77,
解得:CO=7.7(m),
则AC=9.4﹣7.7=1.70(m),
答:AC的长度约为1.70米.
故答案为:1.70.
9.解:如图,
在Rt△CEA中,∵cos∠ECA=,
∴CA=≈7.07(m);
在Rt△BDF中,∵cos∠BDF=,
∴DB=≈5.77(m),
∴BF=BD≈2.89(m),
∵AB+AE=EF+BF,
∴AB=3.4+2.89﹣5=1.29(m).
故答案为:1.29m.
10.解:过B作BE⊥AD于点E,
∵∠CAB=30°,AB=4km,
∴∠ABE=60°,BE=2km,
∵∠ABD=105°,
∴∠EBD=45°,
∴∠EDB=45°,
∴BE=DE=2km,
∴BD===2(km),
即BD的长是2km.
11.解:如图,连接AB,CD,过点A作AE⊥CD于E,过点B作BF⊥CD于F.
则CD=70cm,四边形AEFB是矩形,
∴EF=AB,
∵AE∥PC,
∴∠PCA=∠CAE=30°,
∴CE=AC sin30°=55×=(cm),
同理可得DF=(cm),
∴AB=EF=CD﹣CE﹣DF=70﹣﹣=15(cm),
故答案为:15.
12.解:由题意可得:∵AM=4米,∠MAD=45°,
∴DM=4m,
∵AM=4米,AB=8米,
∴MB=12米,
∵∠MBC=30°,
∴BC=2MC,
∴MC2+MB2=(2MC)2,
MC2+122=(2MC)2,
∴MC=4,
则DC=4﹣4≈2.9(米),
故答案为:2.9.
13.解:∵∠B=56°,∠C=45°,∠ADB=∠ADC=90°,BC=BD+CD=100米,
∴BD=,CD=,
∴+=100,
解得AD≈60.
故答案为:60.
14.解;在Rt△ABC中,∠BAC=30°,AB=12m,
∴BC=m,
故答案为:6.
15.解:如图,过点B作BC垂直于水平面于点C,
∵迎水坡AB的坡度为1:0.75
∴BC:AC=1:0.75,
∴24:AC=1:0.75,
∴AC=18(米),
∴AB=
==30(米),
即该大坝迎水坡AB的长度为30米,
故答案为:30.
16.解:过点D作DE⊥AB于E,过点C作CF⊥AB于F.
∵CD∥AB,DE⊥AB,CF⊥AB,
∴DE=CF,
在Rt△CFB中,CF=BC sin45°=3(米),
∴DE=CF=3(米),
在Rt△ADE中,∵∠A=30°,∠AED=90°,
∴AD=2DE=6(米),
故答案为:6.
17.解:(1)如图所示:过点D作DF∥AB,过点D作DN⊥AB于点N,EF⊥AB于点M,
由题意可得,四边形DNMF是矩形,
则∠NDF=90°,
∵∠A=60°,∠AND=90°,
∴∠ADN=30°,
∴∠EDF=135°﹣90°﹣30°=15°,
即DE与水平桌面(AB所在直线)所成的角为15°;
(2)如图所示:∵∠ACB=90°,∠A=60°,AB=16cm,
∴∠ABC=30°,则AC=AB=8cm,
∵灯杆CD长为40cm,
∴AD=48cm,
∴DN=AD cos30°≈41.76cm,
则FM=41.76cm,
∵灯管DE长为15cm,
∴sin15°===0.26,
解得:EF=3.9,
故台灯的高为:3.9+41.76≈45.7(cm).
18.解:延长AD交BE的延长线于点F,则∠F=30°,
∵∠DCE=45°,DE⊥CF,CD=2
米,
∴CE=DE=2,
在直角三角形DEF中,EF==2
米,
∴BF=BC+CE+EF=(10+2
)米,
在直角三角形ABF中,AB=BF×tan30°=+2≈7.77米.
19.解:过点C作CF∥DA交AB于点F.
∵MN∥PQ,CF∥DA,
∴四边形AFCD是平行四边形.
∴AF=CD=50m,∠CFB=35°.
∴FB=AB﹣AF=130﹣50=80(m),
设BE=x,∵∠CBN=60°,
∴EC=x,
∴tan35°=≈0.7,
即=0.7,
解得:x=56,
∴CE=56×1.7≈95.2≈95(m),
答:河流的宽是95米.
20.解:(1)在Rt△BOP中,∠BOP=90°,
∵∠BPO=45°,OP=100,
∴OB=OP=100.
在Rt△AOP中,∠AOP=90°,
∵∠APO=60°,
∴AO=OP tan∠APO.
∴A0=100,
AB=100(﹣1)(米);
(2)∵此车的速度==25(﹣1)≈25×0.73=18.25米/秒,
54千米/小时=≈15米/秒,
15米/秒<18.25米/秒,
∴此车超过了永丰路每小时54千米的限制速度.
21.解:(1)作AM⊥EF于点M,作BN⊥EF于点N,如右图所示,
∴AB=MN,
∵∠ACF=45°,
∴CM=AM=60米,
在Rt△BDF中,∵tan∠BDF=,
∴DN=米,
∵CM+MN=CD+DN,
∴CD=60+x﹣28.04=31.96+x;
(2)当CD=100米时,
则100=31.96+x,
解得:x=100﹣31.96≈68米,
即AB=68米.
22.解:(1)∵在RT△ACD中,AC=45cm,DC=60cm,
∴AD==75,
∴车架档AD的长为75cm,
(2)过点E作EF⊥AB,垂足为点F,
∵AE=AC+CE=45+20(cm)
∴EF=AEsin75°=(45+20)sin75°≈62.7835≈63cm,
∴车座点E到车架档AB的距离是63cm.
23.解:(1)过点C作CG∥DE,过点A作AH⊥CG于H,过点C作CF⊥DE于点F,
则点A到直线DE的距离为:AH+CF.
在Rt△CDF中,
∵sin∠CDE=,
∴CF=CD sin60°=70×=35≈59.5(mm).
∵∠DCB=70°,
∴∠ACD=180°﹣∠DCB=110°,
∵CG∥DE,
∴∠GCD=∠CDE=60°.
∴∠ACH=∠ACD﹣∠DCG=50°.
在Rt△ACH中,
∵sin∠ACH=,
∴AH=AC sin∠ACH=(115﹣35)×sin50°≈80×0.8=64(mm).
∴点A到直线DE的距离为AH+CF=59.5+64=123.5≈124(mm).
(2)如下图所示,虚线部分为旋转后的位置,B的对应点为B′,C的对应点为C′,
则B′C′=BC=35
mm,DC′=DC=70
mm.
在Rt△B′C′D中,
∵tan∠B′DC′==0.5,tan26.6°≈0.5,
∴∠B′DC′=26.6°.
∴CD旋转的角度为∠CDC′=∠CDE﹣∠B′DC′=60°﹣26.6°=33.4°.
24.解:(1)过点A作AG⊥CF于点G,如图2所示:
∵∠AEF=∠EFG=∠FGA=90°,
∴四边形AEFG为矩形,
∴FG=AE=3.5m,∠EAG=90°,
∴∠CAG=∠CAE﹣∠EAG=120°﹣90°=30°,
∴CG=AC=×12=6(m),
∴CF≈CG+FG=6+3.5=9.5(m),
∴云梯消防车最高点C距离地面的高为9.5m;
(2)由(1)得:FG=AE=3.5m,∠EAG=90°,
在Rt△ACG中,sin∠CAG=,
∴AC与∠CAG(0°<∠CAG<90°时)越大,CG越大,
∵90°≤∠CAE≤150°,10m≤AC≤20m,
∴∠CAG最大为:150°﹣90°=60°,AC最大为20m,
此时,CG=AC sin60°=20×≈17.32(m),
∴CF=CG+FG=17.32+3.5=20.82(m),
∴最高救援高度为20.82m,
∵20.82m>20m,
∴该消防车能实施有效救援.
25.解:(1)如图,过F点作FH⊥CD,垂足为H,
在Rt△FCH中,∠FCH=45°,
∴FH=CH,
在Rt△FDH中,
∵∠FHD=﹣90°,∠HDF=30°,DF=30cm
∴FH=DF=15(cm)=CH,
DH=DF=15(cm),
∴CD=CH+HD=(15+15)cm,
∵CE:CD=1:3,
∴CE=CD=(5+5)cm,
∴ED=EC+CD=(20+20)cm,
又∵AB=BC=ED,
∴AC=2ED=(40+40)cm,
答:AC的距离为(40+40)cm;
(2)如图,过点A作AG⊥ED,交ED的延长线于点G,
在Rt△ACG中,
∵∠AGC=90°,∠ACG=45°,AC=(40+40)cm,
∴AG=AC=(20+20)cm,
答:拉杆端点A到水平滑杆ED的距离为(20+20)cm.
26.解:(1)由题意可得:cos∠FHE==,
则∠FHE=60°;
(2)延长FE交CB的延长线于M,过A作AG⊥FM于G,
∴HE∥AG,
∴∠FAG=∠FHE=60°,
在Rt△AGF中,
∵∠FAG=∠FHE=60°,sin∠FAG=,
∴sin60°==,
∴FG≈2.17(米),
∴GM=FM﹣FG=4.4﹣2.17=2.23(米),
∴AB=GM=2.23(米),
在Rt△ABC中,
∵tan∠CAB=,
∴BC=AB tan15°≈0.27×2.23≈0.6(米),
答:底座BC的长0.6米.
