2.6利用三角函数测高 能力达标测评 2021-2022学年九年级数学鲁教版(五四制)上册(word版含答案)
文档属性
| 名称 | 2.6利用三角函数测高 能力达标测评 2021-2022学年九年级数学鲁教版(五四制)上册(word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 426.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-05 08:29:19 | ||
图片预览



文档简介
2021-2022学年鲁教版九年级数学上册《2.6利用三角函数测高》能力达标测评(附答案)
一.选择题(共10小题,满分40分)
1.如图,已知公路l上A,B两点之间的距离为20m,已知B在C的南偏西30°的方向上,A在C的南偏西60°方向上,则点C到公路l的距离为( )
A.10m
B.m
C.10m
D.(10+10)m
2.如图,小明在C处看到西北方向上有一凉亭A,北偏东35°的方向上有一棵大树B,已知凉亭A在大树B的正西方向,若BC=100米,则A、B两点相距( )米.
A.100(cos35°+sin35°)
B.100(cos35°﹣sin35°)
C.(+)
D.(﹣)
3.如图为东西流向且河岸平行的一段河道,点A,B分别为两岸上一点,且点B在点A正北方向,由点A向正东方向走a米到达点C,此时测得点B在点C的北偏西55°方向上,则河宽AB的长为( )
A.atan55°米
B.米
C.米
D.米
4.如图,一艘海轮位于灯塔P的南偏东37°方向,距离灯塔40海里的A处,它沿正北方向航行一段时间后,到达位于灯塔的正东方向上的B处,这时,B处与灯塔P的距离PB的长可以表示为( )
A.40海里
B.40sin37°海里
C.40cos37°海里
D.40tan37°海里
5.如图,一艘轮船在A处测的灯塔C在北偏西15°的方向上,该轮船又从A处向正东方向行驶20海里到达B处,测的灯塔C在北偏西60°的方向上,则轮船在B处时与灯塔C之间的距离(即BC的长)为( )
A.40海里
B.(20+10)海里
C.40海里
D.(10+10)海里
6.如图,一渔船以32海里/时的速度向正北航行,在A处看到灯塔S在渔船的北偏东30°,半小时后航行到B处看到灯塔S在船的北偏东60°,若渔船继续向正北航行到C处时,此时渔船在灯塔S的正西方向,此时灯塔S与渔船的距离( )
A.16海里
B.18海里
C.8海里
D.8海里
7.如图,在A处测得点P在北偏东60°方向上,在B处测得点P在北偏东30°方向上,若AP=6千米,则A,B两点的距离为( )千米.
A.4
B.4
C.2
D.6
8.如图,某社会实践活动小组实地测量两岸互相平行的一段河的宽度,在河的南岸点A处,测得河的北岸边点B在其北偏东45°方向,然后向西走60米到达C点,测得点B在点C的北偏东60°方向,则这段河的宽度为( )
A.60()米
B.30()米
C.(90﹣30)米
D.30(﹣1)米
9.如图,一艘轮船从位于灯塔C的北偏东60°方向,距离灯塔60海里的小岛A出发,沿正南方向航行一段时间后,到达位于灯塔C的南偏东45°方向上的B处,这时轮船B与小岛A的距离是( )
A.30海里
B.60海里
C.120海里
D.(30+30)海里
10.如图,港口A在观测站O的正东方向,OA=6km,某船从港口A出发,沿北偏东15°方向航行一段距离后到达B处,此时从观测站O处测得该船位于北偏东60°的方向,则该船航行的距离(即AB的长)为( )
A.3km
B.3km
C.4
km
D.(3﹣3)km
二.填空题(共5小题,满分20分)
11.某数学小组三名同学运用自己所学的知识检测车速,他们将观测点设在一段笔直的公路旁且距公路100米的点A处,如图所示,直线l表示公路,一辆小汽车由公路上的B处向C处匀速行驶,用时5秒,经测量,点B在点A北偏东45°方向上,点C在点A北偏东60°方向上,这段公路最高限速60千米/小时,此车
(填“超速”或“没有超速”)(参考数据:≈1.732)
12.如图,在东西方向的海岸线上有A、B两个港口,甲货船从A港沿北偏东60°的方向以4海里/小时的速度出发,同时乙货船从B港沿西北方向出发,2小时后相遇在点P处,问乙货船每小时航行
海里.
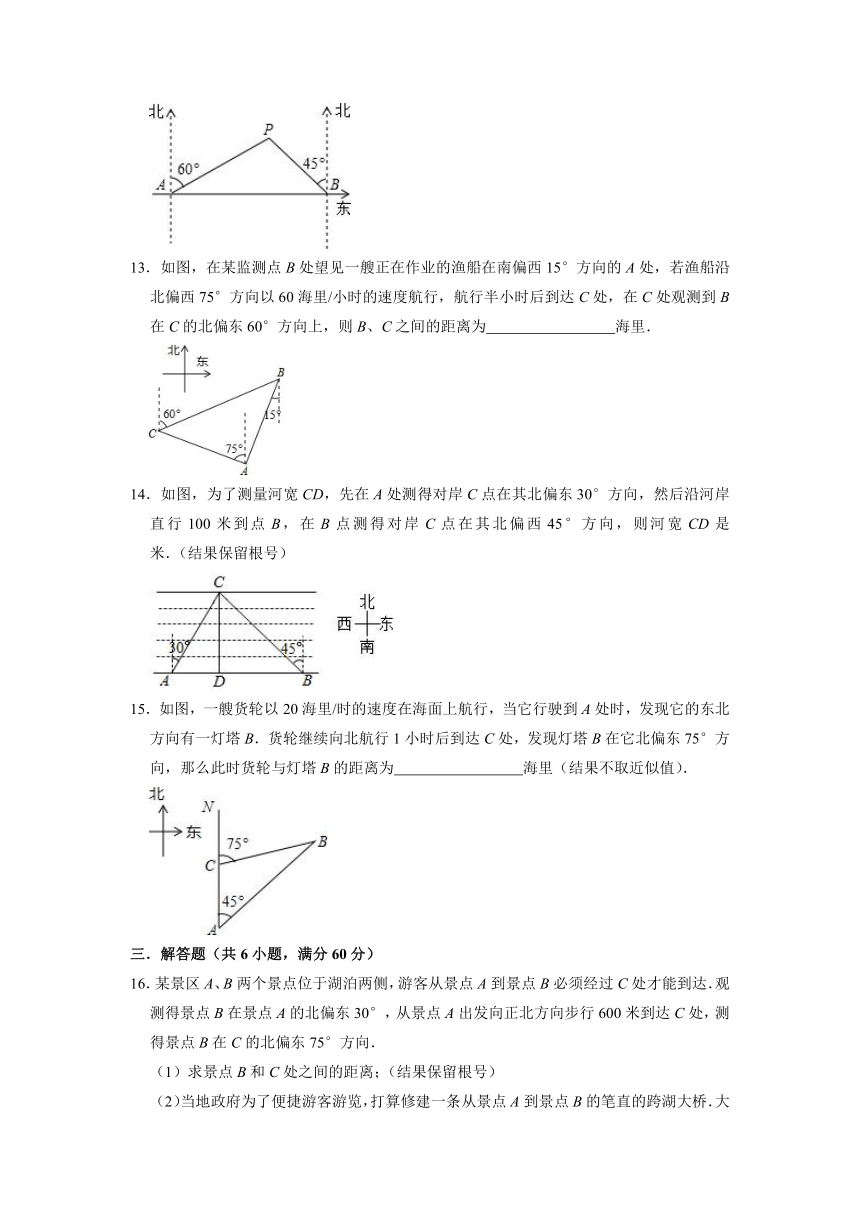
13.如图,在某监测点B处望见一艘正在作业的渔船在南偏西15°方向的A处,若渔船沿北偏西75°方向以60海里/小时的速度航行,航行半小时后到达C处,在C处观测到B在C的北偏东60°方向上,则B、C之间的距离为
海里.
14.如图,为了测量河宽CD,先在A处测得对岸C点在其北偏东30°方向,然后沿河岸直行100米到点B,在B点测得对岸C点在其北偏西45°方向,则河宽CD是
米.(结果保留根号)
15.如图,一艘货轮以20海里/时的速度在海面上航行,当它行驶到A处时,发现它的东北方向有一灯塔B.货轮继续向北航行1小时后到达C处,发现灯塔B在它北偏东75°方向,那么此时货轮与灯塔B的距离为
海里(结果不取近似值).
三.解答题(共6小题,满分60分)
16.某景区A、B两个景点位于湖泊两侧,游客从景点A到景点B必须经过C处才能到达.观测得景点B在景点A的北偏东30°,从景点A出发向正北方向步行600米到达C处,测得景点B在C的北偏东75°方向.
(1)求景点B和C处之间的距离;(结果保留根号)
(2)当地政府为了便捷游客游览,打算修建一条从景点A到景点B的笔直的跨湖大桥.大桥修建后,从景点A到景点B比原来少走多少米?(结果保留整数.参考数据:≈1.414,≈1.732)
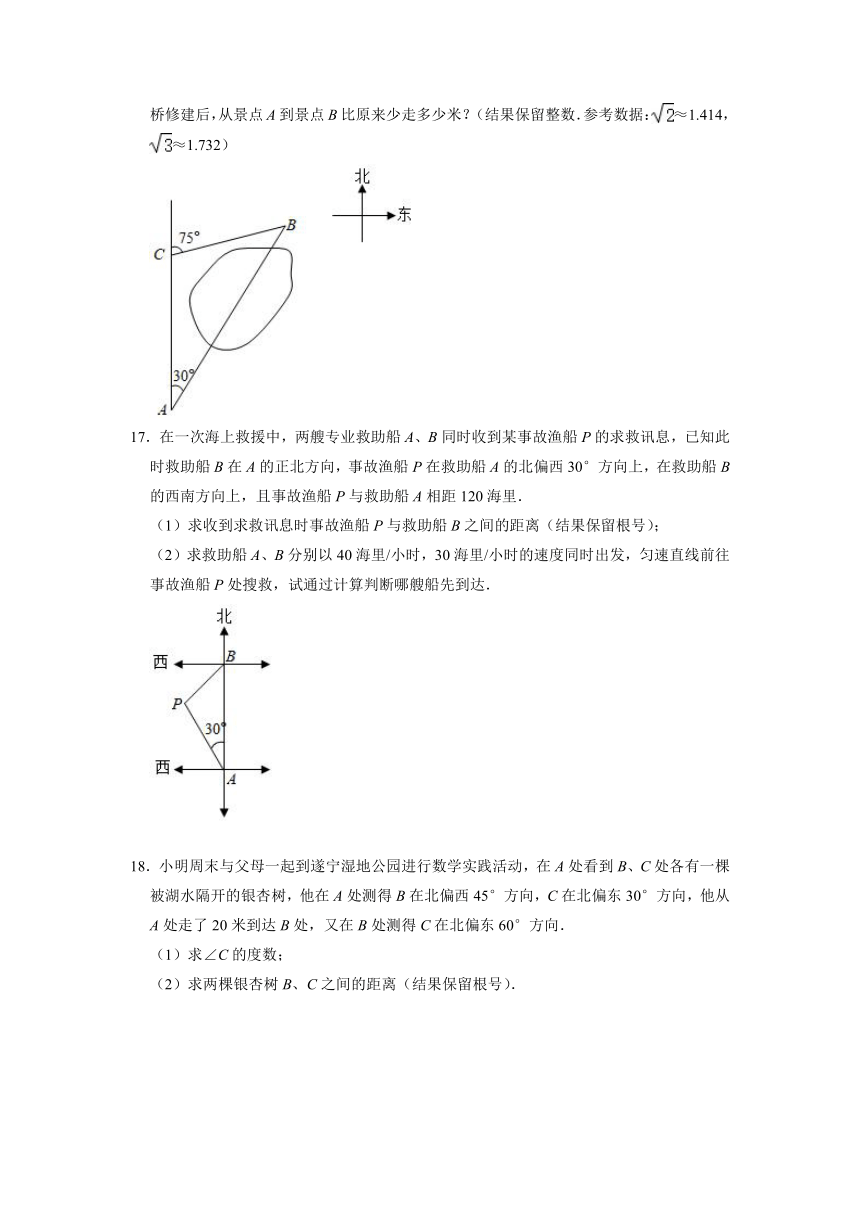
17.在一次海上救援中,两艘专业救助船A、B同时收到某事故渔船P的求救讯息,已知此时救助船B在A的正北方向,事故渔船P在救助船A的北偏西30°方向上,在救助船B的西南方向上,且事故渔船P与救助船A相距120海里.
(1)求收到求救讯息时事故渔船P与救助船B之间的距离(结果保留根号);
(2)求救助船A、B分别以40海里/小时,30海里/小时的速度同时出发,匀速直线前往事故渔船P处搜救,试通过计算判断哪艘船先到达.
18.小明周末与父母一起到遂宁湿地公园进行数学实践活动,在A处看到B、C处各有一棵被湖水隔开的银杏树,他在A处测得B在北偏西45°方向,C在北偏东30°方向,他从A处走了20米到达B处,又在B处测得C在北偏东60°方向.
(1)求∠C的度数;
(2)求两棵银杏树B、C之间的距离(结果保留根号).
19.如图,A,B是海面上位于东西方向的两个观测点,有一艘海轮在C点处遇险发出求救信号,此时测得C点位于观测点A的北偏东45°方向上,同时位于观测点B的北偏西60°方向上,且测得C点与观测点A的距离为25海里.
(1)求观测点B与C点之间的距离;
(2)有一艘救援船位于观测点B的正南方向且与观测点B相距30海里的D点处,在接到海轮的求救信号后立即前往营救,其航行速度为42海里/小时,求救援船到达C点需要的最少时间.
20.为了维护国家主权和海洋权力,海监部门对我国领海实现了常态化巡航管理.如图所示,正在执行巡航任务的海监船以每小时40海里的速度向正东方向航行,在A处测得灯塔P在北偏东60°方向上,继续航行30分钟后到达B处,此时测得灯塔P在北偏东45°方向上.
(1)求∠APB的度数;
(2)已知在灯塔P的周围25海里内有暗礁,问海监船继续向正东方向航行是否安全?(参考数据:≈1.414,≈1.732)
21.因东坡文化远近闻名的遗爱湖公园,“国庆黄金周”期间,游人络绎不绝,现有一艘游船载着游客在遗爱湖中游览,当船在A处时,船上游客发现岸上P1处的临摹亭和P2处的遗爱亭都在东北方向,当游船向正东方向行驶600m到达B处时,游客发现遗爱亭在北偏西15°方向,当游船继续向正东方向行驶400m到达C处时,游客发现临摹亭在北偏西60°方向.
(1)求A处到临摹亭P1处的距离;
(2)求临摹亭P1处与遗爱亭P2处之间的距离.(计算结果保留根号)
参考答案
一.选择题(共10小题,满分40分)
1.解:如图,过点C作CD⊥直线l于点D,
∴∠ADC=90°,
∵∠BCD=30°,∠ACD=60°,AB=20m,
∴∠ACB=∠ACD﹣∠BCD=60°﹣30°=30°,∠CAD=90°﹣∠ACD=90°﹣60°=30°,∠CBD=90°﹣∠BCD=90°﹣30°=60°,
∴∠ACB=∠CAD,
∴AB=BC=20m,
在Rt△BCD中,
∵sin∠CBD=,
∴CD=BC sin∠CBD=20×=10(m),
故选:C.
2.解:过点C作AB的垂线交AB于D,
∵B点在A点的正东方向上,
∴∠ACD=45°,∠DCB=35°,
在Rt△BCD中,BC=100,
∴DB=BCsin35°=100 sin35°(米),
CD=BCcos35°=100 cos35°(米),
在Rt△ACD中,AD=CD,
∴AB=AD+DB=100(sin35°+cos35°)(米).
故选:A.
3.解:连接AB,BC,
由题意得,∠BAC=90°,∠ABC=55°,AC=a米,
∴tan∠ABC=tan55°=,
∴AB==,
故选:D.
4.解:∵一艘海轮位于灯塔P的南偏东37°方向,
∴∠BAP=37°,
∵AP=40海里,
∴BP=AP sin37°=40sin37°海里;
故选:B.
5.解:过A作AD⊥BC于D,如图所示:
在Rt△ABD中,∠ABD=90°﹣60°=30°,AB=20海里,
∴AD=AB=10(海里),BD=AD=AB=10(海里),
∵∠ABC=90°﹣60°=30°,∠BAC=90°+15°=105°,
∴∠C=180°﹣105°﹣30°=45°,
∴△ACD是等腰直角三角形,
∴CD=AD=10(海里),
∴BC=BD+CD=(10+10)海里,
故选:D.
6.解:由题意得,AB=32×=16(海里),∠ACS=90°,
∵∠A=30°,∠CBS=60°,
∴∠ASB=∠CBS﹣∠A=30°,
∴∠ASB=∠A,
∴BS=AB=16(海里),
在Rt△CBS中,sin∠CBS=,
∴CS=BS sin∠CBS=16×=8(海里),
故选:D.
7.解:由题意知,∠PAB=30°,∠PBC=60°,
∴∠APB=∠PBC﹣∠PAB=60°﹣30°=30°,
∴∠PAB=∠APB,
∴AB=PB,
在Rt△PAC中,∵AP=6千米,
∴PC=PA=3千米,
在Rt△PBC中,∵sin∠PBC=,
∴PB===6千米.
故选:D.
8.解:作BD⊥CA交CA的延长线于D,
设BD=xm,
∵∠BCA=30°,
∴CD==x,
∵∠BAD=45°,
∴AD=BD=x,
则x﹣x=60,
解得x==30(),
答:这段河的宽约为30()米.
故选:B.
9.解:过C作CD⊥AB于D,
∴∠ACD=30°,∠BCD=45°,AC=60海里,
在Rt△ACD中,AD=AC=30(海里),cos∠ACD=,
∴CD=AC cos∠ACD=60×=30(海里),
在Rt△DCB中,∵∠BCD=∠B=45°,
∴CD=BD=30(海里),
∴AB=AD+BD=(30+30)海里,
答:这时轮船B与小岛A的距离是(30+30)海里.
故选:D.
10.解:作AC⊥OB于点C,如右图所示,
由已知可得,
∠COA=30°,OA=6km,
∵AC⊥OB,
∴∠OCA=∠BCA=90°,
∴OA=2AC,∠OAC=60°,
∴AC=3km,∠CAD=30°,
∵∠DAB=15°,
∴∠CAB=45°,
∴∠CAB=∠B=45°,
∴BC=AC,
∴AB=,
故选:A.
二.填空题(共5小题,满分20分)
11.解:作AD⊥直线l于D,
在Rt△ADB中,∠ABD=45°,
∴BD=AD=100,
在Rt△ADB中,tan∠ACD=,
则CD==100≈173.2,
∴BC=173.2﹣100=73.2(米),
小汽车的速度为:0.0732÷=52.704(千米/小时),
∵52.704千米/小时<60千米/小时,
∴小汽车没有超速,
故答案为:没有超速.
12.解:作PC⊥AB于点C,
∵甲货船从A港沿北偏东60°的方向以4海里/小时的速度出发,
∴∠PAC=30°,AP=4×2=8,
∴PC=AP×sin30°=8×=4.
∵乙货船从B港沿西北方向出发,
∴∠PBC=45°,
∴PB=PC÷=4,
∴乙货船每小时航行4÷2=2海里/小时,
故答案为2.
13.解:由题意得,AC=60×0.5=30海里,
∵CD∥BF,
∴∠CBF=∠DCB=60°,又∠ABF=15°,
∴∠ABC=45°,
∵AE∥BF,
∴∠EAB=∠FBA=15°,又∠EAC=75°,
∴∠CAB=90°,
∴BC=AC=30海里,
故答案为:30.
14.解:设CD=x米,
由题意得:CD⊥AB,∠ACD=30°,∠BCD=45°,
∴∠ADC=∠BDC=90°,
∴AD=CD=x米,BD=CD=x米,
∵AD+BD=AB=100米,
∴x+x=100,
解得:x=150﹣50,
即河宽CD是(150﹣50)米,
故答案为:(150﹣50).
15.解:作CE⊥AB于E,
20海里/时×1小时=20海里,
∴AC=20海里,
∵∠A=45°,
∴CE=AC sin45°=10,
∵∠NCB=75°,∠A=45°,
∴∠B=30°,
∴BC===20海里,
故答案为:20.
三.解答题(共6小题,满分60分)
16.解:(1)过点C作CD⊥AB于点D,
由题意得,∠A=30°,∠BCE=75°,AC=600m,
在Rt△ACD中,∠A=30°,AC=600,
∴CD=AC=300(m),
AD=AC=300(m),
∵∠BCE=75°=∠A+∠B,
∴∠B=75°﹣∠A=45°,
∴CD=BD=300(m),
BC=CD=300(m),
答:景点B和C处之间的距离为300m;
(2)由题意得.
AC+BC=(600+300)m,
AB=AD+BD=(300+300)m,
AC+BC﹣AB=(600+300)﹣(300+300)
≈204.6
≈205(m),
答:大桥修建后,从景点A到景点B比原来少走约205m.
17.解:(1)作PC⊥AB于C,如图所示:
则∠PCA=∠PCB=90°,
由题意得:PA=120海里,∠A=30°,∠CBP=45°,
在Rt△ACP中,∵∠CAP=30°,∠PCA=90°,
∴PC=PA=60海里,
在Rt△BCP中,∵∠PCB=90°,∠CBP=45°,sin∠CBP=,
∴PB===60(海里),
答:收到求救讯息时事故渔船P与救助船B之间的距离为60海里;
(2)∵PA=120海里,PB=60海里,救助船A,B分别以40海里/小时、30海里/小时的速度同时出发,
∴救助船A所用的时间为=3(小时),救助船B所用的时间为=2(小时),
∵3>2,
∴救助船B先到达.
18.解:(1)设AD与BC交于点F,
由题意得BE∥AD,
∵BE∥AD且∠EBF=60°,
∴∠BFA=∠EBF=60°,
∵∠BFA=∠C+∠CAD且∠CAD=30°,
∴∠C=∠BFA﹣∠CAD=30°;
(2)过点B作BG⊥AD于G.
∵BG⊥AD,
∴∠AGB=∠BGD=90°,
在Rt△AGB中,AB=20米,∠BAG=45°,
AG=BG=20×sin45°=(米),
在Rt△BGF中,∠BFG=60°,
∴BF=BGsin60°=(米),FG=BGtan60°=(米),
∵∠C=∠CAD=30°,
∴CF=AF=AG+FG=(10+)(米),
∴BC=BF+CF=(10+10)米,
答:两棵银杏树B、C之间的距离为
()米.
19.解:(1)如图,过点C作CE⊥AB于点E,
根据题意可知:∠ACE=∠CAE=45°,AC=25海里,
∴AE=CE=25(海里),
∵∠CBE=30°,
∴BE=25(海里),
∴BC=2CE=50(海里).
答:观测点B与C点之间的距离为50海里;
(2)如图,作CF⊥DB于点F,
∵CF⊥DB,FB⊥EB,CE⊥AB,
∴四边形CEBF是矩形,
∴FB=CE=25(海里),CF=BE=25(海里),
∴DF=BD+BF=30+25=55(海里),
在Rt△DCF中,根据勾股定理,得
CD===70(海里),
∴70÷42=(小时).
答:救援船到达C点需要的最少时间是小时.
20.解:(1)由题意得,∠PAB=90°﹣60°=30°,∠ABP=90°+45°=135°,
∴∠APB=180°﹣∠PAB﹣∠ABP=180°﹣30°﹣135°=15°;
(2)海监船继续向正东方向航行安全,理由如下:
作PH⊥AB于H,如图:
则△PBH是等腰直角三角形,
∴BH=PH,
设BH=PH=x海里,
由题意得:AB=40×=20(海里),
在Rt△APH中,tan∠PAB=tan30°==,
即=,
解得:x=10+10≈27.32>25,且符合题意,
∴海监船继续向正东方向航行安全.
21.解:(1)作P1M⊥AC于M,
设P1M=xm,
在Rt△P1AM中,∵∠P1AB=45°,
∴AM=P1M=xm,
在Rt△P1CM中,∵∠P1CA=30°,
∴MC==xm,
∵AC=1000
m,
∴x+=1000,解得x=500(﹣1)(m),
∴P1M=500(﹣1)m
∴P1A==500(﹣)m,
故A处到临摹亭P1处的距离为500(﹣)m;
(2)作BN⊥AP2于N,
∵∠P2AB=45°,∠P2BA=75°,
∴∠P2=60°,
在Rt△ABN中,∵∠P1AB=45°,AB=600
m
∴BN=AN=AB=300
m,
∴P1N=500(﹣)﹣300=(500﹣800)
(m),
在Rt△P2BN中,∵∠P2=60°,
∴P2N=BN=×=100
(m),
∴P1P2=100﹣(500﹣800)=(800﹣400)
(m).
故临摹亭P1处与遗爱亭P2处之间的距离是(800﹣400)m.
一.选择题(共10小题,满分40分)
1.如图,已知公路l上A,B两点之间的距离为20m,已知B在C的南偏西30°的方向上,A在C的南偏西60°方向上,则点C到公路l的距离为( )
A.10m
B.m
C.10m
D.(10+10)m
2.如图,小明在C处看到西北方向上有一凉亭A,北偏东35°的方向上有一棵大树B,已知凉亭A在大树B的正西方向,若BC=100米,则A、B两点相距( )米.
A.100(cos35°+sin35°)
B.100(cos35°﹣sin35°)
C.(+)
D.(﹣)
3.如图为东西流向且河岸平行的一段河道,点A,B分别为两岸上一点,且点B在点A正北方向,由点A向正东方向走a米到达点C,此时测得点B在点C的北偏西55°方向上,则河宽AB的长为( )
A.atan55°米
B.米
C.米
D.米
4.如图,一艘海轮位于灯塔P的南偏东37°方向,距离灯塔40海里的A处,它沿正北方向航行一段时间后,到达位于灯塔的正东方向上的B处,这时,B处与灯塔P的距离PB的长可以表示为( )
A.40海里
B.40sin37°海里
C.40cos37°海里
D.40tan37°海里
5.如图,一艘轮船在A处测的灯塔C在北偏西15°的方向上,该轮船又从A处向正东方向行驶20海里到达B处,测的灯塔C在北偏西60°的方向上,则轮船在B处时与灯塔C之间的距离(即BC的长)为( )
A.40海里
B.(20+10)海里
C.40海里
D.(10+10)海里
6.如图,一渔船以32海里/时的速度向正北航行,在A处看到灯塔S在渔船的北偏东30°,半小时后航行到B处看到灯塔S在船的北偏东60°,若渔船继续向正北航行到C处时,此时渔船在灯塔S的正西方向,此时灯塔S与渔船的距离( )
A.16海里
B.18海里
C.8海里
D.8海里
7.如图,在A处测得点P在北偏东60°方向上,在B处测得点P在北偏东30°方向上,若AP=6千米,则A,B两点的距离为( )千米.
A.4
B.4
C.2
D.6
8.如图,某社会实践活动小组实地测量两岸互相平行的一段河的宽度,在河的南岸点A处,测得河的北岸边点B在其北偏东45°方向,然后向西走60米到达C点,测得点B在点C的北偏东60°方向,则这段河的宽度为( )
A.60()米
B.30()米
C.(90﹣30)米
D.30(﹣1)米
9.如图,一艘轮船从位于灯塔C的北偏东60°方向,距离灯塔60海里的小岛A出发,沿正南方向航行一段时间后,到达位于灯塔C的南偏东45°方向上的B处,这时轮船B与小岛A的距离是( )
A.30海里
B.60海里
C.120海里
D.(30+30)海里
10.如图,港口A在观测站O的正东方向,OA=6km,某船从港口A出发,沿北偏东15°方向航行一段距离后到达B处,此时从观测站O处测得该船位于北偏东60°的方向,则该船航行的距离(即AB的长)为( )
A.3km
B.3km
C.4
km
D.(3﹣3)km
二.填空题(共5小题,满分20分)
11.某数学小组三名同学运用自己所学的知识检测车速,他们将观测点设在一段笔直的公路旁且距公路100米的点A处,如图所示,直线l表示公路,一辆小汽车由公路上的B处向C处匀速行驶,用时5秒,经测量,点B在点A北偏东45°方向上,点C在点A北偏东60°方向上,这段公路最高限速60千米/小时,此车
(填“超速”或“没有超速”)(参考数据:≈1.732)
12.如图,在东西方向的海岸线上有A、B两个港口,甲货船从A港沿北偏东60°的方向以4海里/小时的速度出发,同时乙货船从B港沿西北方向出发,2小时后相遇在点P处,问乙货船每小时航行
海里.
13.如图,在某监测点B处望见一艘正在作业的渔船在南偏西15°方向的A处,若渔船沿北偏西75°方向以60海里/小时的速度航行,航行半小时后到达C处,在C处观测到B在C的北偏东60°方向上,则B、C之间的距离为
海里.
14.如图,为了测量河宽CD,先在A处测得对岸C点在其北偏东30°方向,然后沿河岸直行100米到点B,在B点测得对岸C点在其北偏西45°方向,则河宽CD是
米.(结果保留根号)
15.如图,一艘货轮以20海里/时的速度在海面上航行,当它行驶到A处时,发现它的东北方向有一灯塔B.货轮继续向北航行1小时后到达C处,发现灯塔B在它北偏东75°方向,那么此时货轮与灯塔B的距离为
海里(结果不取近似值).
三.解答题(共6小题,满分60分)
16.某景区A、B两个景点位于湖泊两侧,游客从景点A到景点B必须经过C处才能到达.观测得景点B在景点A的北偏东30°,从景点A出发向正北方向步行600米到达C处,测得景点B在C的北偏东75°方向.
(1)求景点B和C处之间的距离;(结果保留根号)
(2)当地政府为了便捷游客游览,打算修建一条从景点A到景点B的笔直的跨湖大桥.大桥修建后,从景点A到景点B比原来少走多少米?(结果保留整数.参考数据:≈1.414,≈1.732)
17.在一次海上救援中,两艘专业救助船A、B同时收到某事故渔船P的求救讯息,已知此时救助船B在A的正北方向,事故渔船P在救助船A的北偏西30°方向上,在救助船B的西南方向上,且事故渔船P与救助船A相距120海里.
(1)求收到求救讯息时事故渔船P与救助船B之间的距离(结果保留根号);
(2)求救助船A、B分别以40海里/小时,30海里/小时的速度同时出发,匀速直线前往事故渔船P处搜救,试通过计算判断哪艘船先到达.
18.小明周末与父母一起到遂宁湿地公园进行数学实践活动,在A处看到B、C处各有一棵被湖水隔开的银杏树,他在A处测得B在北偏西45°方向,C在北偏东30°方向,他从A处走了20米到达B处,又在B处测得C在北偏东60°方向.
(1)求∠C的度数;
(2)求两棵银杏树B、C之间的距离(结果保留根号).
19.如图,A,B是海面上位于东西方向的两个观测点,有一艘海轮在C点处遇险发出求救信号,此时测得C点位于观测点A的北偏东45°方向上,同时位于观测点B的北偏西60°方向上,且测得C点与观测点A的距离为25海里.
(1)求观测点B与C点之间的距离;
(2)有一艘救援船位于观测点B的正南方向且与观测点B相距30海里的D点处,在接到海轮的求救信号后立即前往营救,其航行速度为42海里/小时,求救援船到达C点需要的最少时间.
20.为了维护国家主权和海洋权力,海监部门对我国领海实现了常态化巡航管理.如图所示,正在执行巡航任务的海监船以每小时40海里的速度向正东方向航行,在A处测得灯塔P在北偏东60°方向上,继续航行30分钟后到达B处,此时测得灯塔P在北偏东45°方向上.
(1)求∠APB的度数;
(2)已知在灯塔P的周围25海里内有暗礁,问海监船继续向正东方向航行是否安全?(参考数据:≈1.414,≈1.732)
21.因东坡文化远近闻名的遗爱湖公园,“国庆黄金周”期间,游人络绎不绝,现有一艘游船载着游客在遗爱湖中游览,当船在A处时,船上游客发现岸上P1处的临摹亭和P2处的遗爱亭都在东北方向,当游船向正东方向行驶600m到达B处时,游客发现遗爱亭在北偏西15°方向,当游船继续向正东方向行驶400m到达C处时,游客发现临摹亭在北偏西60°方向.
(1)求A处到临摹亭P1处的距离;
(2)求临摹亭P1处与遗爱亭P2处之间的距离.(计算结果保留根号)
参考答案
一.选择题(共10小题,满分40分)
1.解:如图,过点C作CD⊥直线l于点D,
∴∠ADC=90°,
∵∠BCD=30°,∠ACD=60°,AB=20m,
∴∠ACB=∠ACD﹣∠BCD=60°﹣30°=30°,∠CAD=90°﹣∠ACD=90°﹣60°=30°,∠CBD=90°﹣∠BCD=90°﹣30°=60°,
∴∠ACB=∠CAD,
∴AB=BC=20m,
在Rt△BCD中,
∵sin∠CBD=,
∴CD=BC sin∠CBD=20×=10(m),
故选:C.
2.解:过点C作AB的垂线交AB于D,
∵B点在A点的正东方向上,
∴∠ACD=45°,∠DCB=35°,
在Rt△BCD中,BC=100,
∴DB=BCsin35°=100 sin35°(米),
CD=BCcos35°=100 cos35°(米),
在Rt△ACD中,AD=CD,
∴AB=AD+DB=100(sin35°+cos35°)(米).
故选:A.
3.解:连接AB,BC,
由题意得,∠BAC=90°,∠ABC=55°,AC=a米,
∴tan∠ABC=tan55°=,
∴AB==,
故选:D.
4.解:∵一艘海轮位于灯塔P的南偏东37°方向,
∴∠BAP=37°,
∵AP=40海里,
∴BP=AP sin37°=40sin37°海里;
故选:B.
5.解:过A作AD⊥BC于D,如图所示:
在Rt△ABD中,∠ABD=90°﹣60°=30°,AB=20海里,
∴AD=AB=10(海里),BD=AD=AB=10(海里),
∵∠ABC=90°﹣60°=30°,∠BAC=90°+15°=105°,
∴∠C=180°﹣105°﹣30°=45°,
∴△ACD是等腰直角三角形,
∴CD=AD=10(海里),
∴BC=BD+CD=(10+10)海里,
故选:D.
6.解:由题意得,AB=32×=16(海里),∠ACS=90°,
∵∠A=30°,∠CBS=60°,
∴∠ASB=∠CBS﹣∠A=30°,
∴∠ASB=∠A,
∴BS=AB=16(海里),
在Rt△CBS中,sin∠CBS=,
∴CS=BS sin∠CBS=16×=8(海里),
故选:D.
7.解:由题意知,∠PAB=30°,∠PBC=60°,
∴∠APB=∠PBC﹣∠PAB=60°﹣30°=30°,
∴∠PAB=∠APB,
∴AB=PB,
在Rt△PAC中,∵AP=6千米,
∴PC=PA=3千米,
在Rt△PBC中,∵sin∠PBC=,
∴PB===6千米.
故选:D.
8.解:作BD⊥CA交CA的延长线于D,
设BD=xm,
∵∠BCA=30°,
∴CD==x,
∵∠BAD=45°,
∴AD=BD=x,
则x﹣x=60,
解得x==30(),
答:这段河的宽约为30()米.
故选:B.
9.解:过C作CD⊥AB于D,
∴∠ACD=30°,∠BCD=45°,AC=60海里,
在Rt△ACD中,AD=AC=30(海里),cos∠ACD=,
∴CD=AC cos∠ACD=60×=30(海里),
在Rt△DCB中,∵∠BCD=∠B=45°,
∴CD=BD=30(海里),
∴AB=AD+BD=(30+30)海里,
答:这时轮船B与小岛A的距离是(30+30)海里.
故选:D.
10.解:作AC⊥OB于点C,如右图所示,
由已知可得,
∠COA=30°,OA=6km,
∵AC⊥OB,
∴∠OCA=∠BCA=90°,
∴OA=2AC,∠OAC=60°,
∴AC=3km,∠CAD=30°,
∵∠DAB=15°,
∴∠CAB=45°,
∴∠CAB=∠B=45°,
∴BC=AC,
∴AB=,
故选:A.
二.填空题(共5小题,满分20分)
11.解:作AD⊥直线l于D,
在Rt△ADB中,∠ABD=45°,
∴BD=AD=100,
在Rt△ADB中,tan∠ACD=,
则CD==100≈173.2,
∴BC=173.2﹣100=73.2(米),
小汽车的速度为:0.0732÷=52.704(千米/小时),
∵52.704千米/小时<60千米/小时,
∴小汽车没有超速,
故答案为:没有超速.
12.解:作PC⊥AB于点C,
∵甲货船从A港沿北偏东60°的方向以4海里/小时的速度出发,
∴∠PAC=30°,AP=4×2=8,
∴PC=AP×sin30°=8×=4.
∵乙货船从B港沿西北方向出发,
∴∠PBC=45°,
∴PB=PC÷=4,
∴乙货船每小时航行4÷2=2海里/小时,
故答案为2.
13.解:由题意得,AC=60×0.5=30海里,
∵CD∥BF,
∴∠CBF=∠DCB=60°,又∠ABF=15°,
∴∠ABC=45°,
∵AE∥BF,
∴∠EAB=∠FBA=15°,又∠EAC=75°,
∴∠CAB=90°,
∴BC=AC=30海里,
故答案为:30.
14.解:设CD=x米,
由题意得:CD⊥AB,∠ACD=30°,∠BCD=45°,
∴∠ADC=∠BDC=90°,
∴AD=CD=x米,BD=CD=x米,
∵AD+BD=AB=100米,
∴x+x=100,
解得:x=150﹣50,
即河宽CD是(150﹣50)米,
故答案为:(150﹣50).
15.解:作CE⊥AB于E,
20海里/时×1小时=20海里,
∴AC=20海里,
∵∠A=45°,
∴CE=AC sin45°=10,
∵∠NCB=75°,∠A=45°,
∴∠B=30°,
∴BC===20海里,
故答案为:20.
三.解答题(共6小题,满分60分)
16.解:(1)过点C作CD⊥AB于点D,
由题意得,∠A=30°,∠BCE=75°,AC=600m,
在Rt△ACD中,∠A=30°,AC=600,
∴CD=AC=300(m),
AD=AC=300(m),
∵∠BCE=75°=∠A+∠B,
∴∠B=75°﹣∠A=45°,
∴CD=BD=300(m),
BC=CD=300(m),
答:景点B和C处之间的距离为300m;
(2)由题意得.
AC+BC=(600+300)m,
AB=AD+BD=(300+300)m,
AC+BC﹣AB=(600+300)﹣(300+300)
≈204.6
≈205(m),
答:大桥修建后,从景点A到景点B比原来少走约205m.
17.解:(1)作PC⊥AB于C,如图所示:
则∠PCA=∠PCB=90°,
由题意得:PA=120海里,∠A=30°,∠CBP=45°,
在Rt△ACP中,∵∠CAP=30°,∠PCA=90°,
∴PC=PA=60海里,
在Rt△BCP中,∵∠PCB=90°,∠CBP=45°,sin∠CBP=,
∴PB===60(海里),
答:收到求救讯息时事故渔船P与救助船B之间的距离为60海里;
(2)∵PA=120海里,PB=60海里,救助船A,B分别以40海里/小时、30海里/小时的速度同时出发,
∴救助船A所用的时间为=3(小时),救助船B所用的时间为=2(小时),
∵3>2,
∴救助船B先到达.
18.解:(1)设AD与BC交于点F,
由题意得BE∥AD,
∵BE∥AD且∠EBF=60°,
∴∠BFA=∠EBF=60°,
∵∠BFA=∠C+∠CAD且∠CAD=30°,
∴∠C=∠BFA﹣∠CAD=30°;
(2)过点B作BG⊥AD于G.
∵BG⊥AD,
∴∠AGB=∠BGD=90°,
在Rt△AGB中,AB=20米,∠BAG=45°,
AG=BG=20×sin45°=(米),
在Rt△BGF中,∠BFG=60°,
∴BF=BGsin60°=(米),FG=BGtan60°=(米),
∵∠C=∠CAD=30°,
∴CF=AF=AG+FG=(10+)(米),
∴BC=BF+CF=(10+10)米,
答:两棵银杏树B、C之间的距离为
()米.
19.解:(1)如图,过点C作CE⊥AB于点E,
根据题意可知:∠ACE=∠CAE=45°,AC=25海里,
∴AE=CE=25(海里),
∵∠CBE=30°,
∴BE=25(海里),
∴BC=2CE=50(海里).
答:观测点B与C点之间的距离为50海里;
(2)如图,作CF⊥DB于点F,
∵CF⊥DB,FB⊥EB,CE⊥AB,
∴四边形CEBF是矩形,
∴FB=CE=25(海里),CF=BE=25(海里),
∴DF=BD+BF=30+25=55(海里),
在Rt△DCF中,根据勾股定理,得
CD===70(海里),
∴70÷42=(小时).
答:救援船到达C点需要的最少时间是小时.
20.解:(1)由题意得,∠PAB=90°﹣60°=30°,∠ABP=90°+45°=135°,
∴∠APB=180°﹣∠PAB﹣∠ABP=180°﹣30°﹣135°=15°;
(2)海监船继续向正东方向航行安全,理由如下:
作PH⊥AB于H,如图:
则△PBH是等腰直角三角形,
∴BH=PH,
设BH=PH=x海里,
由题意得:AB=40×=20(海里),
在Rt△APH中,tan∠PAB=tan30°==,
即=,
解得:x=10+10≈27.32>25,且符合题意,
∴海监船继续向正东方向航行安全.
21.解:(1)作P1M⊥AC于M,
设P1M=xm,
在Rt△P1AM中,∵∠P1AB=45°,
∴AM=P1M=xm,
在Rt△P1CM中,∵∠P1CA=30°,
∴MC==xm,
∵AC=1000
m,
∴x+=1000,解得x=500(﹣1)(m),
∴P1M=500(﹣1)m
∴P1A==500(﹣)m,
故A处到临摹亭P1处的距离为500(﹣)m;
(2)作BN⊥AP2于N,
∵∠P2AB=45°,∠P2BA=75°,
∴∠P2=60°,
在Rt△ABN中,∵∠P1AB=45°,AB=600
m
∴BN=AN=AB=300
m,
∴P1N=500(﹣)﹣300=(500﹣800)
(m),
在Rt△P2BN中,∵∠P2=60°,
∴P2N=BN=×=100
(m),
∴P1P2=100﹣(500﹣800)=(800﹣400)
(m).
故临摹亭P1处与遗爱亭P2处之间的距离是(800﹣400)m.
