2.4解直角三角形同步能力提升训练 2021-2022学年九年级数学鲁教版(五四制)上册(word版含答案)
文档属性
| 名称 | 2.4解直角三角形同步能力提升训练 2021-2022学年九年级数学鲁教版(五四制)上册(word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 559.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-05 08:36:32 | ||
图片预览


文档简介
2021-2022学年鲁教版九年级数学上册《2.4解直角三角形》同步能力提升训练(附答案)
一、选择题
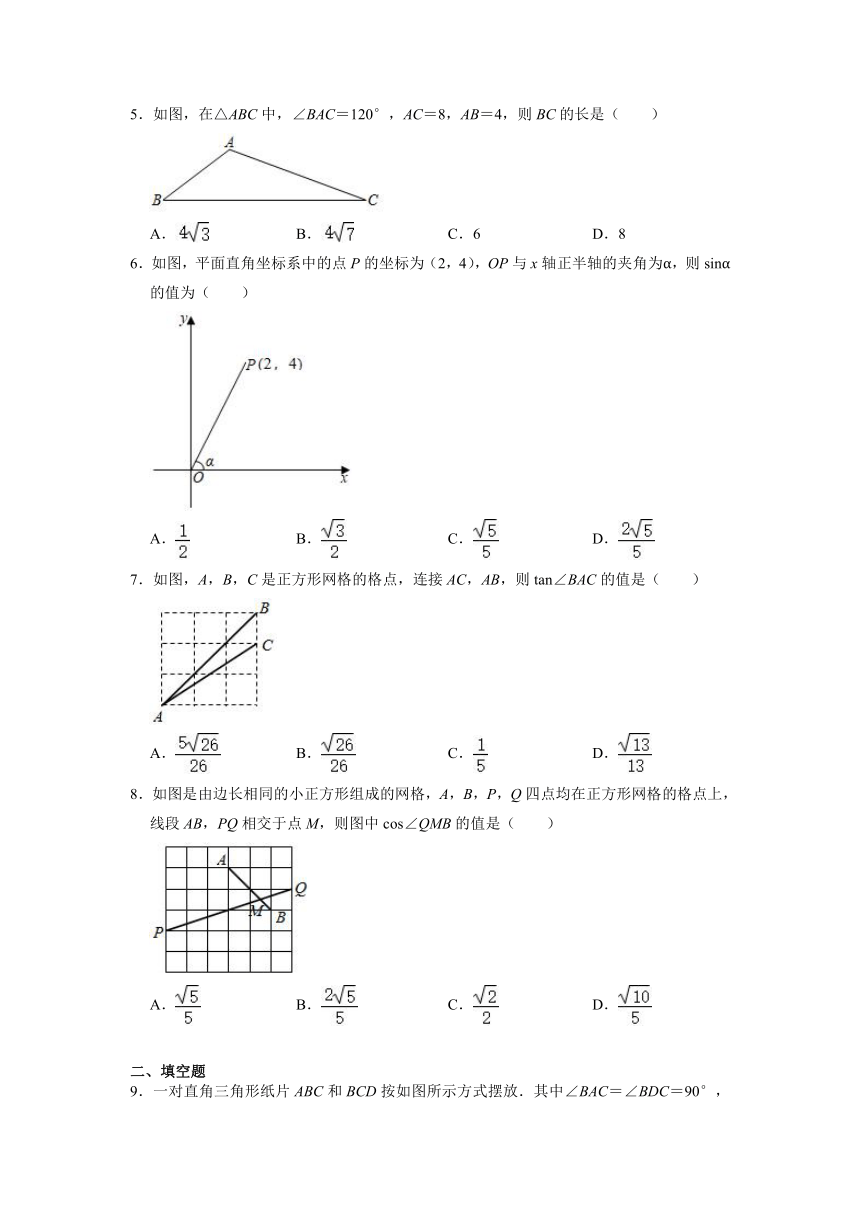
1.如图,Rt△ABC中,∠ABC=90°,AB=6,BC=8,D为AC边上一动点,且tan∠ABD=,则BD的长度为( )
A.
B.2
C.5
D.
2.如图,在△ABC中,AD⊥BC于D,如果BD=9,DC=5,cosB=,E为AC的中点,那么sin∠EDC的值为( )
A.
B.
C.
D.
3.如图,在Rt△ABC中∠C=90°,直线MN垂直平分AB交AB于M,交BC于N,且∠B=15°,AC=3,则BC的长为( )
A.6
B.6+3
C.6+2
D.9
4.如图,A,B,C是小正方形的顶点,每个小正方形的边长为a,则sin∠BAC的值为( )
A.
B.1
C.
D.
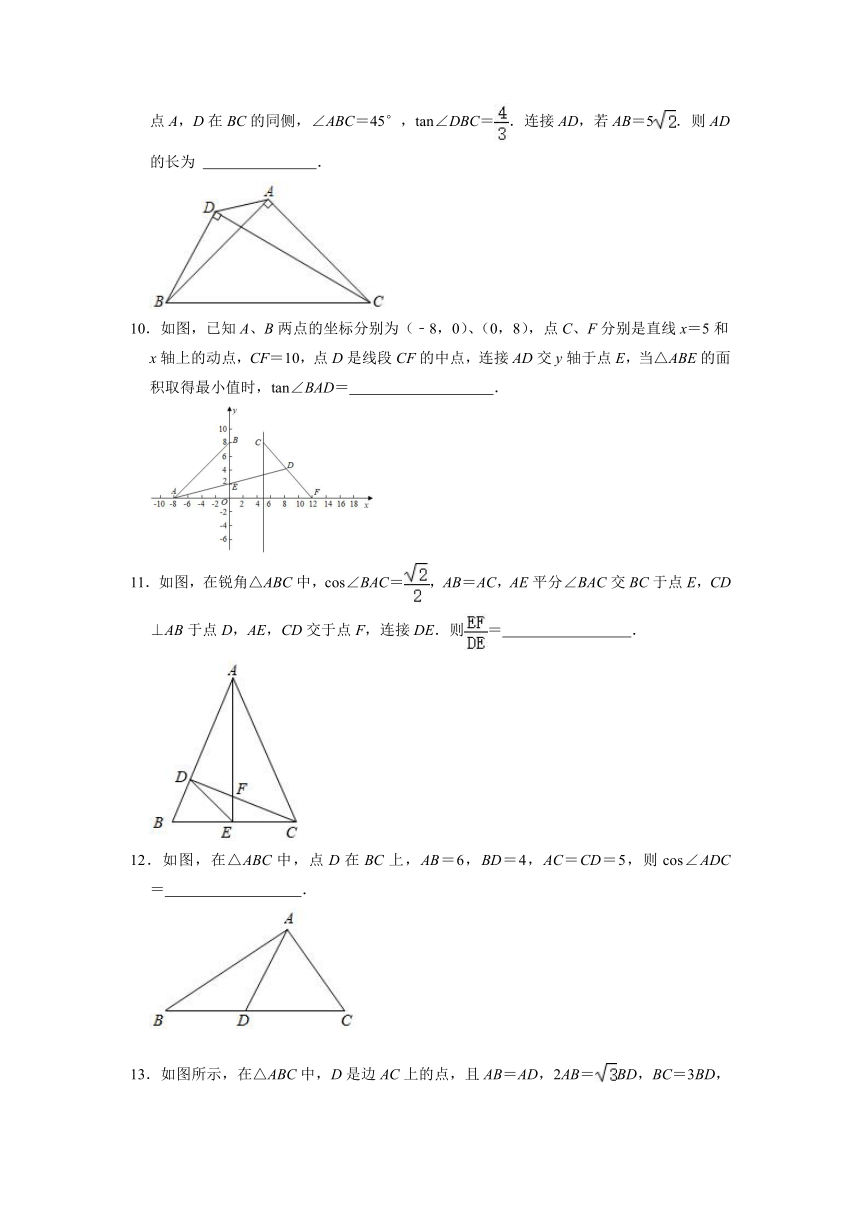
5.如图,在△ABC中,∠BAC=120°,AC=8,AB=4,则BC的长是( )
A.
B.
C.6
D.8
6.如图,平面直角坐标系中的点P的坐标为(2,4),OP与x轴正半轴的夹角为α,则sinα的值为( )
A.
B.
C.
D.
7.如图,A,B,C是正方形网格的格点,连接AC,AB,则tan∠BAC的值是( )
A.
B.
C.
D.
8.如图是由边长相同的小正方形组成的网格,A,B,P,Q四点均在正方形网格的格点上,线段AB,PQ相交于点M,则图中cos∠QMB的值是( )
A.
B.
C.
D.
二、填空题
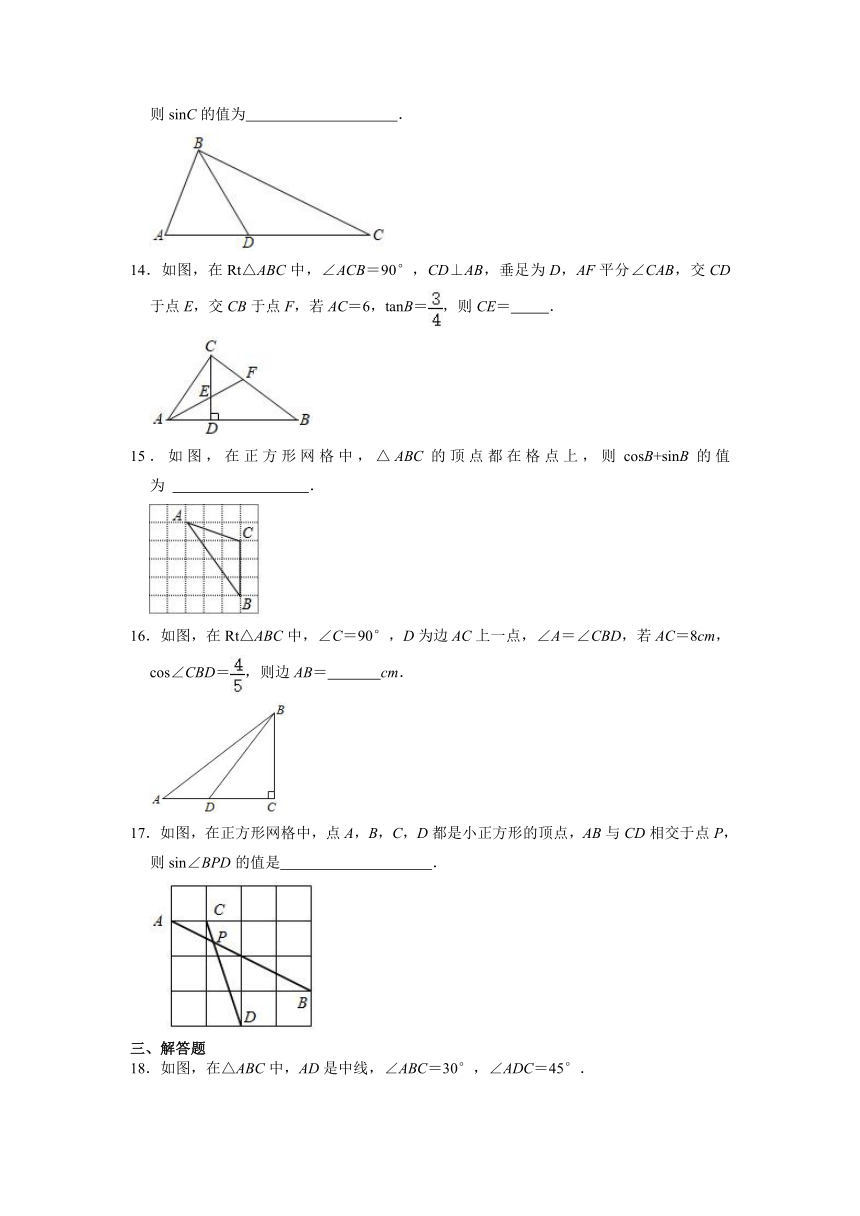
9.一对直角三角形纸片ABC和BCD按如图所示方式摆放.其中∠BAC=∠BDC=90°,点A,D在BC的同侧,∠ABC=45°,tan∠DBC=.连接AD,若AB=5.则AD的长为
.
10.如图,已知A、B两点的坐标分别为(﹣8,0)、(0,8),点C、F分别是直线x=5和x轴上的动点,CF=10,点D是线段CF的中点,连接AD交y轴于点E,当△ABE的面积取得最小值时,tan∠BAD=
.
11.如图,在锐角△ABC中,cos∠BAC=,AB=AC,AE平分∠BAC交BC于点E,CD⊥AB于点D,AE,CD交于点F,连接DE.则=
.
12.如图,在△ABC中,点D在BC上,AB=6,BD=4,AC=CD=5,则cos∠ADC=
.
13.如图所示,在△ABC中,D是边AC上的点,且AB=AD,2AB=BD,BC=3BD,则sinC的值为
.
14.如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D,AF平分∠CAB,交CD于点E,交CB于点F,若AC=6,tanB=,则CE=
.
15.如图,在正方形网格中,△ABC的顶点都在格点上,则cosB+sinB的值为
.
16.如图,在Rt△ABC中,∠C=90°,D为边AC上一点,∠A=∠CBD,若AC=8cm,cos∠CBD=,则边AB=
cm.
17.如图,在正方形网格中,点A,B,C,D都是小正方形的顶点,AB与CD相交于点P,则sin∠BPD的值是
.
三、解答题
18.如图,在△ABC中,AD是中线,∠ABC=30°,∠ADC=45°.
(1)求的值;
(2)求∠ACB的度数.
19.如图在等腰三角形ABC中,AB=AC,点D、E分别是AB、BC的中点,过点B作BF⊥AC于点F,BF与DE交于点G.
(1)求证:DE⊥BF;
(2)连结EF,若S△CEF=S△BDG,求cos∠CEF的值.
20.如图,在Rt△ABC中,∠C=90°,D为BC的中点,AB=5,AC=3.
(1)求AD的长;
(2)求sin∠DAB的值.
21.如图,A、B、D三点在同一水平线上,CD⊥AD,∠A=45°,∠CBD=75°,AB=60m.
(1)求∠ACB的度数;
(2)求线段CB的长度.
22.将一副直角三角板如图所示放置,点C,D,F在同一直线上,AB∥CF,∠ACB=∠F=90°,∠A=60°,∠E=45°,若AB=20,求CD的长.
23.如图,在Rt△ABC中,∠A=90°,作BC的垂直平分线交AC于点D,延长AC至点E,使CE=AB.
(1)若AE=1,求△ABD的周长;
(2)若AD=BD,求tan∠ABC的值.
24.如图,已知△ABD中,AC⊥BD,BC=8,CD=4,cos∠ABC=,BF为AD边上的中线.
(1)求AC的长;
(2)求tan∠FBD的值.
参考答案
1.解:作DE⊥AB于点E,
设DE长为x,则tanA===,
∴EA=x,
∵tan∠ABD==,
∴BE=2x,
∴AB=EA+BE=x+2x=6,
∴x=,
∴BD===,
故选:D.
2.解:在Rt△ABD中,cosB==,BD=9,
∴AB=BD=15,
由勾股定理得AD===12,
在Rt△ADC中,由勾股定理得AC===13,
∵E为AC中点,
∴ED=EC=AC=,
∴sin∠EDC=sinC==.
故选:C.
3.解:如图,连接AN.
∵MN垂直平分线段AB,
∴NA=NB,
∴∠B=∠BAN=15°,
∴∠ANC=∠B+∠NAB=30°,
∵AC=3,∠C=90°,
∴AN=2AC=6,CN===3,
∴BC=CN+BN=3+6,
故选:B.
4.解:过点B作BD⊥AC,垂足为D,
由题意可得,
∵S长方形EFGC=2a×3a=6a2,S△AEC===,S△AFB===a2,
S△CBG===a2,
∴S△ABC=S长方形EFGC﹣S△AEC﹣S△AFB﹣S△BGC=6a2﹣﹣a2﹣a2=,
在Rt△AEC中,
AC===,
∵S△ABC===,
解得BD=a,
在Rt△AFB中,
AB===,
在Rt△ABD中,
sin∠BAC===.
故选:C.
5.解:如图,过点C作CE⊥BA交BA的延长线于E.
∵∠BAC=120°,
∴∠CAE=180°﹣120°=60°,
∴AE=AC cos60°=4,EC=AC sin60°=4,
∵AB=4,
∴BE=AB+AE=8,
∴BC===4,
故选:B.
6.解:如图,过点P作PH⊥x轴于H.
∵P(2,4),
∴OH=2,PH=4,
∴OP===2,
∴sinα===,
故选:D.
7.解:如图,作CE⊥AB于E,
设小正方形边长为1,则易证△BEC是等腰直角三角形,
∴CE=BE=,AB==3,
∴AE=AB﹣BE==3﹣=,
在Rt△AEC中,tan∠EAC===.
∴tan∠BAC的值是,
故选:C.
8.解:作CQ∥AB,连接PC,如右图所示,
设每个小正方形的边长为1,
则CQ==2,PQ==2,PC==4,
∴CQ2+PC2=(2)2+(4)2=8+32=40=(2)2=PQ2,
∴△PCQ是直角三角形,∠PCQ=90°,
∴cos∠PQC===,
∵AB∥CQ,
∴∠QMB=∠PQC,
∴cos∠QMB的值是,
故选:A.
9.解:如图,分别过点A、D作AF⊥BC、DE⊥BC,交BC于点F、E,过点D作DM⊥AF,于点M,
在Rt△ABC中,
∵AB=5,∠ABC=45°,
∴AC=AB=5,BC=10,
∴AF=BF=5,
在Rt△BCD中,
∵tan∠DBC=,
∴BD=6,
在Rt△BDE中,
∵tan∠DBE=,
∴DE=,BE=,
∵∠DEF=∠DMF=∠EFM=90°,
∴四边形DEFM是矩形,
∴DM=EF=BF﹣BE=,MF=DE=,
∴AM=AF﹣MF=,
在Rt△ADM中,由勾股定理,得:AD==,
故答案为:.
10.解:如图,设直线x=﹣5交x轴于K,连接DK,由题意KD=CF=5,
∴点D的运动轨迹是以K为圆心,5为半径的圆,
∴当直线AD与⊙K相切时,△ABE的面积最小,
∵AD是切线,点D是切点,
∴AD⊥KD,
∵AK=13,DK=5,
∴AD=12,
∵tan∠EAO==,
∴=,
∴OE=,
∴AE==,
作EH⊥AB于H.
∵S△ABE= AB EH=S△AOB﹣S△AOE,
∴EH=,
∴AH==,
∴tan∠BAD===.
11.解:如图,在AE上取一点M,使得AM=MC.设EC=m.
∵cos∠BAC=,
∴∠BAC=45°,
∵AB=AC,AE平分∠BAC,
∴AE⊥BC,∠EAC=∠BAC=22.5°,
∵MA=MC,
∴∠MAC=∠MCA=22.5°,
∴∠CME=∠MAC+∠MCA=45°,
∴EC=EM=m,AM=CM=m,AE=m+m,
∵∠ADC=∠AEC=90°,
∴A,D,E,C四点共圆,
∴∠ECF=∠DAE=22.5°,
∵∠DAE=∠EAC,
∴=,
∴DE=ED,
∴===tan22.5°==﹣1.
故答案为:﹣1
12.解:如图:过点A作AE⊥BC,交BC于点E,
设DE=x,则CE=5﹣x,
在Rt△ABE中,AE2=AB2﹣BE2,
则AE2=62﹣(4﹣x)2①,
在Rt△ACE中,AE2=AC2﹣CE2,
则AE2=52﹣(5﹣x)2②,
由①②得,62﹣(4﹣x)2=52﹣(5﹣x)2,
解得:x=,则DE=,
在Rt△ADE中,AD2=AE2+DE2③,
将x=代入①式,得AE=,
则AD2=()2+()2,
解得AD=,
∴cos∠ADC==.
13.解:设BD=a,则由题意可得:BC=3a,AB=AD=a,
在△ABD中,由余弦定理得:cosA===,
∴sinA==,
在△ABC中,由正弦定理得,=,
即=,
解得:sinC=,
故答案为:.
14.解:过点F作FG⊥AB于点G,
∵∠ACB=90°,CD⊥AB,
∴∠CDA=90°,
∴∠CAF+∠CFA=90°,∠FAD+∠AED=90°,
∵AF平分∠CAB,
∴∠CAF=∠FAD,
∴∠CFA=∠AED=∠CEF,
∴CE=CF,
∵AF平分∠CAB,∠ACF=∠AGF=90°,
∴FC=FG,
∵∠B=∠B,∠FGB=∠ACB=90°,
∴△BFG∽△BAC,
∴=,
∵AC=6,∠ACB=90°,
∴tanB==
∴BC=8,AB===10,
∴=,
∵FC=FG,
解得:FC=3,
即CE的长为3.
故答案为:3.
15.解:如图,过点A作AE⊥BC交BC的延长线于E.
在Rt△ABE中,∠E=90°,AE=3,BE=4,
∴AB===5,
∴cosB==,sinB==,
∴cosB+sinB=+=,
故答案为:.
16.解:∵∠C=90°,∠A=∠CBD,cos∠CBD=,
∴cos∠A==,
∵AC=8cm,
∴AB=10cm.
故答案为:10.
17.解:如图所示:连接AE、BE.
∵AC=ED=1,AC∥ED,
∴四边形AEDC是平行四边形.
∴AE∥CD.
∴∠EAB=∠DPB.
∵BE=AE==,
AB===2.
∴AB2=AE2+BE2.
∴△AEB是等腰直角三角形.
∴∠EAB=∠DPB=45°.
∴sin∠BPD=sin45°=.
故答案为:.
18.解:(1)过点A作BD的垂线交BD的延长线于点E,
在Rt△ABE中,
∵∠ABC=30°,
∴AB=2AE,
BE==AE,
在Rt△ADE中,
∵∠ADC=45°,
∴DE=AE,
∴BD=BE﹣DE=AE﹣AE=(﹣1)AE,
∴==+1;
(2)如图,在AB上取一点E,使得DB=DE,连接EC.
∵DB=DE,
∴∠DBE=∠DEB=30°,
∴∠EDC=∠B+∠DEB=60°,
∵DB=DC=DE,
∴△DEC是等边三角形,
∴∠ECD=∠CED=60°,
∴∠CEB=∠CEA=90°,
∵∠ADC=45°,
∴∠EDA=∠EDC﹣∠ADC=15°,
∵∠DEB=∠EDA+∠AED,
∴∠EDA=∠EAD=15°,
∴ED=EA=EC,
∵∠CEA=90°,
∴∠ECA=45°,
∴∠ACB=∠ACE+∠ECB=45°+60°=105°.
19.证明:(1)∵点D、E分别是AB、BC的中点,
∴DE是△ABC的中位线,
∴DE∥AC.
∴∠DGB=∠AFB.
∵BF⊥AC,
∴∠AFB=∠BFC=90°.
∴∠DGB=90°,
∴DE⊥BF.
(2)∵∠BFC=90°,点E是BC的中点,
∴EF=BE=EC,
∴∠EFC=∠C.
∵AB=AC,
∴∠ABC=∠C.
∴∠CEF=180°﹣2∠C=∠BAC.
∵DE∥AC,点D是AB的中点,
∴△BDG∽△BAF,
∴=.
∵点E是BC的中点,
∴S△BFC=2S△CEF,
∵S△CEF=,
∴.
∴S△AFB=S△ABF+S△BCF=S△ABF+2S△CEF=S△CEF.
∴==S△CEF:S△CEF=,
在Rt△ABF中,cos∠CEF=cos∠BAF===.
20.解:(1)∵∠C=90°,AB=5,AC=3,
∴BC=
==
4.
∵D是BC的中点,
∴CD=BC=2.
∴AD=
=
=.
(2)过点D作DE⊥AB,垂足为E.
∵D为BC的中点,
∴S△ACD=S△ADB=AC×CD=3.
∵S△ABD=AB×DE=3,
∴DE=.
∴sin∠DAB=
=
=.
21.解:(1)∵∠CBD=∠A+∠ACB,∠A=45°,∠CBD=75°,
∴∠ACB=75°﹣45°=30°.
(2)如图,过点B作BH⊥AC于H.
∵∠BHA=90°,AB=60m,∠A=45°,
∴BH=AB sin45°=60(m),
∵∠BCH=30°,
∴BC=2BH=120(m).
22.解:(1)如图,作BH⊥CF于点H,
在Rt△ABC中,∠ACB=90°,∠A=60°,
∴∠ABC=30°,
∵AB∥CF,
∴∠BCH=∠ABC=30°,
∵AB=20,
∴,
在Rt△BCH中,∵∠BCH=30°,
∴,CH=BC×cos30°=15,
在Rt△DEF中,∵∠E=45°,
∴∠EDF=∠E=45°,
在Rt△BDH中,,
∴.
23.解:(1)如图,连接BD,设BC垂直平分线交BC于点F,
∴BD=CD,
C△ABD=AB+AD+BD
=AB+AD+DC
=AB+AC,
∵AB=CE,
∴C△ABD=AC+CE=AE=1,
故△ABD的周长为1.
(2)设AD=x,
∴BD=3x,
又∵BD=CD,
∴AC=AD+CD=4x,
在Rt△ABD中,AB===2.
∴tan∠ABC===.
24.解:(1)∵AC⊥BD,cos∠ABC==,BC=8,
∴AB=10,
在Rt△ACB中,由勾股定理得,
AC===6,
即AC的长为6;
(2)如图,
连接CF,过F点作BD的垂线,垂足E,
∵BF为AD边上的中线,
即F为AD的中点,
∴CF=AD=FD,
在Rt△ACD中,由勾股定理得,
AD===2,
∵三角形CFD为等腰三角形,FE⊥CD,
∴CE=CD=2,
在Rt△EFC中,EF===3,
∴tan∠FBD===.
解法二:∵BF为AD边上的中线,
∴F是AD中点,
∵FE⊥BD,AC⊥BD,
∴FE∥AC,
∴FE是△ACD的中位线,
∴FE=AC=3,CE=CD=2,
∴在Rt△BFE中,tan∠FBD===
一、选择题
1.如图,Rt△ABC中,∠ABC=90°,AB=6,BC=8,D为AC边上一动点,且tan∠ABD=,则BD的长度为( )
A.
B.2
C.5
D.
2.如图,在△ABC中,AD⊥BC于D,如果BD=9,DC=5,cosB=,E为AC的中点,那么sin∠EDC的值为( )
A.
B.
C.
D.
3.如图,在Rt△ABC中∠C=90°,直线MN垂直平分AB交AB于M,交BC于N,且∠B=15°,AC=3,则BC的长为( )
A.6
B.6+3
C.6+2
D.9
4.如图,A,B,C是小正方形的顶点,每个小正方形的边长为a,则sin∠BAC的值为( )
A.
B.1
C.
D.
5.如图,在△ABC中,∠BAC=120°,AC=8,AB=4,则BC的长是( )
A.
B.
C.6
D.8
6.如图,平面直角坐标系中的点P的坐标为(2,4),OP与x轴正半轴的夹角为α,则sinα的值为( )
A.
B.
C.
D.
7.如图,A,B,C是正方形网格的格点,连接AC,AB,则tan∠BAC的值是( )
A.
B.
C.
D.
8.如图是由边长相同的小正方形组成的网格,A,B,P,Q四点均在正方形网格的格点上,线段AB,PQ相交于点M,则图中cos∠QMB的值是( )
A.
B.
C.
D.
二、填空题
9.一对直角三角形纸片ABC和BCD按如图所示方式摆放.其中∠BAC=∠BDC=90°,点A,D在BC的同侧,∠ABC=45°,tan∠DBC=.连接AD,若AB=5.则AD的长为
.
10.如图,已知A、B两点的坐标分别为(﹣8,0)、(0,8),点C、F分别是直线x=5和x轴上的动点,CF=10,点D是线段CF的中点,连接AD交y轴于点E,当△ABE的面积取得最小值时,tan∠BAD=
.
11.如图,在锐角△ABC中,cos∠BAC=,AB=AC,AE平分∠BAC交BC于点E,CD⊥AB于点D,AE,CD交于点F,连接DE.则=
.
12.如图,在△ABC中,点D在BC上,AB=6,BD=4,AC=CD=5,则cos∠ADC=
.
13.如图所示,在△ABC中,D是边AC上的点,且AB=AD,2AB=BD,BC=3BD,则sinC的值为
.
14.如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D,AF平分∠CAB,交CD于点E,交CB于点F,若AC=6,tanB=,则CE=
.
15.如图,在正方形网格中,△ABC的顶点都在格点上,则cosB+sinB的值为
.
16.如图,在Rt△ABC中,∠C=90°,D为边AC上一点,∠A=∠CBD,若AC=8cm,cos∠CBD=,则边AB=
cm.
17.如图,在正方形网格中,点A,B,C,D都是小正方形的顶点,AB与CD相交于点P,则sin∠BPD的值是
.
三、解答题
18.如图,在△ABC中,AD是中线,∠ABC=30°,∠ADC=45°.
(1)求的值;
(2)求∠ACB的度数.
19.如图在等腰三角形ABC中,AB=AC,点D、E分别是AB、BC的中点,过点B作BF⊥AC于点F,BF与DE交于点G.
(1)求证:DE⊥BF;
(2)连结EF,若S△CEF=S△BDG,求cos∠CEF的值.
20.如图,在Rt△ABC中,∠C=90°,D为BC的中点,AB=5,AC=3.
(1)求AD的长;
(2)求sin∠DAB的值.
21.如图,A、B、D三点在同一水平线上,CD⊥AD,∠A=45°,∠CBD=75°,AB=60m.
(1)求∠ACB的度数;
(2)求线段CB的长度.
22.将一副直角三角板如图所示放置,点C,D,F在同一直线上,AB∥CF,∠ACB=∠F=90°,∠A=60°,∠E=45°,若AB=20,求CD的长.
23.如图,在Rt△ABC中,∠A=90°,作BC的垂直平分线交AC于点D,延长AC至点E,使CE=AB.
(1)若AE=1,求△ABD的周长;
(2)若AD=BD,求tan∠ABC的值.
24.如图,已知△ABD中,AC⊥BD,BC=8,CD=4,cos∠ABC=,BF为AD边上的中线.
(1)求AC的长;
(2)求tan∠FBD的值.
参考答案
1.解:作DE⊥AB于点E,
设DE长为x,则tanA===,
∴EA=x,
∵tan∠ABD==,
∴BE=2x,
∴AB=EA+BE=x+2x=6,
∴x=,
∴BD===,
故选:D.
2.解:在Rt△ABD中,cosB==,BD=9,
∴AB=BD=15,
由勾股定理得AD===12,
在Rt△ADC中,由勾股定理得AC===13,
∵E为AC中点,
∴ED=EC=AC=,
∴sin∠EDC=sinC==.
故选:C.
3.解:如图,连接AN.
∵MN垂直平分线段AB,
∴NA=NB,
∴∠B=∠BAN=15°,
∴∠ANC=∠B+∠NAB=30°,
∵AC=3,∠C=90°,
∴AN=2AC=6,CN===3,
∴BC=CN+BN=3+6,
故选:B.
4.解:过点B作BD⊥AC,垂足为D,
由题意可得,
∵S长方形EFGC=2a×3a=6a2,S△AEC===,S△AFB===a2,
S△CBG===a2,
∴S△ABC=S长方形EFGC﹣S△AEC﹣S△AFB﹣S△BGC=6a2﹣﹣a2﹣a2=,
在Rt△AEC中,
AC===,
∵S△ABC===,
解得BD=a,
在Rt△AFB中,
AB===,
在Rt△ABD中,
sin∠BAC===.
故选:C.
5.解:如图,过点C作CE⊥BA交BA的延长线于E.
∵∠BAC=120°,
∴∠CAE=180°﹣120°=60°,
∴AE=AC cos60°=4,EC=AC sin60°=4,
∵AB=4,
∴BE=AB+AE=8,
∴BC===4,
故选:B.
6.解:如图,过点P作PH⊥x轴于H.
∵P(2,4),
∴OH=2,PH=4,
∴OP===2,
∴sinα===,
故选:D.
7.解:如图,作CE⊥AB于E,
设小正方形边长为1,则易证△BEC是等腰直角三角形,
∴CE=BE=,AB==3,
∴AE=AB﹣BE==3﹣=,
在Rt△AEC中,tan∠EAC===.
∴tan∠BAC的值是,
故选:C.
8.解:作CQ∥AB,连接PC,如右图所示,
设每个小正方形的边长为1,
则CQ==2,PQ==2,PC==4,
∴CQ2+PC2=(2)2+(4)2=8+32=40=(2)2=PQ2,
∴△PCQ是直角三角形,∠PCQ=90°,
∴cos∠PQC===,
∵AB∥CQ,
∴∠QMB=∠PQC,
∴cos∠QMB的值是,
故选:A.
9.解:如图,分别过点A、D作AF⊥BC、DE⊥BC,交BC于点F、E,过点D作DM⊥AF,于点M,
在Rt△ABC中,
∵AB=5,∠ABC=45°,
∴AC=AB=5,BC=10,
∴AF=BF=5,
在Rt△BCD中,
∵tan∠DBC=,
∴BD=6,
在Rt△BDE中,
∵tan∠DBE=,
∴DE=,BE=,
∵∠DEF=∠DMF=∠EFM=90°,
∴四边形DEFM是矩形,
∴DM=EF=BF﹣BE=,MF=DE=,
∴AM=AF﹣MF=,
在Rt△ADM中,由勾股定理,得:AD==,
故答案为:.
10.解:如图,设直线x=﹣5交x轴于K,连接DK,由题意KD=CF=5,
∴点D的运动轨迹是以K为圆心,5为半径的圆,
∴当直线AD与⊙K相切时,△ABE的面积最小,
∵AD是切线,点D是切点,
∴AD⊥KD,
∵AK=13,DK=5,
∴AD=12,
∵tan∠EAO==,
∴=,
∴OE=,
∴AE==,
作EH⊥AB于H.
∵S△ABE= AB EH=S△AOB﹣S△AOE,
∴EH=,
∴AH==,
∴tan∠BAD===.
11.解:如图,在AE上取一点M,使得AM=MC.设EC=m.
∵cos∠BAC=,
∴∠BAC=45°,
∵AB=AC,AE平分∠BAC,
∴AE⊥BC,∠EAC=∠BAC=22.5°,
∵MA=MC,
∴∠MAC=∠MCA=22.5°,
∴∠CME=∠MAC+∠MCA=45°,
∴EC=EM=m,AM=CM=m,AE=m+m,
∵∠ADC=∠AEC=90°,
∴A,D,E,C四点共圆,
∴∠ECF=∠DAE=22.5°,
∵∠DAE=∠EAC,
∴=,
∴DE=ED,
∴===tan22.5°==﹣1.
故答案为:﹣1
12.解:如图:过点A作AE⊥BC,交BC于点E,
设DE=x,则CE=5﹣x,
在Rt△ABE中,AE2=AB2﹣BE2,
则AE2=62﹣(4﹣x)2①,
在Rt△ACE中,AE2=AC2﹣CE2,
则AE2=52﹣(5﹣x)2②,
由①②得,62﹣(4﹣x)2=52﹣(5﹣x)2,
解得:x=,则DE=,
在Rt△ADE中,AD2=AE2+DE2③,
将x=代入①式,得AE=,
则AD2=()2+()2,
解得AD=,
∴cos∠ADC==.
13.解:设BD=a,则由题意可得:BC=3a,AB=AD=a,
在△ABD中,由余弦定理得:cosA===,
∴sinA==,
在△ABC中,由正弦定理得,=,
即=,
解得:sinC=,
故答案为:.
14.解:过点F作FG⊥AB于点G,
∵∠ACB=90°,CD⊥AB,
∴∠CDA=90°,
∴∠CAF+∠CFA=90°,∠FAD+∠AED=90°,
∵AF平分∠CAB,
∴∠CAF=∠FAD,
∴∠CFA=∠AED=∠CEF,
∴CE=CF,
∵AF平分∠CAB,∠ACF=∠AGF=90°,
∴FC=FG,
∵∠B=∠B,∠FGB=∠ACB=90°,
∴△BFG∽△BAC,
∴=,
∵AC=6,∠ACB=90°,
∴tanB==
∴BC=8,AB===10,
∴=,
∵FC=FG,
解得:FC=3,
即CE的长为3.
故答案为:3.
15.解:如图,过点A作AE⊥BC交BC的延长线于E.
在Rt△ABE中,∠E=90°,AE=3,BE=4,
∴AB===5,
∴cosB==,sinB==,
∴cosB+sinB=+=,
故答案为:.
16.解:∵∠C=90°,∠A=∠CBD,cos∠CBD=,
∴cos∠A==,
∵AC=8cm,
∴AB=10cm.
故答案为:10.
17.解:如图所示:连接AE、BE.
∵AC=ED=1,AC∥ED,
∴四边形AEDC是平行四边形.
∴AE∥CD.
∴∠EAB=∠DPB.
∵BE=AE==,
AB===2.
∴AB2=AE2+BE2.
∴△AEB是等腰直角三角形.
∴∠EAB=∠DPB=45°.
∴sin∠BPD=sin45°=.
故答案为:.
18.解:(1)过点A作BD的垂线交BD的延长线于点E,
在Rt△ABE中,
∵∠ABC=30°,
∴AB=2AE,
BE==AE,
在Rt△ADE中,
∵∠ADC=45°,
∴DE=AE,
∴BD=BE﹣DE=AE﹣AE=(﹣1)AE,
∴==+1;
(2)如图,在AB上取一点E,使得DB=DE,连接EC.
∵DB=DE,
∴∠DBE=∠DEB=30°,
∴∠EDC=∠B+∠DEB=60°,
∵DB=DC=DE,
∴△DEC是等边三角形,
∴∠ECD=∠CED=60°,
∴∠CEB=∠CEA=90°,
∵∠ADC=45°,
∴∠EDA=∠EDC﹣∠ADC=15°,
∵∠DEB=∠EDA+∠AED,
∴∠EDA=∠EAD=15°,
∴ED=EA=EC,
∵∠CEA=90°,
∴∠ECA=45°,
∴∠ACB=∠ACE+∠ECB=45°+60°=105°.
19.证明:(1)∵点D、E分别是AB、BC的中点,
∴DE是△ABC的中位线,
∴DE∥AC.
∴∠DGB=∠AFB.
∵BF⊥AC,
∴∠AFB=∠BFC=90°.
∴∠DGB=90°,
∴DE⊥BF.
(2)∵∠BFC=90°,点E是BC的中点,
∴EF=BE=EC,
∴∠EFC=∠C.
∵AB=AC,
∴∠ABC=∠C.
∴∠CEF=180°﹣2∠C=∠BAC.
∵DE∥AC,点D是AB的中点,
∴△BDG∽△BAF,
∴=.
∵点E是BC的中点,
∴S△BFC=2S△CEF,
∵S△CEF=,
∴.
∴S△AFB=S△ABF+S△BCF=S△ABF+2S△CEF=S△CEF.
∴==S△CEF:S△CEF=,
在Rt△ABF中,cos∠CEF=cos∠BAF===.
20.解:(1)∵∠C=90°,AB=5,AC=3,
∴BC=
==
4.
∵D是BC的中点,
∴CD=BC=2.
∴AD=
=
=.
(2)过点D作DE⊥AB,垂足为E.
∵D为BC的中点,
∴S△ACD=S△ADB=AC×CD=3.
∵S△ABD=AB×DE=3,
∴DE=.
∴sin∠DAB=
=
=.
21.解:(1)∵∠CBD=∠A+∠ACB,∠A=45°,∠CBD=75°,
∴∠ACB=75°﹣45°=30°.
(2)如图,过点B作BH⊥AC于H.
∵∠BHA=90°,AB=60m,∠A=45°,
∴BH=AB sin45°=60(m),
∵∠BCH=30°,
∴BC=2BH=120(m).
22.解:(1)如图,作BH⊥CF于点H,
在Rt△ABC中,∠ACB=90°,∠A=60°,
∴∠ABC=30°,
∵AB∥CF,
∴∠BCH=∠ABC=30°,
∵AB=20,
∴,
在Rt△BCH中,∵∠BCH=30°,
∴,CH=BC×cos30°=15,
在Rt△DEF中,∵∠E=45°,
∴∠EDF=∠E=45°,
在Rt△BDH中,,
∴.
23.解:(1)如图,连接BD,设BC垂直平分线交BC于点F,
∴BD=CD,
C△ABD=AB+AD+BD
=AB+AD+DC
=AB+AC,
∵AB=CE,
∴C△ABD=AC+CE=AE=1,
故△ABD的周长为1.
(2)设AD=x,
∴BD=3x,
又∵BD=CD,
∴AC=AD+CD=4x,
在Rt△ABD中,AB===2.
∴tan∠ABC===.
24.解:(1)∵AC⊥BD,cos∠ABC==,BC=8,
∴AB=10,
在Rt△ACB中,由勾股定理得,
AC===6,
即AC的长为6;
(2)如图,
连接CF,过F点作BD的垂线,垂足E,
∵BF为AD边上的中线,
即F为AD的中点,
∴CF=AD=FD,
在Rt△ACD中,由勾股定理得,
AD===2,
∵三角形CFD为等腰三角形,FE⊥CD,
∴CE=CD=2,
在Rt△EFC中,EF===3,
∴tan∠FBD===.
解法二:∵BF为AD边上的中线,
∴F是AD中点,
∵FE⊥BD,AC⊥BD,
∴FE∥AC,
∴FE是△ACD的中位线,
∴FE=AC=3,CE=CD=2,
∴在Rt△BFE中,tan∠FBD===
