2021-2022学年九年级数学鲁教版(五四制)上册2.6 利用三角函数测高能力提升训练(word版、含答案)
文档属性
| 名称 | 2021-2022学年九年级数学鲁教版(五四制)上册2.6 利用三角函数测高能力提升训练(word版、含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 342.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-05 08:53:40 | ||
图片预览




文档简介
2021-2022学年鲁教版九年级数学上册《2.6利用三角函数测高》能力提升训练(附答案)
一、选择题
1.如图,一艘海轮位于灯塔P的南偏东37°方向,距离灯塔40海里的A处,它沿正北方向航行一段时间后,到达位于灯塔的正东方向上的B处,这时,B处与灯塔P的距离PB的长可以表示为( )
A.40海里
B.40sin37°海里
C.40cos37°海里
D.40tan37°海里
2.如图,一艘轮船以40海里/时的速度在海面上航行,当它行驶到A处时,发现它的北偏东30°方向有一灯塔B.轮船继续向北航行2小时后到达C处,发现灯塔B在它的北偏东60°方向.若轮船继续向北航行,那么当再过多长时间时轮船离灯塔最近?( )
A.1小时
B.小时
C.2小时
D.小时
3.我国北斗导航装备的不断更新,极大方便人们的出行.某中学组织学生利用导航到C地进行社会实践活动,到达A地时,发现C地恰好在A地正北方向,导航显示路线应沿北偏东60°方向走到B地,再沿北偏西37°方向走才能到达C地.如图所示,已知A,B两地相距6千米,则A,C两地的距离为( )(参考数据sin53°≈0.80,cos53°≈0.60,tan53°≈1.32)
A.12千米
B.(3+4)千米
C.(3+5)千米
D.(12﹣4)千米
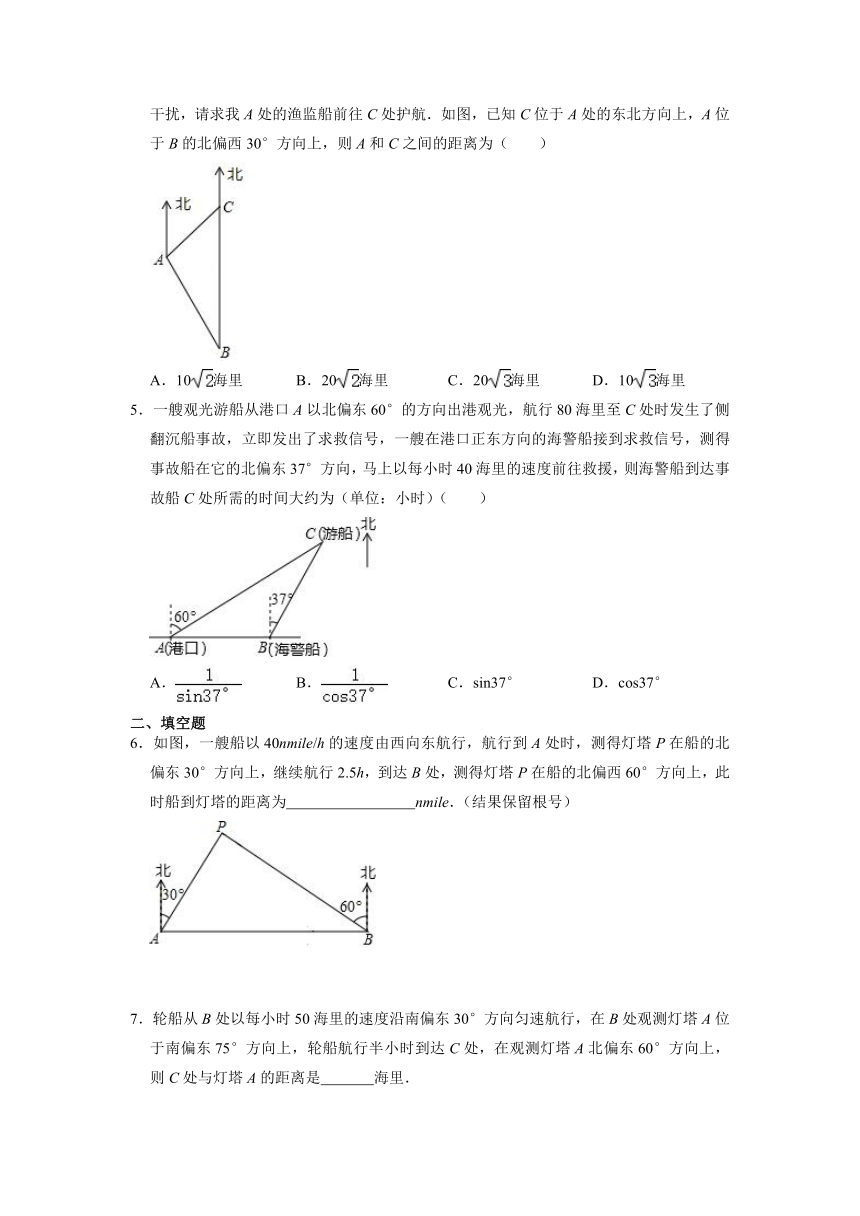
4.南沙群岛是我国固有领土,现在我南海渔民要在南沙某海岛附近进行捕鱼作业,当渔船航行至B处时,测得该岛位于正北方向10(1+)海里的C处,为了防止某国海巡警干扰,请求我A处的渔监船前往C处护航.如图,已知C位于A处的东北方向上,A位于B的北偏西30°方向上,则A和C之间的距离为( )
A.10海里
B.20海里
C.20海里
D.10海里
5.一艘观光游船从港口A以北偏东60°的方向出港观光,航行80海里至C处时发生了侧翻沉船事故,立即发出了求救信号,一艘在港口正东方向的海警船接到求救信号,测得事故船在它的北偏东37°方向,马上以每小时40海里的速度前往救援,则海警船到达事故船C处所需的时间大约为(单位:小时)( )
A.
B.
C.sin37°
D.cos37°
二、填空题
6.如图,一艘船以40nmile/h的速度由西向东航行,航行到A处时,测得灯塔P在船的北偏东30°方向上,继续航行2.5h,到达B处,测得灯塔P在船的北偏西60°方向上,此时船到灯塔的距离为
nmile.(结果保留根号)
7.轮船从B处以每小时50海里的速度沿南偏东30°方向匀速航行,在B处观测灯塔A位于南偏东75°方向上,轮船航行半小时到达C处,在观测灯塔A北偏东60°方向上,则C处与灯塔A的距离是
海里.
8.如图,我国的一艘海监船在钓鱼岛A附近沿正东方向航行,船在B点时测得钓鱼岛A在船的北偏东60°方向,船以50海里/时的速度继续航行2小时后到达C点,此时钓鱼岛A在船的北偏东30°方向.请问船继续航行
海里与钓鱼岛A的距离最近?
三、解答题
9.如图,一艘观光游船从港口A以北偏东60°的方向出港观光,航行80海里至C处时发生了侧翻沉船事故,立即发出了求救信号,一艘在港口正东方向的海警船接到求救信号,测得事故船在它的北偏东39°方向,马上以40海里每小时的速度前往救援,求海警船到大事故船C处所需的大约时间.(结果精确到0.01小时,sin39°≈0.629,cos39°≈0.777,tan39°≈0.810)
10.游艇在湖面上以12千米/小时的速度向正东方向航行,在O处看到灯塔A在游艇北偏东60°方向上,航行1小时到达B处,此时看到灯塔A在游艇北偏西30°方向上,求此时游艇与灯塔的距离AB.
11.一架外国侦察机沿ED方向侵入我国领空进行非法侦察,我空军的战斗机沿AC方向与外国侦察机平行飞行,进行跟踪监视,我机在A处与外国侦察机B处的距离为50米,∠CAB为30°,这时外国侦察机突然转向,以偏左45°的方向飞行,我机继续沿AC方向以400米/秒的速度飞行,外国侦察机在C点故意撞击我战斗机,使我战斗机受损.问外国侦察机由B到C的速度是多少?(结果保留整数,参考数据=1.414,=1.732)
12.如图,海中有一个小岛A,今有货轮由西向东航行,开始在A岛南偏西55°的B处,往东航行一段距离后到达该岛的南偏西25°的C处,货轮从C处继续向东航行14.1海里,此时货轮与A的距离最近,求货轮在B处时与小岛A的距离.(精确到0.1海里)(参考数据:sin25°≈0.42,cos25°=0.91,tan25°≈0.47,sin55°≈0.82,cos55°=0.57,tan55°≈1.43)
13.如图,一位旅行者骑自行车沿湖边正东方向笔直的公路BC行驶,在B地测得湖中小岛上某建筑物A在北偏东45°方向,行驶12min后到达C地,测得建筑物A在北偏西60°方向如果此旅行者的速度为10km/h,求建筑物A到公路BC的距离.(结果保留根号)
14.如图,一艘渔船以30海里/h的速度由西向东追赶鱼群.在A处测得小岛C在船的北偏东60°方向;40min后渔船行至B处,此时测得小岛C在船的北偏东30°方向.已知以小岛C为中心,周围10海里内有暗礁,问这艘渔船继续向东追赶鱼群是否有触礁的危险?
15.某时刻海上点P处有一客轮.测得灯塔A位于客轮P的北偏东30°方向,且相距20海里,客轮以每小时60海里的速度沿北偏西60°方向航行小时到达B处.那么tan∠ABP的值为多少?
16.如图,禁止捕鱼期间,某海上稽查队在某海域巡逻,上午某一时刻在A处接到指挥部通知,在他们东北方向距离12海里的B处有一艘捕鱼船,正在沿南偏东75°方向航行,稽查队员立即乘坐巡逻船以每小时14海里的速度沿北偏东某一方向出发行驶了2小时,在C处成功拦截捕鱼船,求捕鱼船的速度.
17.如图,灯塔A在港口P的南偏东45°方向,距离港口20海里处,一艘客轮从港口P出发,沿北偏东30°方向,以20海里/小时的速度驶离港口,客轮出发后几小时后在灯塔的正北方向,并求出此时客轮距灯塔的距离.
(参考数据:≈1.41,≈1.73).
18.如图,BC是某公园人工湖中的两个人造观光小岛,为了测量两个小岛BC之间的距离,工作人员在距离小岛C
100米的地方选择了一个固定观测点A,并测得小岛C在观测点A北偏东30°的方向上,与此同时,工作人员还测得小岛B在观测点A北偏东75°的方向上,请你利用工作人员测得的相关数据,计算观光小岛BC之间的距离.(结果精确到0.1米,参考数据:≈1.732,sin75°≈0.9659,cos75°≈0.2588,tan75°≈3.7321)
19.一渔船在海岛A北偏东30°方向的M处遇险,渔船将险情报告给位于A处的救援船后,沿南偏东75°方向向海岛C靠近,同时,从A处出发的救援船沿北偏东60°方向以每小时40海里的速度匀速航行,30分钟后,救援船在海岛C处恰好追上渔船,那么渔船遇险M处与海岛C的距离是多少海里?(≈1.4,≈1.7,≈2.4)
参考答案
1.解:∵一艘海轮位于灯塔P的南偏东37°方向,
∴∠BAP=37°,
∵AP=40海里,
∴BP=AP sin37°=40sin37°海里;
故选:B.
2.解:作BD⊥AC于D,如下图所示:
易知:∠DAB=30°,∠DCB=60°,
则∠CBD=∠CBA=30°.
∴AC=BC,
∵轮船以40海里/时的速度在海面上航行,
∴AC=BC=2×40=80海里,
∴CD=BC=40海里.
故该船需要继续航行的时间为40÷40=1小时.
故选:A.
3.解:如图,作BD⊥AC于点D,
根据题意可知:
在Rt△ADB中,∠A=60°,AB=6千米,
∴AD=3千米,BD=3千米,
在Rt△CDB中,∠CBD=53°,
∴CD=BD tan53°≈3×1.32≈3×≈4(千米),
∴AC=AD+CD=3+4(千米).
则A,C两地的距离为(3+4)千米.
故选:B.
4.解:过点A作AD⊥BC于点D,如图所示.
∵C位于A处的东北方向上,A位于B的北偏西30°方向上,
∴CD=AD tan45°=AD,AC==AD,BD==AD.
设AD=x,则CD=x,AC=x,BD=x.
∵BC=BD+CD=(+1)x=10(1+),
∴x=10,
∴AC=10.
故选:A.
5.解:如图,过点C作CD⊥AB交AB延长线于D.
在Rt△ACD中,∵∠ADC=90°,∠CAD=30°,AC=80海里,
∴CD=AC=40海里.
在Rt△CBD中,∵∠CDB=90°,∠BCD=37°,
∴BC==海里,
∴海警船到大事故船C处所需的时间大约为:÷40=(小时).
故选:B.
6.解:根据题意,得:∠PAB=60°,∠PBA=30°,AB=2.5×40=100(nmile),
∴∠P=180°﹣∠PAB﹣∠PBA=180°﹣60°﹣30°=90°.
在Rt△PAB中,PB=AB sin∠PAB=100×=50(nmile).
故答案为:50.
7.解:根据题意,得∠1=∠2=30°,
∵∠ACD=60°,
∴∠ACB=30°+60°=90°,
∴∠CBA=75°﹣30°=45°,
∴△ABC为等腰直角三角形,
∵BC=50×0.5=25,
∴AC=BC=25(海里).
故答案为:25.
8.解:过点A作AD⊥BC于D,则∠ABC=30°,∠ACD=60°,
∴∠BAC=∠ACD﹣∠ABC=30°,
∴CA=CB.
∵CB=50×2=100(海里),
∴CA=100(海里),
在直角△ADC中,∠ACD=60°,
∴CD=AC=×100=50(海里).
则船继续航行50海里与钓鱼岛A的距离最近;
故答案为:50.
9.解:如图,过点C作CD⊥AB交AB延长线于D.
在Rt△ACD中,∵∠ADC=90°,∠CAD=30°,AC=80海里,
∴CD=AC=40海里.
在Rt△CBD中,∵∠CDB=90°,∠BCD=39°,
∴BC==海里,
∴海警船到大事故船C处所需的时间大约为:÷40=≈1.29(小时).
答:海警船到大事故船C处所需的大约时间为1.29小时.
10.解:方法一:
过点A作AC⊥OB交OB于C,则AC为所求,设AC=x,
由题意得:OB=12千米,∠AOC=30°,∠ABC=60°,
在Rt△ACO和Rt△ACB中:
tan30°=,tan60°=,
则OC=x,BC=x,
而OC+CB=x+x=12,
解得:x=3.
故AB===6(千米),
答:此时游艇与灯塔的距离AB为6千米.
方法二:
由题意得:OB=12千米,∠AOB=30°,∠ABO=60°,
则∠OAB=90°,
故AB=OB=6(千米),
答:此时游艇与灯塔的距离AB为6千米.
11.解:过点B作BF⊥AC于点F,
∵∠CBD=45°,
∴∠CBF=∠C=45°,
∵∠A=30°,AB=50,
∴BF=25m,AF=25m,
∴FC=25m,则BC=25m,
∴AC=25+25≈68(m),
68÷400≈0.17(秒),
故25÷0.17≈208(m/s),
答:外国侦察机由B到C的速度是208m/s.
12.解:如图,作AD⊥BC于点D,
在Rt△ACD中,∵∠ADC=90°,∠CAD=25°,CD=14.1海里,
∴AD=≈=30(海里).
在Rt△ABD中,∵∠ADB=90°,∠BAD=55°,
∴AB=≈≈52.6(海里).
答:货轮在B处时与小岛A的距离约为52.6海里.
13.解:过点A作AD⊥BC,垂足为点D.如图,
依题意得∠ABC=45°,∠ACB=30°,则∠BAD=45°.
∴AD=BD,
在Rt△ACD中,∵∠ACB=30°,
∴AC=2AD,CD=AD,
设AD=x
km,则BD=AD=x,AC=2x,CD=x,
又∵BC=12×=2
∴x+x=2,解得:x=﹣1.
所以建筑物A到公路BC的距离为(﹣1)km.
14.解:作CD⊥AB于D,
根据题意,AB=30×=20(海里),∠CAD=30°,∠CBD=60°,
在Rt△ACD中,AD==CD,
在Rt△BCD中,BD==CD,
∵AB=AD﹣BD,
∴CD﹣CD=20(海里),
解得:CD=10>10,
所以不可能.
15.解:如图.
∵灯塔A位于客轮P的北偏东30°方向,且相距20海里.
∴PA=20海里,
∵客轮以60海里/小时的速度沿北偏西60°方向航行小时到达B处,
∴∠APB=90°,BP=60×=40海里,
∴tan∠ABP===.
故tan∠ABP的值为.
16.解:设捕鱼船的速度为x海里/小时;如图所示,
由题意得:∠ABC=45°+75°=120°,AB=12,BC=2x,AC=14×2=28,
过点A作AD⊥CB的延长线于点D,
在Rt△ABD中,AB=12,∠ABD=45°+(90°﹣75°)=60°,
∴BD=AB cos60°=AB=6,AD=AB sin60°=6,
∴CD=2x+6.
在Rt△ACD中,由勾股定理得:282=(6)2+(2x+6)2,
解得:x=10,(负值舍去),
答:捕鱼船的速度为10海里/小时.
17.解:如图所示,∵Rt△ACP中,∠APC=45°,AP=20,
∴PC=cos45°×AP=×20=20,AC=20,
又∵Rt△BCP中,∠BPC=60°,
∴∠B=30°,
∴BP=2PC=40,
∴客轮行驶到灯塔的正北方向的时间为:40÷20=2小时,
此时,Rt△BCP中,BC=tan60°×PC=20,
∴AB=BC+AC=20+20≈54.6,
此时客轮距灯塔的距离为54.6海里.
18.解:如图所示,延长BC交AE于D,则∠ADC=90°,
∵∠CAD=30°,AC=100,
∴CD=AC=50,AD=cos30°×AC=50,
∵Rt△ABD中,tan∠BAD=,
∴3.7321≈,
解得BC≈273.2,
答:观光小岛BC之间的距离为273.2米.
19.解:作MN⊥AC于点N,如右图所示,
由题意可得,
∠MAC=60°﹣30°=30°,∠AMC=75°+30°=105°,
∴∠MCA=180°﹣∠MAC﹣∠AMC=180°﹣30°﹣105°=45°,
∵MN⊥AC,AC=40,
∴∠MVA=∠MNC=90°,
∴MN=NC,
设NC=a,
∴MN=a,MN=(20) tan30°,
解得,a=,
∴MC===≈20×1.7﹣20=14(海里),
即渔船遇险M处与海岛C的距离是14海里.
一、选择题
1.如图,一艘海轮位于灯塔P的南偏东37°方向,距离灯塔40海里的A处,它沿正北方向航行一段时间后,到达位于灯塔的正东方向上的B处,这时,B处与灯塔P的距离PB的长可以表示为( )
A.40海里
B.40sin37°海里
C.40cos37°海里
D.40tan37°海里
2.如图,一艘轮船以40海里/时的速度在海面上航行,当它行驶到A处时,发现它的北偏东30°方向有一灯塔B.轮船继续向北航行2小时后到达C处,发现灯塔B在它的北偏东60°方向.若轮船继续向北航行,那么当再过多长时间时轮船离灯塔最近?( )
A.1小时
B.小时
C.2小时
D.小时
3.我国北斗导航装备的不断更新,极大方便人们的出行.某中学组织学生利用导航到C地进行社会实践活动,到达A地时,发现C地恰好在A地正北方向,导航显示路线应沿北偏东60°方向走到B地,再沿北偏西37°方向走才能到达C地.如图所示,已知A,B两地相距6千米,则A,C两地的距离为( )(参考数据sin53°≈0.80,cos53°≈0.60,tan53°≈1.32)
A.12千米
B.(3+4)千米
C.(3+5)千米
D.(12﹣4)千米
4.南沙群岛是我国固有领土,现在我南海渔民要在南沙某海岛附近进行捕鱼作业,当渔船航行至B处时,测得该岛位于正北方向10(1+)海里的C处,为了防止某国海巡警干扰,请求我A处的渔监船前往C处护航.如图,已知C位于A处的东北方向上,A位于B的北偏西30°方向上,则A和C之间的距离为( )
A.10海里
B.20海里
C.20海里
D.10海里
5.一艘观光游船从港口A以北偏东60°的方向出港观光,航行80海里至C处时发生了侧翻沉船事故,立即发出了求救信号,一艘在港口正东方向的海警船接到求救信号,测得事故船在它的北偏东37°方向,马上以每小时40海里的速度前往救援,则海警船到达事故船C处所需的时间大约为(单位:小时)( )
A.
B.
C.sin37°
D.cos37°
二、填空题
6.如图,一艘船以40nmile/h的速度由西向东航行,航行到A处时,测得灯塔P在船的北偏东30°方向上,继续航行2.5h,到达B处,测得灯塔P在船的北偏西60°方向上,此时船到灯塔的距离为
nmile.(结果保留根号)
7.轮船从B处以每小时50海里的速度沿南偏东30°方向匀速航行,在B处观测灯塔A位于南偏东75°方向上,轮船航行半小时到达C处,在观测灯塔A北偏东60°方向上,则C处与灯塔A的距离是
海里.
8.如图,我国的一艘海监船在钓鱼岛A附近沿正东方向航行,船在B点时测得钓鱼岛A在船的北偏东60°方向,船以50海里/时的速度继续航行2小时后到达C点,此时钓鱼岛A在船的北偏东30°方向.请问船继续航行
海里与钓鱼岛A的距离最近?
三、解答题
9.如图,一艘观光游船从港口A以北偏东60°的方向出港观光,航行80海里至C处时发生了侧翻沉船事故,立即发出了求救信号,一艘在港口正东方向的海警船接到求救信号,测得事故船在它的北偏东39°方向,马上以40海里每小时的速度前往救援,求海警船到大事故船C处所需的大约时间.(结果精确到0.01小时,sin39°≈0.629,cos39°≈0.777,tan39°≈0.810)
10.游艇在湖面上以12千米/小时的速度向正东方向航行,在O处看到灯塔A在游艇北偏东60°方向上,航行1小时到达B处,此时看到灯塔A在游艇北偏西30°方向上,求此时游艇与灯塔的距离AB.
11.一架外国侦察机沿ED方向侵入我国领空进行非法侦察,我空军的战斗机沿AC方向与外国侦察机平行飞行,进行跟踪监视,我机在A处与外国侦察机B处的距离为50米,∠CAB为30°,这时外国侦察机突然转向,以偏左45°的方向飞行,我机继续沿AC方向以400米/秒的速度飞行,外国侦察机在C点故意撞击我战斗机,使我战斗机受损.问外国侦察机由B到C的速度是多少?(结果保留整数,参考数据=1.414,=1.732)
12.如图,海中有一个小岛A,今有货轮由西向东航行,开始在A岛南偏西55°的B处,往东航行一段距离后到达该岛的南偏西25°的C处,货轮从C处继续向东航行14.1海里,此时货轮与A的距离最近,求货轮在B处时与小岛A的距离.(精确到0.1海里)(参考数据:sin25°≈0.42,cos25°=0.91,tan25°≈0.47,sin55°≈0.82,cos55°=0.57,tan55°≈1.43)
13.如图,一位旅行者骑自行车沿湖边正东方向笔直的公路BC行驶,在B地测得湖中小岛上某建筑物A在北偏东45°方向,行驶12min后到达C地,测得建筑物A在北偏西60°方向如果此旅行者的速度为10km/h,求建筑物A到公路BC的距离.(结果保留根号)
14.如图,一艘渔船以30海里/h的速度由西向东追赶鱼群.在A处测得小岛C在船的北偏东60°方向;40min后渔船行至B处,此时测得小岛C在船的北偏东30°方向.已知以小岛C为中心,周围10海里内有暗礁,问这艘渔船继续向东追赶鱼群是否有触礁的危险?
15.某时刻海上点P处有一客轮.测得灯塔A位于客轮P的北偏东30°方向,且相距20海里,客轮以每小时60海里的速度沿北偏西60°方向航行小时到达B处.那么tan∠ABP的值为多少?
16.如图,禁止捕鱼期间,某海上稽查队在某海域巡逻,上午某一时刻在A处接到指挥部通知,在他们东北方向距离12海里的B处有一艘捕鱼船,正在沿南偏东75°方向航行,稽查队员立即乘坐巡逻船以每小时14海里的速度沿北偏东某一方向出发行驶了2小时,在C处成功拦截捕鱼船,求捕鱼船的速度.
17.如图,灯塔A在港口P的南偏东45°方向,距离港口20海里处,一艘客轮从港口P出发,沿北偏东30°方向,以20海里/小时的速度驶离港口,客轮出发后几小时后在灯塔的正北方向,并求出此时客轮距灯塔的距离.
(参考数据:≈1.41,≈1.73).
18.如图,BC是某公园人工湖中的两个人造观光小岛,为了测量两个小岛BC之间的距离,工作人员在距离小岛C
100米的地方选择了一个固定观测点A,并测得小岛C在观测点A北偏东30°的方向上,与此同时,工作人员还测得小岛B在观测点A北偏东75°的方向上,请你利用工作人员测得的相关数据,计算观光小岛BC之间的距离.(结果精确到0.1米,参考数据:≈1.732,sin75°≈0.9659,cos75°≈0.2588,tan75°≈3.7321)
19.一渔船在海岛A北偏东30°方向的M处遇险,渔船将险情报告给位于A处的救援船后,沿南偏东75°方向向海岛C靠近,同时,从A处出发的救援船沿北偏东60°方向以每小时40海里的速度匀速航行,30分钟后,救援船在海岛C处恰好追上渔船,那么渔船遇险M处与海岛C的距离是多少海里?(≈1.4,≈1.7,≈2.4)
参考答案
1.解:∵一艘海轮位于灯塔P的南偏东37°方向,
∴∠BAP=37°,
∵AP=40海里,
∴BP=AP sin37°=40sin37°海里;
故选:B.
2.解:作BD⊥AC于D,如下图所示:
易知:∠DAB=30°,∠DCB=60°,
则∠CBD=∠CBA=30°.
∴AC=BC,
∵轮船以40海里/时的速度在海面上航行,
∴AC=BC=2×40=80海里,
∴CD=BC=40海里.
故该船需要继续航行的时间为40÷40=1小时.
故选:A.
3.解:如图,作BD⊥AC于点D,
根据题意可知:
在Rt△ADB中,∠A=60°,AB=6千米,
∴AD=3千米,BD=3千米,
在Rt△CDB中,∠CBD=53°,
∴CD=BD tan53°≈3×1.32≈3×≈4(千米),
∴AC=AD+CD=3+4(千米).
则A,C两地的距离为(3+4)千米.
故选:B.
4.解:过点A作AD⊥BC于点D,如图所示.
∵C位于A处的东北方向上,A位于B的北偏西30°方向上,
∴CD=AD tan45°=AD,AC==AD,BD==AD.
设AD=x,则CD=x,AC=x,BD=x.
∵BC=BD+CD=(+1)x=10(1+),
∴x=10,
∴AC=10.
故选:A.
5.解:如图,过点C作CD⊥AB交AB延长线于D.
在Rt△ACD中,∵∠ADC=90°,∠CAD=30°,AC=80海里,
∴CD=AC=40海里.
在Rt△CBD中,∵∠CDB=90°,∠BCD=37°,
∴BC==海里,
∴海警船到大事故船C处所需的时间大约为:÷40=(小时).
故选:B.
6.解:根据题意,得:∠PAB=60°,∠PBA=30°,AB=2.5×40=100(nmile),
∴∠P=180°﹣∠PAB﹣∠PBA=180°﹣60°﹣30°=90°.
在Rt△PAB中,PB=AB sin∠PAB=100×=50(nmile).
故答案为:50.
7.解:根据题意,得∠1=∠2=30°,
∵∠ACD=60°,
∴∠ACB=30°+60°=90°,
∴∠CBA=75°﹣30°=45°,
∴△ABC为等腰直角三角形,
∵BC=50×0.5=25,
∴AC=BC=25(海里).
故答案为:25.
8.解:过点A作AD⊥BC于D,则∠ABC=30°,∠ACD=60°,
∴∠BAC=∠ACD﹣∠ABC=30°,
∴CA=CB.
∵CB=50×2=100(海里),
∴CA=100(海里),
在直角△ADC中,∠ACD=60°,
∴CD=AC=×100=50(海里).
则船继续航行50海里与钓鱼岛A的距离最近;
故答案为:50.
9.解:如图,过点C作CD⊥AB交AB延长线于D.
在Rt△ACD中,∵∠ADC=90°,∠CAD=30°,AC=80海里,
∴CD=AC=40海里.
在Rt△CBD中,∵∠CDB=90°,∠BCD=39°,
∴BC==海里,
∴海警船到大事故船C处所需的时间大约为:÷40=≈1.29(小时).
答:海警船到大事故船C处所需的大约时间为1.29小时.
10.解:方法一:
过点A作AC⊥OB交OB于C,则AC为所求,设AC=x,
由题意得:OB=12千米,∠AOC=30°,∠ABC=60°,
在Rt△ACO和Rt△ACB中:
tan30°=,tan60°=,
则OC=x,BC=x,
而OC+CB=x+x=12,
解得:x=3.
故AB===6(千米),
答:此时游艇与灯塔的距离AB为6千米.
方法二:
由题意得:OB=12千米,∠AOB=30°,∠ABO=60°,
则∠OAB=90°,
故AB=OB=6(千米),
答:此时游艇与灯塔的距离AB为6千米.
11.解:过点B作BF⊥AC于点F,
∵∠CBD=45°,
∴∠CBF=∠C=45°,
∵∠A=30°,AB=50,
∴BF=25m,AF=25m,
∴FC=25m,则BC=25m,
∴AC=25+25≈68(m),
68÷400≈0.17(秒),
故25÷0.17≈208(m/s),
答:外国侦察机由B到C的速度是208m/s.
12.解:如图,作AD⊥BC于点D,
在Rt△ACD中,∵∠ADC=90°,∠CAD=25°,CD=14.1海里,
∴AD=≈=30(海里).
在Rt△ABD中,∵∠ADB=90°,∠BAD=55°,
∴AB=≈≈52.6(海里).
答:货轮在B处时与小岛A的距离约为52.6海里.
13.解:过点A作AD⊥BC,垂足为点D.如图,
依题意得∠ABC=45°,∠ACB=30°,则∠BAD=45°.
∴AD=BD,
在Rt△ACD中,∵∠ACB=30°,
∴AC=2AD,CD=AD,
设AD=x
km,则BD=AD=x,AC=2x,CD=x,
又∵BC=12×=2
∴x+x=2,解得:x=﹣1.
所以建筑物A到公路BC的距离为(﹣1)km.
14.解:作CD⊥AB于D,
根据题意,AB=30×=20(海里),∠CAD=30°,∠CBD=60°,
在Rt△ACD中,AD==CD,
在Rt△BCD中,BD==CD,
∵AB=AD﹣BD,
∴CD﹣CD=20(海里),
解得:CD=10>10,
所以不可能.
15.解:如图.
∵灯塔A位于客轮P的北偏东30°方向,且相距20海里.
∴PA=20海里,
∵客轮以60海里/小时的速度沿北偏西60°方向航行小时到达B处,
∴∠APB=90°,BP=60×=40海里,
∴tan∠ABP===.
故tan∠ABP的值为.
16.解:设捕鱼船的速度为x海里/小时;如图所示,
由题意得:∠ABC=45°+75°=120°,AB=12,BC=2x,AC=14×2=28,
过点A作AD⊥CB的延长线于点D,
在Rt△ABD中,AB=12,∠ABD=45°+(90°﹣75°)=60°,
∴BD=AB cos60°=AB=6,AD=AB sin60°=6,
∴CD=2x+6.
在Rt△ACD中,由勾股定理得:282=(6)2+(2x+6)2,
解得:x=10,(负值舍去),
答:捕鱼船的速度为10海里/小时.
17.解:如图所示,∵Rt△ACP中,∠APC=45°,AP=20,
∴PC=cos45°×AP=×20=20,AC=20,
又∵Rt△BCP中,∠BPC=60°,
∴∠B=30°,
∴BP=2PC=40,
∴客轮行驶到灯塔的正北方向的时间为:40÷20=2小时,
此时,Rt△BCP中,BC=tan60°×PC=20,
∴AB=BC+AC=20+20≈54.6,
此时客轮距灯塔的距离为54.6海里.
18.解:如图所示,延长BC交AE于D,则∠ADC=90°,
∵∠CAD=30°,AC=100,
∴CD=AC=50,AD=cos30°×AC=50,
∵Rt△ABD中,tan∠BAD=,
∴3.7321≈,
解得BC≈273.2,
答:观光小岛BC之间的距离为273.2米.
19.解:作MN⊥AC于点N,如右图所示,
由题意可得,
∠MAC=60°﹣30°=30°,∠AMC=75°+30°=105°,
∴∠MCA=180°﹣∠MAC﹣∠AMC=180°﹣30°﹣105°=45°,
∵MN⊥AC,AC=40,
∴∠MVA=∠MNC=90°,
∴MN=NC,
设NC=a,
∴MN=a,MN=(20) tan30°,
解得,a=,
∴MC===≈20×1.7﹣20=14(海里),
即渔船遇险M处与海岛C的距离是14海里.
