2021-2022学年九年级数学鲁教版(五四制)上册第1章反比例函数单元能力提升训练(word版、含解析)
文档属性
| 名称 | 2021-2022学年九年级数学鲁教版(五四制)上册第1章反比例函数单元能力提升训练(word版、含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 535.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-05 08:59:14 | ||
图片预览


文档简介
2021-2022学年鲁教版九年级数学上册《第1章反比例函数》单元能力提升训练(附答案)
一、选择题
1.若函数y=(m2﹣3m+2)x|m|﹣3是反比例函数,则m的值是( )
A.1
B.﹣2
C.2或﹣2
D.2
2.下列关系式中,y是x的反比例函数的是( )
A.y=3x
B.y=5x+1
C.y=﹣x﹣1
D.y=x2﹣3
3.函数y=kx+b与y=(kb≠0)在同一坐标系中的图象可能是图中的( )
A.
B.
C.
D.
4.下列关于反比例函数y=﹣的结论中正确的是( )
A.图象过点(2,3)
B.图象在二、四象限内
C.在每个象限内,y随x的增大而减小
D.当x>﹣1时,y>6
5.已知关于x的方程x2﹣(m﹣1)x+1=0有两个相等的实数根,且反比例函数y=的图象在每个象限内y随x的增大而增大,那么m的值为( )
A.﹣1
B.3或﹣1
C.﹣2
D.3
6.已知点A(x1,y1),B(x2,y2),C(x3,y3)都在反比例函数y=(a是常数)的图象上,且y1<y2<0<y3,则x1,x2,x3的大小关系为( )
A.x2>x1>x3
B.x1>x2>x3
C.x3>x2>x1
D.x3>x1>x2
7.已知点A(x1,y1),B(x2,y2)都在反比例函数y=﹣的图象上,且x1<0<x2,则y1,y2的关系是( )
A.y2<0<y1
B.0<y2<y1
C.y1<y2<0
D.y1<0<y2
8.如图,菱形ABCD的顶点C,D分别在x轴,y轴上,BD∥x轴,反比例函数y=(x<0)的图象过菱形的对称中心E,若菱形的面积为8,则该反比例函数的解析式为( )
A.y=
B.y=﹣
C.y=
D.y=﹣
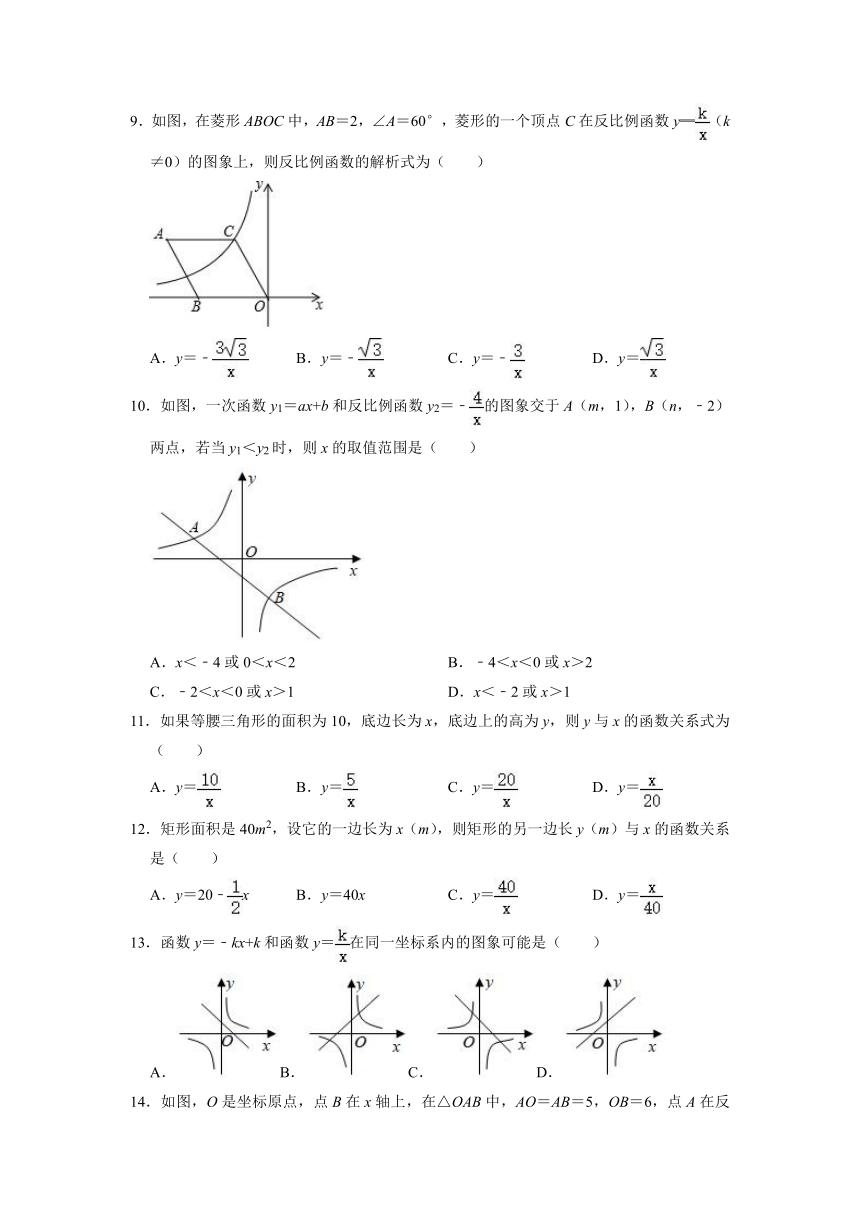
9.如图,在菱形ABOC中,AB=2,∠A=60°,菱形的一个顶点C在反比例函数y═(k≠0)的图象上,则反比例函数的解析式为( )
A.y=﹣
B.y=﹣
C.y=﹣
D.y=
10.如图,一次函数y1=ax+b和反比例函数y2=﹣的图象交于A(m,1),B(n,﹣2)两点,若当y1<y2时,则x的取值范围是( )
A.x<﹣4或0<x<2
B.﹣4<x<0或x>2
C.﹣2<x<0或x>1
D.x<﹣2或x>1
11.如果等腰三角形的面积为10,底边长为x,底边上的高为y,则y与x的函数关系式为( )
A.y=
B.y=
C.y=
D.y=
12.矩形面积是40m2,设它的一边长为x(m),则矩形的另一边长y(m)与x的函数关系是( )
A.y=20﹣x
B.y=40x
C.y=
D.y=
13.函数y=﹣kx+k和函数y=在同一坐标系内的图象可能是( )
A.B.C.D.
14.如图,O是坐标原点,点B在x轴上,在△OAB中,AO=AB=5,OB=6,点A在反比例函数y=(k≠0)图象上,则k的值( )
A.﹣12
B.﹣15
C.﹣20
D.﹣30
15.如图,在△OAB中,∠BOA=45°,点C为边AB上一点,且BC=2AC.如果函数y=(x>0)的图象经过点B和点C,那么用下列坐标表示的点,在直线BC上的是( )
A.(﹣2019,674)
B.(﹣2020,675)
C.(2021,﹣669)
D.(2022,﹣670)
二、填空题
16.已知函数y=(k2+k)x是反比例函数,则k的值为
.
17.若是反比例函数,则m满足的条件是
.
18.直线y=k1x+b与双曲线y=在同一平面直角坐标系中的图象如图所示,则关于x的不等式>k1x+b的解集为
.
19.已知一个函数的图象与反比例函数y=的图象关于y轴对称,则这个函数的表达式是
.
20.已知正比例函数y=k1x与反比例函数y=的一个交点是(2,3),则另一个交点是(
,
).
21.若一次函数y=ax+b的图象经过第一、三、四象限,则函数y=的图象位于第
象限.
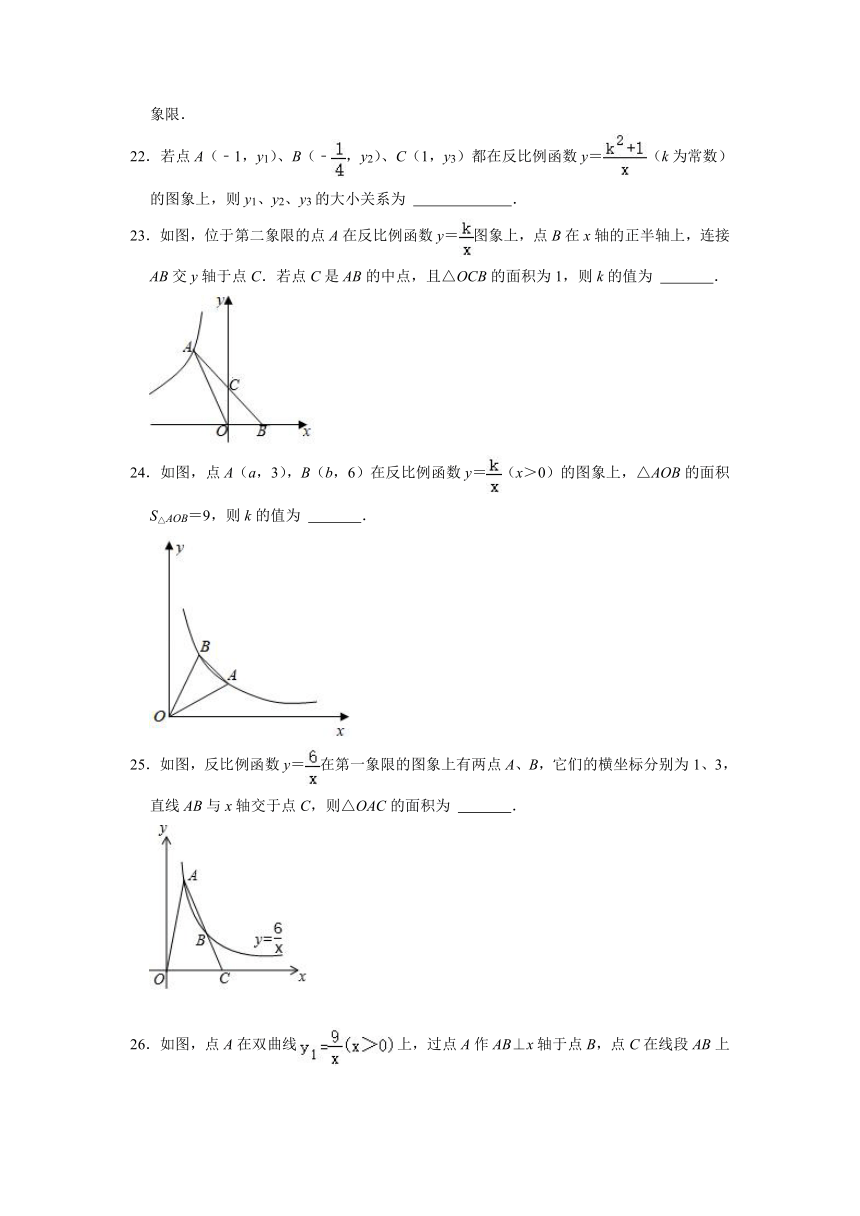
22.若点A(﹣1,y1)、B(﹣,y2)、C(1,y3)都在反比例函数y=(k为常数)的图象上,则y1、y2、y3的大小关系为
.
23.如图,位于第二象限的点A在反比例函数y=图象上,点B在x轴的正半轴上,连接AB交y轴于点C.若点C是AB的中点,且△OCB的面积为1,则k的值为
.
24.如图,点A(a,3),B(b,6)在反比例函数y=(x>0)的图象上,△AOB的面积S△AOB=9,则k的值为
.
25.如图,反比例函数y=在第一象限的图象上有两点A、B,它们的横坐标分别为1、3,直线AB与x轴交于点C,则△OAC的面积为
.
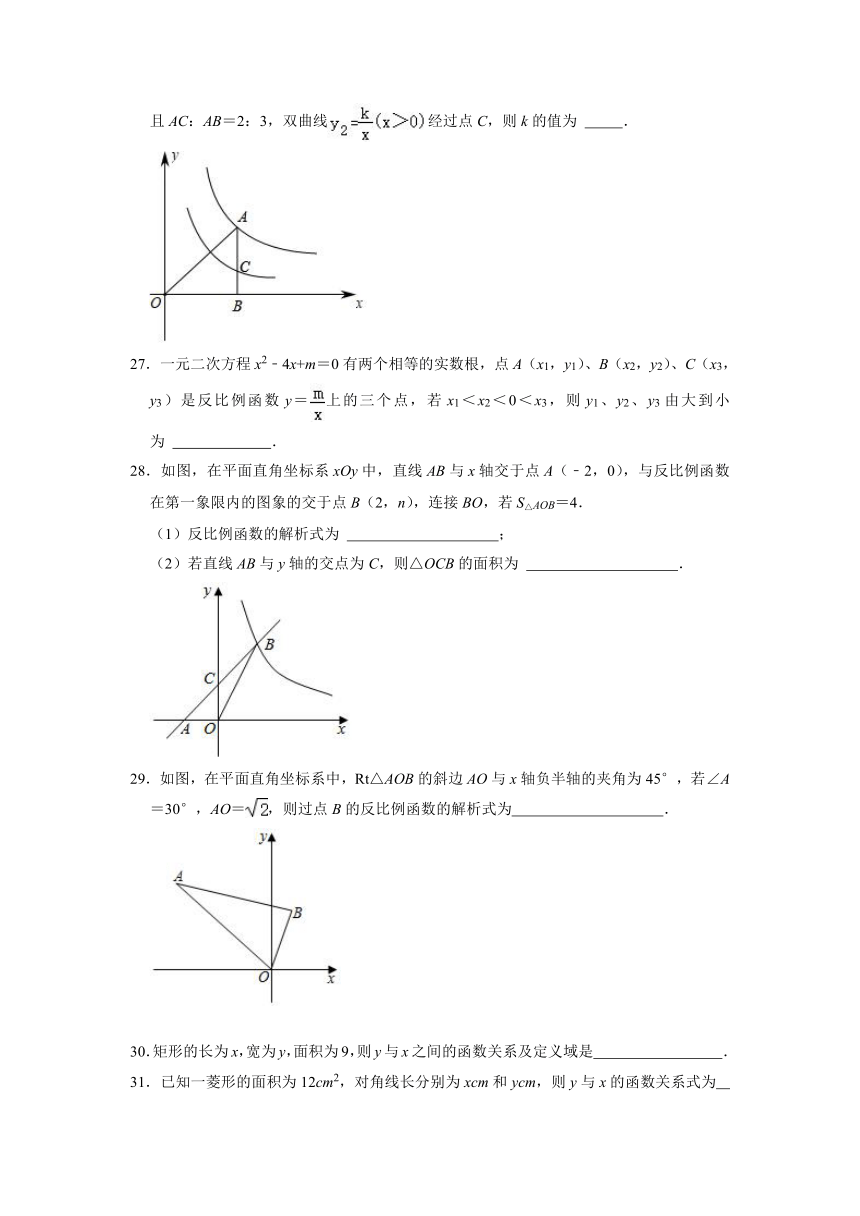
26.如图,点A在双曲线上,过点A作AB⊥x轴于点B,点C在线段AB上且AC:AB=2:3,双曲线经过点C,则k的值为
.
27.一元二次方程x2﹣4x+m=0有两个相等的实数根,点A(x1,y1)、B(x2,y2)、C(x3,y3)是反比例函数y=上的三个点,若x1<x2<0<x3,则y1、y2、y3由大到小为
.
28.如图,在平面直角坐标系xOy中,直线AB与x轴交于点A(﹣2,0),与反比例函数在第一象限内的图象的交于点B(2,n),连接BO,若S△AOB=4.
(1)反比例函数的解析式为
;
(2)若直线AB与y轴的交点为C,则△OCB的面积为
.
29.如图,在平面直角坐标系中,Rt△AOB的斜边AO与x轴负半轴的夹角为45°,若∠A=30°,AO=,则过点B的反比例函数的解析式为
.
30.矩形的长为x,宽为y,面积为9,则y与x之间的函数关系及定义域是
.
31.已知一菱形的面积为12cm2,对角线长分别为xcm和ycm,则y与x的函数关系式为
32.为了响应“绿水青山就是金山银山”的号召,建设生态文明,某工厂自2020年1月开始限产进行治污改造,其月利润y(万元)与月份x(月)之间的变化关系如图所示,治污完成前是反比例函数图象的一部分,治污完成后是一次函数图象的一部分,则4月份的利润为
万元,9月份的利润为
万元.
33.在平面直角坐标系中,一次函数y=2x与反比例函数y=(k≠0)的图象交于A(x1,y1),B(x2,y2)两点,则y1+y2的值是
.
34.一元二次方程x2﹣4x+m=0有两个相等的实数根,点A(x1,y1)、B(x2,y2)是反比例函数y=上的两个点,若x1<x2<0,则y1
y2(填“<”或“>”或“=”).
35.如图,点A、B在反比例函数y=(x>0)的图象上,延长AB交x轴于C点,若△AOC的面积是12,且点B是AC的中点,则k=
.
三、解答题
36.如图,已知A(﹣5,n),B(3,﹣5)是一次函数y=kx+b的图象和反比例函数y=的图象的两个交点.
(1)求反比例函数和一次函数的解析式;
(2)求△AOB的面积;
(3)结合图象,直接写出不等式kx+b﹣<0的解集.
37.如图,一次函数y=kx+b的图象与反比例函数y=的图象交于点A(1,3),B(3,n).
(1)求这两个函数的表达式;
(2)请结合图象直接写出不等式kx+b≥的解集;
(3)若点P为y轴上一点,△PAB的面积为4,求点P的坐标.
38.已知一次函数y=kx+b的图象与反比例函数y=的图象在第一象限交于点A,与x轴交于点B,与y轴交于点C(0,﹣8),若CB=AB,且S△OAB=8.
(1)求反比例函数与一次函数的解析式;
(2)直接写出kx+b﹣<0的解集;
(3)若点P为y轴上一点,求使∠APB=90°的点P的坐标.
39.如图,在平面直角坐标系中,直线y1=k1x+b与双曲线y2=相交于A(﹣2,3),B(m,﹣2)两点.
(1)求y1,y2对应的函数表达式;
(2)过点B作BP∥x轴交y轴于点P,求△ABP的面积;
(3)根据函数图象,直接写出关于x的不等式k1x+b<的解集.
40.如图,一次函数y=kx﹣2k(k≠0)的图象与反比例函数y=(m﹣1≠0)的图象交于点C,与x轴交于点A,过点C作CB⊥y轴,垂足为B,若S△ABC=3.
(1)求点A的坐标及m的值;
(2)若AB=2,求一次函数的表达式.
参考答案
1.解:∵函数y=(m2﹣3m+2)x|m|﹣3是反比例函数,
∴|m|﹣3=﹣1,且m2﹣3m+2≠0,
∴m=±2,
当m=2时,m2﹣3m+2=0,不合题意舍去,
当m=﹣2时,m2﹣3m+2=12≠0,
∴m=﹣2,
故选:B.
2.解:A.是正比例函数,不是反比例函数,故本选项不符合题意;
B.是一次函数,不是反比例函数,故本选项不符合题意;
C.是反比例函数,故本选项符合题意;
D.是二次函数,不是反比例函数,故本选项不符合题意;
故选:C.
3.解:A、函数y=kx+b的图象经过第一、二、四象限,则k<0,b>0,则kb<0,所以函数y=(kb≠0)的图象经过第二、四象限,故A选项不符合题意;
B、函数y=kx+b的图象经过第二、三、四象限,则k<0,b<0,则kb>0,所以函数y=(kb≠0)的图象经过第一、三象限,故B选项不符合题意;
C、函数y=kx+b的图象经过第一、二、三象限,则k>0,b>0,则kb>0,所以函数y=(kb≠0)的图象经过第一、三象限,故C选项不符合题意;
D、函数y=kx+b的图象经过第二、三、四象限,则k<0,b<0,则kb>0,所以函数y=(kb≠0)的图象经过第一、三象限,故D选项符合题意;
故选:D.
4.解:A、当x=2时,y=﹣3,图象不经过点(2,3),故此选项错误;
B、∵k=﹣6<0,∴图象在二,四象限内,故此选项正确;
C、∵k=﹣6<0,∴在每个象限内,y随x的增大而增大,故此选项错误;
D、当x>﹣1时,则y>6或y<0,故此选项错误;
故选:B.
5.解:∵x2﹣(m﹣1)x+1=0有两个相等的实数根,
∴Δ=[﹣(m﹣1)]2﹣4×1×1=m2﹣2m﹣3=(m﹣3)(m+1)=0,
∴m=3或m=﹣1;
又∵反比例函数y=的图象在每个象限内y随x的增大而增大,
∴m﹣1<0,
∴m<1,
∴m只能为﹣1,
故选:A.
6.解:∵a2+1>0,
∴反比例函数y=(a是常数)的图象在一、三象限,
如图所示,当y1<y2<0<y3时,x3>0>x1>x2,
故选:D.
7.解:∵反比例函数y=﹣中,﹣4<0,
∴双曲线y=﹣的两个分支在第二、四象限.
∵x1<0<x2,
∴A(x1,y1)在第二象限,B(x2,y2)在第四象限.
∴y1>0,y2<0.
∴y1,y2的关系是:y2<0<y1.
故选:A.
8.解:∵菱形的面积为8,
∴S△CDE=2,
∵菱形ABCD的顶点C,D分别在x轴,y轴上,BD∥x轴,
∴S△CDE=|k|,
∴|k|=4,
∵k<0,
∴k=﹣4,
∴该反比例函数的解析式为y=﹣,
故选:B.
9.解:∵在菱形ABOC中,∠A=60°,菱形边长为2,
∴OC=2,∠COB=60°,
过C作CE⊥OB于E,
则∠OCE=30°,
∴OE=OC=1,CE=,
∴点C的坐标为(﹣1,),
∵顶点C在反比例函数y═的图象上,
∴=,得k=﹣,
即y=﹣,
故选:B.
10.解:将A(m,1),B(n,﹣2)代入y2=﹣可得:m=﹣4,n=2,
∴A(﹣4,1),B(2,﹣2),
结合图象可得﹣4<x<0或x>2时y1<y2,
故选:B.
11.解:∵等腰三角形的面积为10,底边长为x,底边上的高为y,
∴xy=10,
∴y与x的函数关系式为:y=.
故选:C.
12.解:由于矩形的另一边长=矩形面积÷一边长,
∴矩形的另一边长y(m)与x的函数关系是y=.
故选:C.
13.解:①当k>0时,y=﹣kx+k过一、二、四象限;y=过一、三象限;
②当k<0时,y=﹣kx+k过一、三、四象象限;y=过二、四象限.
观察图形可知只有A符合.
故选:A.
14.解:过A点作AC⊥OB,
∵AO=AB,AC⊥OB,OB=6,
∴OC=BC=3,
在Rt△AOC中,OA=5,
∵AC=,
∴A(﹣3,4),
把A(﹣3,4)代入y=,可得k=﹣12,
故选:A.
15.解:作BD⊥OA,CE⊥OA,
∵∠BOA=45°,
∴BD=OD,
设B(a,a),
∴,
∴a=3或a=﹣3(舍去),
∴BD=OD=3,
B(3,3),
∵BC=2AC.
∴AB=3AC,
∵BD⊥OA,CE⊥OA,
∴BD∥CE,
.∴△ABD∽△ACE
∵=3,
∴,
∴CE=1,
∵图象经过点C,
∴,
∴x=9,
C(9,1)
设BC的解析式为y=kx+b,
,
解得,
∴x+4,
当x=﹣2019时,y=677,
当x=﹣2020时,y=677,
当x=2021时,y=﹣669,
当x=2022时,y=﹣670,
故选:D.
16.解:由题意得:k2﹣k﹣1=﹣1,且k2+k≠0,
解得:k=1,
故答案为:1.
17.解:∵是反比例函数,
∴1﹣2m≠0,
解得m≠0.5.
故答案为:m≠0.5.
18.解:∵直线y=k1x+b与双曲线y=在同一平面直角坐标系中的图象的交点的横坐标是﹣2和3,
∴关于x的不等式>k1x+b的解集是x<﹣2或0<x<3,
故答案为:x<﹣2或0<x<3.
19.解:反比例函数y=的图象关于y轴对称的函数x互为相反数,y不变.得y==﹣.
故答案为y=﹣.
20.解:正比例函数y=k1x①与反比例函数②的一个交点是(2,3),
∴将(2,3)代入①得k1=,代入②得k2=6,即正比例函数y=x③,反比例函数y=④,
∴x=,解之得x=±2,把x=﹣2代入③得y=﹣3.
∴另一个交点是(﹣2,﹣3).
故答案为:﹣2;﹣3.
21.解:∵一次函数y=ax+b的图象经过第一、三、四象限,
∴a>0,b<0,
∴ab<0,
∴函数y=的图象位于第二、四象限.
故答案为二、四.
22.解:∵反比例函数y=(k为常数),k2+1>0,
∴该函数图象在第一、三象限,在每个象限内y随x的增大而减小,
∵点A(﹣1,y1)、B(﹣,y2)、C(1,y3)都在反比例函数y=(k为常数)的图象上,﹣1<﹣,点A、B在第三象限,点C在第一象限,
∴y2<y1<y3,
故答案为:y2<y1<y3.
23.解:如图,过点A作AD⊥y轴于D,
∵点C是AB的中点,
∴AC=BC,
在△ACD和△BCO中,
,
∴△ACD≌△BCO(AAS),
∴S△ACD=S△BCO=1,CD=OC,
∴S△ADO=2S△ACD=2,
根据反比例函数k的几何意义得|k|=S△AOD=2,
∴|k|=4,
∵k<0,
∴k=﹣4.
故答案为:﹣4.
24.解:∵点A(a,3),B(b,6)在反比例函数y=(x>0)的图象上,
∴k=3a=6b,
∴a=2b,
作AC⊥x轴于C,BD⊥x轴于D,
∵点A(a,3),B(b,6),
∴OC=a=2b,AC=3,OD=b,BD=6,
∵S△AOB=S△BOD+S梯形ABDC﹣S△AOC=S梯形ABDC,S△AOB=9,
∴S梯形ABDC=(AC+BD)(OC﹣OD)=9,
即(3+6)(2b﹣b)=9,
解得b=2,
∴B(2,6),
∴k=2×6=12,
故答案为12.
25.解:∵点A,B均在反比例函数y=的图象上,且点A,B的横坐标分别为1,3,
∴A(1,6),B(3,2),
设直线AB的解析式为y=kx+b,
代入点A,B的坐标可得,
,
解得,
∴直线AB的解析式为y=﹣2x+8,
令y=0,则﹣2x+8=0,
∴x=4,
∴C(4,0),
∴OC=4,
∴S△OAC=6=3OC=12,
故答案为:12.
26.解:连接OC,
∵A在双曲线上,
∴S△AOB=×9=,
又∵AC:AB=2:3,
∴BC:AB=1:3,
∴S△BOC=S△AOB==|k|,
∴k=3(取正值),
故答案为:3.
27.解:∵一元二次方程x2﹣4x+m=0有两个相等的实数根,
∴Δ=16﹣4m=0,
解得m=4.
∵m>0,
∴反比例函数y=的图象在第一三象限,在每个象限内y随x的增大而减小,且第三象限的值总比第一象限的值小.
∵x1<x2<0<x3,
∴y2<y1<0<y3.
故答案为:y2<y1<y3.
28.解:(1)∵S△AOB=4,
∴×2×n=4,解得n=4,
∴B(2,4),
设反比例函数解析式为y=,
把B(2,4)代入得k=2×4=8,
∴反比例函数解析式为y=;
(2)设直线AB的解析式为y=ax+b,
把A(﹣2,0),B(2,4)代入得,解得,
∴直线AB的解析式为y=x+2,
当x=0时,y=x+2=2,则C(0,2),
∴S△OCB=×2×2=2.
故答案为:,(2)2.
29.解:过A作AE⊥x轴于E,过B作BD⊥x轴于D,AC⊥BD于C,
∵∠AOE=45°,AO=,
∴AE=OE=OA=1
在Rt△AOB中,∠A=30°,
∴tan30°==,
设B(a,b),则OD=a,BD=b,
∴AC=1+a,BC=1﹣b,
∵∠ABC=90°,
∴∠ABC+∠OBD=90°,
∵∠OBD+∠BOD=90°,
∴∠ABC=∠BOD,
∵∠BDO=∠ACB=90°,
∴△BOD∽△ABC,
∴,即=,
解得,
∴B(,),
设过点B的反比例函数的解析式为y=,
∴k=×=
∴反比例函数的解析式为y=,
故答案为y=.
30.解:∵矩形的长为x,宽为y,面积为9,
∴xy=9,且x≥3,
则y与x之间的函数关系及定义域是:y=(x≥3).
故答案为:y=(x≥3).
31.解:由题意得:y与x的函数关系式为y==(x>0).
故本题答案为:y=(x>0).
32.解:设反比例函数的表达式为y=,
把(1,200)代入,得:k=200,
∴反比例函数的表达式为y=.
当x=4时,y=50,
∴4月份的利润为50万元.
设一次函数的表达式为y=ax+b,把(4,50),(6,110)代入,得:
,
解得:,
故一次函数的表达式为y=30x﹣70.
当x=9时,y=270﹣70=200(万元),
故9月份的利润为200万元.
故答案为:50,200.
33.解:由正比例函数y=2x与反比例函数y=(k≠0)的图象和性质可知,
其交点A(x1,y1)与B(x2,y2)关于原点对称,
∴y1+y2=0,
故答案为:0.
34.解:∵一元二次方程x2﹣4x+m=0有两个相等的实数根,
∴Δ=16﹣4m=0,
解得m=4,
∵m>0,
∴反比例函数y=图象在一三象限,在每个象限y随x的增大而减少,
∵x1<x2<0,
∴y1>y2,
故答案为>.
35.解:作AM⊥OC,BN⊥OC,
设OM=a,
∵点A在反比例函数y=,
∴AM=,
∵B是AC的中点,
∴AB=BC,
∵AM⊥OC,BN⊥OC,
∴BN∥AM,
∴,,
∴NM=NC,BN==,
∵点B在反比例函数y=,
∴ON=2a,
又∵OM=a,
∴OM=MN=NC=a,
∴OC=3a,
∴S△AOC= OC AM=×3a×=k=12,
解得k=8;
故答案为:8
36.解:(1)A(﹣5,n)B(3,﹣5)都在反比例函数y=的图象上,
∴m=﹣5n=3×(﹣5),
∴m=﹣15,n=3,
∴反比例函数解析式为y=﹣,点A的坐标是(﹣5,3),
将A、B两点坐标代入y=kx+b得,
解得,
∴一次函数的解析式为y=﹣x﹣8;
(2)在y=﹣x﹣8中,令y=0,则x=﹣8,
∴C点坐标(﹣8,0),
∴S△AOB=S△AOC+S△BOC=+=32;
(3)不等式kx+b﹣<0的解集是﹣5<x<0或x>3.
37.解:(1)∵反比例函数y=的图象经过A(1,3),
∴3=,则m=3,
∴反比例函数的表达式为y=,
又∵点B(3,n)在反比例函数y=的图象上.
∴n=1,即B(3,1),
∵一次函数y=kx+b的图象经过A(1,3)、B(3,1)两点.
∴,
解得,
∴一次函数的表达式为y=﹣x+4;
(2)观察图象可知,不等式kx+b≥的解集为x<0或1≤x≤3
(3)设直线y=﹣x+4与y轴交于点C,则C(0,4).
∵S△PAB=S△PBC﹣S△PAC=PC (3﹣1)=4,
∴PC=4,
∴P(0,0)或(0,8).
38.解:(1)如图1,过点A作AD⊥y轴于点D,则∠ADO=∠BOC=90°,
∴BO∥AD,
∴,
∵CB=AB,C(0,﹣8),
∴CO=DO=8,D(0,8),
∵S△OCB=S△OAB=8,
∴×CO×AD=S△OAC=16,
∴×8AD=16,
解得,AD=4,
∴A(4,8),
把A(4,8)代入y=,得8=,
解得,m=32,
把A(4,8)、C(0,﹣8)代入y=kx+b,
得,解得,
∴反比例函数与一次函数的解析式分别为y=和y=4x﹣8.
(2)如图2,设直线y=4x﹣8交双曲线y=的另一个交点是点E,
由得,或,
∴E(﹣2,﹣16),
由函数图象可知,当直线y=4x﹣8在双曲线y=的下方时,则x<﹣2
或0<x<4,
∴不等式kx+b<的解集是x<﹣2
或0<x<4,
由kx+b<得,kx+b﹣<0,
∴kx+b﹣<0的解集是x<﹣2
或0<x<4.
(3)如图3,设点P的坐标为(0,y),则PO=y,DP=8﹣y;
对于直线y=4x﹣8,当y=0时,由4x﹣8=0,得x=2,
∴B(2,0),
过点A作AD⊥y轴于点D,
则∠ADP=∠POB=∠APB=90°,
∴∠APD=90°﹣∠BPO=∠PBO,
∴△ADP∽△POB,
∴,
∴,
解得,y1=,y2=,
∴点P的坐标为(0,)或(0,).
39.解:(1)∵直线y1=k1x+b与双曲线相交于A(﹣2,3),B(m,﹣2)两点,
∴,解得:k2=﹣6,
∴双曲线的表达式为:,
∴把B(m,﹣2)代入,得:,解得:m=3,
∴B(3,﹣2),
把A(﹣2,3)和B(3,﹣2)代入y1=k1x+b得:,
解得:,
∴直线的表达式为:y1=﹣x+1;
(2)过点A作AD⊥BP,交BP的延长线于点D,如图
∵BP∥x轴,
∴AD⊥x轴,BP⊥y轴,
∵A(﹣2,3),B(3,﹣2),
∴BP=3,AD=3﹣(﹣2)=5,
∴;
(3)的解集,则是双曲线的图象在一次函数的图象的上方对应的x的取值,
故其解集为:﹣2<x<0或x>3.
40.解:(1)令y=0,则kx﹣2k=0,
∴x=2,
∴A(2,0),
设C(a,b),
∵CB⊥y轴,
∴B(0,b),
∴BC=﹣a,
∵S△ABC=3,
∴,
∴ab=﹣6,
∴m﹣1=ab=﹣6,
∴m=﹣5,
即A(2,0),m=﹣5;
(2)在Rt△AOB中,AB2=OA2+OB2,
∵,
∴b2+4=8,
∴b2=4,
∴b=±2,
∵b>0,
∴b=2,
∴a=﹣3,
∴C(﹣3,2),
将C(﹣3,2)代入到直线解析式中得,
∴一次函数的表达式为.
一、选择题
1.若函数y=(m2﹣3m+2)x|m|﹣3是反比例函数,则m的值是( )
A.1
B.﹣2
C.2或﹣2
D.2
2.下列关系式中,y是x的反比例函数的是( )
A.y=3x
B.y=5x+1
C.y=﹣x﹣1
D.y=x2﹣3
3.函数y=kx+b与y=(kb≠0)在同一坐标系中的图象可能是图中的( )
A.
B.
C.
D.
4.下列关于反比例函数y=﹣的结论中正确的是( )
A.图象过点(2,3)
B.图象在二、四象限内
C.在每个象限内,y随x的增大而减小
D.当x>﹣1时,y>6
5.已知关于x的方程x2﹣(m﹣1)x+1=0有两个相等的实数根,且反比例函数y=的图象在每个象限内y随x的增大而增大,那么m的值为( )
A.﹣1
B.3或﹣1
C.﹣2
D.3
6.已知点A(x1,y1),B(x2,y2),C(x3,y3)都在反比例函数y=(a是常数)的图象上,且y1<y2<0<y3,则x1,x2,x3的大小关系为( )
A.x2>x1>x3
B.x1>x2>x3
C.x3>x2>x1
D.x3>x1>x2
7.已知点A(x1,y1),B(x2,y2)都在反比例函数y=﹣的图象上,且x1<0<x2,则y1,y2的关系是( )
A.y2<0<y1
B.0<y2<y1
C.y1<y2<0
D.y1<0<y2
8.如图,菱形ABCD的顶点C,D分别在x轴,y轴上,BD∥x轴,反比例函数y=(x<0)的图象过菱形的对称中心E,若菱形的面积为8,则该反比例函数的解析式为( )
A.y=
B.y=﹣
C.y=
D.y=﹣
9.如图,在菱形ABOC中,AB=2,∠A=60°,菱形的一个顶点C在反比例函数y═(k≠0)的图象上,则反比例函数的解析式为( )
A.y=﹣
B.y=﹣
C.y=﹣
D.y=
10.如图,一次函数y1=ax+b和反比例函数y2=﹣的图象交于A(m,1),B(n,﹣2)两点,若当y1<y2时,则x的取值范围是( )
A.x<﹣4或0<x<2
B.﹣4<x<0或x>2
C.﹣2<x<0或x>1
D.x<﹣2或x>1
11.如果等腰三角形的面积为10,底边长为x,底边上的高为y,则y与x的函数关系式为( )
A.y=
B.y=
C.y=
D.y=
12.矩形面积是40m2,设它的一边长为x(m),则矩形的另一边长y(m)与x的函数关系是( )
A.y=20﹣x
B.y=40x
C.y=
D.y=
13.函数y=﹣kx+k和函数y=在同一坐标系内的图象可能是( )
A.B.C.D.
14.如图,O是坐标原点,点B在x轴上,在△OAB中,AO=AB=5,OB=6,点A在反比例函数y=(k≠0)图象上,则k的值( )
A.﹣12
B.﹣15
C.﹣20
D.﹣30
15.如图,在△OAB中,∠BOA=45°,点C为边AB上一点,且BC=2AC.如果函数y=(x>0)的图象经过点B和点C,那么用下列坐标表示的点,在直线BC上的是( )
A.(﹣2019,674)
B.(﹣2020,675)
C.(2021,﹣669)
D.(2022,﹣670)
二、填空题
16.已知函数y=(k2+k)x是反比例函数,则k的值为
.
17.若是反比例函数,则m满足的条件是
.
18.直线y=k1x+b与双曲线y=在同一平面直角坐标系中的图象如图所示,则关于x的不等式>k1x+b的解集为
.
19.已知一个函数的图象与反比例函数y=的图象关于y轴对称,则这个函数的表达式是
.
20.已知正比例函数y=k1x与反比例函数y=的一个交点是(2,3),则另一个交点是(
,
).
21.若一次函数y=ax+b的图象经过第一、三、四象限,则函数y=的图象位于第
象限.
22.若点A(﹣1,y1)、B(﹣,y2)、C(1,y3)都在反比例函数y=(k为常数)的图象上,则y1、y2、y3的大小关系为
.
23.如图,位于第二象限的点A在反比例函数y=图象上,点B在x轴的正半轴上,连接AB交y轴于点C.若点C是AB的中点,且△OCB的面积为1,则k的值为
.
24.如图,点A(a,3),B(b,6)在反比例函数y=(x>0)的图象上,△AOB的面积S△AOB=9,则k的值为
.
25.如图,反比例函数y=在第一象限的图象上有两点A、B,它们的横坐标分别为1、3,直线AB与x轴交于点C,则△OAC的面积为
.
26.如图,点A在双曲线上,过点A作AB⊥x轴于点B,点C在线段AB上且AC:AB=2:3,双曲线经过点C,则k的值为
.
27.一元二次方程x2﹣4x+m=0有两个相等的实数根,点A(x1,y1)、B(x2,y2)、C(x3,y3)是反比例函数y=上的三个点,若x1<x2<0<x3,则y1、y2、y3由大到小为
.
28.如图,在平面直角坐标系xOy中,直线AB与x轴交于点A(﹣2,0),与反比例函数在第一象限内的图象的交于点B(2,n),连接BO,若S△AOB=4.
(1)反比例函数的解析式为
;
(2)若直线AB与y轴的交点为C,则△OCB的面积为
.
29.如图,在平面直角坐标系中,Rt△AOB的斜边AO与x轴负半轴的夹角为45°,若∠A=30°,AO=,则过点B的反比例函数的解析式为
.
30.矩形的长为x,宽为y,面积为9,则y与x之间的函数关系及定义域是
.
31.已知一菱形的面积为12cm2,对角线长分别为xcm和ycm,则y与x的函数关系式为
32.为了响应“绿水青山就是金山银山”的号召,建设生态文明,某工厂自2020年1月开始限产进行治污改造,其月利润y(万元)与月份x(月)之间的变化关系如图所示,治污完成前是反比例函数图象的一部分,治污完成后是一次函数图象的一部分,则4月份的利润为
万元,9月份的利润为
万元.
33.在平面直角坐标系中,一次函数y=2x与反比例函数y=(k≠0)的图象交于A(x1,y1),B(x2,y2)两点,则y1+y2的值是
.
34.一元二次方程x2﹣4x+m=0有两个相等的实数根,点A(x1,y1)、B(x2,y2)是反比例函数y=上的两个点,若x1<x2<0,则y1
y2(填“<”或“>”或“=”).
35.如图,点A、B在反比例函数y=(x>0)的图象上,延长AB交x轴于C点,若△AOC的面积是12,且点B是AC的中点,则k=
.
三、解答题
36.如图,已知A(﹣5,n),B(3,﹣5)是一次函数y=kx+b的图象和反比例函数y=的图象的两个交点.
(1)求反比例函数和一次函数的解析式;
(2)求△AOB的面积;
(3)结合图象,直接写出不等式kx+b﹣<0的解集.
37.如图,一次函数y=kx+b的图象与反比例函数y=的图象交于点A(1,3),B(3,n).
(1)求这两个函数的表达式;
(2)请结合图象直接写出不等式kx+b≥的解集;
(3)若点P为y轴上一点,△PAB的面积为4,求点P的坐标.
38.已知一次函数y=kx+b的图象与反比例函数y=的图象在第一象限交于点A,与x轴交于点B,与y轴交于点C(0,﹣8),若CB=AB,且S△OAB=8.
(1)求反比例函数与一次函数的解析式;
(2)直接写出kx+b﹣<0的解集;
(3)若点P为y轴上一点,求使∠APB=90°的点P的坐标.
39.如图,在平面直角坐标系中,直线y1=k1x+b与双曲线y2=相交于A(﹣2,3),B(m,﹣2)两点.
(1)求y1,y2对应的函数表达式;
(2)过点B作BP∥x轴交y轴于点P,求△ABP的面积;
(3)根据函数图象,直接写出关于x的不等式k1x+b<的解集.
40.如图,一次函数y=kx﹣2k(k≠0)的图象与反比例函数y=(m﹣1≠0)的图象交于点C,与x轴交于点A,过点C作CB⊥y轴,垂足为B,若S△ABC=3.
(1)求点A的坐标及m的值;
(2)若AB=2,求一次函数的表达式.
参考答案
1.解:∵函数y=(m2﹣3m+2)x|m|﹣3是反比例函数,
∴|m|﹣3=﹣1,且m2﹣3m+2≠0,
∴m=±2,
当m=2时,m2﹣3m+2=0,不合题意舍去,
当m=﹣2时,m2﹣3m+2=12≠0,
∴m=﹣2,
故选:B.
2.解:A.是正比例函数,不是反比例函数,故本选项不符合题意;
B.是一次函数,不是反比例函数,故本选项不符合题意;
C.是反比例函数,故本选项符合题意;
D.是二次函数,不是反比例函数,故本选项不符合题意;
故选:C.
3.解:A、函数y=kx+b的图象经过第一、二、四象限,则k<0,b>0,则kb<0,所以函数y=(kb≠0)的图象经过第二、四象限,故A选项不符合题意;
B、函数y=kx+b的图象经过第二、三、四象限,则k<0,b<0,则kb>0,所以函数y=(kb≠0)的图象经过第一、三象限,故B选项不符合题意;
C、函数y=kx+b的图象经过第一、二、三象限,则k>0,b>0,则kb>0,所以函数y=(kb≠0)的图象经过第一、三象限,故C选项不符合题意;
D、函数y=kx+b的图象经过第二、三、四象限,则k<0,b<0,则kb>0,所以函数y=(kb≠0)的图象经过第一、三象限,故D选项符合题意;
故选:D.
4.解:A、当x=2时,y=﹣3,图象不经过点(2,3),故此选项错误;
B、∵k=﹣6<0,∴图象在二,四象限内,故此选项正确;
C、∵k=﹣6<0,∴在每个象限内,y随x的增大而增大,故此选项错误;
D、当x>﹣1时,则y>6或y<0,故此选项错误;
故选:B.
5.解:∵x2﹣(m﹣1)x+1=0有两个相等的实数根,
∴Δ=[﹣(m﹣1)]2﹣4×1×1=m2﹣2m﹣3=(m﹣3)(m+1)=0,
∴m=3或m=﹣1;
又∵反比例函数y=的图象在每个象限内y随x的增大而增大,
∴m﹣1<0,
∴m<1,
∴m只能为﹣1,
故选:A.
6.解:∵a2+1>0,
∴反比例函数y=(a是常数)的图象在一、三象限,
如图所示,当y1<y2<0<y3时,x3>0>x1>x2,
故选:D.
7.解:∵反比例函数y=﹣中,﹣4<0,
∴双曲线y=﹣的两个分支在第二、四象限.
∵x1<0<x2,
∴A(x1,y1)在第二象限,B(x2,y2)在第四象限.
∴y1>0,y2<0.
∴y1,y2的关系是:y2<0<y1.
故选:A.
8.解:∵菱形的面积为8,
∴S△CDE=2,
∵菱形ABCD的顶点C,D分别在x轴,y轴上,BD∥x轴,
∴S△CDE=|k|,
∴|k|=4,
∵k<0,
∴k=﹣4,
∴该反比例函数的解析式为y=﹣,
故选:B.
9.解:∵在菱形ABOC中,∠A=60°,菱形边长为2,
∴OC=2,∠COB=60°,
过C作CE⊥OB于E,
则∠OCE=30°,
∴OE=OC=1,CE=,
∴点C的坐标为(﹣1,),
∵顶点C在反比例函数y═的图象上,
∴=,得k=﹣,
即y=﹣,
故选:B.
10.解:将A(m,1),B(n,﹣2)代入y2=﹣可得:m=﹣4,n=2,
∴A(﹣4,1),B(2,﹣2),
结合图象可得﹣4<x<0或x>2时y1<y2,
故选:B.
11.解:∵等腰三角形的面积为10,底边长为x,底边上的高为y,
∴xy=10,
∴y与x的函数关系式为:y=.
故选:C.
12.解:由于矩形的另一边长=矩形面积÷一边长,
∴矩形的另一边长y(m)与x的函数关系是y=.
故选:C.
13.解:①当k>0时,y=﹣kx+k过一、二、四象限;y=过一、三象限;
②当k<0时,y=﹣kx+k过一、三、四象象限;y=过二、四象限.
观察图形可知只有A符合.
故选:A.
14.解:过A点作AC⊥OB,
∵AO=AB,AC⊥OB,OB=6,
∴OC=BC=3,
在Rt△AOC中,OA=5,
∵AC=,
∴A(﹣3,4),
把A(﹣3,4)代入y=,可得k=﹣12,
故选:A.
15.解:作BD⊥OA,CE⊥OA,
∵∠BOA=45°,
∴BD=OD,
设B(a,a),
∴,
∴a=3或a=﹣3(舍去),
∴BD=OD=3,
B(3,3),
∵BC=2AC.
∴AB=3AC,
∵BD⊥OA,CE⊥OA,
∴BD∥CE,
.∴△ABD∽△ACE
∵=3,
∴,
∴CE=1,
∵图象经过点C,
∴,
∴x=9,
C(9,1)
设BC的解析式为y=kx+b,
,
解得,
∴x+4,
当x=﹣2019时,y=677,
当x=﹣2020时,y=677,
当x=2021时,y=﹣669,
当x=2022时,y=﹣670,
故选:D.
16.解:由题意得:k2﹣k﹣1=﹣1,且k2+k≠0,
解得:k=1,
故答案为:1.
17.解:∵是反比例函数,
∴1﹣2m≠0,
解得m≠0.5.
故答案为:m≠0.5.
18.解:∵直线y=k1x+b与双曲线y=在同一平面直角坐标系中的图象的交点的横坐标是﹣2和3,
∴关于x的不等式>k1x+b的解集是x<﹣2或0<x<3,
故答案为:x<﹣2或0<x<3.
19.解:反比例函数y=的图象关于y轴对称的函数x互为相反数,y不变.得y==﹣.
故答案为y=﹣.
20.解:正比例函数y=k1x①与反比例函数②的一个交点是(2,3),
∴将(2,3)代入①得k1=,代入②得k2=6,即正比例函数y=x③,反比例函数y=④,
∴x=,解之得x=±2,把x=﹣2代入③得y=﹣3.
∴另一个交点是(﹣2,﹣3).
故答案为:﹣2;﹣3.
21.解:∵一次函数y=ax+b的图象经过第一、三、四象限,
∴a>0,b<0,
∴ab<0,
∴函数y=的图象位于第二、四象限.
故答案为二、四.
22.解:∵反比例函数y=(k为常数),k2+1>0,
∴该函数图象在第一、三象限,在每个象限内y随x的增大而减小,
∵点A(﹣1,y1)、B(﹣,y2)、C(1,y3)都在反比例函数y=(k为常数)的图象上,﹣1<﹣,点A、B在第三象限,点C在第一象限,
∴y2<y1<y3,
故答案为:y2<y1<y3.
23.解:如图,过点A作AD⊥y轴于D,
∵点C是AB的中点,
∴AC=BC,
在△ACD和△BCO中,
,
∴△ACD≌△BCO(AAS),
∴S△ACD=S△BCO=1,CD=OC,
∴S△ADO=2S△ACD=2,
根据反比例函数k的几何意义得|k|=S△AOD=2,
∴|k|=4,
∵k<0,
∴k=﹣4.
故答案为:﹣4.
24.解:∵点A(a,3),B(b,6)在反比例函数y=(x>0)的图象上,
∴k=3a=6b,
∴a=2b,
作AC⊥x轴于C,BD⊥x轴于D,
∵点A(a,3),B(b,6),
∴OC=a=2b,AC=3,OD=b,BD=6,
∵S△AOB=S△BOD+S梯形ABDC﹣S△AOC=S梯形ABDC,S△AOB=9,
∴S梯形ABDC=(AC+BD)(OC﹣OD)=9,
即(3+6)(2b﹣b)=9,
解得b=2,
∴B(2,6),
∴k=2×6=12,
故答案为12.
25.解:∵点A,B均在反比例函数y=的图象上,且点A,B的横坐标分别为1,3,
∴A(1,6),B(3,2),
设直线AB的解析式为y=kx+b,
代入点A,B的坐标可得,
,
解得,
∴直线AB的解析式为y=﹣2x+8,
令y=0,则﹣2x+8=0,
∴x=4,
∴C(4,0),
∴OC=4,
∴S△OAC=6=3OC=12,
故答案为:12.
26.解:连接OC,
∵A在双曲线上,
∴S△AOB=×9=,
又∵AC:AB=2:3,
∴BC:AB=1:3,
∴S△BOC=S△AOB==|k|,
∴k=3(取正值),
故答案为:3.
27.解:∵一元二次方程x2﹣4x+m=0有两个相等的实数根,
∴Δ=16﹣4m=0,
解得m=4.
∵m>0,
∴反比例函数y=的图象在第一三象限,在每个象限内y随x的增大而减小,且第三象限的值总比第一象限的值小.
∵x1<x2<0<x3,
∴y2<y1<0<y3.
故答案为:y2<y1<y3.
28.解:(1)∵S△AOB=4,
∴×2×n=4,解得n=4,
∴B(2,4),
设反比例函数解析式为y=,
把B(2,4)代入得k=2×4=8,
∴反比例函数解析式为y=;
(2)设直线AB的解析式为y=ax+b,
把A(﹣2,0),B(2,4)代入得,解得,
∴直线AB的解析式为y=x+2,
当x=0时,y=x+2=2,则C(0,2),
∴S△OCB=×2×2=2.
故答案为:,(2)2.
29.解:过A作AE⊥x轴于E,过B作BD⊥x轴于D,AC⊥BD于C,
∵∠AOE=45°,AO=,
∴AE=OE=OA=1
在Rt△AOB中,∠A=30°,
∴tan30°==,
设B(a,b),则OD=a,BD=b,
∴AC=1+a,BC=1﹣b,
∵∠ABC=90°,
∴∠ABC+∠OBD=90°,
∵∠OBD+∠BOD=90°,
∴∠ABC=∠BOD,
∵∠BDO=∠ACB=90°,
∴△BOD∽△ABC,
∴,即=,
解得,
∴B(,),
设过点B的反比例函数的解析式为y=,
∴k=×=
∴反比例函数的解析式为y=,
故答案为y=.
30.解:∵矩形的长为x,宽为y,面积为9,
∴xy=9,且x≥3,
则y与x之间的函数关系及定义域是:y=(x≥3).
故答案为:y=(x≥3).
31.解:由题意得:y与x的函数关系式为y==(x>0).
故本题答案为:y=(x>0).
32.解:设反比例函数的表达式为y=,
把(1,200)代入,得:k=200,
∴反比例函数的表达式为y=.
当x=4时,y=50,
∴4月份的利润为50万元.
设一次函数的表达式为y=ax+b,把(4,50),(6,110)代入,得:
,
解得:,
故一次函数的表达式为y=30x﹣70.
当x=9时,y=270﹣70=200(万元),
故9月份的利润为200万元.
故答案为:50,200.
33.解:由正比例函数y=2x与反比例函数y=(k≠0)的图象和性质可知,
其交点A(x1,y1)与B(x2,y2)关于原点对称,
∴y1+y2=0,
故答案为:0.
34.解:∵一元二次方程x2﹣4x+m=0有两个相等的实数根,
∴Δ=16﹣4m=0,
解得m=4,
∵m>0,
∴反比例函数y=图象在一三象限,在每个象限y随x的增大而减少,
∵x1<x2<0,
∴y1>y2,
故答案为>.
35.解:作AM⊥OC,BN⊥OC,
设OM=a,
∵点A在反比例函数y=,
∴AM=,
∵B是AC的中点,
∴AB=BC,
∵AM⊥OC,BN⊥OC,
∴BN∥AM,
∴,,
∴NM=NC,BN==,
∵点B在反比例函数y=,
∴ON=2a,
又∵OM=a,
∴OM=MN=NC=a,
∴OC=3a,
∴S△AOC= OC AM=×3a×=k=12,
解得k=8;
故答案为:8
36.解:(1)A(﹣5,n)B(3,﹣5)都在反比例函数y=的图象上,
∴m=﹣5n=3×(﹣5),
∴m=﹣15,n=3,
∴反比例函数解析式为y=﹣,点A的坐标是(﹣5,3),
将A、B两点坐标代入y=kx+b得,
解得,
∴一次函数的解析式为y=﹣x﹣8;
(2)在y=﹣x﹣8中,令y=0,则x=﹣8,
∴C点坐标(﹣8,0),
∴S△AOB=S△AOC+S△BOC=+=32;
(3)不等式kx+b﹣<0的解集是﹣5<x<0或x>3.
37.解:(1)∵反比例函数y=的图象经过A(1,3),
∴3=,则m=3,
∴反比例函数的表达式为y=,
又∵点B(3,n)在反比例函数y=的图象上.
∴n=1,即B(3,1),
∵一次函数y=kx+b的图象经过A(1,3)、B(3,1)两点.
∴,
解得,
∴一次函数的表达式为y=﹣x+4;
(2)观察图象可知,不等式kx+b≥的解集为x<0或1≤x≤3
(3)设直线y=﹣x+4与y轴交于点C,则C(0,4).
∵S△PAB=S△PBC﹣S△PAC=PC (3﹣1)=4,
∴PC=4,
∴P(0,0)或(0,8).
38.解:(1)如图1,过点A作AD⊥y轴于点D,则∠ADO=∠BOC=90°,
∴BO∥AD,
∴,
∵CB=AB,C(0,﹣8),
∴CO=DO=8,D(0,8),
∵S△OCB=S△OAB=8,
∴×CO×AD=S△OAC=16,
∴×8AD=16,
解得,AD=4,
∴A(4,8),
把A(4,8)代入y=,得8=,
解得,m=32,
把A(4,8)、C(0,﹣8)代入y=kx+b,
得,解得,
∴反比例函数与一次函数的解析式分别为y=和y=4x﹣8.
(2)如图2,设直线y=4x﹣8交双曲线y=的另一个交点是点E,
由得,或,
∴E(﹣2,﹣16),
由函数图象可知,当直线y=4x﹣8在双曲线y=的下方时,则x<﹣2
或0<x<4,
∴不等式kx+b<的解集是x<﹣2
或0<x<4,
由kx+b<得,kx+b﹣<0,
∴kx+b﹣<0的解集是x<﹣2
或0<x<4.
(3)如图3,设点P的坐标为(0,y),则PO=y,DP=8﹣y;
对于直线y=4x﹣8,当y=0时,由4x﹣8=0,得x=2,
∴B(2,0),
过点A作AD⊥y轴于点D,
则∠ADP=∠POB=∠APB=90°,
∴∠APD=90°﹣∠BPO=∠PBO,
∴△ADP∽△POB,
∴,
∴,
解得,y1=,y2=,
∴点P的坐标为(0,)或(0,).
39.解:(1)∵直线y1=k1x+b与双曲线相交于A(﹣2,3),B(m,﹣2)两点,
∴,解得:k2=﹣6,
∴双曲线的表达式为:,
∴把B(m,﹣2)代入,得:,解得:m=3,
∴B(3,﹣2),
把A(﹣2,3)和B(3,﹣2)代入y1=k1x+b得:,
解得:,
∴直线的表达式为:y1=﹣x+1;
(2)过点A作AD⊥BP,交BP的延长线于点D,如图
∵BP∥x轴,
∴AD⊥x轴,BP⊥y轴,
∵A(﹣2,3),B(3,﹣2),
∴BP=3,AD=3﹣(﹣2)=5,
∴;
(3)的解集,则是双曲线的图象在一次函数的图象的上方对应的x的取值,
故其解集为:﹣2<x<0或x>3.
40.解:(1)令y=0,则kx﹣2k=0,
∴x=2,
∴A(2,0),
设C(a,b),
∵CB⊥y轴,
∴B(0,b),
∴BC=﹣a,
∵S△ABC=3,
∴,
∴ab=﹣6,
∴m﹣1=ab=﹣6,
∴m=﹣5,
即A(2,0),m=﹣5;
(2)在Rt△AOB中,AB2=OA2+OB2,
∵,
∴b2+4=8,
∴b2=4,
∴b=±2,
∵b>0,
∴b=2,
∴a=﹣3,
∴C(﹣3,2),
将C(﹣3,2)代入到直线解析式中得,
∴一次函数的表达式为.
