人教版数学九年级上册第23章旋转几何证明题提高篇(word版、含答案)
文档属性
| 名称 | 人教版数学九年级上册第23章旋转几何证明题提高篇(word版、含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 472.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-05 09:14:10 | ||
图片预览


文档简介
人教版数学九年级上册
第二十三章旋转几何证明题提高篇1(含答案)
如图1,已知∠DAC=90°,△ABC是等边三角形,点P为射线AD上任意一点(点P与点A不重合),连结CP,将线段CP绕点C顺时针旋转60°得到线段CQ,连结QB并延长交直线AD于点E.
(1)如图1,猜想∠QEP=______°;
(2)如图2,3,若当∠DAC是锐角或钝角时,其它条件不变,猜想∠QEP的度数,选取一种情况加以证明;
(3)如图3,若∠DAC=135°,∠ACP=15°,且AC=4,求BQ的长.
如图1,在Rt△ABC中,∠A=90°,AB=AC,点D,E分别在边AB,AC上,AD=AE,连接DC,点M,P,N分别为DE,DC,BC的中点.
(1)观察猜想:
图1中,线段PM与PN的数量关系是______,位置关系是______;
(2)探究证明:
把△ADE绕点A逆时针方向旋转到图2的位置,连接MN,BD,CE,判断△PMN的形状,并说明理由;
(3)拓展延伸:
把△ADE绕点A在平面内自由旋转,若AD=4,AB=10,请直接写出△PMN面积的最大值.
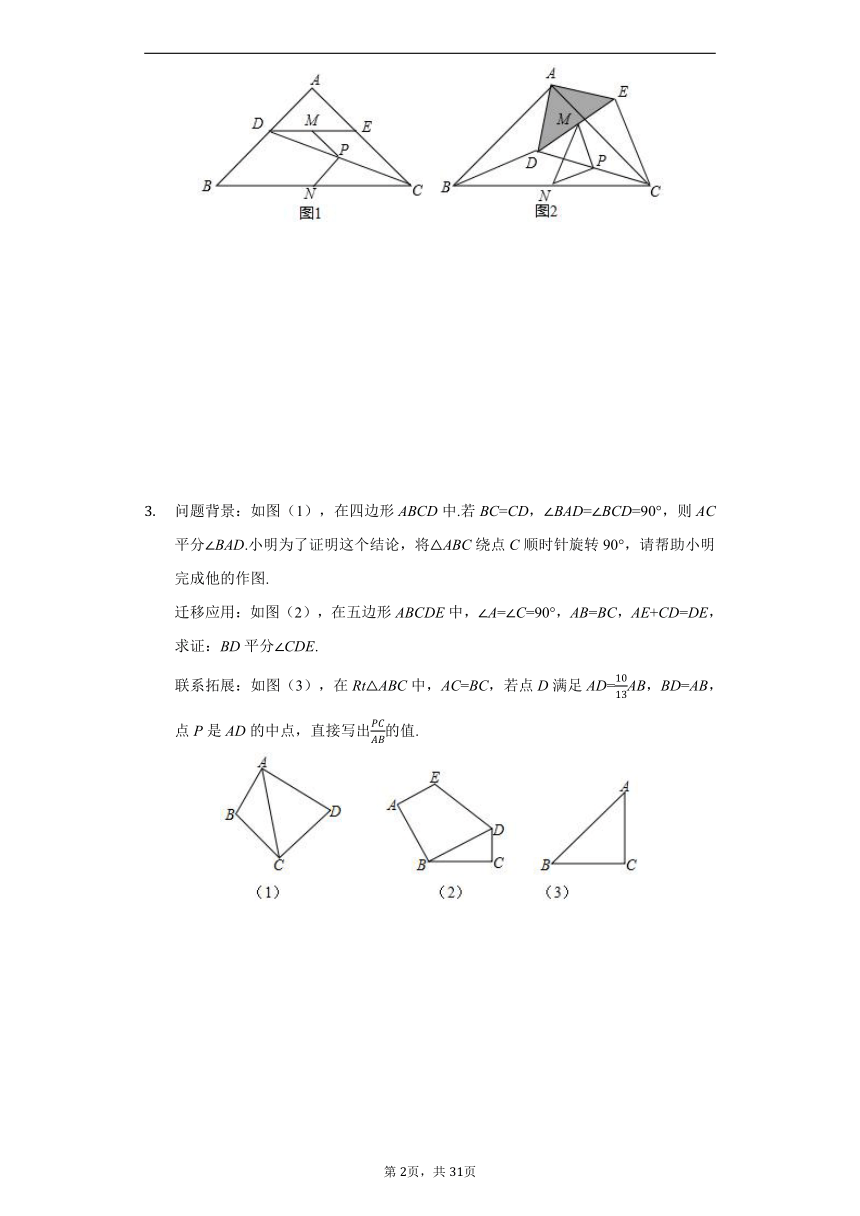
问题背景:如图(1),在四边形ABCD中.若BC=CD,∠BAD=∠BCD=90°,则AC平分∠BAD.小明为了证明这个结论,将△ABC绕点C顺时针旋转90°,请帮助小明完成他的作图.
迁移应用:如图(2),在五边形ABCDE中,∠A=∠C=90°,AB=BC,AE+CD=DE,求证:BD平分∠CDE.
联系拓展:如图(3),在Rt△ABC中,AC=BC,若点D满足AD=AB,BD=AB,点P是AD的中点,直接写出的值.
如图,点A是线段BC上一点,ABD和ACE都是等边三角形.
(1)如图,连接BE,CD,求证:BE=CD.
(2)如图,将ABD绕点A顺时针旋转得到AB'D'.
当旋转角为 度时,边AD'落在边AE上.
在的条件下,延长DD'交CE于点P,连接BD',CD',当线段AB,AC满足什么数量关系时,BDD'与CPD'全等 并给予证明.
已知ABC中,AB=AC,D,E是BC边上的点,将ABD绕点A旋转,得到ACD',连接D'E.
(1)如图,当BAC=,DAE=时,求证:DE=D'E.
(2)如图,当DE=D'E时,DAE与BAC有怎样的数量关系,并说明理由.
(3)如图,在(2)的条件下,当BAC=,BD与DE满足怎样的数量关系时,D'EC是等腰直角三角形 (直接写出结论,不必说明理由)
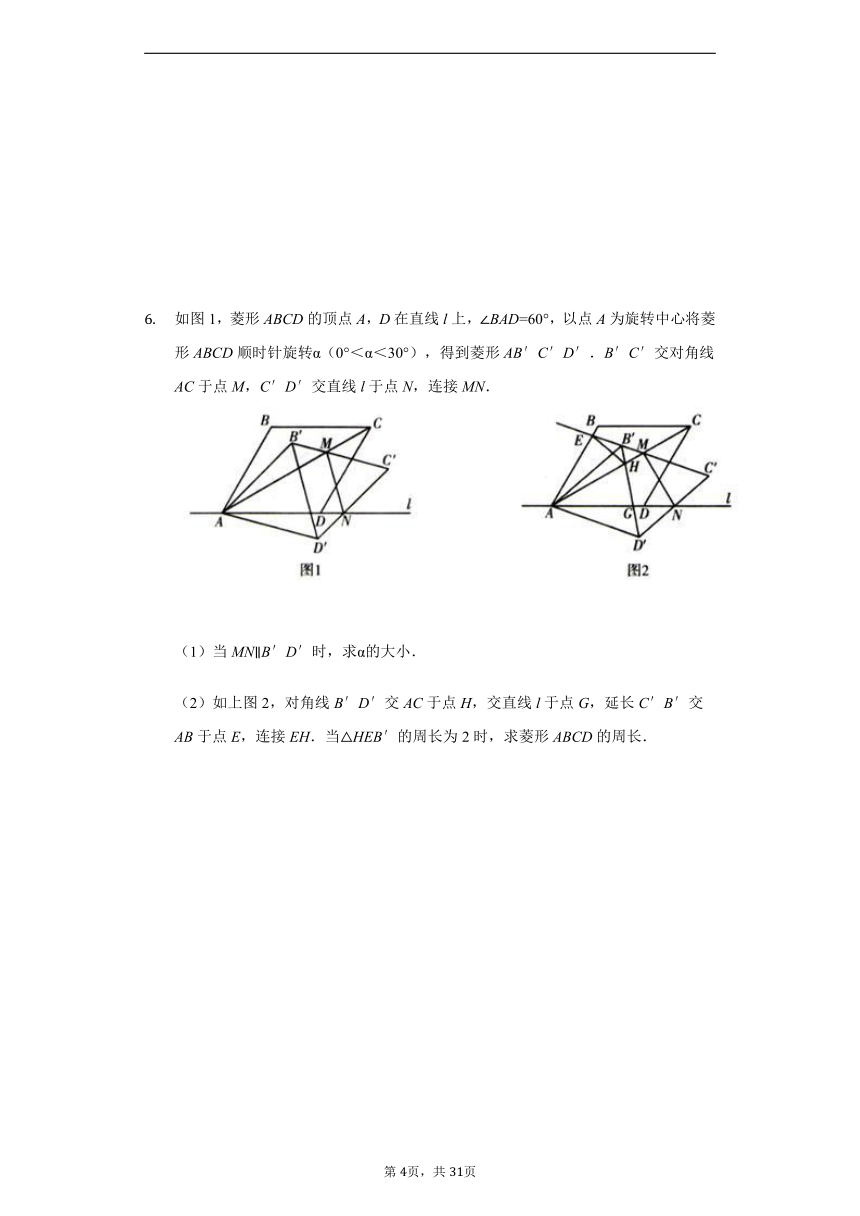
如图1,菱形ABCD的顶点A,D在直线l上,∠BAD=60°,以点A为旋转中心将菱形ABCD顺时针旋转α(0°<α<30°),得到菱形AB′C′D′.B′C′交对角线AC于点M,C′D′交直线l于点N,连接MN.
(1)当MN∥B′D′时,求α的大小.
(2)如上图2,对角线B′D′交AC于点H,交直线l于点G,延长C′B′交AB于点E,连接EH.当△HEB′的周长为2时,求菱形ABCD的周长.
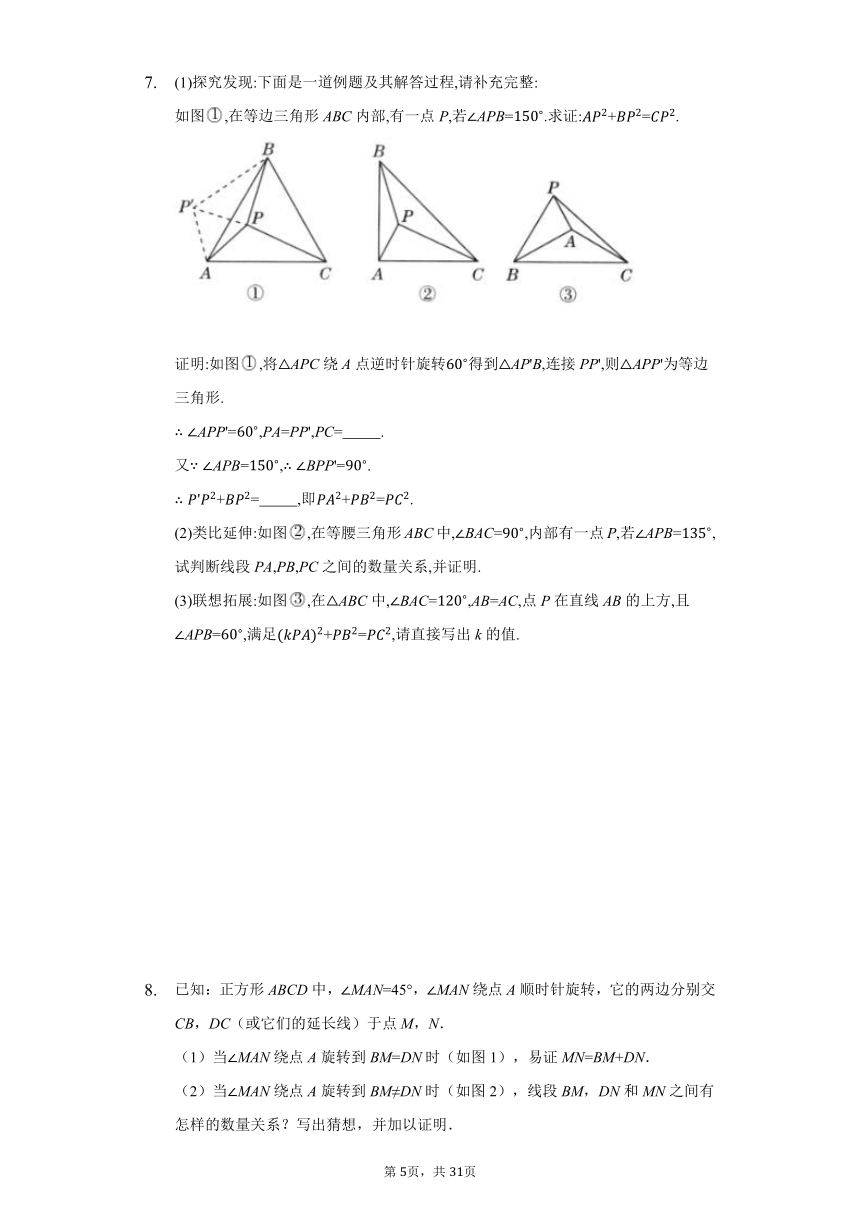
(1)探究发现:下面是一道例题及其解答过程,请补充完整:
如图,在等边三角形ABC内部,有一点P,若APB=.求证:+=.
证明:如图,将APC绕A点逆时针旋转得到AP'B,连接PP',则APP'为等边三角形.
APP'=,PA=PP',PC= .
又APB=,BPP'=.
+= ,即+=.
(2)类比延伸:如图,在等腰三角形ABC中,BAC=,内部有一点P,若APB=,试判断线段PA,PB,PC之间的数量关系,并证明.
(3)联想拓展:如图,在ABC中,BAC=,AB=AC,点P在直线AB的上方,且APB=,满足+=,请直接写出k的值.
已知:正方形ABCD中,∠MAN=45°,∠MAN绕点A顺时针旋转,它的两边分别交CB,DC(或它们的延长线)于点M,N.
(1)当∠MAN绕点A旋转到BM=DN时(如图1),易证MN=BM+DN.
(2)当∠MAN绕点A旋转到BM≠DN时(如图2),线段BM,DN和MN之间有怎样的数量关系?写出猜想,并加以证明.
(3)当∠MAN绕点A旋转到如图3的位置时,线段BM,DN和MN之间又有怎样的数量关系?写出猜想,并加以证明.
如图1,将两个完全相同的三角形纸片ABC和DEC重合放置,其中∠C=90°,∠B=∠E=30°.
(1)操作发现:
如图2,固定△ABC,使△DEC绕点C旋转,当点D恰好落在AB边上时,填空:
①线段DE与AC的位置关系是______;
②设△BDC的面积为S1,△AEC的面积为S2,则S1与S2的数量关系是______.
(2)猜想论证:
当△DEC绕点C旋转到如图3所示的位置时,小明猜想(1)中S1与S2的数量关系仍然成立,并尝试分别作出了△BDC和△AEC中BC、CE边上的高,请你证明小明的猜想.
(3)拓展探究
已知∠ABC=60°,点D是角平分线上一点,BD=CD=6,DE∥AB交BC于点E(如图4),若在射线BA上存在点F,使S△DCF=S△BDE,请求出相应的BF的长.
在Rt△ABC中,∠BCA=90°,∠A<∠ABC,D是AC边上一点,且DA=DB,O是AB的中点,CE是△BCD的中线.
(1)如图a,连接OC,请直接写出∠OCE和∠OAC的数量关系:______;
(2)点M是射线EC上的一个动点,将射线OM绕点O逆时针旋转得射线ON,使∠MON=∠ADB,ON与射线CA交于点N.
①如图b,猜想并证明线段OM和线段ON之间的数量关系;
②若∠BAC=30°,BC=m,当∠AON=15°时,请直接写出线段ME的长度(用含m的代数式表示).
如图①,在Rt△ABC中.∠ABC=90°.将△ABC绕点C顺时针旋转一定的角度得到△DEC.连接AD、BE.并延长BE交AD于点F.
(1)求证:∠DEF=∠ABF;
(2)求证:AF=DF;
(3)当EC⊥BC时,如图②,若AC=5,BC=3.求EF的长.
如图,点P是等边△ABC内一点,且∠BPC=120°,点M是边BC的中点,连接PA,PM.
(1)如图1,若点A,P,M三点共线,则AP与PM的数量关系是______
(2)如图2,若点A,P,M三点不共线,问(1)中的结论还成立吗?若成立,请给出证明,若不成立,请说明理由;
(3)如图3,若AB=2,=,直接写出AP的长是______.
如图1,在Rt△ABC中,∠B=90°,AB=4,BC=2,点D、E分别是边BC、AC的中点,连接DE.将△CDE绕点C逆时针方向旋转,记旋转角为α.
(1)问题发现
①当α=0°时,=______;②当α=180°时,=______.
(2)拓展探究
试判断:当0°≤α<360°时,的大小有无变化?请仅就图2的情形给出证明.
(3)问题解决
△CDE绕点C逆时针旋转至A、B、E三点在同一条直线上时,求线段BD的长.
如图1,△ABC中,AB=AC,点D在BC上,点E在AC上,且AE=AD.
(1)求证:∠BAD=2∠CDE;
(2)如图2,过点D作DF⊥AC,垂足为F,若∠CAD=2∠B,求证:AC+AD=2CF;
(3)如图3,在(2)的条件下,把△DCE沿DE翻折得到△DGE,若AG=8,CE=2,求BD的长.
平面直角坐标系中,点A(a,0)、B(0,b),且a、b满足:=-b2+6b-9,点A、C关于y轴对称,点F为x轴上一动点.
(1)求点A、B两点的坐标;
(2)如图1,若BC⊥CD,BA⊥EA,且BD=BE,连接ED交x轴于点M,求证:DM=ME;
(3)如图2,若BC⊥CD,且BC=CD,直线BC上存在某点G(m,3m+3),使△DFG为等腰直角三角形(点D、F,G按逆时针方向排列),请直接写出点F的坐标______.
如图,△ABC和△ECD都是等边三角形,直线AE,BD交于点F.
(1)如图1,当A,C,D三点在同一直线上时,∠AFB的度数为______
,线段AE与BD的数量关系为______
.
(2)如图2,当△ECD绕点C顺时针旋转α(0°≤α<360°)时,(1)中的结论是否还成立?若不成立,请说明理由;若成立,请就图2给予证明.
(3)若AC=4,CD=3,当△ECD绕点C顺时针旋转一周时,请直接写出BD长的取值范围.
在Rt△ACB中,∠ACB=90°,AC=BC,D为AB上一点,连接CD,将CD绕C点逆时针旋转90°至CE,连接DE,过C作CF⊥DE交AB于F,连接BE.
(1)求证:AD=BE;
(2)求线段AD、BF、DF之间的数量关系.
(3)若∠ACD=15°,CD=+1,求BF.
18.已知:∠AOB=∠COD=90°,OA=OB,OC=OD.(OC>OA)
(1)如图1:连AC、BD,判断:AC与BD之间的关系;并说明理由.
(2)若将△COD绕点O逆时针旋转,
①如图2,当点C恰好在AB边上时,请写出AC、BC、OC之间数量关系;并说明理由.
②当点B、D、C在同一条直线上时,若OB=6,OC=5,求AC的长.
1.解:(1)60;
(2)∠QEP=60°.以∠DAC是锐角为例.
证明:如图2,
∵△ABC是等边三角形,
∴AC=BC,∠ACB=60°,
∵线段CP绕点C顺时针旋转60°得到线段CQ,
∴CP=CQ,∠PCQ=6O°,
∴∠ACB+∠BCP=∠BCP+∠PCQ,
即∠ACP=∠BCQ,
在△ACP和△BCQ中,
,
∴△ACP≌△BCQ(SAS),
∴∠APC=∠Q,
∵∠1=∠2,
∴∠QEP=∠PCQ=60°;
(3) 作CH⊥AD于H,如图3,
与(2)一样可证明△ACP≌△BCQ,
∴AP=BQ,
∵∠DAC=135°,∠ACP=15°,
∴∠APC=30°,∠PCB=45°,
∴△ACH为等腰直角三角形,
∴AH=CH=AC=×4=2,
在Rt△PHC中,PH=CH=2,
∴PA=PH-AH=2-2,
∴BQ=2-2.
2.解:(1)PM=PN;PM⊥PN
(2) △PMN是等腰直角三角形.
由旋转知,∠BAD=∠CAE,
∵AB=AC,AD=AE,
∴△ABD≌△ACE(SAS),
∴∠ABD=∠ACE,BD=CE,
利用三角形的中位线得,PN=BD,PM=CE,
∴PM=PN,
∴△PMN是等腰三角形,
同(1)的方法得,PM∥CE,
∴∠DPM=∠DCE,
同(1)的方法得,PN∥BD,
∴∠PNC=∠DBC,
∵∠DPN=∠DCB+∠PNC=∠DCB+∠DBC,
∴∠MPN=∠DPM+∠DPN=∠DCE+∠DCB+∠DBC
=∠BCE+∠DBC=∠ACB+∠ACE+∠DBC
=∠ACB+∠ABD+∠DBC=∠ACB+∠ABC,
∵∠BAC=90°,
∴∠ACB+∠ABC=90°,
∴∠MPN=90°,
∴△PMN是等腰直角三角形;
(3)方法1:如图2,
同(2)的方法得,△PMN是等腰直角三角形,
∴MN最大时,△PMN的面积最大,
∴DE∥BC且DE在顶点A上面,
∴MN最大=AM+AN,
连接AM,AN,
在△ADE中,AD=AE=4,∠DAE=90°,
∴AM=2,
在Rt△ABC中,AB=AC=10,AN=5,
∴MN最大=2+5=7,
∴S△PMN最大=PM2=×MN2=×(7)2=.
方法2:由(2)知,△PMN是等腰直角三角形,PM=PN=BD,
∴PM最大时,△PMN面积最大,
∴点D在BA的延长线上,
∴BD=AB+AD=14,
∴PM=7,
∴S△PMN最大=PM2=×72=.
3.解:问题背景:
如图(1)所示,
作法:延长AD,在AD的延长线上取一点F使DF=AB,连接CF,
即:△CDF是△ABC绕点C顺时针旋转90°所得;
理由:在四边形ABCD中,∠BAD=∠BCD=90°,
∴∠BAD+∠BCD=180°,
∴∠ABC+∠ADC=180°,
∵∠ADC+∠CDF=180°,
∴∠ABC=∠CDF,
∵BC=CD,
∴△ABC≌△FDC(SAS),
∴∠BAC=∠DFC,AC=CF,
∴∠CAF=∠CFD,
∴∠BAC=∠DAC,
即:AC平分∠BAD;
迁移应用:如图(2),
连接BE,延长DC,在DC的延长线上取一点F,使CG=AE,连接BG,
∵∠A=∠BCD=90°,
∴∠BCG=90°=∠A,
∵BC=AB,
∴△BCG≌△BAE(SAS),
∴BG=BE,
∵AE+CD=DE,
∴CG+CD=DE,
即:DG=DE,
∵BD=BD,
∴△BDG≌△BDE(SSS),
∴∠BDG=∠BDE,
∴BD平分∠CDE;
联系拓展:当点D在AB上方时,如图(3),
连接CP,在PB的延长线上取一点Q,使BQ=AP,连接CQ,
设AB=13a,
∵AD=AB,BD=AB,
∴BD=13a,AD=10a,
∵点P是AD的中点,
∴BP=AP=AD=5a,
∵BD=AB,
∴BP⊥AD,
∴∠APD=90°,
∵∠ACB=90°,
∴∠APB+∠ACB=180°,
∴∠CBP+∠CAP=180°,
∵∠CBP+∠CBQ=180°,
∴∠CAP=∠CBQ,
∵AC=BC,
∴△ACP≌△BCQ(SAS),
∴CP=CQ,∠ACP=∠BCG,
∴∠PCQ=∠PCB+∠BCQ=∠PCB+∠ACP=∠ACB=90°,
在Rt△ABP中,根据勾股定理得,BP==12a,
∴PQ=BP+BQ=12a+5a=17a,
在Rt△PCQ中,PC=PQ=a,
∴==,
当点D在AB下方时,如图(4),
∵AB=BD,点P是AD的中点,
∴BP⊥AD,
∴AP=AD,∠BPA=90°=∠ACB,
∴∠CBP=∠CAP,
过点C作CH⊥CP交BP于H,
∴∠PCH=90°=∠ACB,
∴∠BCH=∠ACP,
∴△CBH≌△CAP(ASA),
∴BH=AP,
设AB=m,则AD=m,
∴AP=AD=m,
∴BH=m,
在Rt△APB时,BP==m,
∴PH=BP-BH=m,
∴CP==×m=,
∴==,
即:的值为或.
4.解:(1)证明:ACE,ABD都是等边三角形,
AB=AD,AE=AC,BAD=CAE=.
BAD+DAE=CAE+DAE,即BAE=DAC.
BAEDAC.
BE=CD.
(2)60
当AC=2AB时,BDD'与CPD'全等.
证明:由旋转和等边三角形的知识可知AB=BD=DD'=AD',
四边形ABDD'是菱形,
ABD'=DBD'=ABD=,DPBC.
ACE是等边三角形,
AC=AE=CE,ACE=.
AC=2AB,AE=2AD',
PCD'=ACD'=ACE=.
DPBC,
ABD'=DBD'=BD'D=ACD'=PCD'=PD'C=,
BD'=CD',
BDD'CPD'.
5.解:(1)证明:ABD绕点A旋转得到ACD',
AD=AD',CAD'=BAD.
BAC=,DAE=,
D'AE=CAD'+CAE=BAD+CAE=BAC-DAE=-=.
DAE=D'AE.
在ADE和AD'E中,
ADEAD'E(SAS).
DE=D'E.
(2)解:DAE=BAC.理由如下:
在ADE和AD'E中,
ADEAD'E(SSS).
DAE=D'AE.
BAD+CAE=CAD'+CAE=D'AE=DAE.
DAE=BAC.
(3)解:当DE=BD时,D'EC是等腰直角三角形.
6.解:(1)∵MN∥B′D′易证△C′MN是等边三角形
又∵C′B′=C′D′
∴MB′=ND′
在△AB′M和△AD′N中AB′=AD′,∠AB′M=∠AD′N,B′M=D′N
∴△AB′M △AD′N
∴∠B′AM=∠D′AN
又∵∠D′AN=α
∴∠B′AM=α
∴∠B′AM=∠BAB′=∠BAC=∠BAD=15°
即α=15°;
(2)在△AB′E和△AD′G中,
∠AB′E=∠AD′G,∠EAB′=∠GAD′,AB′=AD′
∴△AB′E △AD′G
∴EB′=GD′,
AE=AG在△AHE和△AHG中,
AE=AG,∠EAH=∠GAH,AH=AH
∴△AHE△AHG
∴EH=GH
∵△HEB′的周长为2
∴EH+EB′+B′H=2
∴GH+GD′+B′H=2
∴B′D′=BD=2
∴菱形ABCD的周长为8.
7.解:(1)BP';
(2)+=.
证明:如图,将APC绕A点逆时针旋转,得到AP'B,连接PP',
则P'A=PA,P'AP=,P'B=PC,
APP'=,=+=.
APB=,
BPP'=.
+=.
+=.
(3)k=±.
8.解:(1)如图1,连接AC,交MN于点G,
∵四边形ABCD为正方形,
∴BC=CD,且BM=DN,
∴CM=CN,且AC平分∠BCD,
∴AC⊥MN,且MG=GN,
∴∠MAG=∠NAG,
∵∠BAC=∠MAN=45°,即∠BAM+∠GAM=∠GAM+∠GAN,
∴∠BAM=∠GAN=∠GAM,
在△ABM和△AGM中,
∴△ABM≌△AGM(AAS),
∴BM=MG,同理可得GN=DN,
∴BM+DN=MG+GN=MN,
∴BM+DN=MN;
(2)猜想:BM+DN=MN,
证明如下:
如图2,在MB的延长线上,截取BE=DN,连接AE,
在△ABE和△ADN中,
∴△ABE≌△ADN(SAS),
∴AE=AN,∠EAB=∠NAD,
∵∠BAD=90°,∠MAN=45°,
∴∠BAM+∠DAN=45°,
∴∠EAB+∠BAM=45°,
∴∠EAM=∠NAM,
在△AEM和△ANM中
∴△AEM≌△ANM(SAS),
∴ME=MN,
又ME=BE+BM=BM+DN,
∴BM+DN=MN;
(3)DN-BM=MN.
证明如下:
如图3,在DC上截取DF=BM,连接AF,
△ABM和△ADF中,,
∴△ABM≌△ADF(SAS),
∴AM=AF,∠BAM=∠DAF,
∴∠BAM+∠BAF=∠BAF+∠DAF=90°,即∠MAF=∠BAD=90°,
∵∠MAN=45°,
∴∠MAN=∠FAN=45°,
在△MAN和△FAN中,
∴△MAN≌△FAN(SAS),
∴MN=NF,
∴MN=DN-DF=DN-BM,
∴DN-BM=MN.
9.(1)①DE∥AC,②S1=S2
;
(2)如图3中,
∵△DEC是由△ABC绕点C旋转得到,
∴BC=CE,AC=CD,
∵∠ACN+∠BCN=90°,∠DCM+∠BCN=180°-90°=90°,
∴∠ACN=∠DCM,
在△ACN和△DCM中,
,
∴△ACN≌△DCM(AAS),
∴AN=DM,
∴S△BDC=S△AEC.
(3)如图4中,作DF∥BC交AB于F.延长CD交AB于H.
∵DF∥BE,DE∥BF,
∴四边形DEBF是平行四边形,
∴S△BDF=S△BDE,S△BDF=S△DFC,
∴S△DFC=S△BDE,
∵∠ABC=60°,BD平分∠ABC,
∴∠ABD=∠DBE=30°,
∵DF∥BE,
∴∠FDB=30°,
∴∠FBD=∠FDB=30°,
∴FB=FD,
∴四边形DEBF是菱形,
∵BD=CD=6,
∴∠DBC=∠DCB=30°,
∵∠DEC=∠ABC=60°,
∴∠CDE=90°,
∴DE=CD tan30°=6×=2,
∴BF=DE=2,
∵DE∥AB,
∴∠BHC=∠EDC=90°,
∴CH⊥AB,作点F关于CH的对称点F′,连接DF′,易知S△DFC=S△DF′C,
在Rt△DFH中,FH=HF′=DF sin30°=,
∴BF′=4,
综上所述,满足条件的BF的值为2或4.
10.∠OCE=∠OAC
11.(1)证明:
∵CB=CE,
∴∠CBE=∠CEB,
∵∠ABC=∠CED=90°,
∴∠DEF+∠CEB=90°,∠ABF+∠CBE=90°,
∴∠DEF=∠ABF.
(2)证明:如图①中,作AN⊥BF于N,DM⊥BF交BF的延长线于M.
∵∠ABN=∠DEM,∠ANB=∠M=90°,AB=DE,
∴△ANB≌△DME(AAS),
∴AN=DM,
∵∠ANF=∠M=90°,∠AFN=∠DFM,AN=DM,
∴△AFN≌△DFM(AAS),
∴AF=FD.
(3)解:如图②中,作AN⊥BF于N,DM⊥BF交BF的延长线于M.
在Rt△ABC中,∵∠ABC=90°,AC=5,BC=3,
∴AB==4,
∵EC⊥BC,
∴∠BCE=∠ACD=90°,
∵AC=CD=5,
∴AD=5,
∴DF=AF=AD=,
由旋转知,∠ACB=∠DCE,
∴∠ACD=∠ACE+DCE=∠ACB+∠ACE=90°,
∴∠MED=∠CEB=45°,
∴EM=MD=2,
在Rt△DFM中,FM==,
∴EF=EM-FM=.
12.AP=2PM
2
13.
14.(1)证明:∵AB=AC,AD=AE,
∴∠B=∠C,∠ADE=∠AED,
∵∠ADC=∠B+∠BAD=∠ADE+∠CDE,∠AED=∠C+∠CDE,
∴∠B+∠BAD=∠C+∠CDE+∠CDE,
∴∠BAD=2∠CDE.
(2)证明:如图2中,在FC上截取FM,使得FM=AF,连接DM
∵DF⊥AM,AF=FM,
∴DA=DM,
∴∠CAD=∠DMA,
∵∠CAD=2∠B=2∠C,∠AMD=∠C+∠MDC,
∴∠AMD=2∠C,
∴∠C=∠MDC,
∴MD=MC,
∴AD+AF=DM+FM=CM+FM=CF,
∴AC-CF=CF-CM,
∴AC-CF=CF-AD,
∴AC+AD=2CF.
(3)解:如图3中,在FC上截取FM,使得FM=AF,连接DM,CG.
设∠B=∠C=β,∠CDE=∠GDE=α,
∵∠CAD=2β,∠ADE=∠AED=α+β,
∴2β+2(α+β)=180°,
∴2β=90°-α,
∵∠AFD=90°,
∴∠ADF=∠MDF=α,
∴∠AEG=180°-α-β-(180°-2β)=2β,
∵AE=CM,
∴AM=CE=EG,
∵AD=AE,
∴△ADM≌△EAG(SAS),
∴AG=DM=AD=AE=8,
∵EC=2,
∴AC=AE+CE=10=AB,AF=FM=1,
∵DF2=AD2-AF2=CD2-CF2,
∴CD=12,
设BD=2m,则BC=2m+12,
作AH⊥BC于H,则CH=BH=m+6,
∴DH=6+m-2m=6-m,
∵AH2=AD2-DH2=2-CH2,
∴82-(6-m)2=102-(m+6)2,
解得m=,
∴BD=2m=3.
15.(-1,0)或(4,0)或(-11,0)
16.60°
AE=BD
17.证明:(1)由旋转的性质可得,∠DCE=90°,DC=EC,
∵∠ACB=∠DCE=90°,
∴∠ACD=∠BCE,
又∵AC=BC,DC=EC,
∴△ADC≌△BCE,
∴AD=BE;
(2)连结EF,
∵CD=EC,CF⊥DE,
∴CF平分DE,
∴CF垂直平分DE,
∴DF=EF,
∵∠ACB=90°,
∴∠ABC=∠A=∠CBE=45°,
∴∠FBE=90°,
∴BE2+BF2=EF2,
∴AD2+BF2=DF2;
(3)∵∠CDB=∠A+∠ACD=60°,∠CDE=45°,
∴∠EDB=15°,
∵DF=EF,
∴∠EDB=∠DEF=15°,
∴∠EFB=30°,
∴设BE为x,则EF=DF=2x,,
在等腰直角△CDE中,,
∴,
∵在Rt△BDE中,DE2=BD2+BE2,
∴ ,
解得,x=1,
∴.
18.解:(1)AC=BD,AC⊥BD,
理由如下:设AC与BO交于N,交BD于E,
∵∠AOB=∠COD=90°,
∴∠AOC=∠BOD,
在△AOC和△BOD中,
,
∴△AOC≌△BOD(SAS),
∴AC=BD,∠CAO=∠DBO,
又∵∠BNE=∠ANO,
∴∠BEN=∠AON=90°,
∴AC⊥BD;
(2)BC2+AC2=2OC2,
理由如下:如图2,连接BD,
∵∠AOB=∠COD=90°,OA=OB,OC=OD,
∴∠AOC=∠BOD,∠BAO=∠ABO=45°,CD=OC,
在△AOC和△BOD中,
,
∴△AOC≌△BOD(SAS),
∴AC=BD,∠CAO=∠DBO=45°,
∴∠CBD=90°,
∴BC2+BD2=CD2,
∴BC2+AC2=2OC2;
②如图3,当点C在BD上时,过点O作OH⊥CD于H,
∵OC=OD=5,∠COD=90°,
∴CD=5,
又∵OH⊥CD,
∴OH=CH=DH=,
∴BH===,
∴BD=BH+DH=+,
∵∠AOB=∠COD=90°,
∴∠AOC=∠BOD,
在△AOC和△BOD中,
,
∴△AOC≌△BOD(SAS),
∴AC=BD=+;
如图4,当点D在BC上时,过点O作OH⊥CD于H,
同理可求AC=BD=-;
综上所述:AC=+或-.
第2页,共31页
第1页,共31页
第二十三章旋转几何证明题提高篇1(含答案)
如图1,已知∠DAC=90°,△ABC是等边三角形,点P为射线AD上任意一点(点P与点A不重合),连结CP,将线段CP绕点C顺时针旋转60°得到线段CQ,连结QB并延长交直线AD于点E.
(1)如图1,猜想∠QEP=______°;
(2)如图2,3,若当∠DAC是锐角或钝角时,其它条件不变,猜想∠QEP的度数,选取一种情况加以证明;
(3)如图3,若∠DAC=135°,∠ACP=15°,且AC=4,求BQ的长.
如图1,在Rt△ABC中,∠A=90°,AB=AC,点D,E分别在边AB,AC上,AD=AE,连接DC,点M,P,N分别为DE,DC,BC的中点.
(1)观察猜想:
图1中,线段PM与PN的数量关系是______,位置关系是______;
(2)探究证明:
把△ADE绕点A逆时针方向旋转到图2的位置,连接MN,BD,CE,判断△PMN的形状,并说明理由;
(3)拓展延伸:
把△ADE绕点A在平面内自由旋转,若AD=4,AB=10,请直接写出△PMN面积的最大值.
问题背景:如图(1),在四边形ABCD中.若BC=CD,∠BAD=∠BCD=90°,则AC平分∠BAD.小明为了证明这个结论,将△ABC绕点C顺时针旋转90°,请帮助小明完成他的作图.
迁移应用:如图(2),在五边形ABCDE中,∠A=∠C=90°,AB=BC,AE+CD=DE,求证:BD平分∠CDE.
联系拓展:如图(3),在Rt△ABC中,AC=BC,若点D满足AD=AB,BD=AB,点P是AD的中点,直接写出的值.
如图,点A是线段BC上一点,ABD和ACE都是等边三角形.
(1)如图,连接BE,CD,求证:BE=CD.
(2)如图,将ABD绕点A顺时针旋转得到AB'D'.
当旋转角为 度时,边AD'落在边AE上.
在的条件下,延长DD'交CE于点P,连接BD',CD',当线段AB,AC满足什么数量关系时,BDD'与CPD'全等 并给予证明.
已知ABC中,AB=AC,D,E是BC边上的点,将ABD绕点A旋转,得到ACD',连接D'E.
(1)如图,当BAC=,DAE=时,求证:DE=D'E.
(2)如图,当DE=D'E时,DAE与BAC有怎样的数量关系,并说明理由.
(3)如图,在(2)的条件下,当BAC=,BD与DE满足怎样的数量关系时,D'EC是等腰直角三角形 (直接写出结论,不必说明理由)
如图1,菱形ABCD的顶点A,D在直线l上,∠BAD=60°,以点A为旋转中心将菱形ABCD顺时针旋转α(0°<α<30°),得到菱形AB′C′D′.B′C′交对角线AC于点M,C′D′交直线l于点N,连接MN.
(1)当MN∥B′D′时,求α的大小.
(2)如上图2,对角线B′D′交AC于点H,交直线l于点G,延长C′B′交AB于点E,连接EH.当△HEB′的周长为2时,求菱形ABCD的周长.
(1)探究发现:下面是一道例题及其解答过程,请补充完整:
如图,在等边三角形ABC内部,有一点P,若APB=.求证:+=.
证明:如图,将APC绕A点逆时针旋转得到AP'B,连接PP',则APP'为等边三角形.
APP'=,PA=PP',PC= .
又APB=,BPP'=.
+= ,即+=.
(2)类比延伸:如图,在等腰三角形ABC中,BAC=,内部有一点P,若APB=,试判断线段PA,PB,PC之间的数量关系,并证明.
(3)联想拓展:如图,在ABC中,BAC=,AB=AC,点P在直线AB的上方,且APB=,满足+=,请直接写出k的值.
已知:正方形ABCD中,∠MAN=45°,∠MAN绕点A顺时针旋转,它的两边分别交CB,DC(或它们的延长线)于点M,N.
(1)当∠MAN绕点A旋转到BM=DN时(如图1),易证MN=BM+DN.
(2)当∠MAN绕点A旋转到BM≠DN时(如图2),线段BM,DN和MN之间有怎样的数量关系?写出猜想,并加以证明.
(3)当∠MAN绕点A旋转到如图3的位置时,线段BM,DN和MN之间又有怎样的数量关系?写出猜想,并加以证明.
如图1,将两个完全相同的三角形纸片ABC和DEC重合放置,其中∠C=90°,∠B=∠E=30°.
(1)操作发现:
如图2,固定△ABC,使△DEC绕点C旋转,当点D恰好落在AB边上时,填空:
①线段DE与AC的位置关系是______;
②设△BDC的面积为S1,△AEC的面积为S2,则S1与S2的数量关系是______.
(2)猜想论证:
当△DEC绕点C旋转到如图3所示的位置时,小明猜想(1)中S1与S2的数量关系仍然成立,并尝试分别作出了△BDC和△AEC中BC、CE边上的高,请你证明小明的猜想.
(3)拓展探究
已知∠ABC=60°,点D是角平分线上一点,BD=CD=6,DE∥AB交BC于点E(如图4),若在射线BA上存在点F,使S△DCF=S△BDE,请求出相应的BF的长.
在Rt△ABC中,∠BCA=90°,∠A<∠ABC,D是AC边上一点,且DA=DB,O是AB的中点,CE是△BCD的中线.
(1)如图a,连接OC,请直接写出∠OCE和∠OAC的数量关系:______;
(2)点M是射线EC上的一个动点,将射线OM绕点O逆时针旋转得射线ON,使∠MON=∠ADB,ON与射线CA交于点N.
①如图b,猜想并证明线段OM和线段ON之间的数量关系;
②若∠BAC=30°,BC=m,当∠AON=15°时,请直接写出线段ME的长度(用含m的代数式表示).
如图①,在Rt△ABC中.∠ABC=90°.将△ABC绕点C顺时针旋转一定的角度得到△DEC.连接AD、BE.并延长BE交AD于点F.
(1)求证:∠DEF=∠ABF;
(2)求证:AF=DF;
(3)当EC⊥BC时,如图②,若AC=5,BC=3.求EF的长.
如图,点P是等边△ABC内一点,且∠BPC=120°,点M是边BC的中点,连接PA,PM.
(1)如图1,若点A,P,M三点共线,则AP与PM的数量关系是______
(2)如图2,若点A,P,M三点不共线,问(1)中的结论还成立吗?若成立,请给出证明,若不成立,请说明理由;
(3)如图3,若AB=2,=,直接写出AP的长是______.
如图1,在Rt△ABC中,∠B=90°,AB=4,BC=2,点D、E分别是边BC、AC的中点,连接DE.将△CDE绕点C逆时针方向旋转,记旋转角为α.
(1)问题发现
①当α=0°时,=______;②当α=180°时,=______.
(2)拓展探究
试判断:当0°≤α<360°时,的大小有无变化?请仅就图2的情形给出证明.
(3)问题解决
△CDE绕点C逆时针旋转至A、B、E三点在同一条直线上时,求线段BD的长.
如图1,△ABC中,AB=AC,点D在BC上,点E在AC上,且AE=AD.
(1)求证:∠BAD=2∠CDE;
(2)如图2,过点D作DF⊥AC,垂足为F,若∠CAD=2∠B,求证:AC+AD=2CF;
(3)如图3,在(2)的条件下,把△DCE沿DE翻折得到△DGE,若AG=8,CE=2,求BD的长.
平面直角坐标系中,点A(a,0)、B(0,b),且a、b满足:=-b2+6b-9,点A、C关于y轴对称,点F为x轴上一动点.
(1)求点A、B两点的坐标;
(2)如图1,若BC⊥CD,BA⊥EA,且BD=BE,连接ED交x轴于点M,求证:DM=ME;
(3)如图2,若BC⊥CD,且BC=CD,直线BC上存在某点G(m,3m+3),使△DFG为等腰直角三角形(点D、F,G按逆时针方向排列),请直接写出点F的坐标______.
如图,△ABC和△ECD都是等边三角形,直线AE,BD交于点F.
(1)如图1,当A,C,D三点在同一直线上时,∠AFB的度数为______
,线段AE与BD的数量关系为______
.
(2)如图2,当△ECD绕点C顺时针旋转α(0°≤α<360°)时,(1)中的结论是否还成立?若不成立,请说明理由;若成立,请就图2给予证明.
(3)若AC=4,CD=3,当△ECD绕点C顺时针旋转一周时,请直接写出BD长的取值范围.
在Rt△ACB中,∠ACB=90°,AC=BC,D为AB上一点,连接CD,将CD绕C点逆时针旋转90°至CE,连接DE,过C作CF⊥DE交AB于F,连接BE.
(1)求证:AD=BE;
(2)求线段AD、BF、DF之间的数量关系.
(3)若∠ACD=15°,CD=+1,求BF.
18.已知:∠AOB=∠COD=90°,OA=OB,OC=OD.(OC>OA)
(1)如图1:连AC、BD,判断:AC与BD之间的关系;并说明理由.
(2)若将△COD绕点O逆时针旋转,
①如图2,当点C恰好在AB边上时,请写出AC、BC、OC之间数量关系;并说明理由.
②当点B、D、C在同一条直线上时,若OB=6,OC=5,求AC的长.
1.解:(1)60;
(2)∠QEP=60°.以∠DAC是锐角为例.
证明:如图2,
∵△ABC是等边三角形,
∴AC=BC,∠ACB=60°,
∵线段CP绕点C顺时针旋转60°得到线段CQ,
∴CP=CQ,∠PCQ=6O°,
∴∠ACB+∠BCP=∠BCP+∠PCQ,
即∠ACP=∠BCQ,
在△ACP和△BCQ中,
,
∴△ACP≌△BCQ(SAS),
∴∠APC=∠Q,
∵∠1=∠2,
∴∠QEP=∠PCQ=60°;
(3) 作CH⊥AD于H,如图3,
与(2)一样可证明△ACP≌△BCQ,
∴AP=BQ,
∵∠DAC=135°,∠ACP=15°,
∴∠APC=30°,∠PCB=45°,
∴△ACH为等腰直角三角形,
∴AH=CH=AC=×4=2,
在Rt△PHC中,PH=CH=2,
∴PA=PH-AH=2-2,
∴BQ=2-2.
2.解:(1)PM=PN;PM⊥PN
(2) △PMN是等腰直角三角形.
由旋转知,∠BAD=∠CAE,
∵AB=AC,AD=AE,
∴△ABD≌△ACE(SAS),
∴∠ABD=∠ACE,BD=CE,
利用三角形的中位线得,PN=BD,PM=CE,
∴PM=PN,
∴△PMN是等腰三角形,
同(1)的方法得,PM∥CE,
∴∠DPM=∠DCE,
同(1)的方法得,PN∥BD,
∴∠PNC=∠DBC,
∵∠DPN=∠DCB+∠PNC=∠DCB+∠DBC,
∴∠MPN=∠DPM+∠DPN=∠DCE+∠DCB+∠DBC
=∠BCE+∠DBC=∠ACB+∠ACE+∠DBC
=∠ACB+∠ABD+∠DBC=∠ACB+∠ABC,
∵∠BAC=90°,
∴∠ACB+∠ABC=90°,
∴∠MPN=90°,
∴△PMN是等腰直角三角形;
(3)方法1:如图2,
同(2)的方法得,△PMN是等腰直角三角形,
∴MN最大时,△PMN的面积最大,
∴DE∥BC且DE在顶点A上面,
∴MN最大=AM+AN,
连接AM,AN,
在△ADE中,AD=AE=4,∠DAE=90°,
∴AM=2,
在Rt△ABC中,AB=AC=10,AN=5,
∴MN最大=2+5=7,
∴S△PMN最大=PM2=×MN2=×(7)2=.
方法2:由(2)知,△PMN是等腰直角三角形,PM=PN=BD,
∴PM最大时,△PMN面积最大,
∴点D在BA的延长线上,
∴BD=AB+AD=14,
∴PM=7,
∴S△PMN最大=PM2=×72=.
3.解:问题背景:
如图(1)所示,
作法:延长AD,在AD的延长线上取一点F使DF=AB,连接CF,
即:△CDF是△ABC绕点C顺时针旋转90°所得;
理由:在四边形ABCD中,∠BAD=∠BCD=90°,
∴∠BAD+∠BCD=180°,
∴∠ABC+∠ADC=180°,
∵∠ADC+∠CDF=180°,
∴∠ABC=∠CDF,
∵BC=CD,
∴△ABC≌△FDC(SAS),
∴∠BAC=∠DFC,AC=CF,
∴∠CAF=∠CFD,
∴∠BAC=∠DAC,
即:AC平分∠BAD;
迁移应用:如图(2),
连接BE,延长DC,在DC的延长线上取一点F,使CG=AE,连接BG,
∵∠A=∠BCD=90°,
∴∠BCG=90°=∠A,
∵BC=AB,
∴△BCG≌△BAE(SAS),
∴BG=BE,
∵AE+CD=DE,
∴CG+CD=DE,
即:DG=DE,
∵BD=BD,
∴△BDG≌△BDE(SSS),
∴∠BDG=∠BDE,
∴BD平分∠CDE;
联系拓展:当点D在AB上方时,如图(3),
连接CP,在PB的延长线上取一点Q,使BQ=AP,连接CQ,
设AB=13a,
∵AD=AB,BD=AB,
∴BD=13a,AD=10a,
∵点P是AD的中点,
∴BP=AP=AD=5a,
∵BD=AB,
∴BP⊥AD,
∴∠APD=90°,
∵∠ACB=90°,
∴∠APB+∠ACB=180°,
∴∠CBP+∠CAP=180°,
∵∠CBP+∠CBQ=180°,
∴∠CAP=∠CBQ,
∵AC=BC,
∴△ACP≌△BCQ(SAS),
∴CP=CQ,∠ACP=∠BCG,
∴∠PCQ=∠PCB+∠BCQ=∠PCB+∠ACP=∠ACB=90°,
在Rt△ABP中,根据勾股定理得,BP==12a,
∴PQ=BP+BQ=12a+5a=17a,
在Rt△PCQ中,PC=PQ=a,
∴==,
当点D在AB下方时,如图(4),
∵AB=BD,点P是AD的中点,
∴BP⊥AD,
∴AP=AD,∠BPA=90°=∠ACB,
∴∠CBP=∠CAP,
过点C作CH⊥CP交BP于H,
∴∠PCH=90°=∠ACB,
∴∠BCH=∠ACP,
∴△CBH≌△CAP(ASA),
∴BH=AP,
设AB=m,则AD=m,
∴AP=AD=m,
∴BH=m,
在Rt△APB时,BP==m,
∴PH=BP-BH=m,
∴CP==×m=,
∴==,
即:的值为或.
4.解:(1)证明:ACE,ABD都是等边三角形,
AB=AD,AE=AC,BAD=CAE=.
BAD+DAE=CAE+DAE,即BAE=DAC.
BAEDAC.
BE=CD.
(2)60
当AC=2AB时,BDD'与CPD'全等.
证明:由旋转和等边三角形的知识可知AB=BD=DD'=AD',
四边形ABDD'是菱形,
ABD'=DBD'=ABD=,DPBC.
ACE是等边三角形,
AC=AE=CE,ACE=.
AC=2AB,AE=2AD',
PCD'=ACD'=ACE=.
DPBC,
ABD'=DBD'=BD'D=ACD'=PCD'=PD'C=,
BD'=CD',
BDD'CPD'.
5.解:(1)证明:ABD绕点A旋转得到ACD',
AD=AD',CAD'=BAD.
BAC=,DAE=,
D'AE=CAD'+CAE=BAD+CAE=BAC-DAE=-=.
DAE=D'AE.
在ADE和AD'E中,
ADEAD'E(SAS).
DE=D'E.
(2)解:DAE=BAC.理由如下:
在ADE和AD'E中,
ADEAD'E(SSS).
DAE=D'AE.
BAD+CAE=CAD'+CAE=D'AE=DAE.
DAE=BAC.
(3)解:当DE=BD时,D'EC是等腰直角三角形.
6.解:(1)∵MN∥B′D′易证△C′MN是等边三角形
又∵C′B′=C′D′
∴MB′=ND′
在△AB′M和△AD′N中AB′=AD′,∠AB′M=∠AD′N,B′M=D′N
∴△AB′M △AD′N
∴∠B′AM=∠D′AN
又∵∠D′AN=α
∴∠B′AM=α
∴∠B′AM=∠BAB′=∠BAC=∠BAD=15°
即α=15°;
(2)在△AB′E和△AD′G中,
∠AB′E=∠AD′G,∠EAB′=∠GAD′,AB′=AD′
∴△AB′E △AD′G
∴EB′=GD′,
AE=AG在△AHE和△AHG中,
AE=AG,∠EAH=∠GAH,AH=AH
∴△AHE△AHG
∴EH=GH
∵△HEB′的周长为2
∴EH+EB′+B′H=2
∴GH+GD′+B′H=2
∴B′D′=BD=2
∴菱形ABCD的周长为8.
7.解:(1)BP';
(2)+=.
证明:如图,将APC绕A点逆时针旋转,得到AP'B,连接PP',
则P'A=PA,P'AP=,P'B=PC,
APP'=,=+=.
APB=,
BPP'=.
+=.
+=.
(3)k=±.
8.解:(1)如图1,连接AC,交MN于点G,
∵四边形ABCD为正方形,
∴BC=CD,且BM=DN,
∴CM=CN,且AC平分∠BCD,
∴AC⊥MN,且MG=GN,
∴∠MAG=∠NAG,
∵∠BAC=∠MAN=45°,即∠BAM+∠GAM=∠GAM+∠GAN,
∴∠BAM=∠GAN=∠GAM,
在△ABM和△AGM中,
∴△ABM≌△AGM(AAS),
∴BM=MG,同理可得GN=DN,
∴BM+DN=MG+GN=MN,
∴BM+DN=MN;
(2)猜想:BM+DN=MN,
证明如下:
如图2,在MB的延长线上,截取BE=DN,连接AE,
在△ABE和△ADN中,
∴△ABE≌△ADN(SAS),
∴AE=AN,∠EAB=∠NAD,
∵∠BAD=90°,∠MAN=45°,
∴∠BAM+∠DAN=45°,
∴∠EAB+∠BAM=45°,
∴∠EAM=∠NAM,
在△AEM和△ANM中
∴△AEM≌△ANM(SAS),
∴ME=MN,
又ME=BE+BM=BM+DN,
∴BM+DN=MN;
(3)DN-BM=MN.
证明如下:
如图3,在DC上截取DF=BM,连接AF,
△ABM和△ADF中,,
∴△ABM≌△ADF(SAS),
∴AM=AF,∠BAM=∠DAF,
∴∠BAM+∠BAF=∠BAF+∠DAF=90°,即∠MAF=∠BAD=90°,
∵∠MAN=45°,
∴∠MAN=∠FAN=45°,
在△MAN和△FAN中,
∴△MAN≌△FAN(SAS),
∴MN=NF,
∴MN=DN-DF=DN-BM,
∴DN-BM=MN.
9.(1)①DE∥AC,②S1=S2
;
(2)如图3中,
∵△DEC是由△ABC绕点C旋转得到,
∴BC=CE,AC=CD,
∵∠ACN+∠BCN=90°,∠DCM+∠BCN=180°-90°=90°,
∴∠ACN=∠DCM,
在△ACN和△DCM中,
,
∴△ACN≌△DCM(AAS),
∴AN=DM,
∴S△BDC=S△AEC.
(3)如图4中,作DF∥BC交AB于F.延长CD交AB于H.
∵DF∥BE,DE∥BF,
∴四边形DEBF是平行四边形,
∴S△BDF=S△BDE,S△BDF=S△DFC,
∴S△DFC=S△BDE,
∵∠ABC=60°,BD平分∠ABC,
∴∠ABD=∠DBE=30°,
∵DF∥BE,
∴∠FDB=30°,
∴∠FBD=∠FDB=30°,
∴FB=FD,
∴四边形DEBF是菱形,
∵BD=CD=6,
∴∠DBC=∠DCB=30°,
∵∠DEC=∠ABC=60°,
∴∠CDE=90°,
∴DE=CD tan30°=6×=2,
∴BF=DE=2,
∵DE∥AB,
∴∠BHC=∠EDC=90°,
∴CH⊥AB,作点F关于CH的对称点F′,连接DF′,易知S△DFC=S△DF′C,
在Rt△DFH中,FH=HF′=DF sin30°=,
∴BF′=4,
综上所述,满足条件的BF的值为2或4.
10.∠OCE=∠OAC
11.(1)证明:
∵CB=CE,
∴∠CBE=∠CEB,
∵∠ABC=∠CED=90°,
∴∠DEF+∠CEB=90°,∠ABF+∠CBE=90°,
∴∠DEF=∠ABF.
(2)证明:如图①中,作AN⊥BF于N,DM⊥BF交BF的延长线于M.
∵∠ABN=∠DEM,∠ANB=∠M=90°,AB=DE,
∴△ANB≌△DME(AAS),
∴AN=DM,
∵∠ANF=∠M=90°,∠AFN=∠DFM,AN=DM,
∴△AFN≌△DFM(AAS),
∴AF=FD.
(3)解:如图②中,作AN⊥BF于N,DM⊥BF交BF的延长线于M.
在Rt△ABC中,∵∠ABC=90°,AC=5,BC=3,
∴AB==4,
∵EC⊥BC,
∴∠BCE=∠ACD=90°,
∵AC=CD=5,
∴AD=5,
∴DF=AF=AD=,
由旋转知,∠ACB=∠DCE,
∴∠ACD=∠ACE+DCE=∠ACB+∠ACE=90°,
∴∠MED=∠CEB=45°,
∴EM=MD=2,
在Rt△DFM中,FM==,
∴EF=EM-FM=.
12.AP=2PM
2
13.
14.(1)证明:∵AB=AC,AD=AE,
∴∠B=∠C,∠ADE=∠AED,
∵∠ADC=∠B+∠BAD=∠ADE+∠CDE,∠AED=∠C+∠CDE,
∴∠B+∠BAD=∠C+∠CDE+∠CDE,
∴∠BAD=2∠CDE.
(2)证明:如图2中,在FC上截取FM,使得FM=AF,连接DM
∵DF⊥AM,AF=FM,
∴DA=DM,
∴∠CAD=∠DMA,
∵∠CAD=2∠B=2∠C,∠AMD=∠C+∠MDC,
∴∠AMD=2∠C,
∴∠C=∠MDC,
∴MD=MC,
∴AD+AF=DM+FM=CM+FM=CF,
∴AC-CF=CF-CM,
∴AC-CF=CF-AD,
∴AC+AD=2CF.
(3)解:如图3中,在FC上截取FM,使得FM=AF,连接DM,CG.
设∠B=∠C=β,∠CDE=∠GDE=α,
∵∠CAD=2β,∠ADE=∠AED=α+β,
∴2β+2(α+β)=180°,
∴2β=90°-α,
∵∠AFD=90°,
∴∠ADF=∠MDF=α,
∴∠AEG=180°-α-β-(180°-2β)=2β,
∵AE=CM,
∴AM=CE=EG,
∵AD=AE,
∴△ADM≌△EAG(SAS),
∴AG=DM=AD=AE=8,
∵EC=2,
∴AC=AE+CE=10=AB,AF=FM=1,
∵DF2=AD2-AF2=CD2-CF2,
∴CD=12,
设BD=2m,则BC=2m+12,
作AH⊥BC于H,则CH=BH=m+6,
∴DH=6+m-2m=6-m,
∵AH2=AD2-DH2=2-CH2,
∴82-(6-m)2=102-(m+6)2,
解得m=,
∴BD=2m=3.
15.(-1,0)或(4,0)或(-11,0)
16.60°
AE=BD
17.证明:(1)由旋转的性质可得,∠DCE=90°,DC=EC,
∵∠ACB=∠DCE=90°,
∴∠ACD=∠BCE,
又∵AC=BC,DC=EC,
∴△ADC≌△BCE,
∴AD=BE;
(2)连结EF,
∵CD=EC,CF⊥DE,
∴CF平分DE,
∴CF垂直平分DE,
∴DF=EF,
∵∠ACB=90°,
∴∠ABC=∠A=∠CBE=45°,
∴∠FBE=90°,
∴BE2+BF2=EF2,
∴AD2+BF2=DF2;
(3)∵∠CDB=∠A+∠ACD=60°,∠CDE=45°,
∴∠EDB=15°,
∵DF=EF,
∴∠EDB=∠DEF=15°,
∴∠EFB=30°,
∴设BE为x,则EF=DF=2x,,
在等腰直角△CDE中,,
∴,
∵在Rt△BDE中,DE2=BD2+BE2,
∴ ,
解得,x=1,
∴.
18.解:(1)AC=BD,AC⊥BD,
理由如下:设AC与BO交于N,交BD于E,
∵∠AOB=∠COD=90°,
∴∠AOC=∠BOD,
在△AOC和△BOD中,
,
∴△AOC≌△BOD(SAS),
∴AC=BD,∠CAO=∠DBO,
又∵∠BNE=∠ANO,
∴∠BEN=∠AON=90°,
∴AC⊥BD;
(2)BC2+AC2=2OC2,
理由如下:如图2,连接BD,
∵∠AOB=∠COD=90°,OA=OB,OC=OD,
∴∠AOC=∠BOD,∠BAO=∠ABO=45°,CD=OC,
在△AOC和△BOD中,
,
∴△AOC≌△BOD(SAS),
∴AC=BD,∠CAO=∠DBO=45°,
∴∠CBD=90°,
∴BC2+BD2=CD2,
∴BC2+AC2=2OC2;
②如图3,当点C在BD上时,过点O作OH⊥CD于H,
∵OC=OD=5,∠COD=90°,
∴CD=5,
又∵OH⊥CD,
∴OH=CH=DH=,
∴BH===,
∴BD=BH+DH=+,
∵∠AOB=∠COD=90°,
∴∠AOC=∠BOD,
在△AOC和△BOD中,
,
∴△AOC≌△BOD(SAS),
∴AC=BD=+;
如图4,当点D在BC上时,过点O作OH⊥CD于H,
同理可求AC=BD=-;
综上所述:AC=+或-.
第2页,共31页
第1页,共31页
同课章节目录
