2021-2022学年人教版八年级数学上册11.2.2 三角形的外角 课后作业 (word版含答案)
文档属性
| 名称 | 2021-2022学年人教版八年级数学上册11.2.2 三角形的外角 课后作业 (word版含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 81.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-05 10:43:34 | ||
图片预览


文档简介
第十一章
三角形
11.2.2 三角形的外角
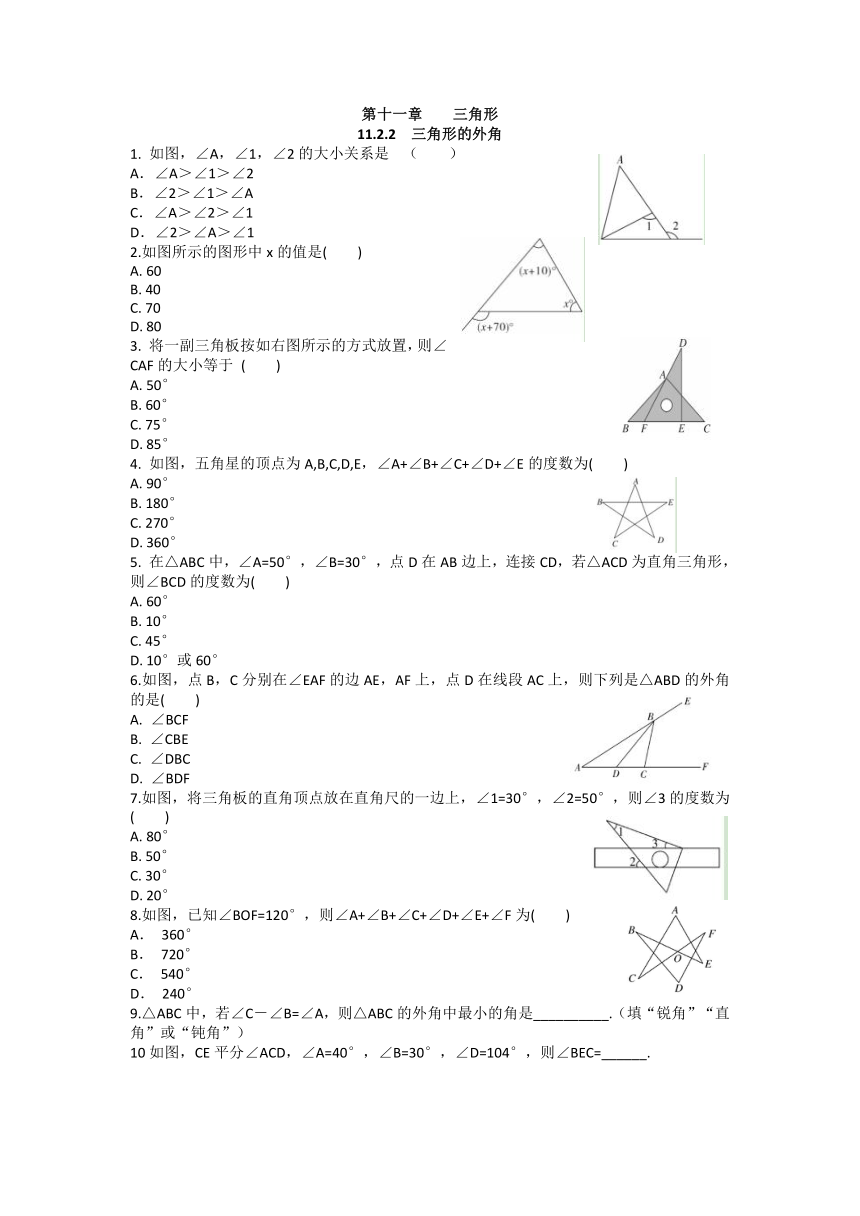
1.
如图,∠A,∠1,∠2的大小关系是
( )
A.∠A>∠1>∠2
B.∠2>∠1>∠A
C.∠A>∠2>∠1
D.∠2>∠A>∠1
2.如图所示的图形中x的值是( )
A.
60
B.
40
C.
70
D.
80
3.
将一副三角板按如右图所示的方式放置,则∠CAF的大小等于
( )
A.
50°
B.
60°
C.
75°
D.
85°
4.
如图,五角星的顶点为A,B,C,D,E,∠A+∠B+∠C+∠D+∠E的度数为( )
A.
90°
B.
180°
C.
270°
D.
360°
5.
在△ABC中,∠A=50°,∠B=30°,点D在AB边上,连接CD,若△ACD为直角三角形,则∠BCD的度数为( )
A.
60°
B.
10°
C.
45°
D.
10°或60°
6.如图,点B,C分别在∠EAF的边AE,AF上,点D在线段AC上,则下列是△ABD的外角的是( )
A.
∠BCF
B.
∠CBE
C.
∠DBC
D.
∠BDF
7.如图,将三角板的直角顶点放在直角尺的一边上,∠1=30°,∠2=50°,则∠3的度数为( )
A.
80°
B.
50°
C.
30°
D.
20°
8.如图,已知∠BOF=120°,则∠A+∠B+∠C+∠D+∠E+∠F为( )
A.
360°
B.
720°
C.
540°
D.
240°
9.△ABC中,若∠C-∠B=∠A,则△ABC的外角中最小的角是__________.(填“锐角”“直角”或“钝角”)
10如图,CE平分∠ACD,∠A=40°,∠B=30°,∠D=104°,则∠BEC=______.
11.
如图,在△ABC中,∠ABC=∠ACB,AD,BD,CD分别平分△ABC的外角∠EAC,内角∠ABC,外角∠ACF.有下列结论:①AD∥BC;②∠ACB=∠ADB;③∠ADC+∠ABD=90°;④∠ADB=45°-12∠CDB.其中正确的结论有_________.(填序号)
12.如图,已知D为BC上一点,∠B=∠1,∠BAC=74°,求∠2的度数.
13.如图,∠ABC的平分线与△ABC的外角的平分线相交于点E.
(1)已知∠A=60°,求∠E的度数;
(2)写出∠A与∠E的数量关系:___________.
如图,∠A=50°,∠ABD=35°,∠ACB=70°,且CE平分∠ACB,求∠BEC的度数.
15.如图,已知在△ABC中,CE是外角∠ACD的平分线,BE是∠ABC的平分线.
(1)求证:∠A=2∠E;
(2)若∠A=∠ABC,求证:AB∥CE.
参考答案
1——8
BACBDDDD
直角
57°
①③④
解:∵∠B=∠1,∠BAC=74°,
∴∠B+∠BAD=∠BAC=74°.
∵∠2是△ABD的外角,
∴∠2=∠B+∠BAD=74°.
13.
(1)解:∵CE,BE分别平分∠ACD,∠ABC,
∴∠ECD=∠ACD,
∠EBC=∠ABC.
∴∠E=∠ECD-∠EBD=(∠ACD-∠ABC)=∠A=30°.
(2)∠A=2∠E
14.
解:在△ABC中,∵∠A=50°,∠ACB=70°,
∴∠ABC=60°.
∵∠ABD=35°,∴∠CBD=∠ABC-∠ABD=25°.
∵CE平分∠ACB,∴∠BCE=∠ACB=35°.
∴在△BCE中,∠BEC=180°-25°-35°=120°.
15.
证明:(1)∵∠ACD是△ABC的一个外角,∠2是△BCE的一个外角,
∴∠ACD=∠ABC+∠A,∠2=∠1+∠E.
∴∠A=∠ACD-∠ABC,∠E=∠2-∠1.
∵CE是外角∠ACD的平分线,BE是∠ABC的平分线,
∴∠ACD=2∠2,∠ABC=2∠1.
∴∠A=2∠2-2∠1=2(∠2-∠1)=2∠E.
(2)由(1)可知∠A=2∠E.
∵∠A=∠ABC,∠ABC=2∠4,
∴2∠E=2∠4,即∠E=∠4.
∴AB∥CE.
三角形
11.2.2 三角形的外角
1.
如图,∠A,∠1,∠2的大小关系是
( )
A.∠A>∠1>∠2
B.∠2>∠1>∠A
C.∠A>∠2>∠1
D.∠2>∠A>∠1
2.如图所示的图形中x的值是( )
A.
60
B.
40
C.
70
D.
80
3.
将一副三角板按如右图所示的方式放置,则∠CAF的大小等于
( )
A.
50°
B.
60°
C.
75°
D.
85°
4.
如图,五角星的顶点为A,B,C,D,E,∠A+∠B+∠C+∠D+∠E的度数为( )
A.
90°
B.
180°
C.
270°
D.
360°
5.
在△ABC中,∠A=50°,∠B=30°,点D在AB边上,连接CD,若△ACD为直角三角形,则∠BCD的度数为( )
A.
60°
B.
10°
C.
45°
D.
10°或60°
6.如图,点B,C分别在∠EAF的边AE,AF上,点D在线段AC上,则下列是△ABD的外角的是( )
A.
∠BCF
B.
∠CBE
C.
∠DBC
D.
∠BDF
7.如图,将三角板的直角顶点放在直角尺的一边上,∠1=30°,∠2=50°,则∠3的度数为( )
A.
80°
B.
50°
C.
30°
D.
20°
8.如图,已知∠BOF=120°,则∠A+∠B+∠C+∠D+∠E+∠F为( )
A.
360°
B.
720°
C.
540°
D.
240°
9.△ABC中,若∠C-∠B=∠A,则△ABC的外角中最小的角是__________.(填“锐角”“直角”或“钝角”)
10如图,CE平分∠ACD,∠A=40°,∠B=30°,∠D=104°,则∠BEC=______.
11.
如图,在△ABC中,∠ABC=∠ACB,AD,BD,CD分别平分△ABC的外角∠EAC,内角∠ABC,外角∠ACF.有下列结论:①AD∥BC;②∠ACB=∠ADB;③∠ADC+∠ABD=90°;④∠ADB=45°-12∠CDB.其中正确的结论有_________.(填序号)
12.如图,已知D为BC上一点,∠B=∠1,∠BAC=74°,求∠2的度数.
13.如图,∠ABC的平分线与△ABC的外角的平分线相交于点E.
(1)已知∠A=60°,求∠E的度数;
(2)写出∠A与∠E的数量关系:___________.
如图,∠A=50°,∠ABD=35°,∠ACB=70°,且CE平分∠ACB,求∠BEC的度数.
15.如图,已知在△ABC中,CE是外角∠ACD的平分线,BE是∠ABC的平分线.
(1)求证:∠A=2∠E;
(2)若∠A=∠ABC,求证:AB∥CE.
参考答案
1——8
BACBDDDD
直角
57°
①③④
解:∵∠B=∠1,∠BAC=74°,
∴∠B+∠BAD=∠BAC=74°.
∵∠2是△ABD的外角,
∴∠2=∠B+∠BAD=74°.
13.
(1)解:∵CE,BE分别平分∠ACD,∠ABC,
∴∠ECD=∠ACD,
∠EBC=∠ABC.
∴∠E=∠ECD-∠EBD=(∠ACD-∠ABC)=∠A=30°.
(2)∠A=2∠E
14.
解:在△ABC中,∵∠A=50°,∠ACB=70°,
∴∠ABC=60°.
∵∠ABD=35°,∴∠CBD=∠ABC-∠ABD=25°.
∵CE平分∠ACB,∴∠BCE=∠ACB=35°.
∴在△BCE中,∠BEC=180°-25°-35°=120°.
15.
证明:(1)∵∠ACD是△ABC的一个外角,∠2是△BCE的一个外角,
∴∠ACD=∠ABC+∠A,∠2=∠1+∠E.
∴∠A=∠ACD-∠ABC,∠E=∠2-∠1.
∵CE是外角∠ACD的平分线,BE是∠ABC的平分线,
∴∠ACD=2∠2,∠ABC=2∠1.
∴∠A=2∠2-2∠1=2(∠2-∠1)=2∠E.
(2)由(1)可知∠A=2∠E.
∵∠A=∠ABC,∠ABC=2∠4,
∴2∠E=2∠4,即∠E=∠4.
∴AB∥CE.
