山东省菏泽市鄄城县2020-2021学年七年级下学期期末数学试卷(Word版 含解析)
文档属性
| 名称 | 山东省菏泽市鄄城县2020-2021学年七年级下学期期末数学试卷(Word版 含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 333.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-05 10:27:14 | ||
图片预览


文档简介
2020-2021学年山东省菏泽市鄄城县七年级(下)期末数学试卷
一、选择题(每题3分,共24分)
1.(3分)下列交通标志图案是轴对称图形的是( )
A.
B.
C.
D.
2.(3分)下列说法中不正确的是( )
A.“某射击运动员射击一次,正中靶心”属于随机事件
B.“13名同学至少有两名同学的出生月份相同”属于必然事件
C.“在标准大气压下,当温度降到﹣1℃时,水结成冰”属于随机事件
D.“某袋中只有5个球,且都是黄球,任意摸出一球是白球”属于不可能事件
3.(3分)下列计算错误的有( )
①(2x+y)2=4x2+y2
②(3b﹣a)2=9b2﹣a2
③(﹣3b﹣a)(a﹣3b)=a2﹣9b2
④(﹣x﹣y)2=x2﹣2xy+y2
⑤(x﹣)2=x2﹣x+.
A.1个
B.2个
C.3个
D.4个
4.(3分)如图是一个风筝的图案,它是以直线AF为对称轴的轴对称图形,下列结论中不一定成立的是( )
A.△ABD≌△ACD
B.AF垂直平分EG
C.直线BG,CE的交点在AF上
D.△DEG是等边三角形
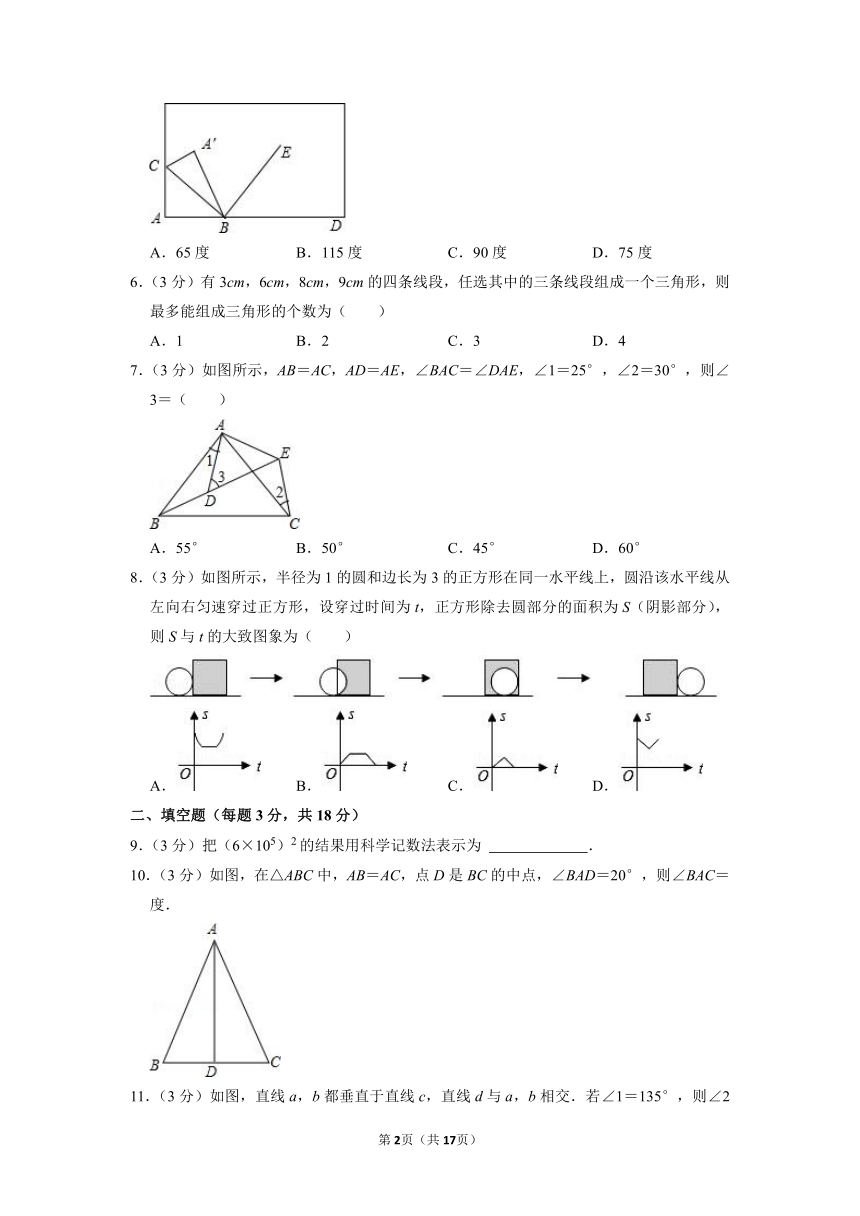
5.(3分)如图,将长方形纸片的一角折叠,使顶点A落在点A′处,BC为折痕,若BE是∠A′BD的平分线,则∠CBE的度数是( )
A.65度
B.115度
C.90度
D.75度
6.(3分)有3cm,6cm,8cm,9cm的四条线段,任选其中的三条线段组成一个三角形,则最多能组成三角形的个数为( )
A.1
B.2
C.3
D.4
7.(3分)如图所示,AB=AC,AD=AE,∠BAC=∠DAE,∠1=25°,∠2=30°,则∠3=( )
A.55°
B.50°
C.45°
D.60°
8.(3分)如图所示,半径为1的圆和边长为3的正方形在同一水平线上,圆沿该水平线从左向右匀速穿过正方形,设穿过时间为t,正方形除去圆部分的面积为S(阴影部分),则S与t的大致图象为( )
A.
B.
C.
D.
二、填空题(每题3分,共18分)
9.(3分)把(6×105)2的结果用科学记数法表示为
.
10.(3分)如图,在△ABC中,AB=AC,点D是BC的中点,∠BAD=20°,则∠BAC=
度.
11.(3分)如图,直线a,b都垂直于直线c,直线d与a,b相交.若∠1=135°,则∠2=
°.
12.(3分)某校学生会提倡双休日到养老院参加服务活动,首次活动需要7位同学参加,现有包括小杰在内的50位同学报名,因此学生会将从这50位同学中随机抽取7位,小杰被抽到参加首次活动的概率是
.
13.(3分)若
(x+3)(x﹣4)=ax2+bx+c,则a=
、b=
、c=
.
14.(3分)如图,将一副三角板和一张对边平行的纸条按如图方式摆放,两个三角板的一直角边重合,含30°角的直角三角板的斜边与纸条一边重合,含45°角的三角板的一个顶点在纸条的另一边上,则∠1的度数是
.
三、解答题(共78分)
15.(6分)计算或化简:
(1)|﹣3|+(﹣1)2017×(π﹣3)0﹣()﹣3;
(2)(2a3b2﹣4a4b3+6a5b4)+(﹣2a3b2).
16.(6分)先化简,再求值:(3x+2y)2﹣(3x﹣2y)2+2(x+y)(x﹣y)﹣2(x+4y),其中x=1,y=﹣1.
17.(6分)如图,AD、BC相交于点O,OA=OC,∠OBD=∠ODB.求证:AB=CD.
18.(8分)如图,已知AB∥CD,DA平分∠BDC,∠A=∠C.
(1)试说明:CE∥AD;
(2)若∠C=30°,求∠B的度数.
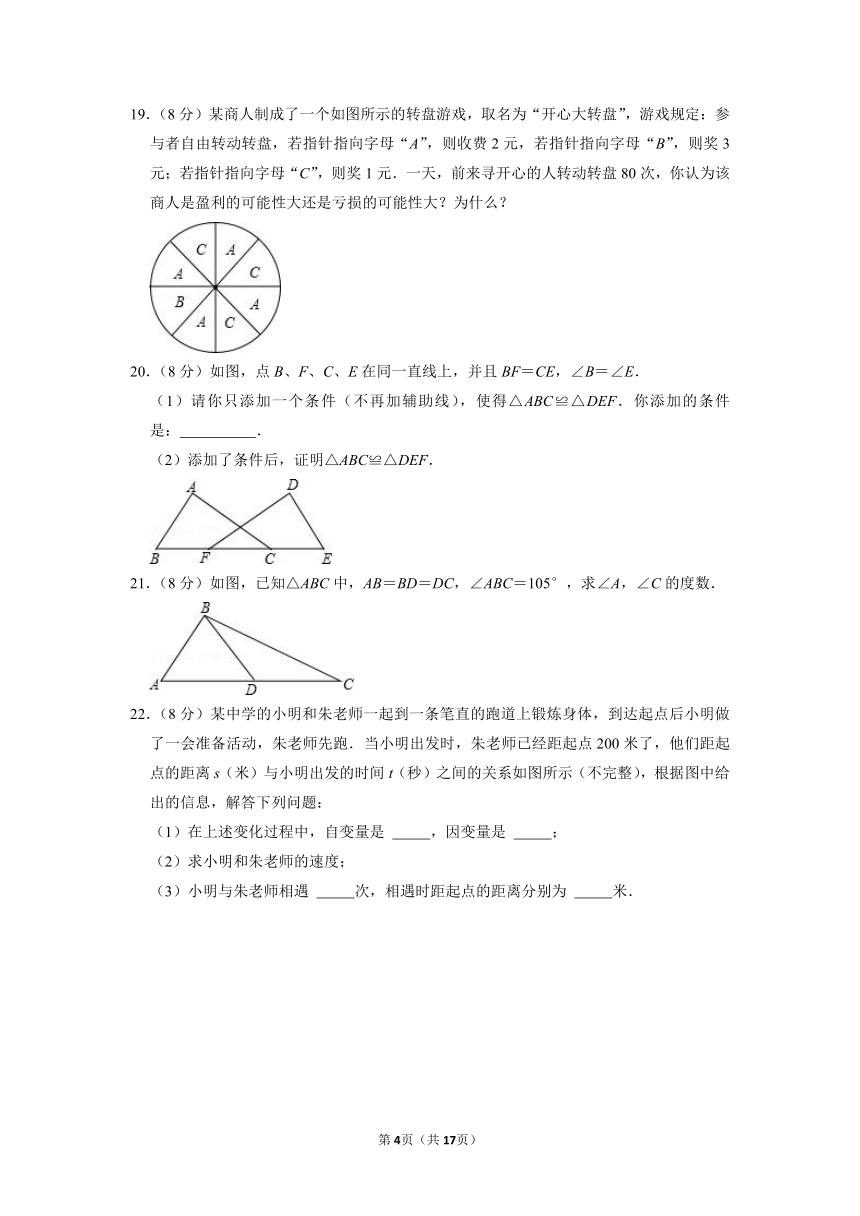
19.(8分)某商人制成了一个如图所示的转盘游戏,取名为“开心大转盘”,游戏规定:参与者自由转动转盘,若指针指向字母“A”,则收费2元,若指针指向字母“B”,则奖3元;若指针指向字母“C”,则奖1元.一天,前来寻开心的人转动转盘80次,你认为该商人是盈利的可能性大还是亏损的可能性大?为什么?
20.(8分)如图,点B、F、C、E在同一直线上,并且BF=CE,∠B=∠E.
(1)请你只添加一个条件(不再加辅助线),使得△ABC≌△DEF.你添加的条件是:
.
(2)添加了条件后,证明△ABC≌△DEF.
21.(8分)如图,已知△ABC中,AB=BD=DC,∠ABC=105°,求∠A,∠C的度数.
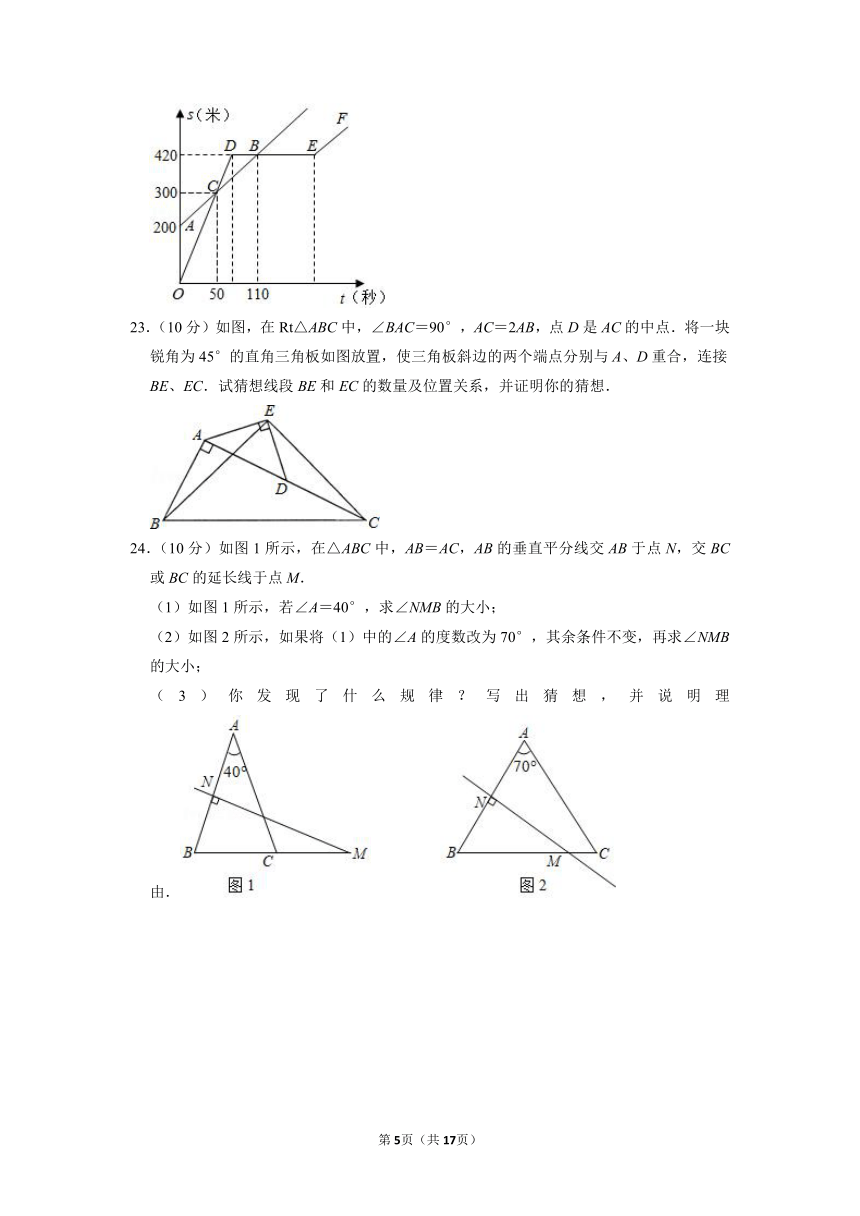
22.(8分)某中学的小明和朱老师一起到一条笔直的跑道上锻炼身体,到达起点后小明做了一会准备活动,朱老师先跑.当小明出发时,朱老师已经距起点200米了,他们距起点的距离s(米)与小明出发的时间t(秒)之间的关系如图所示(不完整),根据图中给出的信息,解答下列问题:
(1)在上述变化过程中,自变量是
,因变量是
;
(2)求小明和朱老师的速度;
(3)小明与朱老师相遇
次,相遇时距起点的距离分别为
米.
23.(10分)如图,在Rt△ABC中,∠BAC=90°,AC=2AB,点D是AC的中点.将一块锐角为45°的直角三角板如图放置,使三角板斜边的两个端点分别与A、D重合,连接BE、EC.试猜想线段BE和EC的数量及位置关系,并证明你的猜想.
24.(10分)如图1所示,在△ABC中,AB=AC,AB的垂直平分线交AB于点N,交BC或BC的延长线于点M.
(1)如图1所示,若∠A=40°,求∠NMB的大小;
(2)如图2所示,如果将(1)中的∠A的度数改为70°,其余条件不变,再求∠NMB的大小;
(3)你发现了什么规律?写出猜想,并说明理由.
2020-2021学年山东省菏泽市鄄城县七年级(下)期末数学试卷
参考答案与试题解析
一、选择题(每题3分,共24分)
1.(3分)下列交通标志图案是轴对称图形的是( )
A.
B.
C.
D.
【解答】解:A、不是轴对称图形,故本选项错误;
B、是轴对称图形,故本选项正确;
C、不是轴对称图形,故本选项错误;
D、不是轴对称图形,故本选项错误;
故选:B.
2.(3分)下列说法中不正确的是( )
A.“某射击运动员射击一次,正中靶心”属于随机事件
B.“13名同学至少有两名同学的出生月份相同”属于必然事件
C.“在标准大气压下,当温度降到﹣1℃时,水结成冰”属于随机事件
D.“某袋中只有5个球,且都是黄球,任意摸出一球是白球”属于不可能事件
【解答】解:A、“某射击运动员射击一次,正中靶心”属于随机事件,正确;
B、“13名同学至少有两名同学的出生月份相同”属于必然事件,正确;
C、在标准大气压下,当温度降到﹣1℃时,水结成冰”属于必然事件;
D、“某袋中只有5个球,且都是黄球,任意摸出一球是白球”属于不可能事件,正确.
故选:C.
3.(3分)下列计算错误的有( )
①(2x+y)2=4x2+y2
②(3b﹣a)2=9b2﹣a2
③(﹣3b﹣a)(a﹣3b)=a2﹣9b2
④(﹣x﹣y)2=x2﹣2xy+y2
⑤(x﹣)2=x2﹣x+.
A.1个
B.2个
C.3个
D.4个
【解答】解:①(2x+y)2=4x2+4xy+y2,本选项错误;
②(3b﹣a)2=9b2﹣6ab+a2,本选项错误;
③(﹣3b﹣a)(a﹣3b)=9b2﹣a2,本选项错误;
④(﹣x﹣y)2=(x+y)2=x2+2xy+y2,本选项错误;
⑤(x﹣)2=x2﹣x+,本选项正确,
则错误的个数为4个.
故选:D.
4.(3分)如图是一个风筝的图案,它是以直线AF为对称轴的轴对称图形,下列结论中不一定成立的是( )
A.△ABD≌△ACD
B.AF垂直平分EG
C.直线BG,CE的交点在AF上
D.△DEG是等边三角形
【解答】解:A、因为此图形是轴对称图形,正确;
B、对称轴垂直平分对应点连线,正确;
C、由三角形全等可知,BG=CE,且直线BG,CE的交点在AF上,正确;
D、题目中没有60°条件,不能判断是等边三角形,错误.
故选:D.
5.(3分)如图,将长方形纸片的一角折叠,使顶点A落在点A′处,BC为折痕,若BE是∠A′BD的平分线,则∠CBE的度数是( )
A.65度
B.115度
C.90度
D.75度
【解答】解:由折叠的性质,∠ABC=∠A′BC,
∵BE是∠A′BD的平分线,
∴∠EBA′=∠EBD,
∴∠CBE=2(∠A′BC+∠EBA′)÷2=180°÷2=90°
故选:C.
6.(3分)有3cm,6cm,8cm,9cm的四条线段,任选其中的三条线段组成一个三角形,则最多能组成三角形的个数为( )
A.1
B.2
C.3
D.4
【解答】解:四条木棒的所有组合:3,6,8和3,6,9和6,8,9和3,8,9;
只有3,6,8和6,8,9;3,8,9能组成三角形.
故选:C.
7.(3分)如图所示,AB=AC,AD=AE,∠BAC=∠DAE,∠1=25°,∠2=30°,则∠3=( )
A.55°
B.50°
C.45°
D.60°
【解答】解:∵∠BAC=∠DAE,
∴∠BAC﹣∠DAC=∠DAE﹣∠DAC,
∴∠1=∠EAC,
在△BAD和△EAC中,,
∴△BAD≌△EAC(SAS),
∴∠2=∠ABD=30°,
∵∠1=25°,
∴∠3=∠1+∠ABD=25°+30°=55°,
故选:A.
8.(3分)如图所示,半径为1的圆和边长为3的正方形在同一水平线上,圆沿该水平线从左向右匀速穿过正方形,设穿过时间为t,正方形除去圆部分的面积为S(阴影部分),则S与t的大致图象为( )
A.
B.
C.
D.
【解答】解:由图中可知:在开始的时候,阴影部分的面积最大,可以排除B,C.
随着圆的穿行开始,阴影部分的面积开始减小,当圆完全进入正方形时,阴影部分的面积开始不再变化.应排除D.
故选:A.
二、填空题(每题3分,共18分)
9.(3分)把(6×105)2的结果用科学记数法表示为
3.6×1011 .
【解答】解:(6×105)2
=62×(105)2
=36×1010
=3.6×1011.
故答案为:3.6×1011.
10.(3分)如图,在△ABC中,AB=AC,点D是BC的中点,∠BAD=20°,则∠BAC= 40 度.
【解答】解:∵AB=CA,
∴△ABC是等腰三角形,
∵D是BC边上的中点,
∴AD平分∠BAC,
∵∠BAD=20°.
∴∠BAC=2×20°=40°.
故答案为:40.
11.(3分)如图,直线a,b都垂直于直线c,直线d与a,b相交.若∠1=135°,则∠2= 45 °.
【解答】解:如图,
∵a⊥c、b⊥c,
∴a∥b,
∵∠1=∠3=135°,
∴∠2+∠3=180°,
则∠3=45°,
故答案为:45.
12.(3分)某校学生会提倡双休日到养老院参加服务活动,首次活动需要7位同学参加,现有包括小杰在内的50位同学报名,因此学生会将从这50位同学中随机抽取7位,小杰被抽到参加首次活动的概率是 .
【解答】解:∵学生会将从这50位同学中随机抽取7位,
∴小杰被抽到参加首次活动的概率是:.
故答案为:.
13.(3分)若
(x+3)(x﹣4)=ax2+bx+c,则a= 1 、b= ﹣1 、c= ﹣12 .
【解答】解:∵(x+3)(x﹣4)=x2﹣x﹣12,
(x+3)(x﹣4)=ax2+bx+c,
∴ax2+bx+c=x2﹣x﹣12,
∴a=1,b=﹣1,c=﹣12.
故答案为1,﹣1,﹣12.
14.(3分)如图,将一副三角板和一张对边平行的纸条按如图方式摆放,两个三角板的一直角边重合,含30°角的直角三角板的斜边与纸条一边重合,含45°角的三角板的一个顶点在纸条的另一边上,则∠1的度数是
15° .
【解答】解:如图,过A点作AB∥a,
∴∠1=∠2,
∵a∥b,
∴AB∥b,
∴∠3=∠4=30°,
而∠2+∠3=45°,
∴∠2=15°,
∴∠1=15°.
故答案为15°.
三、解答题(共78分)
15.(6分)计算或化简:
(1)|﹣3|+(﹣1)2017×(π﹣3)0﹣()﹣3;
(2)(2a3b2﹣4a4b3+6a5b4)+(﹣2a3b2).
【解答】解(1)|﹣3|+(﹣1)2017×(π﹣3)0﹣()﹣3
=3+(﹣1)×1﹣(﹣8)
=3﹣1+8
=10.
(2)(2a3b2﹣4a4b3+6a5b4)+(﹣2a3b2)
=2a3b2﹣4a4b3+6a5b4﹣2a3b2
=(2a3b2﹣2a3b2)+(﹣4a4b3+6a5b4)
=0+(﹣4a4b3+6a5b4)
=﹣4a4b3+6a5b4.
16.(6分)先化简,再求值:(3x+2y)2﹣(3x﹣2y)2+2(x+y)(x﹣y)﹣2(x+4y),其中x=1,y=﹣1.
【解答】解:(3x+2y)2﹣(3x﹣2y)2+2(x+y)(x﹣y)﹣2(x+4y)
=9x2+12xy+4y2﹣9x2+12xy﹣4y2+2x2﹣2y2﹣2x﹣8y
=2x2+24xy﹣2y2﹣2x﹣8y,
当x=1,y=﹣1时,原式=2×12+24×1×(﹣1)﹣2×(﹣1)2﹣2×1﹣8×(﹣1)=﹣18.
17.(6分)如图,AD、BC相交于点O,OA=OC,∠OBD=∠ODB.求证:AB=CD.
【解答】证明:∵∠OBD=∠ODB.
∴OB=OD,
在△AOB与△COD中,
∴△AOB≌△COD(SAS)
∴AB=CD.
18.(8分)如图,已知AB∥CD,DA平分∠BDC,∠A=∠C.
(1)试说明:CE∥AD;
(2)若∠C=30°,求∠B的度数.
【解答】解:(1)∵AB∥CD,
∴∠A=∠ADC.
∵∠A=∠C,
∴∠ADC=∠C,
∴CE∥AD;
(2)由(1)可得∠ADC=∠C=30°.
∵DA平分∠BDC,∠ADC=∠ADB,
∴∠CDB=2∠ADC=60°.
∵AB∥DC,
∴∠B+∠CDB=180°,
∴∠B=180°﹣∠CDB=120°.
19.(8分)某商人制成了一个如图所示的转盘游戏,取名为“开心大转盘”,游戏规定:参与者自由转动转盘,若指针指向字母“A”,则收费2元,若指针指向字母“B”,则奖3元;若指针指向字母“C”,则奖1元.一天,前来寻开心的人转动转盘80次,你认为该商人是盈利的可能性大还是亏损的可能性大?为什么?
【解答】解:商人盈利的可能性大
PA=80×=40(次);
PB=80×=10(次);
PC=80×=30(次);
理由:商人盈利:(元)
商人亏损:=60(元)
因为80>60
所以商人盈利的可能性大.
20.(8分)如图,点B、F、C、E在同一直线上,并且BF=CE,∠B=∠E.
(1)请你只添加一个条件(不再加辅助线),使得△ABC≌△DEF.你添加的条件是: ∠A=∠D .
(2)添加了条件后,证明△ABC≌△DEF.
【解答】解:(1)故答案为:∠A=∠D.
(2)证明:∵BF=CE,
∴BF+FC=EC+FC,
∴在△ABC和△DEF中,
,
∴△ABC≌△DEF(AAS)
21.(8分)如图,已知△ABC中,AB=BD=DC,∠ABC=105°,求∠A,∠C的度数.
【解答】解:∵AB=BD,
∴∠BDA=∠A,
∵BD=DC,
∴∠C=∠CBD,
设∠C=∠CBD=x,
则∠BDA=∠A=2x,
∴∠ABD=180°﹣4x,
∴∠ABC=∠ABD+∠CBD=180°﹣4x+x=105°,
解得:x=25°,
所以2x=50°,
即∠A=50°,∠C=25°.
22.(8分)某中学的小明和朱老师一起到一条笔直的跑道上锻炼身体,到达起点后小明做了一会准备活动,朱老师先跑.当小明出发时,朱老师已经距起点200米了,他们距起点的距离s(米)与小明出发的时间t(秒)之间的关系如图所示(不完整),根据图中给出的信息,解答下列问题:
(1)在上述变化过程中,自变量是
t ,因变量是
;
(2)求小明和朱老师的速度;
(3)小明与朱老师相遇
2 次,相遇时距起点的距离分别为
300和420 米.
【解答】解:(1)观察函数图象可得出:自变量为小明出发的时间t,因变量为距起点的距离s.
故答案为:t,s;
(2)朱老师的速度为:(300﹣200)÷50=2(米/秒);
小明的速度为:300÷50=6(米/秒).
答:朱老师的速度为2米/秒,小明的速度为6米/秒;
(3)由图象得:小明与朱老师相遇2次,相遇时距起点的距离分别为300和420米,
故答案为:2,300和420.
23.(10分)如图,在Rt△ABC中,∠BAC=90°,AC=2AB,点D是AC的中点.将一块锐角为45°的直角三角板如图放置,使三角板斜边的两个端点分别与A、D重合,连接BE、EC.试猜想线段BE和EC的数量及位置关系,并证明你的猜想.
【解答】数量关系为:BE=EC,位置关系是:BE⊥EC.
证明:∵△AED是直角三角形,∠AED=90°,且有一个锐角是45°,
∴∠EAD=∠EDA=45°,
∴AE=DE,
∵∠BAC=90°,
∴∠EAB=∠EAD+∠BAC=45°+90°=135°,
∠EDC=∠ADC﹣∠EDA=180°﹣45°=135°,
∴∠EAB=∠EDC,
∵D是AC的中点,
∴AD=CD=AC,
∵AC=2AB,
∴AB=AD=DC,
∵在△EAB和△EDC中
,
∴△EAB≌△EDC(SAS),
∴EB=EC,且∠AEB=∠DEC,
∴∠BEC=∠DEC+∠BED=∠AEB+∠BED=90°,
∴BE⊥EC.
24.(10分)如图1所示,在△ABC中,AB=AC,AB的垂直平分线交AB于点N,交BC或BC的延长线于点M.
(1)如图1所示,若∠A=40°,求∠NMB的大小;
(2)如图2所示,如果将(1)中的∠A的度数改为70°,其余条件不变,再求∠NMB的大小;
(3)你发现了什么规律?写出猜想,并说明理由.
【解答】解:(1)∵AB=AC,∠A=40°,
∴∠ABC=∠ACB=,(180°﹣∠A)=70°,
∵MN是AB的垂直平分线,
∴∠MNB=90°,
∴∠NMB=90°﹣∠B=20°.
(2)∵AB=AC,∠A=70°,
∴∠B=∠ACB=(180°﹣∠A)=55°,
∵MN是AB的垂直平分线,
∴∠MNB=90°,
∴∠NMB=90°﹣∠B=35°.
(3)∠NMB=∠A,
理由是:∵AB=AC,
∴∠B=∠ACB=(180°﹣∠A)=90°﹣∠A,
∵MN是AB的垂直平分线,
∴∠MNB=90°,
∴∠NMB=90°﹣∠B=90°﹣(90°﹣∠A)=∠A.
第1页(共3页)
一、选择题(每题3分,共24分)
1.(3分)下列交通标志图案是轴对称图形的是( )
A.
B.
C.
D.
2.(3分)下列说法中不正确的是( )
A.“某射击运动员射击一次,正中靶心”属于随机事件
B.“13名同学至少有两名同学的出生月份相同”属于必然事件
C.“在标准大气压下,当温度降到﹣1℃时,水结成冰”属于随机事件
D.“某袋中只有5个球,且都是黄球,任意摸出一球是白球”属于不可能事件
3.(3分)下列计算错误的有( )
①(2x+y)2=4x2+y2
②(3b﹣a)2=9b2﹣a2
③(﹣3b﹣a)(a﹣3b)=a2﹣9b2
④(﹣x﹣y)2=x2﹣2xy+y2
⑤(x﹣)2=x2﹣x+.
A.1个
B.2个
C.3个
D.4个
4.(3分)如图是一个风筝的图案,它是以直线AF为对称轴的轴对称图形,下列结论中不一定成立的是( )
A.△ABD≌△ACD
B.AF垂直平分EG
C.直线BG,CE的交点在AF上
D.△DEG是等边三角形
5.(3分)如图,将长方形纸片的一角折叠,使顶点A落在点A′处,BC为折痕,若BE是∠A′BD的平分线,则∠CBE的度数是( )
A.65度
B.115度
C.90度
D.75度
6.(3分)有3cm,6cm,8cm,9cm的四条线段,任选其中的三条线段组成一个三角形,则最多能组成三角形的个数为( )
A.1
B.2
C.3
D.4
7.(3分)如图所示,AB=AC,AD=AE,∠BAC=∠DAE,∠1=25°,∠2=30°,则∠3=( )
A.55°
B.50°
C.45°
D.60°
8.(3分)如图所示,半径为1的圆和边长为3的正方形在同一水平线上,圆沿该水平线从左向右匀速穿过正方形,设穿过时间为t,正方形除去圆部分的面积为S(阴影部分),则S与t的大致图象为( )
A.
B.
C.
D.
二、填空题(每题3分,共18分)
9.(3分)把(6×105)2的结果用科学记数法表示为
.
10.(3分)如图,在△ABC中,AB=AC,点D是BC的中点,∠BAD=20°,则∠BAC=
度.
11.(3分)如图,直线a,b都垂直于直线c,直线d与a,b相交.若∠1=135°,则∠2=
°.
12.(3分)某校学生会提倡双休日到养老院参加服务活动,首次活动需要7位同学参加,现有包括小杰在内的50位同学报名,因此学生会将从这50位同学中随机抽取7位,小杰被抽到参加首次活动的概率是
.
13.(3分)若
(x+3)(x﹣4)=ax2+bx+c,则a=
、b=
、c=
.
14.(3分)如图,将一副三角板和一张对边平行的纸条按如图方式摆放,两个三角板的一直角边重合,含30°角的直角三角板的斜边与纸条一边重合,含45°角的三角板的一个顶点在纸条的另一边上,则∠1的度数是
.
三、解答题(共78分)
15.(6分)计算或化简:
(1)|﹣3|+(﹣1)2017×(π﹣3)0﹣()﹣3;
(2)(2a3b2﹣4a4b3+6a5b4)+(﹣2a3b2).
16.(6分)先化简,再求值:(3x+2y)2﹣(3x﹣2y)2+2(x+y)(x﹣y)﹣2(x+4y),其中x=1,y=﹣1.
17.(6分)如图,AD、BC相交于点O,OA=OC,∠OBD=∠ODB.求证:AB=CD.
18.(8分)如图,已知AB∥CD,DA平分∠BDC,∠A=∠C.
(1)试说明:CE∥AD;
(2)若∠C=30°,求∠B的度数.
19.(8分)某商人制成了一个如图所示的转盘游戏,取名为“开心大转盘”,游戏规定:参与者自由转动转盘,若指针指向字母“A”,则收费2元,若指针指向字母“B”,则奖3元;若指针指向字母“C”,则奖1元.一天,前来寻开心的人转动转盘80次,你认为该商人是盈利的可能性大还是亏损的可能性大?为什么?
20.(8分)如图,点B、F、C、E在同一直线上,并且BF=CE,∠B=∠E.
(1)请你只添加一个条件(不再加辅助线),使得△ABC≌△DEF.你添加的条件是:
.
(2)添加了条件后,证明△ABC≌△DEF.
21.(8分)如图,已知△ABC中,AB=BD=DC,∠ABC=105°,求∠A,∠C的度数.
22.(8分)某中学的小明和朱老师一起到一条笔直的跑道上锻炼身体,到达起点后小明做了一会准备活动,朱老师先跑.当小明出发时,朱老师已经距起点200米了,他们距起点的距离s(米)与小明出发的时间t(秒)之间的关系如图所示(不完整),根据图中给出的信息,解答下列问题:
(1)在上述变化过程中,自变量是
,因变量是
;
(2)求小明和朱老师的速度;
(3)小明与朱老师相遇
次,相遇时距起点的距离分别为
米.
23.(10分)如图,在Rt△ABC中,∠BAC=90°,AC=2AB,点D是AC的中点.将一块锐角为45°的直角三角板如图放置,使三角板斜边的两个端点分别与A、D重合,连接BE、EC.试猜想线段BE和EC的数量及位置关系,并证明你的猜想.
24.(10分)如图1所示,在△ABC中,AB=AC,AB的垂直平分线交AB于点N,交BC或BC的延长线于点M.
(1)如图1所示,若∠A=40°,求∠NMB的大小;
(2)如图2所示,如果将(1)中的∠A的度数改为70°,其余条件不变,再求∠NMB的大小;
(3)你发现了什么规律?写出猜想,并说明理由.
2020-2021学年山东省菏泽市鄄城县七年级(下)期末数学试卷
参考答案与试题解析
一、选择题(每题3分,共24分)
1.(3分)下列交通标志图案是轴对称图形的是( )
A.
B.
C.
D.
【解答】解:A、不是轴对称图形,故本选项错误;
B、是轴对称图形,故本选项正确;
C、不是轴对称图形,故本选项错误;
D、不是轴对称图形,故本选项错误;
故选:B.
2.(3分)下列说法中不正确的是( )
A.“某射击运动员射击一次,正中靶心”属于随机事件
B.“13名同学至少有两名同学的出生月份相同”属于必然事件
C.“在标准大气压下,当温度降到﹣1℃时,水结成冰”属于随机事件
D.“某袋中只有5个球,且都是黄球,任意摸出一球是白球”属于不可能事件
【解答】解:A、“某射击运动员射击一次,正中靶心”属于随机事件,正确;
B、“13名同学至少有两名同学的出生月份相同”属于必然事件,正确;
C、在标准大气压下,当温度降到﹣1℃时,水结成冰”属于必然事件;
D、“某袋中只有5个球,且都是黄球,任意摸出一球是白球”属于不可能事件,正确.
故选:C.
3.(3分)下列计算错误的有( )
①(2x+y)2=4x2+y2
②(3b﹣a)2=9b2﹣a2
③(﹣3b﹣a)(a﹣3b)=a2﹣9b2
④(﹣x﹣y)2=x2﹣2xy+y2
⑤(x﹣)2=x2﹣x+.
A.1个
B.2个
C.3个
D.4个
【解答】解:①(2x+y)2=4x2+4xy+y2,本选项错误;
②(3b﹣a)2=9b2﹣6ab+a2,本选项错误;
③(﹣3b﹣a)(a﹣3b)=9b2﹣a2,本选项错误;
④(﹣x﹣y)2=(x+y)2=x2+2xy+y2,本选项错误;
⑤(x﹣)2=x2﹣x+,本选项正确,
则错误的个数为4个.
故选:D.
4.(3分)如图是一个风筝的图案,它是以直线AF为对称轴的轴对称图形,下列结论中不一定成立的是( )
A.△ABD≌△ACD
B.AF垂直平分EG
C.直线BG,CE的交点在AF上
D.△DEG是等边三角形
【解答】解:A、因为此图形是轴对称图形,正确;
B、对称轴垂直平分对应点连线,正确;
C、由三角形全等可知,BG=CE,且直线BG,CE的交点在AF上,正确;
D、题目中没有60°条件,不能判断是等边三角形,错误.
故选:D.
5.(3分)如图,将长方形纸片的一角折叠,使顶点A落在点A′处,BC为折痕,若BE是∠A′BD的平分线,则∠CBE的度数是( )
A.65度
B.115度
C.90度
D.75度
【解答】解:由折叠的性质,∠ABC=∠A′BC,
∵BE是∠A′BD的平分线,
∴∠EBA′=∠EBD,
∴∠CBE=2(∠A′BC+∠EBA′)÷2=180°÷2=90°
故选:C.
6.(3分)有3cm,6cm,8cm,9cm的四条线段,任选其中的三条线段组成一个三角形,则最多能组成三角形的个数为( )
A.1
B.2
C.3
D.4
【解答】解:四条木棒的所有组合:3,6,8和3,6,9和6,8,9和3,8,9;
只有3,6,8和6,8,9;3,8,9能组成三角形.
故选:C.
7.(3分)如图所示,AB=AC,AD=AE,∠BAC=∠DAE,∠1=25°,∠2=30°,则∠3=( )
A.55°
B.50°
C.45°
D.60°
【解答】解:∵∠BAC=∠DAE,
∴∠BAC﹣∠DAC=∠DAE﹣∠DAC,
∴∠1=∠EAC,
在△BAD和△EAC中,,
∴△BAD≌△EAC(SAS),
∴∠2=∠ABD=30°,
∵∠1=25°,
∴∠3=∠1+∠ABD=25°+30°=55°,
故选:A.
8.(3分)如图所示,半径为1的圆和边长为3的正方形在同一水平线上,圆沿该水平线从左向右匀速穿过正方形,设穿过时间为t,正方形除去圆部分的面积为S(阴影部分),则S与t的大致图象为( )
A.
B.
C.
D.
【解答】解:由图中可知:在开始的时候,阴影部分的面积最大,可以排除B,C.
随着圆的穿行开始,阴影部分的面积开始减小,当圆完全进入正方形时,阴影部分的面积开始不再变化.应排除D.
故选:A.
二、填空题(每题3分,共18分)
9.(3分)把(6×105)2的结果用科学记数法表示为
3.6×1011 .
【解答】解:(6×105)2
=62×(105)2
=36×1010
=3.6×1011.
故答案为:3.6×1011.
10.(3分)如图,在△ABC中,AB=AC,点D是BC的中点,∠BAD=20°,则∠BAC= 40 度.
【解答】解:∵AB=CA,
∴△ABC是等腰三角形,
∵D是BC边上的中点,
∴AD平分∠BAC,
∵∠BAD=20°.
∴∠BAC=2×20°=40°.
故答案为:40.
11.(3分)如图,直线a,b都垂直于直线c,直线d与a,b相交.若∠1=135°,则∠2= 45 °.
【解答】解:如图,
∵a⊥c、b⊥c,
∴a∥b,
∵∠1=∠3=135°,
∴∠2+∠3=180°,
则∠3=45°,
故答案为:45.
12.(3分)某校学生会提倡双休日到养老院参加服务活动,首次活动需要7位同学参加,现有包括小杰在内的50位同学报名,因此学生会将从这50位同学中随机抽取7位,小杰被抽到参加首次活动的概率是 .
【解答】解:∵学生会将从这50位同学中随机抽取7位,
∴小杰被抽到参加首次活动的概率是:.
故答案为:.
13.(3分)若
(x+3)(x﹣4)=ax2+bx+c,则a= 1 、b= ﹣1 、c= ﹣12 .
【解答】解:∵(x+3)(x﹣4)=x2﹣x﹣12,
(x+3)(x﹣4)=ax2+bx+c,
∴ax2+bx+c=x2﹣x﹣12,
∴a=1,b=﹣1,c=﹣12.
故答案为1,﹣1,﹣12.
14.(3分)如图,将一副三角板和一张对边平行的纸条按如图方式摆放,两个三角板的一直角边重合,含30°角的直角三角板的斜边与纸条一边重合,含45°角的三角板的一个顶点在纸条的另一边上,则∠1的度数是
15° .
【解答】解:如图,过A点作AB∥a,
∴∠1=∠2,
∵a∥b,
∴AB∥b,
∴∠3=∠4=30°,
而∠2+∠3=45°,
∴∠2=15°,
∴∠1=15°.
故答案为15°.
三、解答题(共78分)
15.(6分)计算或化简:
(1)|﹣3|+(﹣1)2017×(π﹣3)0﹣()﹣3;
(2)(2a3b2﹣4a4b3+6a5b4)+(﹣2a3b2).
【解答】解(1)|﹣3|+(﹣1)2017×(π﹣3)0﹣()﹣3
=3+(﹣1)×1﹣(﹣8)
=3﹣1+8
=10.
(2)(2a3b2﹣4a4b3+6a5b4)+(﹣2a3b2)
=2a3b2﹣4a4b3+6a5b4﹣2a3b2
=(2a3b2﹣2a3b2)+(﹣4a4b3+6a5b4)
=0+(﹣4a4b3+6a5b4)
=﹣4a4b3+6a5b4.
16.(6分)先化简,再求值:(3x+2y)2﹣(3x﹣2y)2+2(x+y)(x﹣y)﹣2(x+4y),其中x=1,y=﹣1.
【解答】解:(3x+2y)2﹣(3x﹣2y)2+2(x+y)(x﹣y)﹣2(x+4y)
=9x2+12xy+4y2﹣9x2+12xy﹣4y2+2x2﹣2y2﹣2x﹣8y
=2x2+24xy﹣2y2﹣2x﹣8y,
当x=1,y=﹣1时,原式=2×12+24×1×(﹣1)﹣2×(﹣1)2﹣2×1﹣8×(﹣1)=﹣18.
17.(6分)如图,AD、BC相交于点O,OA=OC,∠OBD=∠ODB.求证:AB=CD.
【解答】证明:∵∠OBD=∠ODB.
∴OB=OD,
在△AOB与△COD中,
∴△AOB≌△COD(SAS)
∴AB=CD.
18.(8分)如图,已知AB∥CD,DA平分∠BDC,∠A=∠C.
(1)试说明:CE∥AD;
(2)若∠C=30°,求∠B的度数.
【解答】解:(1)∵AB∥CD,
∴∠A=∠ADC.
∵∠A=∠C,
∴∠ADC=∠C,
∴CE∥AD;
(2)由(1)可得∠ADC=∠C=30°.
∵DA平分∠BDC,∠ADC=∠ADB,
∴∠CDB=2∠ADC=60°.
∵AB∥DC,
∴∠B+∠CDB=180°,
∴∠B=180°﹣∠CDB=120°.
19.(8分)某商人制成了一个如图所示的转盘游戏,取名为“开心大转盘”,游戏规定:参与者自由转动转盘,若指针指向字母“A”,则收费2元,若指针指向字母“B”,则奖3元;若指针指向字母“C”,则奖1元.一天,前来寻开心的人转动转盘80次,你认为该商人是盈利的可能性大还是亏损的可能性大?为什么?
【解答】解:商人盈利的可能性大
PA=80×=40(次);
PB=80×=10(次);
PC=80×=30(次);
理由:商人盈利:(元)
商人亏损:=60(元)
因为80>60
所以商人盈利的可能性大.
20.(8分)如图,点B、F、C、E在同一直线上,并且BF=CE,∠B=∠E.
(1)请你只添加一个条件(不再加辅助线),使得△ABC≌△DEF.你添加的条件是: ∠A=∠D .
(2)添加了条件后,证明△ABC≌△DEF.
【解答】解:(1)故答案为:∠A=∠D.
(2)证明:∵BF=CE,
∴BF+FC=EC+FC,
∴在△ABC和△DEF中,
,
∴△ABC≌△DEF(AAS)
21.(8分)如图,已知△ABC中,AB=BD=DC,∠ABC=105°,求∠A,∠C的度数.
【解答】解:∵AB=BD,
∴∠BDA=∠A,
∵BD=DC,
∴∠C=∠CBD,
设∠C=∠CBD=x,
则∠BDA=∠A=2x,
∴∠ABD=180°﹣4x,
∴∠ABC=∠ABD+∠CBD=180°﹣4x+x=105°,
解得:x=25°,
所以2x=50°,
即∠A=50°,∠C=25°.
22.(8分)某中学的小明和朱老师一起到一条笔直的跑道上锻炼身体,到达起点后小明做了一会准备活动,朱老师先跑.当小明出发时,朱老师已经距起点200米了,他们距起点的距离s(米)与小明出发的时间t(秒)之间的关系如图所示(不完整),根据图中给出的信息,解答下列问题:
(1)在上述变化过程中,自变量是
t ,因变量是
;
(2)求小明和朱老师的速度;
(3)小明与朱老师相遇
2 次,相遇时距起点的距离分别为
300和420 米.
【解答】解:(1)观察函数图象可得出:自变量为小明出发的时间t,因变量为距起点的距离s.
故答案为:t,s;
(2)朱老师的速度为:(300﹣200)÷50=2(米/秒);
小明的速度为:300÷50=6(米/秒).
答:朱老师的速度为2米/秒,小明的速度为6米/秒;
(3)由图象得:小明与朱老师相遇2次,相遇时距起点的距离分别为300和420米,
故答案为:2,300和420.
23.(10分)如图,在Rt△ABC中,∠BAC=90°,AC=2AB,点D是AC的中点.将一块锐角为45°的直角三角板如图放置,使三角板斜边的两个端点分别与A、D重合,连接BE、EC.试猜想线段BE和EC的数量及位置关系,并证明你的猜想.
【解答】数量关系为:BE=EC,位置关系是:BE⊥EC.
证明:∵△AED是直角三角形,∠AED=90°,且有一个锐角是45°,
∴∠EAD=∠EDA=45°,
∴AE=DE,
∵∠BAC=90°,
∴∠EAB=∠EAD+∠BAC=45°+90°=135°,
∠EDC=∠ADC﹣∠EDA=180°﹣45°=135°,
∴∠EAB=∠EDC,
∵D是AC的中点,
∴AD=CD=AC,
∵AC=2AB,
∴AB=AD=DC,
∵在△EAB和△EDC中
,
∴△EAB≌△EDC(SAS),
∴EB=EC,且∠AEB=∠DEC,
∴∠BEC=∠DEC+∠BED=∠AEB+∠BED=90°,
∴BE⊥EC.
24.(10分)如图1所示,在△ABC中,AB=AC,AB的垂直平分线交AB于点N,交BC或BC的延长线于点M.
(1)如图1所示,若∠A=40°,求∠NMB的大小;
(2)如图2所示,如果将(1)中的∠A的度数改为70°,其余条件不变,再求∠NMB的大小;
(3)你发现了什么规律?写出猜想,并说明理由.
【解答】解:(1)∵AB=AC,∠A=40°,
∴∠ABC=∠ACB=,(180°﹣∠A)=70°,
∵MN是AB的垂直平分线,
∴∠MNB=90°,
∴∠NMB=90°﹣∠B=20°.
(2)∵AB=AC,∠A=70°,
∴∠B=∠ACB=(180°﹣∠A)=55°,
∵MN是AB的垂直平分线,
∴∠MNB=90°,
∴∠NMB=90°﹣∠B=35°.
(3)∠NMB=∠A,
理由是:∵AB=AC,
∴∠B=∠ACB=(180°﹣∠A)=90°﹣∠A,
∵MN是AB的垂直平分线,
∴∠MNB=90°,
∴∠NMB=90°﹣∠B=90°﹣(90°﹣∠A)=∠A.
第1页(共3页)
同课章节目录
