4.2 解一元一次方程课件(共40张PPT)
文档属性
| 名称 | 4.2 解一元一次方程课件(共40张PPT) |
|
|
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-06 00:00:00 | ||
图片预览











文档简介
(共40张PPT)
第四章
一元一次方程
2
解一元一次方程
知识点一
移项
定义
依据
目的
移项
重要提示
知识点一
移项
定义
依据
目的
移项
把等式一边的某项变号后移到另一边,叫做移项
重要提示
知识点一
移项
定义
依据
目的
移项
把等式一边的某项变号后移到另一边,叫做移项
等式的基本性质1
重要提示
知识点一
移项
定义
依据
目的
移项
把等式一边的某项变号后移到另一边,叫做移项
等式的基本性质1
将含有未知数的项移到方程的一边,将不含未知数的项移到方程的另一边,使方程更接近于x=a(a为常数)的形式
重要提示
知识点一
移项
定义
依据
目的
移项
把等式一边的某项变号后移到另一边,叫做移项
等式的基本性质1
将含有未知数的项移到方程的一边,将不含未知数的项移到方程的另一边,使方程更接近于x=a(a为常数)的形式
重要提示
1.移项的项一定要改变符号;
2.将3=x变形为x=3,利用的是等式的对称性,不需要改变符号
例1
对于方程-3x-7=12x+6,下列移项正确的是(
)
A.-3x-12x=6+7
B.-3x+12x=-7+6
C.-3x-12x=7-6
D.12x-3x=6+7
例1
对于方程-3x-7=12x+6,下列移项正确的是(
)
A.-3x-12x=6+7
B.-3x+12x=-7+6
C.-3x-12x=7-6
D.12x-3x=6+7
解析
把12x改变符号后从右边移到左边,-7改变符号后从左边移到右边,得-3x-12x=6+7,故选A.
例1
对于方程-3x-7=12x+6,下列移项正确的是(
)
A.-3x-12x=6+7
B.-3x+12x=-7+6
C.-3x-12x=7-6
D.12x-3x=6+7
解析
把12x改变符号后从右边移到左边,-7改变符号后从左边移到右边,得-3x-12x=6+7,故选A.
特别提示
移项时,只改变移动的项的符号,不要改变未移动的项的符号.
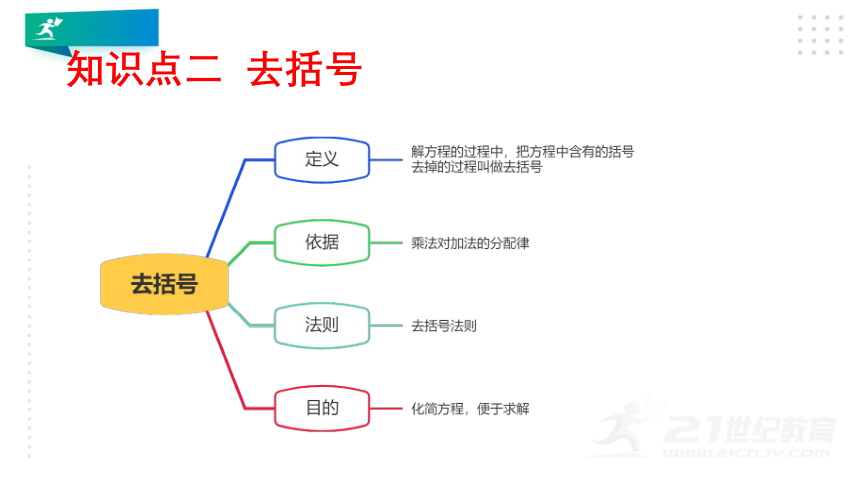
知识点二
去括号
例2
解方程:4(x-2)=2-(x-5).
例2
解方程:4(x-2)=2-(x-5).
解析
去括号,得4x-8=2-x+5,
移项,得4x+x=2+5+8,
合并同类项,得5x=15,
系数化为1,得x=3.
例2
解方程:4(x-2)=2-(x-5).
解析
去括号,得4x-8=2-x+5,
移项,得4x+x=2+5+8,
合并同类项,得5x=15,
系数化为1,得x=3.
特别提示
去括号时,括号前是负号,去掉括号后要改变括号内各项的符号.
知识点三
解一元一次方程的步骤
知识点三
解一元一次方程的步骤
步骤
具体做法
依据
注意事项
去分母
去括号
移项
合并同类项
系数化为1
知识点三
解一元一次方程的步骤
步骤
具体做法
依据
注意事项
去分母
在方程两边都乘各分数的分母的最小公倍数
等式的基本性质2
不要漏乘不含分母的项;分数线的括号作用
去括号
移项
合并同类项
系数化为1
知识点三
解一元一次方程的步骤
步骤
具体做法
依据
注意事项
去分母
在方程两边都乘各分数的分母的最小公倍数
等式的基本性质2
不要漏乘不含分母的项;分数线的括号作用
去括号
一般先去小括号,再去中括号,最后去大括号
乘法对加法的分配律,去括号法则
分配律要满足分配到每一项
移项
合并同类项
系数化为1
知识点三
解一元一次方程的步骤
步骤
具体做法
依据
注意事项
去分母
在方程两边都乘各分数的分母的最小公倍数
等式的基本性质2
不要漏乘不含分母的项;分数线的括号作用
去括号
一般先去小括号,再去中括号,最后去大括号
乘法对加法的分配律,去括号法则
分配律要满足分配到每一项
移项
把含有未知数的项移到方程的一边,其他项移到另一边
等式的基本性质1
移项变号
合并同类项
系数化为1
知识点三
解一元一次方程的步骤
步骤
具体做法
依据
注意事项
去分母
在方程两边都乘各分数的分母的最小公倍数
等式的基本性质2
不要漏乘不含分母的项;分数线的括号作用
去括号
一般先去小括号,再去中括号,最后去大括号
乘法对加法的分配律,去括号法则
分配律要满足分配到每一项
移项
把含有未知数的项移到方程的一边,其他项移到另一边
等式的基本性质1
移项变号
合并同类项
把方程中的同类项分别合并,化成“ax=b(a≠0)”的形式
合并同类项法则
注意符号
系数化为1
知识点三
解一元一次方程的步骤
步骤
具体做法
依据
注意事项
去分母
在方程两边都乘各分数的分母的最小公倍数
等式的基本性质2
不要漏乘不含分母的项;分数线的括号作用
去括号
一般先去小括号,再去中括号,最后去大括号
乘法对加法的分配律,去括号法则
分配律要满足分配到每一项
移项
把含有未知数的项移到方程的一边,其他项移到另一边
等式的基本性质1
移项变号
合并同类项
把方程中的同类项分别合并,化成“ax=b(a≠0)”的形式
合并同类项法则
注意符号
系数化为1
方程两边同时除以未知数的系数得x=
等式的基本性质2
分子、分母不能颠倒位置
例3
解方程:.
例3
解方程:.
解析
去分母,得10-2(x+2)=5(x-1),
去括号,得10-2x-4=5x-5,
移项,得-2x-5x=4-5-10,
合并同类项,得-7x=-11,
系数化为1,得x=.
例3
解方程:.
解析
去分母,得10-2(x+2)=5(x-1),
去括号,得10-2x-4=5x-5,
移项,得-2x-5x=4-5-10,
合并同类项,得-7x=-11,
系数化为1,得x=.
特别提示
去分母时,若分子是一个多项式,要加上括号,找准分母的最小公倍数,在用最小公倍数乘方程两边的每一项时,不要漏乘不含分母的项.
经典例题
题型一
含小数的一元一次方程的解法
例1
解方程:.
例1
解方程:.
解析
原方程可化为.
去分母,得3(2x-4)-15x=5(5x-20),
去括号,得6x-12-15x=25x-100,
移项,得6x-15x-25x=12-100,
合并同类项,得-34x=-88,
系数化为1,得x=.
例1
解方程:.
解析
原方程可化为.
去分母,得3(2x-4)-15x=5(5x-20),
去括号,得6x-12-15x=25x-100,
移项,得6x-15x-25x=12-100,
合并同类项,得-34x=-88,
系数化为1,得x=.
点拨
将小数化成整数,是根据分数的基本性质把含有小数的项的分子、分母乘同一个适当的数,而不是方程所有的项都乘这个数.小数化成整数,是对分母含小数的项的恒等变形,
题型二
根据同解方程求某个字母的值
例2
如果关于x的方程的解与方程4x-(3a+1)=6x+2a-1的解相同,求a的值.
例2
如果关于x的方程的解与方程4x-(3a+1)=6x+2a-1的解相同,求a的值.
分析
先求出第一个方程的解,然后代入第二个方程得到关于a的一元一次方程,再根据一元一次方程的解法进行求解即可,
例2
如果关于x的方程的解与方程4x-(3a+1)=6x+2a-1的解相同,求a的值.
分析
先求出第一个方程的解,然后代入第二个方程得到关于a的一元一次方程,再根据一元一次方程的解法进行求解即可,
解析
解方程,得x=10,
所以方程4x-(3a+1)=6x+2a-1的解为x=10,
把x=10代入方程4x-(3a+1)=6x+2a-1,
得4×10-(3a+1)=6×10+2a-1,
解得a=-4.
例2
如果关于x的方程的解与方程4x-(3a+1)=6x+2a-1的解相同,求a的值.
分析
先求出第一个方程的解,然后代入第二个方程得到关于a的一元一次方程,再根据一元一次方程的解法进行求解即可,
解析
解方程,得x=10,
所以方程4x-(3a+1)=6x+2a-1的解为x=10,
把x=10代入方程4x-(3a+1)=6x+2a-1,
得4×10-(3a+1)=6×10+2a-1,
解得a=-4.
特别提示
同解方程就是解相同的方程,本题先求出第一个方程的解是解题的关键.
易错易混
易错点
不理解解方程步骤的实质导致出错
在解一元一次方程时,因对去分母、去括号、移项等步骤的实质不理解而导致出错.
例题
解方程:
.
例题
解方程:
.
解析
去分母,得3x-6(x-1)+60=2(x+3).
去括号,得3x-6x+6+60=2x+6.
移项,得3x-6x-2x=6-6-60.
合并同类项,得-5x=-60.
系数化为1,得x=12.
例题
解方程:
.
解析
去分母,得3x-6(x-1)+60=2(x+3).
去括号,得3x-6x+6+60=2x+6.
移项,得3x-6x-2x=6-6-60.
合并同类项,得-5x=-60.
系数化为1,得x=12.
易错警示
(1)去分母时,常数项5易漏乘公分母12;
(2)去括号时,-1和3易漏乘.
第四章
一元一次方程
2
解一元一次方程
知识点一
移项
定义
依据
目的
移项
重要提示
知识点一
移项
定义
依据
目的
移项
把等式一边的某项变号后移到另一边,叫做移项
重要提示
知识点一
移项
定义
依据
目的
移项
把等式一边的某项变号后移到另一边,叫做移项
等式的基本性质1
重要提示
知识点一
移项
定义
依据
目的
移项
把等式一边的某项变号后移到另一边,叫做移项
等式的基本性质1
将含有未知数的项移到方程的一边,将不含未知数的项移到方程的另一边,使方程更接近于x=a(a为常数)的形式
重要提示
知识点一
移项
定义
依据
目的
移项
把等式一边的某项变号后移到另一边,叫做移项
等式的基本性质1
将含有未知数的项移到方程的一边,将不含未知数的项移到方程的另一边,使方程更接近于x=a(a为常数)的形式
重要提示
1.移项的项一定要改变符号;
2.将3=x变形为x=3,利用的是等式的对称性,不需要改变符号
例1
对于方程-3x-7=12x+6,下列移项正确的是(
)
A.-3x-12x=6+7
B.-3x+12x=-7+6
C.-3x-12x=7-6
D.12x-3x=6+7
例1
对于方程-3x-7=12x+6,下列移项正确的是(
)
A.-3x-12x=6+7
B.-3x+12x=-7+6
C.-3x-12x=7-6
D.12x-3x=6+7
解析
把12x改变符号后从右边移到左边,-7改变符号后从左边移到右边,得-3x-12x=6+7,故选A.
例1
对于方程-3x-7=12x+6,下列移项正确的是(
)
A.-3x-12x=6+7
B.-3x+12x=-7+6
C.-3x-12x=7-6
D.12x-3x=6+7
解析
把12x改变符号后从右边移到左边,-7改变符号后从左边移到右边,得-3x-12x=6+7,故选A.
特别提示
移项时,只改变移动的项的符号,不要改变未移动的项的符号.
知识点二
去括号
例2
解方程:4(x-2)=2-(x-5).
例2
解方程:4(x-2)=2-(x-5).
解析
去括号,得4x-8=2-x+5,
移项,得4x+x=2+5+8,
合并同类项,得5x=15,
系数化为1,得x=3.
例2
解方程:4(x-2)=2-(x-5).
解析
去括号,得4x-8=2-x+5,
移项,得4x+x=2+5+8,
合并同类项,得5x=15,
系数化为1,得x=3.
特别提示
去括号时,括号前是负号,去掉括号后要改变括号内各项的符号.
知识点三
解一元一次方程的步骤
知识点三
解一元一次方程的步骤
步骤
具体做法
依据
注意事项
去分母
去括号
移项
合并同类项
系数化为1
知识点三
解一元一次方程的步骤
步骤
具体做法
依据
注意事项
去分母
在方程两边都乘各分数的分母的最小公倍数
等式的基本性质2
不要漏乘不含分母的项;分数线的括号作用
去括号
移项
合并同类项
系数化为1
知识点三
解一元一次方程的步骤
步骤
具体做法
依据
注意事项
去分母
在方程两边都乘各分数的分母的最小公倍数
等式的基本性质2
不要漏乘不含分母的项;分数线的括号作用
去括号
一般先去小括号,再去中括号,最后去大括号
乘法对加法的分配律,去括号法则
分配律要满足分配到每一项
移项
合并同类项
系数化为1
知识点三
解一元一次方程的步骤
步骤
具体做法
依据
注意事项
去分母
在方程两边都乘各分数的分母的最小公倍数
等式的基本性质2
不要漏乘不含分母的项;分数线的括号作用
去括号
一般先去小括号,再去中括号,最后去大括号
乘法对加法的分配律,去括号法则
分配律要满足分配到每一项
移项
把含有未知数的项移到方程的一边,其他项移到另一边
等式的基本性质1
移项变号
合并同类项
系数化为1
知识点三
解一元一次方程的步骤
步骤
具体做法
依据
注意事项
去分母
在方程两边都乘各分数的分母的最小公倍数
等式的基本性质2
不要漏乘不含分母的项;分数线的括号作用
去括号
一般先去小括号,再去中括号,最后去大括号
乘法对加法的分配律,去括号法则
分配律要满足分配到每一项
移项
把含有未知数的项移到方程的一边,其他项移到另一边
等式的基本性质1
移项变号
合并同类项
把方程中的同类项分别合并,化成“ax=b(a≠0)”的形式
合并同类项法则
注意符号
系数化为1
知识点三
解一元一次方程的步骤
步骤
具体做法
依据
注意事项
去分母
在方程两边都乘各分数的分母的最小公倍数
等式的基本性质2
不要漏乘不含分母的项;分数线的括号作用
去括号
一般先去小括号,再去中括号,最后去大括号
乘法对加法的分配律,去括号法则
分配律要满足分配到每一项
移项
把含有未知数的项移到方程的一边,其他项移到另一边
等式的基本性质1
移项变号
合并同类项
把方程中的同类项分别合并,化成“ax=b(a≠0)”的形式
合并同类项法则
注意符号
系数化为1
方程两边同时除以未知数的系数得x=
等式的基本性质2
分子、分母不能颠倒位置
例3
解方程:.
例3
解方程:.
解析
去分母,得10-2(x+2)=5(x-1),
去括号,得10-2x-4=5x-5,
移项,得-2x-5x=4-5-10,
合并同类项,得-7x=-11,
系数化为1,得x=.
例3
解方程:.
解析
去分母,得10-2(x+2)=5(x-1),
去括号,得10-2x-4=5x-5,
移项,得-2x-5x=4-5-10,
合并同类项,得-7x=-11,
系数化为1,得x=.
特别提示
去分母时,若分子是一个多项式,要加上括号,找准分母的最小公倍数,在用最小公倍数乘方程两边的每一项时,不要漏乘不含分母的项.
经典例题
题型一
含小数的一元一次方程的解法
例1
解方程:.
例1
解方程:.
解析
原方程可化为.
去分母,得3(2x-4)-15x=5(5x-20),
去括号,得6x-12-15x=25x-100,
移项,得6x-15x-25x=12-100,
合并同类项,得-34x=-88,
系数化为1,得x=.
例1
解方程:.
解析
原方程可化为.
去分母,得3(2x-4)-15x=5(5x-20),
去括号,得6x-12-15x=25x-100,
移项,得6x-15x-25x=12-100,
合并同类项,得-34x=-88,
系数化为1,得x=.
点拨
将小数化成整数,是根据分数的基本性质把含有小数的项的分子、分母乘同一个适当的数,而不是方程所有的项都乘这个数.小数化成整数,是对分母含小数的项的恒等变形,
题型二
根据同解方程求某个字母的值
例2
如果关于x的方程的解与方程4x-(3a+1)=6x+2a-1的解相同,求a的值.
例2
如果关于x的方程的解与方程4x-(3a+1)=6x+2a-1的解相同,求a的值.
分析
先求出第一个方程的解,然后代入第二个方程得到关于a的一元一次方程,再根据一元一次方程的解法进行求解即可,
例2
如果关于x的方程的解与方程4x-(3a+1)=6x+2a-1的解相同,求a的值.
分析
先求出第一个方程的解,然后代入第二个方程得到关于a的一元一次方程,再根据一元一次方程的解法进行求解即可,
解析
解方程,得x=10,
所以方程4x-(3a+1)=6x+2a-1的解为x=10,
把x=10代入方程4x-(3a+1)=6x+2a-1,
得4×10-(3a+1)=6×10+2a-1,
解得a=-4.
例2
如果关于x的方程的解与方程4x-(3a+1)=6x+2a-1的解相同,求a的值.
分析
先求出第一个方程的解,然后代入第二个方程得到关于a的一元一次方程,再根据一元一次方程的解法进行求解即可,
解析
解方程,得x=10,
所以方程4x-(3a+1)=6x+2a-1的解为x=10,
把x=10代入方程4x-(3a+1)=6x+2a-1,
得4×10-(3a+1)=6×10+2a-1,
解得a=-4.
特别提示
同解方程就是解相同的方程,本题先求出第一个方程的解是解题的关键.
易错易混
易错点
不理解解方程步骤的实质导致出错
在解一元一次方程时,因对去分母、去括号、移项等步骤的实质不理解而导致出错.
例题
解方程:
.
例题
解方程:
.
解析
去分母,得3x-6(x-1)+60=2(x+3).
去括号,得3x-6x+6+60=2x+6.
移项,得3x-6x-2x=6-6-60.
合并同类项,得-5x=-60.
系数化为1,得x=12.
例题
解方程:
.
解析
去分母,得3x-6(x-1)+60=2(x+3).
去括号,得3x-6x+6+60=2x+6.
移项,得3x-6x-2x=6-6-60.
合并同类项,得-5x=-60.
系数化为1,得x=12.
易错警示
(1)去分母时,常数项5易漏乘公分母12;
(2)去括号时,-1和3易漏乘.
