1.2.1函数的概念(新课标A版)
文档属性
| 名称 | 1.2.1函数的概念(新课标A版) |

|
|
| 格式 | zip | ||
| 文件大小 | 798.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-07-31 00:00:00 | ||
图片预览






文档简介
(共35张PPT)
f :A→B
y=f(x),
1.2.1 函数的概念
远距离航海中对经度与纬度的测量用到函数
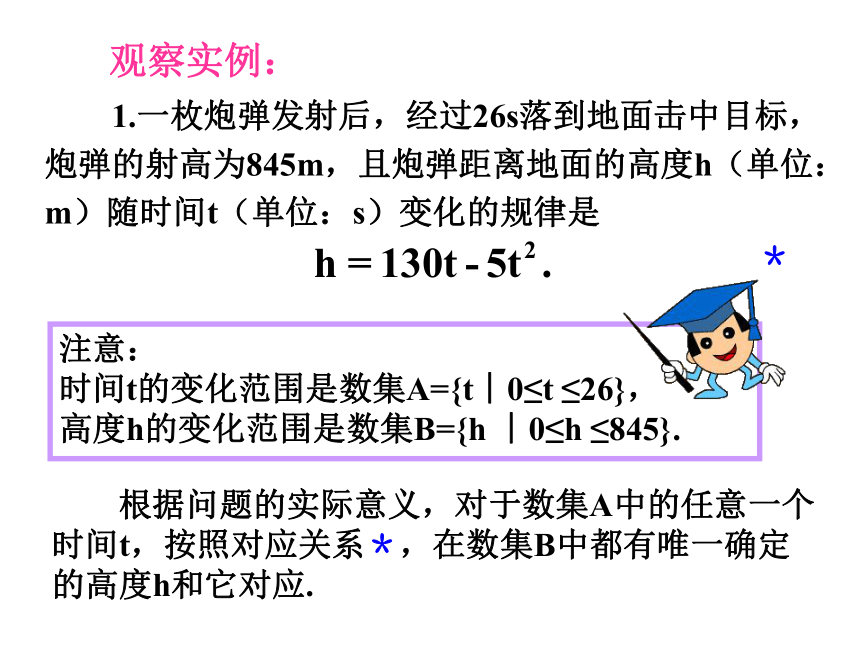
1.一枚炮弹发射后,经过26s落到地面击中目标,炮弹的射高为845m,且炮弹距离地面的高度h(单位:m)随时间t(单位:s)变化的规律是
根据问题的实际意义,对于数集A中的任意一个时间t,按照对应关系*,在数集B中都有唯一确定的高度h和它对应.
*
观察实例:
注意:
时间t的变化范围是数集A={t︱0≤t ≤26},
高度h的变化范围是数集B={h ︱0≤h ≤845}.
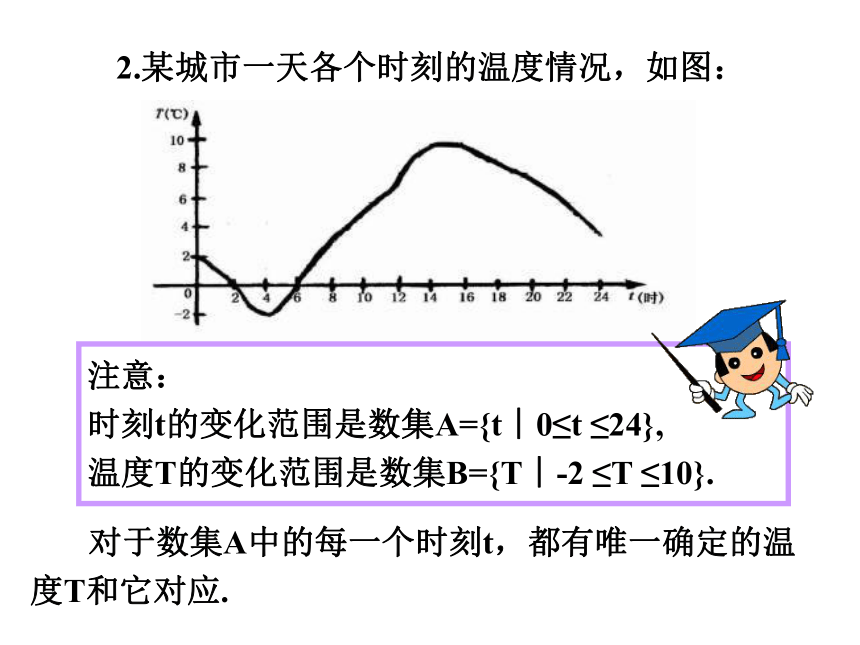
2.某城市一天各个时刻的温度情况,如图:
对于数集A中的每一个时刻t,都有唯一确定的温度T和它对应.
注意:
时刻t的变化范围是数集A={t︱0≤t ≤24},
温度T的变化范围是数集B={T︱-2 ≤T ≤10}.
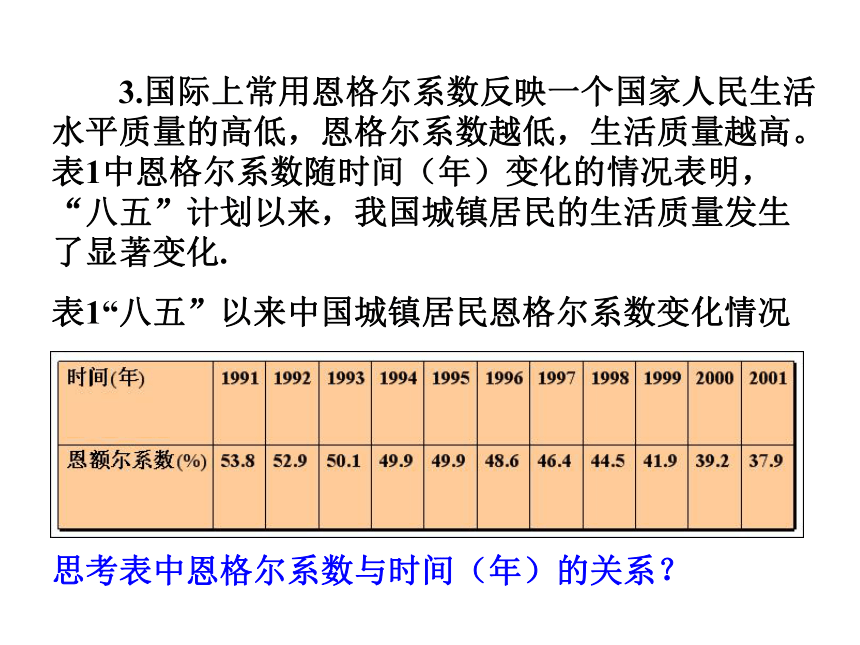
3.国际上常用恩格尔系数反映一个国家人民生活水平质量的高低,恩格尔系数越低,生活质量越高。表1中恩格尔系数随时间(年)变化的情况表明,“八五”计划以来,我国城镇居民的生活质量发生了显著变化.
表1“八五”以来中国城镇居民恩格尔系数变化情况
思考表中恩格尔系数与时间(年)的关系?
注意:
时间t的变化范围是数集A={t︱1998≤t ≤2005}
恩格尔系数k的变化范围是数集
B={k︱37.9 ≤k ≤50.1}.
对于数集A中每个年份t,在数集B中都有唯一确定的恩格尔系数与它对应.
以上例子中,变量之间的关系有什么共同的特点呢?
对于集合A中的每个x,按照某种关系f,在数集B中都有唯一确定的y与它对应。
记作:f: A→B.
设A,B是非空的数集,如果按照某种确定的对应关系f,使对集合A中的任意一个数x,在集合B中都有唯一确定的数f(x)和它对应,那么就称f:A→B为从集合A到B的一个函数.记作
y=f(x),x∈A
其中x叫做自变量,x的取值范围A叫做函数的定义域
与x的值相对应的y值叫做函数值,函数值的集合 {f(x)|x∈A} 叫做函数的值域.
知识要点
(1)要求必须是非空集合A,B;
(2)必须是集合A中的任意一个x;
(3)必须是在集合B中有唯一确定的数与之相对应;
(4) “y= f(x)”是函数符号,可以用任意的字母表示,
如“y= g(x)”;
(5)函数符号“y= f(x)”中的 f(x)表示与x对应的函数
值,一个数,而不是f乘x.
注意
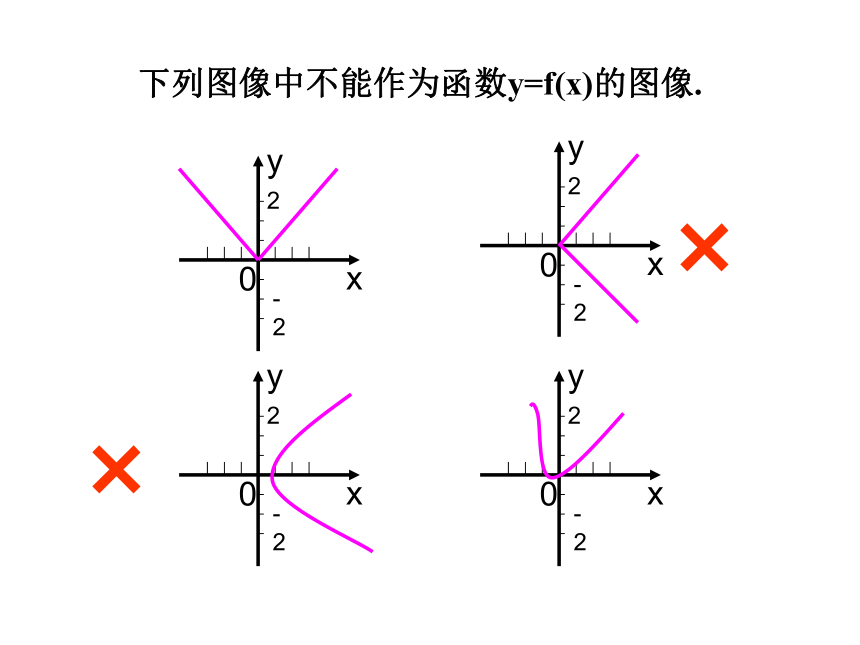
下列图像中不能作为函数y=f(x)的图像.
x
y
0
2
-2
x
y
0
2
-2
x
y
0
2
-2
x
y
0
2
-2
×
×
下列函数的定义域,对应关系,值域.
定义域是R,值域是R
对于R中的任意一个数x,在R中都有唯一确定的数y=ax+b(a≠0)和它对应.
思考
定义域是A={ ︱x≠0 },值域是R.
对于集合A中的每一个x,在R中都有唯一确定的值 与它对应.
定义域是R,值域是集合B,当a>0时,B={y︱y≥ },当a<0时,B={y︱y≤ }.
对于R中的任意一个数x,在B中都有唯一确定的
和它对应.
构成函数的三要素是定义域、对应关系和值域.
与函数相关的概念——区间
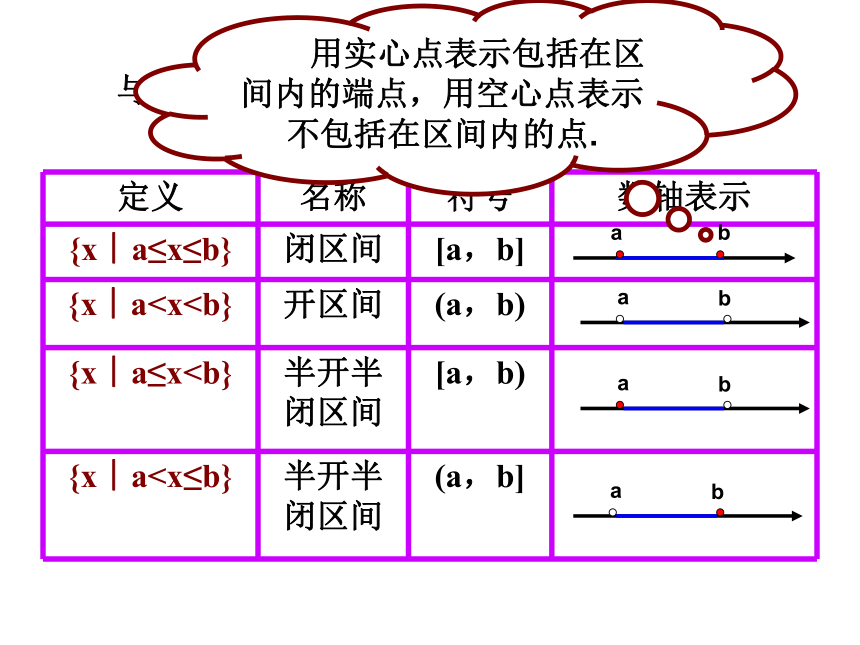
定义 名称 符号 数轴表示
{x︱a≤x≤b} 闭区间 [a,b]
{x︱a{x︱a≤x半开半闭区间 [a,b)
{x︱a半开半闭区间 (a,b]
a
b
a
b
a
b
a
b
用实心点表示包括在区间内的端点,用空心点表示不包括在区间内的点.
集合 符号 数轴表示
R
{x︱x≥a}
{x︱x>a}
{x︱x ≤ b}
{x︱x < b}
a
a
b
b
做一做
(-∞,+ ∞)
[a,+ ∞)
(a,+ ∞ )
(- ∞,b]
(- ∞,b)
(1)区间是集合;
(2)区间的左端点小于右端点;
(3)区间中的元素都是点,可以用数字表示;
(4)任何区间都可以在数轴上表示出来;
(5)以“-∞”,“+∞”为区间的一端时,这一端必须是小括号. 例如(+∞,100]
注意
例1 求下列函数的定义域
分析:函数的定义域通常是由问题的实际背景确定,如果单纯的给出解析式y=f(x),没有指明定义域,那么函数的定义域就是使这个式子有意义的实数的集合.
解:(1)使 有意义,就是 ,即使分数有意义的集合是{x︱x<0},所以这个函数的定义域就是{x︱x<0}.
(2)使根式 有意义的实数的集合是{x︱x≥-2},使分式 成立的实数的集合是{x︱x≠10}.所以,这个函数的定义域就是
{x︱x≥-2} {x︱x≠10}={x︱x ≥-2,且x≠10} .
例2 已知函数
(1)求f(-1),f(0)的值;
(2)当-1≤a ≤ 3时,求f(a)的值.
解:
且边长为正
数,所以0<x<40.
所以面积s=
= (40-x)x (0<x<40)
解: 由题意知,另一边长为
例3 设一个矩形周长为80,其中一边长为x,求它的面积关于x的函数的解析式,并写出定义域.
(1)如果f(x)是整式,那么函数的定义域是实数集R .
(2)如果f(x)是分式,那么函数的定义域是使分母不等于零的实数的集合 .
(3)如果f(x)是二次根式,那么函数的定义域是使根号内的式子大于或等于零的实数的集合.
(4)如果f(x)是由几个部分的数学式子构成的,那么函数定义域是使各部分式子都有意义的实数集合.(即求各集合的交集).
(5)满足实际问题有意义.
几类函数的定义域:
判断两个函数相等:
1 .构成函数三个要素是定义域、对应关系和值域.由于值域是由定义域和对应关系决定的,所以,如果两个函数的定义域和对应关系完全一致,即称这两个函数相等(或为同一函数).
2. 与表示自变量和函数值的字母无关.
知识要点
解: ① f ( x ) = (x -1) 0 =1,其定义域与 g ( x ) = 1的定义域是相同的,所以这两个函数是相等的.
② f ( x ) = x与函数g ( x ) = 的定义域都是实数R,但是当x<0时,它们的对应关系不相同。所以这两个函数不相等.
例4 判断下列函数f(x)与g(x)是否表示同一个函数,说明理由?
① f ( x ) = (x -1) 0;g ( x ) = 1
② f ( x ) = x; g ( x ) =
到现在为止,我们在初中学习的基础上,运用集合和对应的语言刻画了函数的概念,并引进了符号y=f(x),明确了函数的构成要素.通过比较两个函数的定义,你对函数有什么新的认识
这两种定义在实质上是一致的,不同的只是叙述的出发点不同,初中给出的定义是从运动变化的观点出发,而现在所给的定义是从集合、对应的观点出发.
1.函数的概念
设A,B是非空的数集,如果按照某种确定的对应关系f,使对集合A中的任意一个数x,在集合B中都有唯一确定的数f(x)和它对应,那么就称f:A→B为从集合A到B的一个函数.记作
y=f(x),x∈A
其中x叫做自变量,x的取值范围A叫做函数的定义域,与x的值相对应的y值叫做函数值,函数值的集合 {f(x)|x∈A} 叫做函数的值域.
课堂小结
定义 名称 符号 数轴表示
{x︱a≤x≤b} 闭区间 [a,b]
{x︱a{x︱a≤x半开半闭区间 [a,b)
{x︱a半开半闭区间 (a,b]
a
b
a
b
a
b
a
b
与函数相关的概念——区间
2.构成函数的三要素
定义域、对应关系和值域.
3.判断两个函数相等
两个函数相等当且仅当它们的定义域和对应关系完全一致,而与表示自变量和函数值的字母无关.
1.已知函数 , 求
课堂练习
解:∵2>1
∴f(2)=-x+1 = -2+1 = -1
f[f(2)]=f(-1)=-1+2=1
2.求下列函数的定义域.
解:(1)使分式有意义的实数集合是
{x∣ 并且x≠1 },所以此函数的定义
域为{x ∣ x≠0且x≠1 } .
( 2 )使根式成立的实数集合是{x∣x≥-2},使分式有意义的实数集合{x∣x≠-1}所以此函数的定义域为{x ∣ x≥-2且x≠-1}.
3.已知函数f(x+1)的定义域为[-2,3],则f(x-2)的定义域是_________.
解:(3)使根式 成立的实数集合是{x∣-1≤x ≤1},使根式 成立的实数集合是{x ∣x ≧1或x ≤-1}所以此函数的定义域为
{x∣-1≤x ≤1} ∩ {x ∣x ≧1或x ≤-1}={x=1或x=-1}.
[1,6]
4.判断下列函数是否相等,为什么?
两个函数相等当且仅当它们的定义域和对应关系完全一致.与表示自变量和函数值的字母无关.
解:(1)令x+1=y,则这两个函数的对应关系是一样的,并且定义域也是一样的,都是x ∈R,所以这两个函数是相等的.
(2)g (x)=∣x ∣,这两个函数对应关系是一样的,它们的定义域也相同,所以这两个函数相等.
显然这两个函数的定义域都是实数集R,但是当x<0时,它们的对应关系不相同,所以这两个函数的不相等.
3.(1)不相等,因为前者的定义域为{t∣0≤t ≤26},而后者的定义域为R.
(2)不相等,因为前者的定义域为R,而后者的定义域为{x ∣x≠0}.
f :A→B
y=f(x),
1.2.1 函数的概念
远距离航海中对经度与纬度的测量用到函数
1.一枚炮弹发射后,经过26s落到地面击中目标,炮弹的射高为845m,且炮弹距离地面的高度h(单位:m)随时间t(单位:s)变化的规律是
根据问题的实际意义,对于数集A中的任意一个时间t,按照对应关系*,在数集B中都有唯一确定的高度h和它对应.
*
观察实例:
注意:
时间t的变化范围是数集A={t︱0≤t ≤26},
高度h的变化范围是数集B={h ︱0≤h ≤845}.
2.某城市一天各个时刻的温度情况,如图:
对于数集A中的每一个时刻t,都有唯一确定的温度T和它对应.
注意:
时刻t的变化范围是数集A={t︱0≤t ≤24},
温度T的变化范围是数集B={T︱-2 ≤T ≤10}.
3.国际上常用恩格尔系数反映一个国家人民生活水平质量的高低,恩格尔系数越低,生活质量越高。表1中恩格尔系数随时间(年)变化的情况表明,“八五”计划以来,我国城镇居民的生活质量发生了显著变化.
表1“八五”以来中国城镇居民恩格尔系数变化情况
思考表中恩格尔系数与时间(年)的关系?
注意:
时间t的变化范围是数集A={t︱1998≤t ≤2005}
恩格尔系数k的变化范围是数集
B={k︱37.9 ≤k ≤50.1}.
对于数集A中每个年份t,在数集B中都有唯一确定的恩格尔系数与它对应.
以上例子中,变量之间的关系有什么共同的特点呢?
对于集合A中的每个x,按照某种关系f,在数集B中都有唯一确定的y与它对应。
记作:f: A→B.
设A,B是非空的数集,如果按照某种确定的对应关系f,使对集合A中的任意一个数x,在集合B中都有唯一确定的数f(x)和它对应,那么就称f:A→B为从集合A到B的一个函数.记作
y=f(x),x∈A
其中x叫做自变量,x的取值范围A叫做函数的定义域
与x的值相对应的y值叫做函数值,函数值的集合 {f(x)|x∈A} 叫做函数的值域.
知识要点
(1)要求必须是非空集合A,B;
(2)必须是集合A中的任意一个x;
(3)必须是在集合B中有唯一确定的数与之相对应;
(4) “y= f(x)”是函数符号,可以用任意的字母表示,
如“y= g(x)”;
(5)函数符号“y= f(x)”中的 f(x)表示与x对应的函数
值,一个数,而不是f乘x.
注意
下列图像中不能作为函数y=f(x)的图像.
x
y
0
2
-2
x
y
0
2
-2
x
y
0
2
-2
x
y
0
2
-2
×
×
下列函数的定义域,对应关系,值域.
定义域是R,值域是R
对于R中的任意一个数x,在R中都有唯一确定的数y=ax+b(a≠0)和它对应.
思考
定义域是A={ ︱x≠0 },值域是R.
对于集合A中的每一个x,在R中都有唯一确定的值 与它对应.
定义域是R,值域是集合B,当a>0时,B={y︱y≥ },当a<0时,B={y︱y≤ }.
对于R中的任意一个数x,在B中都有唯一确定的
和它对应.
构成函数的三要素是定义域、对应关系和值域.
与函数相关的概念——区间
定义 名称 符号 数轴表示
{x︱a≤x≤b} 闭区间 [a,b]
{x︱a
{x︱a
a
b
a
b
a
b
a
b
用实心点表示包括在区间内的端点,用空心点表示不包括在区间内的点.
集合 符号 数轴表示
R
{x︱x≥a}
{x︱x>a}
{x︱x ≤ b}
{x︱x < b}
a
a
b
b
做一做
(-∞,+ ∞)
[a,+ ∞)
(a,+ ∞ )
(- ∞,b]
(- ∞,b)
(1)区间是集合;
(2)区间的左端点小于右端点;
(3)区间中的元素都是点,可以用数字表示;
(4)任何区间都可以在数轴上表示出来;
(5)以“-∞”,“+∞”为区间的一端时,这一端必须是小括号. 例如(+∞,100]
注意
例1 求下列函数的定义域
分析:函数的定义域通常是由问题的实际背景确定,如果单纯的给出解析式y=f(x),没有指明定义域,那么函数的定义域就是使这个式子有意义的实数的集合.
解:(1)使 有意义,就是 ,即使分数有意义的集合是{x︱x<0},所以这个函数的定义域就是{x︱x<0}.
(2)使根式 有意义的实数的集合是{x︱x≥-2},使分式 成立的实数的集合是{x︱x≠10}.所以,这个函数的定义域就是
{x︱x≥-2} {x︱x≠10}={x︱x ≥-2,且x≠10} .
例2 已知函数
(1)求f(-1),f(0)的值;
(2)当-1≤a ≤ 3时,求f(a)的值.
解:
且边长为正
数,所以0<x<40.
所以面积s=
= (40-x)x (0<x<40)
解: 由题意知,另一边长为
例3 设一个矩形周长为80,其中一边长为x,求它的面积关于x的函数的解析式,并写出定义域.
(1)如果f(x)是整式,那么函数的定义域是实数集R .
(2)如果f(x)是分式,那么函数的定义域是使分母不等于零的实数的集合 .
(3)如果f(x)是二次根式,那么函数的定义域是使根号内的式子大于或等于零的实数的集合.
(4)如果f(x)是由几个部分的数学式子构成的,那么函数定义域是使各部分式子都有意义的实数集合.(即求各集合的交集).
(5)满足实际问题有意义.
几类函数的定义域:
判断两个函数相等:
1 .构成函数三个要素是定义域、对应关系和值域.由于值域是由定义域和对应关系决定的,所以,如果两个函数的定义域和对应关系完全一致,即称这两个函数相等(或为同一函数).
2. 与表示自变量和函数值的字母无关.
知识要点
解: ① f ( x ) = (x -1) 0 =1,其定义域与 g ( x ) = 1的定义域是相同的,所以这两个函数是相等的.
② f ( x ) = x与函数g ( x ) = 的定义域都是实数R,但是当x<0时,它们的对应关系不相同。所以这两个函数不相等.
例4 判断下列函数f(x)与g(x)是否表示同一个函数,说明理由?
① f ( x ) = (x -1) 0;g ( x ) = 1
② f ( x ) = x; g ( x ) =
到现在为止,我们在初中学习的基础上,运用集合和对应的语言刻画了函数的概念,并引进了符号y=f(x),明确了函数的构成要素.通过比较两个函数的定义,你对函数有什么新的认识
这两种定义在实质上是一致的,不同的只是叙述的出发点不同,初中给出的定义是从运动变化的观点出发,而现在所给的定义是从集合、对应的观点出发.
1.函数的概念
设A,B是非空的数集,如果按照某种确定的对应关系f,使对集合A中的任意一个数x,在集合B中都有唯一确定的数f(x)和它对应,那么就称f:A→B为从集合A到B的一个函数.记作
y=f(x),x∈A
其中x叫做自变量,x的取值范围A叫做函数的定义域,与x的值相对应的y值叫做函数值,函数值的集合 {f(x)|x∈A} 叫做函数的值域.
课堂小结
定义 名称 符号 数轴表示
{x︱a≤x≤b} 闭区间 [a,b]
{x︱a
{x︱a
a
b
a
b
a
b
a
b
与函数相关的概念——区间
2.构成函数的三要素
定义域、对应关系和值域.
3.判断两个函数相等
两个函数相等当且仅当它们的定义域和对应关系完全一致,而与表示自变量和函数值的字母无关.
1.已知函数 , 求
课堂练习
解:∵2>1
∴f(2)=-x+1 = -2+1 = -1
f[f(2)]=f(-1)=-1+2=1
2.求下列函数的定义域.
解:(1)使分式有意义的实数集合是
{x∣ 并且x≠1 },所以此函数的定义
域为{x ∣ x≠0且x≠1 } .
( 2 )使根式成立的实数集合是{x∣x≥-2},使分式有意义的实数集合{x∣x≠-1}所以此函数的定义域为{x ∣ x≥-2且x≠-1}.
3.已知函数f(x+1)的定义域为[-2,3],则f(x-2)的定义域是_________.
解:(3)使根式 成立的实数集合是{x∣-1≤x ≤1},使根式 成立的实数集合是{x ∣x ≧1或x ≤-1}所以此函数的定义域为
{x∣-1≤x ≤1} ∩ {x ∣x ≧1或x ≤-1}={x=1或x=-1}.
[1,6]
4.判断下列函数是否相等,为什么?
两个函数相等当且仅当它们的定义域和对应关系完全一致.与表示自变量和函数值的字母无关.
解:(1)令x+1=y,则这两个函数的对应关系是一样的,并且定义域也是一样的,都是x ∈R,所以这两个函数是相等的.
(2)g (x)=∣x ∣,这两个函数对应关系是一样的,它们的定义域也相同,所以这两个函数相等.
显然这两个函数的定义域都是实数集R,但是当x<0时,它们的对应关系不相同,所以这两个函数的不相等.
3.(1)不相等,因为前者的定义域为{t∣0≤t ≤26},而后者的定义域为R.
(2)不相等,因为前者的定义域为R,而后者的定义域为{x ∣x≠0}.
