25.6 相似三角形的应用 同步练习 2021-2022学年冀教版九年级数学上册 (word版含答案)
文档属性
| 名称 | 25.6 相似三角形的应用 同步练习 2021-2022学年冀教版九年级数学上册 (word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 623.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-06 07:30:24 | ||
图片预览




文档简介
2021-2022学年九年级数学上册(冀教版)
25.6相似三角形的应用-同步练习
时间:60分钟
一、单选题
1.如图,是斜靠在墙壁上的长梯,梯脚距离墙角,梯上点距离墙,长,则梯子长为(
)
A.
B.
C.
D.
2.如图,身高为1.5米的某学生想测量一棵大树的高度,他沿着树影由向走,当走到点时,他的影子顶端正好与树的影子顶端重合.此时三点恰好在一条直线上.经测得米,米,则树的高度为(
)
A.3米
B.4米
C.4.5米
D.6米
3.如图,某超市在一楼至二楼之间安装有电梯,天花板与地面平行.张强扛着箱子(人与箱子的总高度约为2.2m)乘电梯刚好安全通过,请你根据图中数据回答,两层楼之间的高度约为(
)
A.5.5m
B.6.2m
C.11m
D.22m
4.如图,AB和CD表示两根直立于地面的柱子,AC和BD表示起固定作用的两根钢筋,AC与BD相交于点M,已知AB=8
m,CD=12m,则点M离地面的高度MH为(
)
A.4
m
B.
C.5m
D.
5.如图是用卡钳测量容器内径的示意图,现量得卡钳上A,D两个端点之间的距离为10m,,则容器的内径是( )
A.5cm
B.10cm
C.15cm
D.20cm
6.为了加强视力保护意识,小明在书房里挂了一张视力表.由于书房空间狭小,他想根据测试距离为的大视力表制作一个测试距离为小视力表.如图,如果大视力表中“”的高度是,那么小视力表中相应“”的高度是(
)
A.
B.
C.
D.
7.“今有邑,东西七里,南北九里,各开中门,出东门一十五里有木,问:出南门几何步而见木?”这段话摘自《九章算术》.意思是说:如图,矩形城池ABCD,东边城墙AB长9里,南边城墙AD长7里,东门点E、南门点F分别是AB、AD中点,EG⊥AB,FH⊥AD,EG=15里,HG经过A点,则FH=(
)
A.1.2
里
B.1.5
里
C.1.05
里
D.1.02
里
8.如图,路灯灯柱OP的长为9米,身高1.8米的小明从距离路灯的底部(点O)20米的点A处,沿AO所在的直线行走14米到点B处时,人影的长度(
)
A.变长了1.5米
B.变短了2.5米
C.变长了3.5米
D.变短了3.5米
二、填空题
9.用杠杆撬石头的示意图如图所示,P是支点,当用力压杠杆的A端时,杠杆绕P点转动,另一端B向上翘起,石头就被撬动.现有一块石头要使其滚动,杠杆的B端必须向上翘起8cm,已知杠杆的动力臂AP与阻力臂BP之比为4:1,要使这块石头滚动,至少要将杠杆的A端向下压_____cm.
10.如图,已知有两堵墙AB,CD,AB墙高2米,两墙之间的距离BC为8米,小明将一架木梯放在距B点3米的E处靠向墙AB时,木梯有很多露出墙外,将木梯绕点E旋转90°靠向墙CD时,木梯刚好达到墙的顶端,则墙CD的高为________米.
11.把一根长为的细铁丝截成两段,每段折为一个等边三角形,已知两个等边三角形高的比为,则它们的边长分别为______和______.
12.如图,光源P在横杆正上方,在灯光下的影子为,,,,点P到的距离是2.7m,则与间的距离是______m.
13.《九章算术》中记载了一种测量井深的方法.如图所示,在井口B处立一根垂直于井口的木杆BD,从木杆的顶端D观察井水水岸C,视线DC与井口的直径AB交于点E,如果测得AB=1.8米,BD=1米,BE=0.2米,那么井深AC为____米.
14.如图所示为某种型号的台灯的横截面图,已知台灯灯柱AB长30cm,且与水平桌面垂直,灯臂AC长为10cm,灯头的横截面△CEF为直角三角形,当灯臂AC与灯柱AB垂直时,沿CE边射出的光线刚好射到底座B点.若不考虑其它因素,则该台灯在桌面可照亮的宽度BD的长为_____cm.
三、解答题
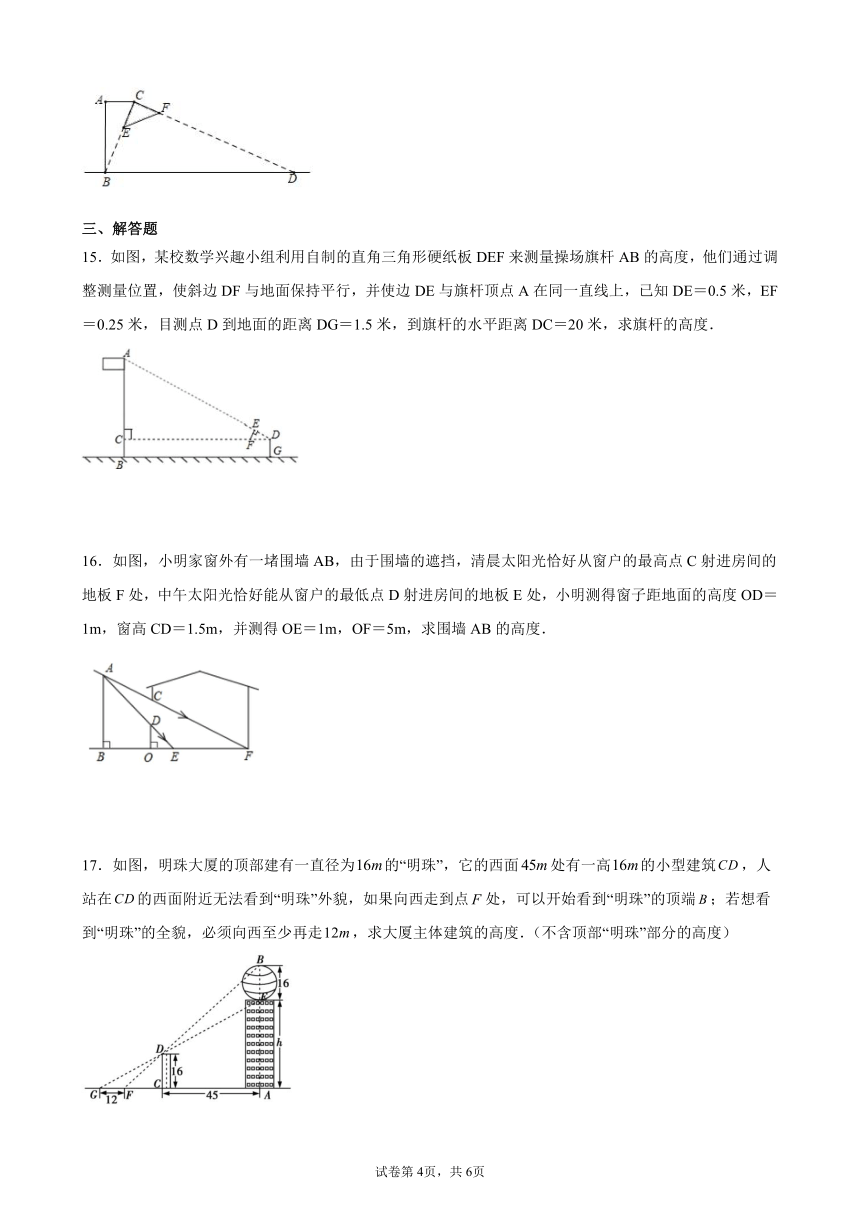
15.如图,某校数学兴趣小组利用自制的直角三角形硬纸板DEF来测量操场旗杆AB的高度,他们通过调整测量位置,使斜边DF与地面保持平行,并使边DE与旗杆顶点A在同一直线上,已知DE=0.5米,EF=0.25米,目测点D到地面的距离DG=1.5米,到旗杆的水平距离DC=20米,求旗杆的高度.
16.如图,小明家窗外有一堵围墙AB,由于围墙的遮挡,清晨太阳光恰好从窗户的最高点C射进房间的地板F处,中午太阳光恰好能从窗户的最低点D射进房间的地板E处,小明测得窗子距地面的高度OD=1m,窗高CD=1.5m,并测得OE=1m,OF=5m,求围墙AB的高度.
17.如图,明珠大厦的顶部建有一直径为的“明珠”,它的西面处有一高的小型建筑,人站在的西面附近无法看到“明珠”外貌,如果向西走到点处,可以开始看到“明珠”的顶端;若想看到“明珠”的全貌,必须向西至少再走,求大厦主体建筑的高度.(不含顶部“明珠”部分的高度)
18.如图,小明同学用自制的直角三角形纸板DEF测量树的高度AB,他调整自己的位置,设法使斜边DF保持水平,并且边DE与点B在同一直线上.已知纸板的两条直角边DE=40cm,EF=20cm,测得边DF离地面的高度AC=1.5m,CD=10m,求树高AB.
19.如图,有一块斜料,,高,将它加工成一个矩形的零件,且此矩形是由两个并排放置的正方形组成,此时这个矩形零件的两边长又分别是多少毫米?
20.王老师要装修自己带阁楼的新居(下图为新居剖面图),在建造客厅到阁楼的楼梯时,为避免上楼时墙角碰头,设计墙角到楼梯的竖直距离为,他量得客厅高,楼梯洞口宽,阁楼阳台宽.请你帮助王老师解决问题:要使墙角到楼梯的竖直距离为,楼梯底端到墙角的距离是多少米?
21.如图,花丛中有一路灯.在灯光下,小明在点D处的影长,沿方向行走到达点G,,这时小明的影长.如果小明的身高为1.7m,求路灯的高度.(精确到0.lm)
22.图1所示的遮阳伞,伞柄垂直于水平地面,其示意图如图2.当伞收紧时,点P与点A重合;当伞慢慢撑开时,动点P由A向B移动;当点P到达点B时,伞张得最开.已知伞在撑开的过程中,总有PM=PN=CM=CN=6.0分米,CE=CF=18.0分米,BC=2.0分米.
﹙1﹚求AP长的取值范围;
﹙2﹚在阳光垂直照射下,伞张得最开时,求伞下的阴影﹙假定为圆面﹚面积S﹙结果保留π﹚.
试卷第2页,共2页
参考答案
1.C
【解析】解:如图,由题意设DE⊥AC于E点,BC⊥AC于C点,
则,,
∵DE⊥AC,BC⊥AC,
∴DE∥BC,
∴△ADE∽△ABC,
∴,
设,
则,
解得:,
经检验,是上述分式方程的解,
∴,
故选:C.
2.D
【解析】解:根据题意,可知:∠ABC=∠EDC=90°,
∵∠C=∠C,
∴△ABC∽△EDC,
∴,即,
∴AB=6.
故选:D.
3.A
【解析】解:如图,过点C作于点F,过点D作,交FC于点E,
易知,
∴,
设,
由题意,得,,
∴,
解得,
∴两层楼之间的高度约为5.5m.
故选A.
4.B
【解析】解:由题意得,AB∥MH∥CD,
∴△CMH∽△CAB,△BMH∽△BDC,
∴,,
∴①+②得,
∴
∵AB=8,CD=12,
∴,
∴,
∴MH=,
故选:B.
5.C
【解析】解:连接AD、BC,
∵,∠AOD=∠BOC,
∴△AOD∽△BOC,
∴,
∵A,D两个端点之间的距离为10m,
∴BC=15m,
故选:C.
6.D
【解析】如图,由题意,得,,.,,,,.故选D.
7.C
【解析】∵EG⊥AB,FH⊥AD,HG经过A点,
∴FA∥EG,EA∥FH,
∴∠HFA=∠AEG=90°,∠FHA=∠EAG,
∴△GEA∽△AFH,
∴=.
∵AB=9里,DA=7里,EG=15里,
∴FA=3.5里,EA=4.5里,
∴=,
解得:FH=1.05里.
故选:C.
8.D
【解析】设小明在A处的影长为x米,B处的影长为y米.
∵AD∥OP,BC∥OP,
∴△ADM∽△OPM,△BCN∽OPN,
∴,,
∵AD=BC,∴,
即,
∴x=5,y=1.5,∴x-y=3.5,故变短了3.5米.故选D.
9.32
【解析】解:如图:AM、BN都与水平线垂直,即AM∥BN;
∴△APM∽△BPN;
∴=,
∵杠杆的动力臂AP与阻力臂BP之比为4:1,
∴=,即AM=4BN;
∴当BN8cm时,AM32cm;
故要使这块石头滚动,至少要将杠杆的端点A向下压32cm.
故答案为:32.
10.7.5
【解析】解:根据题意,得,米,米,米,
∴=5米,
,
,
∴.
∴,
∴,
∴,
∴米.
故答案为:7.5;
11.
【解析】∵所有的等边三角形相似
∴相似比等于这两个等边三角形对应高的比为3:2
∴设它们的周长分别为3xcm,2xcm
∴3x+2x=50
∴x=10
∴它们的周长分别为30cm,20cm
∴它们的边长分别为10cm,
.
故答案为10cm,.
12.1.8
【解析】∵AB∥CD,
∴△PAB∽△PCD,
假设CD到AB距离为x,则
,
又∵AB=2m,CD=6m,
∴,
∴x=1.8m.
故答案为1.8m.
13.7米.
【解析】解:∵BD⊥AB,AC⊥AB,
∴BDAC,
∴△ACE∽△DBE,
∴,
∴,
∴AC=7(米),
故答案为:7(米)
.
14.100cm.
【解析】解:∵AB⊥BD,AC⊥AB,
∴AC∥BD.
∴∠ACB=∠DBC.
∵∠A=∠BCD=90°,
∴△ABC∽△CDB.
∴,
∴BC2=AC BD,
在Rt△ABC中,BC2=AC2+AB2=102+302=1000,
∴10BD=1000.
∴BD=100(cm).
故答案为100.
15.旗杆的高度为11.5m
【解析】解:由题意可得:△DEF∽△DCA,
则,
∵DE=0.5米,EF=0.25米,DG=1.5m,DC=20m,
∴,
解得:AC=10,
故AB=AC+BC=10+1.5=11.5(m).
答:旗杆的高度为11.5m.
16.4m
【解析】解:延长OD,
∵DO⊥BF,
∴∠DOE=90°,
∵OD=1m,OE=1m,
∴∠DEB=45°,
∵AB⊥BF,
∴∠BAE=45°,
∴AB=BE,
设AB=EB=x
m,
∵AB⊥BF,CO⊥BF,
∴AB∥CO,
∴△ABF∽△COF,
∴,
,
解得:x=4.
经检验:x=4是原方程的解.
答:围墙AB的高度是4m.
17.大厦主体建筑的高度为.
【解析】由题图,知,易证,
∴,即,∴.
同理易证,∴,
即,∴.
∵,∴,
解得或(不合题意,舍去).
∴大厦主体建筑的高度为.
18.树高为6.5米.
【解析】解:∵∠DEF=∠BCD=90°∠D=∠D
∴△DEF∽△DCB
∴=
∵DE=40cm=0.4m,EF=20cm=0.2m,AC=1.5m,CD=10m,
∴=
∴BC=5米,
∴AB=AC+BC=1.5+5=6.5米
∴树高为6.5米.
19.,
【解析】解:由题意,设,则,
由题意,得∽,
∴,
∴,
解得:.
∴,
∴矩形的两边长分别是和.
20.1.8
【解析】解:根据题意,有,
∴.
又,
∴∽.
∴.
∴.
解得.
∴.
21.路灯的高度约为6.0m
【解析】由题意,得,,,
∴.∴.
∴.①
同理,,
∴.②
又∵,
∴由①,②可得,
即,
解得.
将代入①,得.
故路灯的高度约为6.0m.
22.(1)AP的取值范围是:0≤x≤10;(2)S最大=315π(平方分米).
【解析】(1)∵BC=2分米,AC=CN+PN=12分米,
∴AB=AC﹣BC=10分米.
∴设AP=x,则AP的取值范围是:0≤x≤10;
(2)连接MN、EF,分别交AC于B、H.
设AP=x分米,
∵PM=PN=CM=CN,
∴四边形PNCM是菱形.
∴MN与PC互相垂直平分,AC是∠ECF的平分线,
PB=
在Rt△MBP中,PM=6分米,
∴MB2=PM2﹣PB2=62﹣(6﹣x)2=6x﹣x2.
∵CE=CF,AC是∠ECF的平分线,
∴EH=HF,EF⊥AC.
∵∠ECH=∠MCB,∠EHC=∠MBC=90°,
∴△CMB∽△CEH.
∴.
∴=()2=
∴EH2=9 MB2=9 (6x﹣x2).
∴S=π EH2=9π(6x﹣x2),
即S=﹣πx2+54πx,
∵x=﹣=12,0≤x≤10,
∴x=10时,S最大=﹣π×100+54π×10=315π(平方分米).
答案第1页,共2页
答案第1页,共2页
25.6相似三角形的应用-同步练习
时间:60分钟
一、单选题
1.如图,是斜靠在墙壁上的长梯,梯脚距离墙角,梯上点距离墙,长,则梯子长为(
)
A.
B.
C.
D.
2.如图,身高为1.5米的某学生想测量一棵大树的高度,他沿着树影由向走,当走到点时,他的影子顶端正好与树的影子顶端重合.此时三点恰好在一条直线上.经测得米,米,则树的高度为(
)
A.3米
B.4米
C.4.5米
D.6米
3.如图,某超市在一楼至二楼之间安装有电梯,天花板与地面平行.张强扛着箱子(人与箱子的总高度约为2.2m)乘电梯刚好安全通过,请你根据图中数据回答,两层楼之间的高度约为(
)
A.5.5m
B.6.2m
C.11m
D.22m
4.如图,AB和CD表示两根直立于地面的柱子,AC和BD表示起固定作用的两根钢筋,AC与BD相交于点M,已知AB=8
m,CD=12m,则点M离地面的高度MH为(
)
A.4
m
B.
C.5m
D.
5.如图是用卡钳测量容器内径的示意图,现量得卡钳上A,D两个端点之间的距离为10m,,则容器的内径是( )
A.5cm
B.10cm
C.15cm
D.20cm
6.为了加强视力保护意识,小明在书房里挂了一张视力表.由于书房空间狭小,他想根据测试距离为的大视力表制作一个测试距离为小视力表.如图,如果大视力表中“”的高度是,那么小视力表中相应“”的高度是(
)
A.
B.
C.
D.
7.“今有邑,东西七里,南北九里,各开中门,出东门一十五里有木,问:出南门几何步而见木?”这段话摘自《九章算术》.意思是说:如图,矩形城池ABCD,东边城墙AB长9里,南边城墙AD长7里,东门点E、南门点F分别是AB、AD中点,EG⊥AB,FH⊥AD,EG=15里,HG经过A点,则FH=(
)
A.1.2
里
B.1.5
里
C.1.05
里
D.1.02
里
8.如图,路灯灯柱OP的长为9米,身高1.8米的小明从距离路灯的底部(点O)20米的点A处,沿AO所在的直线行走14米到点B处时,人影的长度(
)
A.变长了1.5米
B.变短了2.5米
C.变长了3.5米
D.变短了3.5米
二、填空题
9.用杠杆撬石头的示意图如图所示,P是支点,当用力压杠杆的A端时,杠杆绕P点转动,另一端B向上翘起,石头就被撬动.现有一块石头要使其滚动,杠杆的B端必须向上翘起8cm,已知杠杆的动力臂AP与阻力臂BP之比为4:1,要使这块石头滚动,至少要将杠杆的A端向下压_____cm.
10.如图,已知有两堵墙AB,CD,AB墙高2米,两墙之间的距离BC为8米,小明将一架木梯放在距B点3米的E处靠向墙AB时,木梯有很多露出墙外,将木梯绕点E旋转90°靠向墙CD时,木梯刚好达到墙的顶端,则墙CD的高为________米.
11.把一根长为的细铁丝截成两段,每段折为一个等边三角形,已知两个等边三角形高的比为,则它们的边长分别为______和______.
12.如图,光源P在横杆正上方,在灯光下的影子为,,,,点P到的距离是2.7m,则与间的距离是______m.
13.《九章算术》中记载了一种测量井深的方法.如图所示,在井口B处立一根垂直于井口的木杆BD,从木杆的顶端D观察井水水岸C,视线DC与井口的直径AB交于点E,如果测得AB=1.8米,BD=1米,BE=0.2米,那么井深AC为____米.
14.如图所示为某种型号的台灯的横截面图,已知台灯灯柱AB长30cm,且与水平桌面垂直,灯臂AC长为10cm,灯头的横截面△CEF为直角三角形,当灯臂AC与灯柱AB垂直时,沿CE边射出的光线刚好射到底座B点.若不考虑其它因素,则该台灯在桌面可照亮的宽度BD的长为_____cm.
三、解答题
15.如图,某校数学兴趣小组利用自制的直角三角形硬纸板DEF来测量操场旗杆AB的高度,他们通过调整测量位置,使斜边DF与地面保持平行,并使边DE与旗杆顶点A在同一直线上,已知DE=0.5米,EF=0.25米,目测点D到地面的距离DG=1.5米,到旗杆的水平距离DC=20米,求旗杆的高度.
16.如图,小明家窗外有一堵围墙AB,由于围墙的遮挡,清晨太阳光恰好从窗户的最高点C射进房间的地板F处,中午太阳光恰好能从窗户的最低点D射进房间的地板E处,小明测得窗子距地面的高度OD=1m,窗高CD=1.5m,并测得OE=1m,OF=5m,求围墙AB的高度.
17.如图,明珠大厦的顶部建有一直径为的“明珠”,它的西面处有一高的小型建筑,人站在的西面附近无法看到“明珠”外貌,如果向西走到点处,可以开始看到“明珠”的顶端;若想看到“明珠”的全貌,必须向西至少再走,求大厦主体建筑的高度.(不含顶部“明珠”部分的高度)
18.如图,小明同学用自制的直角三角形纸板DEF测量树的高度AB,他调整自己的位置,设法使斜边DF保持水平,并且边DE与点B在同一直线上.已知纸板的两条直角边DE=40cm,EF=20cm,测得边DF离地面的高度AC=1.5m,CD=10m,求树高AB.
19.如图,有一块斜料,,高,将它加工成一个矩形的零件,且此矩形是由两个并排放置的正方形组成,此时这个矩形零件的两边长又分别是多少毫米?
20.王老师要装修自己带阁楼的新居(下图为新居剖面图),在建造客厅到阁楼的楼梯时,为避免上楼时墙角碰头,设计墙角到楼梯的竖直距离为,他量得客厅高,楼梯洞口宽,阁楼阳台宽.请你帮助王老师解决问题:要使墙角到楼梯的竖直距离为,楼梯底端到墙角的距离是多少米?
21.如图,花丛中有一路灯.在灯光下,小明在点D处的影长,沿方向行走到达点G,,这时小明的影长.如果小明的身高为1.7m,求路灯的高度.(精确到0.lm)
22.图1所示的遮阳伞,伞柄垂直于水平地面,其示意图如图2.当伞收紧时,点P与点A重合;当伞慢慢撑开时,动点P由A向B移动;当点P到达点B时,伞张得最开.已知伞在撑开的过程中,总有PM=PN=CM=CN=6.0分米,CE=CF=18.0分米,BC=2.0分米.
﹙1﹚求AP长的取值范围;
﹙2﹚在阳光垂直照射下,伞张得最开时,求伞下的阴影﹙假定为圆面﹚面积S﹙结果保留π﹚.
试卷第2页,共2页
参考答案
1.C
【解析】解:如图,由题意设DE⊥AC于E点,BC⊥AC于C点,
则,,
∵DE⊥AC,BC⊥AC,
∴DE∥BC,
∴△ADE∽△ABC,
∴,
设,
则,
解得:,
经检验,是上述分式方程的解,
∴,
故选:C.
2.D
【解析】解:根据题意,可知:∠ABC=∠EDC=90°,
∵∠C=∠C,
∴△ABC∽△EDC,
∴,即,
∴AB=6.
故选:D.
3.A
【解析】解:如图,过点C作于点F,过点D作,交FC于点E,
易知,
∴,
设,
由题意,得,,
∴,
解得,
∴两层楼之间的高度约为5.5m.
故选A.
4.B
【解析】解:由题意得,AB∥MH∥CD,
∴△CMH∽△CAB,△BMH∽△BDC,
∴,,
∴①+②得,
∴
∵AB=8,CD=12,
∴,
∴,
∴MH=,
故选:B.
5.C
【解析】解:连接AD、BC,
∵,∠AOD=∠BOC,
∴△AOD∽△BOC,
∴,
∵A,D两个端点之间的距离为10m,
∴BC=15m,
故选:C.
6.D
【解析】如图,由题意,得,,.,,,,.故选D.
7.C
【解析】∵EG⊥AB,FH⊥AD,HG经过A点,
∴FA∥EG,EA∥FH,
∴∠HFA=∠AEG=90°,∠FHA=∠EAG,
∴△GEA∽△AFH,
∴=.
∵AB=9里,DA=7里,EG=15里,
∴FA=3.5里,EA=4.5里,
∴=,
解得:FH=1.05里.
故选:C.
8.D
【解析】设小明在A处的影长为x米,B处的影长为y米.
∵AD∥OP,BC∥OP,
∴△ADM∽△OPM,△BCN∽OPN,
∴,,
∵AD=BC,∴,
即,
∴x=5,y=1.5,∴x-y=3.5,故变短了3.5米.故选D.
9.32
【解析】解:如图:AM、BN都与水平线垂直,即AM∥BN;
∴△APM∽△BPN;
∴=,
∵杠杆的动力臂AP与阻力臂BP之比为4:1,
∴=,即AM=4BN;
∴当BN8cm时,AM32cm;
故要使这块石头滚动,至少要将杠杆的端点A向下压32cm.
故答案为:32.
10.7.5
【解析】解:根据题意,得,米,米,米,
∴=5米,
,
,
∴.
∴,
∴,
∴,
∴米.
故答案为:7.5;
11.
【解析】∵所有的等边三角形相似
∴相似比等于这两个等边三角形对应高的比为3:2
∴设它们的周长分别为3xcm,2xcm
∴3x+2x=50
∴x=10
∴它们的周长分别为30cm,20cm
∴它们的边长分别为10cm,
.
故答案为10cm,.
12.1.8
【解析】∵AB∥CD,
∴△PAB∽△PCD,
假设CD到AB距离为x,则
,
又∵AB=2m,CD=6m,
∴,
∴x=1.8m.
故答案为1.8m.
13.7米.
【解析】解:∵BD⊥AB,AC⊥AB,
∴BDAC,
∴△ACE∽△DBE,
∴,
∴,
∴AC=7(米),
故答案为:7(米)
.
14.100cm.
【解析】解:∵AB⊥BD,AC⊥AB,
∴AC∥BD.
∴∠ACB=∠DBC.
∵∠A=∠BCD=90°,
∴△ABC∽△CDB.
∴,
∴BC2=AC BD,
在Rt△ABC中,BC2=AC2+AB2=102+302=1000,
∴10BD=1000.
∴BD=100(cm).
故答案为100.
15.旗杆的高度为11.5m
【解析】解:由题意可得:△DEF∽△DCA,
则,
∵DE=0.5米,EF=0.25米,DG=1.5m,DC=20m,
∴,
解得:AC=10,
故AB=AC+BC=10+1.5=11.5(m).
答:旗杆的高度为11.5m.
16.4m
【解析】解:延长OD,
∵DO⊥BF,
∴∠DOE=90°,
∵OD=1m,OE=1m,
∴∠DEB=45°,
∵AB⊥BF,
∴∠BAE=45°,
∴AB=BE,
设AB=EB=x
m,
∵AB⊥BF,CO⊥BF,
∴AB∥CO,
∴△ABF∽△COF,
∴,
,
解得:x=4.
经检验:x=4是原方程的解.
答:围墙AB的高度是4m.
17.大厦主体建筑的高度为.
【解析】由题图,知,易证,
∴,即,∴.
同理易证,∴,
即,∴.
∵,∴,
解得或(不合题意,舍去).
∴大厦主体建筑的高度为.
18.树高为6.5米.
【解析】解:∵∠DEF=∠BCD=90°∠D=∠D
∴△DEF∽△DCB
∴=
∵DE=40cm=0.4m,EF=20cm=0.2m,AC=1.5m,CD=10m,
∴=
∴BC=5米,
∴AB=AC+BC=1.5+5=6.5米
∴树高为6.5米.
19.,
【解析】解:由题意,设,则,
由题意,得∽,
∴,
∴,
解得:.
∴,
∴矩形的两边长分别是和.
20.1.8
【解析】解:根据题意,有,
∴.
又,
∴∽.
∴.
∴.
解得.
∴.
21.路灯的高度约为6.0m
【解析】由题意,得,,,
∴.∴.
∴.①
同理,,
∴.②
又∵,
∴由①,②可得,
即,
解得.
将代入①,得.
故路灯的高度约为6.0m.
22.(1)AP的取值范围是:0≤x≤10;(2)S最大=315π(平方分米).
【解析】(1)∵BC=2分米,AC=CN+PN=12分米,
∴AB=AC﹣BC=10分米.
∴设AP=x,则AP的取值范围是:0≤x≤10;
(2)连接MN、EF,分别交AC于B、H.
设AP=x分米,
∵PM=PN=CM=CN,
∴四边形PNCM是菱形.
∴MN与PC互相垂直平分,AC是∠ECF的平分线,
PB=
在Rt△MBP中,PM=6分米,
∴MB2=PM2﹣PB2=62﹣(6﹣x)2=6x﹣x2.
∵CE=CF,AC是∠ECF的平分线,
∴EH=HF,EF⊥AC.
∵∠ECH=∠MCB,∠EHC=∠MBC=90°,
∴△CMB∽△CEH.
∴.
∴=()2=
∴EH2=9 MB2=9 (6x﹣x2).
∴S=π EH2=9π(6x﹣x2),
即S=﹣πx2+54πx,
∵x=﹣=12,0≤x≤10,
∴x=10时,S最大=﹣π×100+54π×10=315π(平方分米).
答案第1页,共2页
答案第1页,共2页
同课章节目录
- 第23章 数据分析
- 23.1 平均数与加权平均数
- 23.2 中位数与众数
- 23.3 方差
- 23.4 用样本估计总体
- 第24章 一元二次方程
- 24.1 一元二次方程
- 24.2 解一元二次方程
- 24.3 一元二次方程根与系数的关系
- 24.4 一元二次方程的应用
- 第25章 图形的相似
- 25.1 比例线段
- 25.2 平行线分线段成比例
- 25.3 相似三角形
- 25.4 相似三角形的判定
- 25.5 相似三角形的性质
- 25.6 相似三角形的应用
- 25.7 相似多边形和图形的位似
- 第26章 解直角三角形
- 26.1 锐角三角函数
- 26.2 锐角三角函数的计算
- 26.3 解直角三角形
- 26.4 解直角三角形的应用
- 第27章 反比例函数
- 27.1 反比例函数
- 27.2 反比例函数的图像和性质
- 27.3 反比例函数的应用
- 第28章 圆
- 28.1 圆的概念和性质
- 28.2 过三点的圆
- 28.3 圆心角和圆周角
- 28.4 垂径定理
- 28.5 弧长和扇形面积
