26.4解直角三角形的实际应用-同步练习-2021-2022学年九年级数学上册(冀教版)(word版含答案)
文档属性
| 名称 | 26.4解直角三角形的实际应用-同步练习-2021-2022学年九年级数学上册(冀教版)(word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 797.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-06 07:38:14 | ||
图片预览




文档简介
2021-2022学年九年级数学上册(冀教版)
26.4解直角三角形的实际应用-同步练习
时间:60分钟
一、单选题
1.甲、乙、丙三人放风筝,各人放出的风筝线分别为,线与地平面所成的角分别为,假设风筝线近似看作是拉直的,则所放风筝最高的是(
).
A.甲
B.乙
C.丙
D.无法确定
2.已知两点,若点对点的仰角为,那么对的俯角是(
).
A.
B.
C.
D.
3.如图,为测河两岸相对两抽水泵的距离,在距点的处,测得,则间的距离为(
).
A.
B.
C.
D.
4.为扩大网络信号的辐射范围,某通信公司在一座小山上新建了一座大型的网络信号发射塔.如图,在高为12米的建筑物DE的顶部测得信号发射塔AB顶端的仰角∠FEA=56°,建筑物DE的底部D到山脚底部C的距离DC=16米,小山坡面BC的坡度(或坡比)i=1:0.75,坡长BC=40米(建筑物DE、小山坡BC和网络信号发射塔AB的剖面图在同一平面内,信号发射塔AB与水平线DC垂直),则信号发射塔AB的高约为
( )(参考数据:sin56°≈0.83,cos56°≈0.56,tan56°≈1.48)
A.71.4米
B.59.2米
C.48.2米
D.39.2米
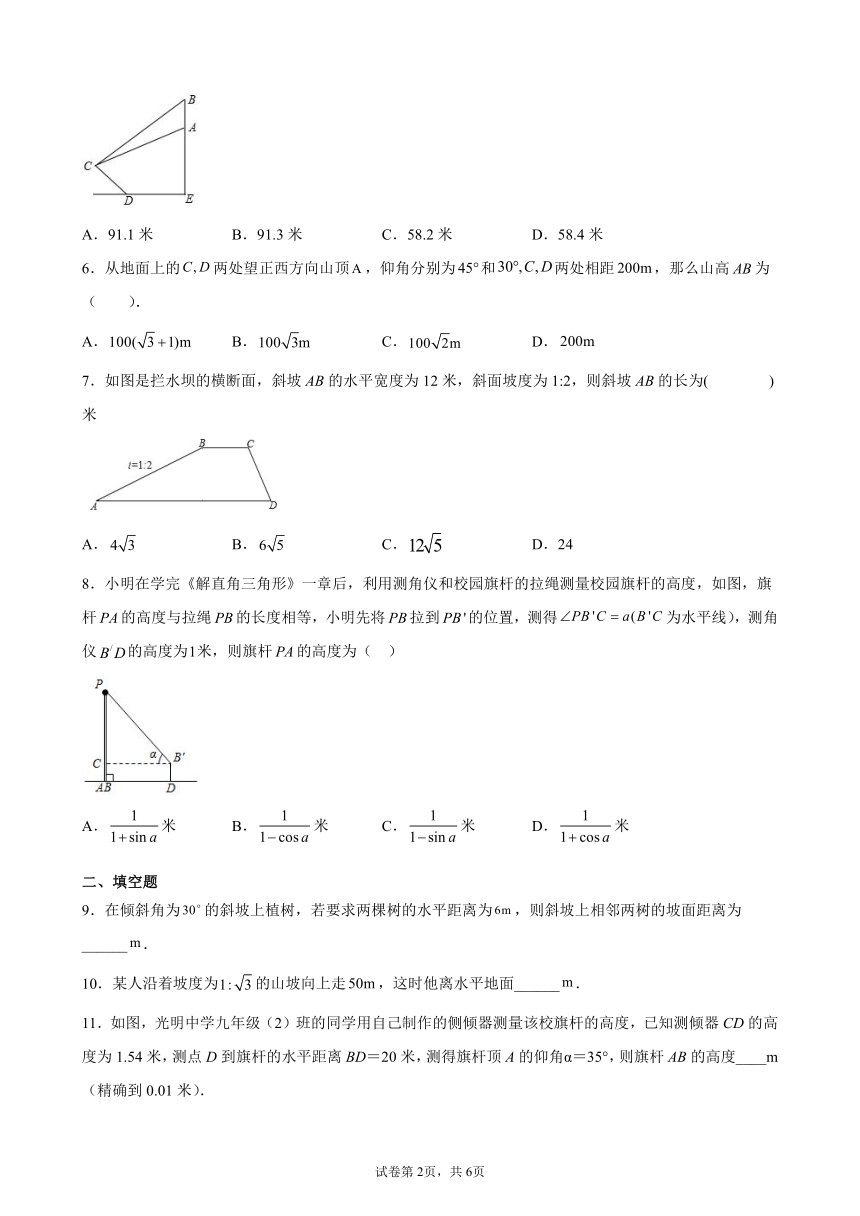
5.如图,某航拍无人机从A点俯拍在坡比为3:4的斜坡上的景点C,此时的俯角为,为取得更震撼的拍摄效果,无人机升高200米到达B点,此时的俯角变为.已知无人机与斜坡的坡底D的水平距离为400米,则斜坡的长度约为(精确到0.1米,参考数据:)(
)
A.91.1米
B.91.3米
C.58.2米
D.58.4米
6.从地面上的两处望正西方向山顶,仰角分别为和两处相距,那么山高为(
).
A.
B.
C.
D.
7.如图是拦水坝的横断面,斜坡AB的水平宽度为12米,斜面坡度为1:2,则斜坡AB的长为(
)米
A.
B.
C.
D.24
8.小明在学完《解直角三角形》一章后,利用测角仪和校园旗杆的拉绳测量校园旗杆的高度,如图,旗杆的高度与拉绳的长度相等,小明先将拉到的位置,测得为水平线),测角仪的高度为米,则旗杆的高度为(
)
A.米
B.米
C.米
D.米
二、填空题
9.在倾斜角为的斜坡上植树,若要求两棵树的水平距离为,则斜坡上相邻两树的坡面距离为______.
10.某人沿着坡度为的山坡向上走,这时他离水平地面______.
11.如图,光明中学九年级(2)班的同学用自己制作的侧倾器测量该校旗杆的高度,已知测倾器CD的高度为1.54米,测点D到旗杆的水平距离BD=20米,测得旗杆顶A的仰角α=35°,则旗杆AB的高度____m(精确到0.01米).
12.如图,已知斜坡长,坡角(即)为,,现计划在斜坡中点D处挖去部分斜坡,修建一个平行于水平线的休闲平台和一条新的斜坡.若修建的斜坡的坡度为3∶1,休闲平台的长是______m.
13.如图,斜坡BE,坡顶B到水平地面的距离AB为3米,坡底AE为16米,在B处,E处分别测得CD顶部点D的仰角为30°,60°,则CD的高度为________米.
14.如图,梯形是拦水坝的横断面图,(图中是指坡面的铅直高度与水平宽度的比),,,,拦水坝的横断面的面积是________(结果保留三位有效数字,参考数据:,)
15.一个长方体木箱沿斜面下滑,当木箱滑至如图位置时,,已知木箱高,斜面坡角为,则木箱端点距地面的高度为_________.
16.如图1所示是放置在水平桌面上的台灯,图2是其侧面示意图,其中底座的示意图为矩形EFGB,EF=2.5cm,,灯罩,灯臂与底座构成的可以绕点C下调节一定的角度.使用发现:当CD平线上方且与水平线所成的角为时,台灯光线最佳,则将台灯调整到光线最佳时点D到桌面FG的距离为________________(参考数据:取1.732,结果精确到0.1cm)
三、解答题
17.如图,为迎接上海2010年世博会,需改变一些老街道的交通状况.在某大道拓宽工程中,要伐掉一棵树,在地面上事先划定以为圆心,半径与等长的圆形区域为危险区,现在某工人站在离点3米处的处测得树的顶端点的仰角为,树的底部点的俯角为,问距离点8米远的保护物是否在危险区内 (取1.73)
18.北京联合张家口成功申办2022年冬奥会后,滑雪运动已成为人们喜爱的娱乐健身项目.如图是某滑雪场为初学者练习用的斜坡示意图,出于安全因素考虑,决定将斜坡的倾角由降为,已知原斜坡坡面长为200米,点在同一水平地面上,求改善后的斜坡坡角向前推进的距离.(结果保留整数.参考数据:
,)
19.某商场为缓解我市“停车难”问题,拟建造地下停车库,如图是该地下停车库坡道入口的设计示意图.其中,AB⊥BD.∠BAD=18°,C在BD上,BC=0.5m.车库坡道入口上方要张贴限高标志.以便告知驾驶员所驾车辆能否安全驶入.为标明限高,请你根据该图计算CE的长度(即点C到AD的距离).(参考数据:sin18°≈0.31,cos18°≈0.95,tan18°≈0.33)(结果精确到0.1m)
20.如图,在同一平面内,两条平行高速公路l1和l2间有一条“Z”型道路连通,其中AB段与高速公路l1成30°角,长为20km;BC段与AB、CD段都垂直,长为10km,CD段长为30km,求两高速公路间的距离(结果保留根号).
21.如图,某乡村学校有教学楼A,在A楼的南偏西45°方向距A楼300米的C处有一辆拖拉机以每秒8米的速度沿北偏东60°的CF方向行驶,若拖拉机的噪声污染半径为100米,试问A教学楼是否受到拖拉机噪声的污染?(计算过程中取1.7,各步计算结果精确到整数)
22.如图,在一条笔直的海岸线上有,两个观测站,在的正东方向.有一艘小船从处沿北偏西方向出发,以每小时20海里速度行驶半小时到达处,从处测得小船在它的北偏东的方向上.
(1)求的距离;
(2)小船沿射线的方向继续航行一段时间后,到达点处,此时,从测得小船在北偏西的方向.求点与点之间的距离.(上述两小题的结果都保留根号)
23.某地的一座人行天桥如图,天桥高为,坡面的坡度为1:1,为了方便行人推车过天桥,有关部门决定降低坡度,使新坡面的坡度为.
(1)求新坡面的坡角;
(2)原天桥底部正前方处(的长)的文化墙是否需要拆除?请说明理由.
试卷第2页,共2页
参考答案
1.B
【解析】解:根据三角函数的定义可以得到,甲、乙、丙三人风筝的高度分别为、、,
,
,
∵
∴所放风筝最高的是乙
故选为B
2.A
【解析】解:如图,
∵A对B的俯角为,
∴B对A的仰角为.
故选A.
3.A
【解析】解:在中,
,
.
又,,
.
故选:.
4.D
【解析】解:如图,延长EF交AB于点H,DC⊥AB于点G,
∵ED⊥DG,
∴四边形EDGH是矩形,
∴GH=ED=12,
∵小山坡面BC的坡度i=1:0.75,即,
设BG=4x,CG=3x,则BC=5x,
∵BC=40,
∴5x=40,
解得x=8,
∴BG=32,CG=24,
∴EH=DG=DC+CG=16+24=40,
BH=BG﹣GH=32﹣12=20,
在Rt△AEH中,∠AEH=56°,
∴AH=EH tan56°≈40×1.48≈59.2,
∴AB=AH﹣BH=59.2﹣20=39.2(米).
答:信号发射塔AB的高约为39.2米.
故选:D.
5.B
【解析】解:如图,过点C作于点P,于点Q,
由题意知,,
设,则,
∵,
∴,
即,解得,
∴,
∵,
∴,
∵斜坡的坡比为:,
∴设,则,
∴,
∴,
∴,
即斜坡的长度约91.3米.
故选B.
6.A
【解析】解:设山高为,
在中,,
∴,
在中,,
∴.
∵,
∴.
解得:.
故选:.
7.B
【解析】解:如图,过B作BE⊥AD于点E,
∵斜面坡度为1:2,AE=12,
∴BE=6,
在Rt△ABC中,
.
故选:B.
8.C
【解析】解:设PA=PB=PB′=x,
在RT△PCB′中,
∴
∴,
∴(1-)x=1,
∴x=.
故选C.
9.
【解析】解:,,
,
米,
米,
故答案为:.
10.
【解析】解:如图所示:
.
.
,
.
故答案为:25.
11.15.54
【解析】解:在Rt△ACE中,∠ACE=α=35°,CE=BD=20,
∴tan∠ACE=,
∴AE=CE tan∠ACE=20 tan35°≈14.004,
∴AB=AE+BE=14.004+1.54≈15.54(米),
故答案为:15.54.
12.20
【解析】解:如图,延长交于点H,
在中,,,
∴,
∵点D为中点,
∴,
又∵,
∴,
∵斜坡的坡度为:,
∴,
∴,即休闲平台的长是.
故答案为:20.
13.
【解析】作BF⊥CD于点F,设DF=x米,
在Rt△DBF中,tan∠DBF=,则BF=,
在Rt△DCE中,DC=x+CF=x+AB=3+x,
在Rt△DCE中,tan∠DEC=,则EC=.
由BF CE=AE,得x =16
解得:x=,
则CD=+3=()米.
故答案为:.
14.52.0
【解析】解:如图,过点A作于点F,
,
,
,
∵,
∴,
∵,
,
,
∴.
故答案是:52.0.
15.3
【解析】解:连接AE,在Rt△ABE中,已知AB=3m,BE=,
∴根据勾股定理得.
又∵,∴.
在Rt△AEF中,,
∴.
故答案为:3.
16.52.1
【解析】解:如图,作CM⊥AB于M,DH⊥AB于点H,交FG于N,CF⊥DH于F,
∵∠CMH=∠CFH=∠FHM=90°,
∴四边形CMHF是矩形,
∴CM=FH,
在Rt△AMC中,
∵AC=40cm,∠CAB=60°,
∴CM=AC sin60°≈34.64(cm),
∴FH=CM=34.6(cm),
∵CD=30cm,∠DCF=30°,
∴DF=(cm),
∵四边形EFGH为矩形,∠EHN=90°,
∴四边形EFNH是矩形,
∴EF=HN=2.5cm,
∴DN=DF+FH+HN=15+34.6+2.5=52.1(cm);
故答案为:52.1.
17.不在危险区内
【解析】解:过点作,如下图
由题意可知四边形为矩形,则
在中,,,
解得
在中,,,
解得
则
答:距离点8米远的保护物不在危险区内
18.104米
【解析】解:,,,
∴在中,,
米,
∵在中,,
米,
米,
答:改善后的斜坡坡角向前推进的距离为104米.
19.2.3米
【解析】解:在Rt△ABD中,∠ABD=90°,∠BAD=18°,AB=9,
∴BD=tan18°×AB≈0.33×9=2.97米,
∵∠DCE+∠ADB=90°,∠BAD+∠ADB=90°,
∴∠DCE=∠BAD=18°,
在Rt△CDE中,∠CED=90°,∠DCE=18°,CD=BD﹣BC=2.97﹣0.5=2.47(米),
∴CE=cos18°×CD≈0.95×2.47≈2.3(米).
20.km
【解析】过B点作BE⊥l1,交l1于E,CD于F,l2于G.
在Rt△ABE中,BE=AB sin30°=20×=10km,
在Rt△BCF中,BF=BC÷cos30°=10÷km,
CF=BF sin30°=km,
DF=CD﹣CF=(30﹣)km,
在Rt△DFG中,FG=DF sin30°=(30﹣)×=(15﹣)km,
∴EG=BE+BF+FG=(25+5)km.
故两高速公路间的距离为(25+5)km.
21.A教室不受影响
【解析】解:过点A作AE⊥CF于点E,将C沿水平方向延长至L,过点A作
AD
⊥CL于点D,
∴在直角三角形ACD中,∠CAD=45°,
AC=300,
∴sin∠CAD=,
∴CD=AD=300,
在直角三角形MCD中,∠MCD=30°,CD=300,
∴
tan∠MCD=,
∴
MD=100,
∴AM=AD-MD=300-100,
∵∠AME=∠CMD=60°,
在直角三角形AME中,AM=300-100,
∴
sin∠AME=,
∴AE=150×(-1)
≈110(米)
,
∵110>100,
∴A教室不受拖拉机噪声的污染.
22.(1)海里;(2)海里.
【解析】解:(1)如图,过点作于点,
在中,,,
∵,
∴
在中,,,
∴.
∴海里
(2)如图,过点作于点,
在中,,,
∴
在中,.
在中,,,
∴海里.
∴点与点之间的距离为海里.
23.(1)新坡面的坡角为;(2)文化墙不需要拆除.理由见解析.
【解析】解:(1)∵新坡面的坡度为,
∴,
∴.
即新坡面的坡角为;
(2)文化墙不需要拆除.
理由:如图,过点C作于点D,则,
∵坡面的坡度为1∶1,新坡面的坡度为,
∴,,
∴,
∴文化墙不需要拆除.
答案第1页,共2页
答案第1页,共2页
26.4解直角三角形的实际应用-同步练习
时间:60分钟
一、单选题
1.甲、乙、丙三人放风筝,各人放出的风筝线分别为,线与地平面所成的角分别为,假设风筝线近似看作是拉直的,则所放风筝最高的是(
).
A.甲
B.乙
C.丙
D.无法确定
2.已知两点,若点对点的仰角为,那么对的俯角是(
).
A.
B.
C.
D.
3.如图,为测河两岸相对两抽水泵的距离,在距点的处,测得,则间的距离为(
).
A.
B.
C.
D.
4.为扩大网络信号的辐射范围,某通信公司在一座小山上新建了一座大型的网络信号发射塔.如图,在高为12米的建筑物DE的顶部测得信号发射塔AB顶端的仰角∠FEA=56°,建筑物DE的底部D到山脚底部C的距离DC=16米,小山坡面BC的坡度(或坡比)i=1:0.75,坡长BC=40米(建筑物DE、小山坡BC和网络信号发射塔AB的剖面图在同一平面内,信号发射塔AB与水平线DC垂直),则信号发射塔AB的高约为
( )(参考数据:sin56°≈0.83,cos56°≈0.56,tan56°≈1.48)
A.71.4米
B.59.2米
C.48.2米
D.39.2米
5.如图,某航拍无人机从A点俯拍在坡比为3:4的斜坡上的景点C,此时的俯角为,为取得更震撼的拍摄效果,无人机升高200米到达B点,此时的俯角变为.已知无人机与斜坡的坡底D的水平距离为400米,则斜坡的长度约为(精确到0.1米,参考数据:)(
)
A.91.1米
B.91.3米
C.58.2米
D.58.4米
6.从地面上的两处望正西方向山顶,仰角分别为和两处相距,那么山高为(
).
A.
B.
C.
D.
7.如图是拦水坝的横断面,斜坡AB的水平宽度为12米,斜面坡度为1:2,则斜坡AB的长为(
)米
A.
B.
C.
D.24
8.小明在学完《解直角三角形》一章后,利用测角仪和校园旗杆的拉绳测量校园旗杆的高度,如图,旗杆的高度与拉绳的长度相等,小明先将拉到的位置,测得为水平线),测角仪的高度为米,则旗杆的高度为(
)
A.米
B.米
C.米
D.米
二、填空题
9.在倾斜角为的斜坡上植树,若要求两棵树的水平距离为,则斜坡上相邻两树的坡面距离为______.
10.某人沿着坡度为的山坡向上走,这时他离水平地面______.
11.如图,光明中学九年级(2)班的同学用自己制作的侧倾器测量该校旗杆的高度,已知测倾器CD的高度为1.54米,测点D到旗杆的水平距离BD=20米,测得旗杆顶A的仰角α=35°,则旗杆AB的高度____m(精确到0.01米).
12.如图,已知斜坡长,坡角(即)为,,现计划在斜坡中点D处挖去部分斜坡,修建一个平行于水平线的休闲平台和一条新的斜坡.若修建的斜坡的坡度为3∶1,休闲平台的长是______m.
13.如图,斜坡BE,坡顶B到水平地面的距离AB为3米,坡底AE为16米,在B处,E处分别测得CD顶部点D的仰角为30°,60°,则CD的高度为________米.
14.如图,梯形是拦水坝的横断面图,(图中是指坡面的铅直高度与水平宽度的比),,,,拦水坝的横断面的面积是________(结果保留三位有效数字,参考数据:,)
15.一个长方体木箱沿斜面下滑,当木箱滑至如图位置时,,已知木箱高,斜面坡角为,则木箱端点距地面的高度为_________.
16.如图1所示是放置在水平桌面上的台灯,图2是其侧面示意图,其中底座的示意图为矩形EFGB,EF=2.5cm,,灯罩,灯臂与底座构成的可以绕点C下调节一定的角度.使用发现:当CD平线上方且与水平线所成的角为时,台灯光线最佳,则将台灯调整到光线最佳时点D到桌面FG的距离为________________(参考数据:取1.732,结果精确到0.1cm)
三、解答题
17.如图,为迎接上海2010年世博会,需改变一些老街道的交通状况.在某大道拓宽工程中,要伐掉一棵树,在地面上事先划定以为圆心,半径与等长的圆形区域为危险区,现在某工人站在离点3米处的处测得树的顶端点的仰角为,树的底部点的俯角为,问距离点8米远的保护物是否在危险区内 (取1.73)
18.北京联合张家口成功申办2022年冬奥会后,滑雪运动已成为人们喜爱的娱乐健身项目.如图是某滑雪场为初学者练习用的斜坡示意图,出于安全因素考虑,决定将斜坡的倾角由降为,已知原斜坡坡面长为200米,点在同一水平地面上,求改善后的斜坡坡角向前推进的距离.(结果保留整数.参考数据:
,)
19.某商场为缓解我市“停车难”问题,拟建造地下停车库,如图是该地下停车库坡道入口的设计示意图.其中,AB⊥BD.∠BAD=18°,C在BD上,BC=0.5m.车库坡道入口上方要张贴限高标志.以便告知驾驶员所驾车辆能否安全驶入.为标明限高,请你根据该图计算CE的长度(即点C到AD的距离).(参考数据:sin18°≈0.31,cos18°≈0.95,tan18°≈0.33)(结果精确到0.1m)
20.如图,在同一平面内,两条平行高速公路l1和l2间有一条“Z”型道路连通,其中AB段与高速公路l1成30°角,长为20km;BC段与AB、CD段都垂直,长为10km,CD段长为30km,求两高速公路间的距离(结果保留根号).
21.如图,某乡村学校有教学楼A,在A楼的南偏西45°方向距A楼300米的C处有一辆拖拉机以每秒8米的速度沿北偏东60°的CF方向行驶,若拖拉机的噪声污染半径为100米,试问A教学楼是否受到拖拉机噪声的污染?(计算过程中取1.7,各步计算结果精确到整数)
22.如图,在一条笔直的海岸线上有,两个观测站,在的正东方向.有一艘小船从处沿北偏西方向出发,以每小时20海里速度行驶半小时到达处,从处测得小船在它的北偏东的方向上.
(1)求的距离;
(2)小船沿射线的方向继续航行一段时间后,到达点处,此时,从测得小船在北偏西的方向.求点与点之间的距离.(上述两小题的结果都保留根号)
23.某地的一座人行天桥如图,天桥高为,坡面的坡度为1:1,为了方便行人推车过天桥,有关部门决定降低坡度,使新坡面的坡度为.
(1)求新坡面的坡角;
(2)原天桥底部正前方处(的长)的文化墙是否需要拆除?请说明理由.
试卷第2页,共2页
参考答案
1.B
【解析】解:根据三角函数的定义可以得到,甲、乙、丙三人风筝的高度分别为、、,
,
,
∵
∴所放风筝最高的是乙
故选为B
2.A
【解析】解:如图,
∵A对B的俯角为,
∴B对A的仰角为.
故选A.
3.A
【解析】解:在中,
,
.
又,,
.
故选:.
4.D
【解析】解:如图,延长EF交AB于点H,DC⊥AB于点G,
∵ED⊥DG,
∴四边形EDGH是矩形,
∴GH=ED=12,
∵小山坡面BC的坡度i=1:0.75,即,
设BG=4x,CG=3x,则BC=5x,
∵BC=40,
∴5x=40,
解得x=8,
∴BG=32,CG=24,
∴EH=DG=DC+CG=16+24=40,
BH=BG﹣GH=32﹣12=20,
在Rt△AEH中,∠AEH=56°,
∴AH=EH tan56°≈40×1.48≈59.2,
∴AB=AH﹣BH=59.2﹣20=39.2(米).
答:信号发射塔AB的高约为39.2米.
故选:D.
5.B
【解析】解:如图,过点C作于点P,于点Q,
由题意知,,
设,则,
∵,
∴,
即,解得,
∴,
∵,
∴,
∵斜坡的坡比为:,
∴设,则,
∴,
∴,
∴,
即斜坡的长度约91.3米.
故选B.
6.A
【解析】解:设山高为,
在中,,
∴,
在中,,
∴.
∵,
∴.
解得:.
故选:.
7.B
【解析】解:如图,过B作BE⊥AD于点E,
∵斜面坡度为1:2,AE=12,
∴BE=6,
在Rt△ABC中,
.
故选:B.
8.C
【解析】解:设PA=PB=PB′=x,
在RT△PCB′中,
∴
∴,
∴(1-)x=1,
∴x=.
故选C.
9.
【解析】解:,,
,
米,
米,
故答案为:.
10.
【解析】解:如图所示:
.
.
,
.
故答案为:25.
11.15.54
【解析】解:在Rt△ACE中,∠ACE=α=35°,CE=BD=20,
∴tan∠ACE=,
∴AE=CE tan∠ACE=20 tan35°≈14.004,
∴AB=AE+BE=14.004+1.54≈15.54(米),
故答案为:15.54.
12.20
【解析】解:如图,延长交于点H,
在中,,,
∴,
∵点D为中点,
∴,
又∵,
∴,
∵斜坡的坡度为:,
∴,
∴,即休闲平台的长是.
故答案为:20.
13.
【解析】作BF⊥CD于点F,设DF=x米,
在Rt△DBF中,tan∠DBF=,则BF=,
在Rt△DCE中,DC=x+CF=x+AB=3+x,
在Rt△DCE中,tan∠DEC=,则EC=.
由BF CE=AE,得x =16
解得:x=,
则CD=+3=()米.
故答案为:.
14.52.0
【解析】解:如图,过点A作于点F,
,
,
,
∵,
∴,
∵,
,
,
∴.
故答案是:52.0.
15.3
【解析】解:连接AE,在Rt△ABE中,已知AB=3m,BE=,
∴根据勾股定理得.
又∵,∴.
在Rt△AEF中,,
∴.
故答案为:3.
16.52.1
【解析】解:如图,作CM⊥AB于M,DH⊥AB于点H,交FG于N,CF⊥DH于F,
∵∠CMH=∠CFH=∠FHM=90°,
∴四边形CMHF是矩形,
∴CM=FH,
在Rt△AMC中,
∵AC=40cm,∠CAB=60°,
∴CM=AC sin60°≈34.64(cm),
∴FH=CM=34.6(cm),
∵CD=30cm,∠DCF=30°,
∴DF=(cm),
∵四边形EFGH为矩形,∠EHN=90°,
∴四边形EFNH是矩形,
∴EF=HN=2.5cm,
∴DN=DF+FH+HN=15+34.6+2.5=52.1(cm);
故答案为:52.1.
17.不在危险区内
【解析】解:过点作,如下图
由题意可知四边形为矩形,则
在中,,,
解得
在中,,,
解得
则
答:距离点8米远的保护物不在危险区内
18.104米
【解析】解:,,,
∴在中,,
米,
∵在中,,
米,
米,
答:改善后的斜坡坡角向前推进的距离为104米.
19.2.3米
【解析】解:在Rt△ABD中,∠ABD=90°,∠BAD=18°,AB=9,
∴BD=tan18°×AB≈0.33×9=2.97米,
∵∠DCE+∠ADB=90°,∠BAD+∠ADB=90°,
∴∠DCE=∠BAD=18°,
在Rt△CDE中,∠CED=90°,∠DCE=18°,CD=BD﹣BC=2.97﹣0.5=2.47(米),
∴CE=cos18°×CD≈0.95×2.47≈2.3(米).
20.km
【解析】过B点作BE⊥l1,交l1于E,CD于F,l2于G.
在Rt△ABE中,BE=AB sin30°=20×=10km,
在Rt△BCF中,BF=BC÷cos30°=10÷km,
CF=BF sin30°=km,
DF=CD﹣CF=(30﹣)km,
在Rt△DFG中,FG=DF sin30°=(30﹣)×=(15﹣)km,
∴EG=BE+BF+FG=(25+5)km.
故两高速公路间的距离为(25+5)km.
21.A教室不受影响
【解析】解:过点A作AE⊥CF于点E,将C沿水平方向延长至L,过点A作
AD
⊥CL于点D,
∴在直角三角形ACD中,∠CAD=45°,
AC=300,
∴sin∠CAD=,
∴CD=AD=300,
在直角三角形MCD中,∠MCD=30°,CD=300,
∴
tan∠MCD=,
∴
MD=100,
∴AM=AD-MD=300-100,
∵∠AME=∠CMD=60°,
在直角三角形AME中,AM=300-100,
∴
sin∠AME=,
∴AE=150×(-1)
≈110(米)
,
∵110>100,
∴A教室不受拖拉机噪声的污染.
22.(1)海里;(2)海里.
【解析】解:(1)如图,过点作于点,
在中,,,
∵,
∴
在中,,,
∴.
∴海里
(2)如图,过点作于点,
在中,,,
∴
在中,.
在中,,,
∴海里.
∴点与点之间的距离为海里.
23.(1)新坡面的坡角为;(2)文化墙不需要拆除.理由见解析.
【解析】解:(1)∵新坡面的坡度为,
∴,
∴.
即新坡面的坡角为;
(2)文化墙不需要拆除.
理由:如图,过点C作于点D,则,
∵坡面的坡度为1∶1,新坡面的坡度为,
∴,,
∴,
∴文化墙不需要拆除.
答案第1页,共2页
答案第1页,共2页
同课章节目录
- 第23章 数据分析
- 23.1 平均数与加权平均数
- 23.2 中位数与众数
- 23.3 方差
- 23.4 用样本估计总体
- 第24章 一元二次方程
- 24.1 一元二次方程
- 24.2 解一元二次方程
- 24.3 一元二次方程根与系数的关系
- 24.4 一元二次方程的应用
- 第25章 图形的相似
- 25.1 比例线段
- 25.2 平行线分线段成比例
- 25.3 相似三角形
- 25.4 相似三角形的判定
- 25.5 相似三角形的性质
- 25.6 相似三角形的应用
- 25.7 相似多边形和图形的位似
- 第26章 解直角三角形
- 26.1 锐角三角函数
- 26.2 锐角三角函数的计算
- 26.3 解直角三角形
- 26.4 解直角三角形的应用
- 第27章 反比例函数
- 27.1 反比例函数
- 27.2 反比例函数的图像和性质
- 27.3 反比例函数的应用
- 第28章 圆
- 28.1 圆的概念和性质
- 28.2 过三点的圆
- 28.3 圆心角和圆周角
- 28.4 垂径定理
- 28.5 弧长和扇形面积
