25.7相似多边形和图形的位似-同步练习-2021-2022学年九年级数学上册(冀教版)(word版含答案)
文档属性
| 名称 | 25.7相似多边形和图形的位似-同步练习-2021-2022学年九年级数学上册(冀教版)(word版含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 526.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-06 00:00:00 | ||
图片预览

文档简介
2021-2022学年九年级数学上册(冀教版)
25.7相似多边形和图形的位似-同步练习
时间:60分钟
一、单选题
1.观察下列四组图形,不相似的一组图形是(
)
A.
B.
C.
D.
2.如图,四边形与四边形是位似图形,则位似中心是(
)
A.点
B.点
C.点
D.点
3.如图,两个四边形是位似图形,则它们的位似中心是(
)
A.点M
B.点N
C.点O
D.点P
4.下列图形中一定相似的一组是(
).
A.邻边对应成比例的两个平行四边形
B.有一条边相等的两个矩形
C.有一条边相等的两个菱形
D.底角都是的两个等腰三角形
5.若某个直角三角形的两直角边之比为,则确定了该三角形的(
)
A.形状
B.周长
C.面积
D.斜边
6.将以点为位似中心放大为原来的倍,得到,则等于(
)
A.
B.
C.
D.
7.下列相似图形不是位似图形的是(
)
A.
B.
C.
D.
8.如图所示的四边形,与选项中的四边形一定相似的是( )
A.
B.
C.
D.
二、填空题
9.如图所示的两个五边形相似,则_____,______,_______,______.
10.如图,用放大镜将图形放大,应属于哪一种变换:_________(请选填:对称变换、平移变换、旋转变换、相似变换).
11.把△ABC三点坐标A(0,1)、B(2,0)、C(3,2)分别乘以3得△A'B'C',的坐标A',(0,3)、B'(6,0)、C(9,6),那么△ABC与△A'B'C'是______图形,位似中心是_______,相似比为________
12.如图,已知与是相似比为的位似图形,点O为位似中心,若内一点与内一点是一对对应点,则点的坐标是______.
13.如图,△OAB与△OCD是以点O为位似中心的位似图形,相似比为3∶4,∠OCD=90°,∠AOB=60°,若点B的坐标是(6,0),则点C的坐标是______.
14.一个四边形的边长分别是3,4,5,6,另一个与它形状相同的四边形最小边长为6,则另一个四边形的周长是________.
15.如图,矩形的两边在坐标轴上,点为平面直角坐标系的原点,以轴上的某一点为位似中心,作位似图形,且点的坐标,则位似中心的坐标为__________.
16.如图,△ABC与△DEF位似,位似中心为点O,且BC:EF=3:2,则S△ABC:S△DEF=_____.
三、解答题
17.观察图中①~⑩的图形,其中哪些图形分别与(1),(2),(3),(4)相似?
(1)
(2)
(3)
(4)
①
②
③
④
⑤
⑥
⑦
⑧
⑨
⑩
18.如图,所示的两个矩形是否相似?并简单说明理由.
19.画图:点,把以点为位似中心放大到原来的倍,且写出对应顶点的坐标.
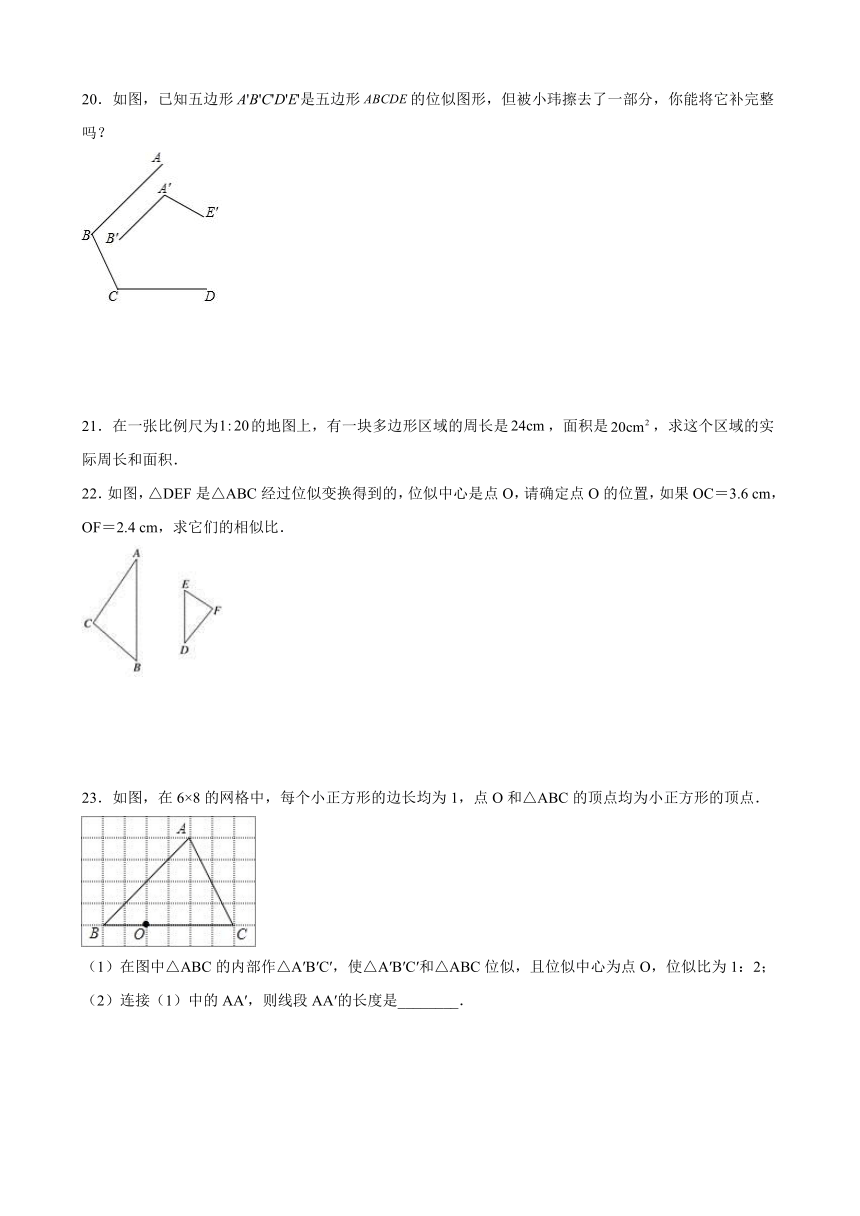
20.如图,已知五边形A'B'C'D'E'是五边形的位似图形,但被小玮擦去了一部分,你能将它补完整吗?
21.在一张比例尺为的地图上,有一块多边形区域的周长是,面积是,求这个区域的实际周长和面积.
22.如图,△DEF是△ABC经过位似变换得到的,位似中心是点O,请确定点O的位置,如果OC=3.6
cm,OF=2.4
cm,求它们的相似比.
23.如图,在6×8的网格中,每个小正方形的边长均为1,点O和△ABC的顶点均为小正方形的顶点.
(1)在图中△ABC的内部作△A′B′C′,使△A′B′C′和△ABC位似,且位似中心为点O,位似比为1:2;
(2)连接(1)中的AA′,则线段AA′的长度是________.
24.如图,是由经过位似变换得到的
(1)求出与的相似比,并指出它们的位似中心;
(2)是的位似图形吗?如果是,求相似比;如果不是说明理由;
(3)如果相似比为,那么的位似图形是什么?
试卷第2页,共2页
参考答案
1.C
【解析】解:大小不同,形状相同,所以是相似图形,故A选项错误;
大小不同,形状相同,所以是相似图形,故B选项错误;
大小不同,形状不相同,所以不是相似图形,故C选项正确;
大小不同,形状相同,所以是相似图形,故D选项错误.
故选:C.
2.B
【解析】解:由图可知,对应边AG与CE的延长线交于点B,
∴点B为位似中心
故选B.
3.D
【解析】解:如图,位似中心是点P.
故选D
4.D
【解析】解:A、邻边对应成比例的两个平行四边形,对应的角不一定相等,因而不一定相似,故错误,不符合题意;
B、有一条边相等的两个矩形,对应边的比不一定相等,因而不一定相似,故错误,不符合题意;;
C、有一个内角对应相等的两个平行四边形,对应边的比不一定相等,故错误,不符合题意;;
D、底角都是60°的等腰三角形一定是等边三角形,因而一定相似,故正确,符合题意;.
故选:D.
5.A
【解析】解:∵直角三角形的两直角边之比为2:3,
∴虽不能确定两直角边的值,但能确定其比值,
∴能确定该直角三角形的形状,
故选:A.
6.C
【解析】∵
将以点为位似中心放大为原来的倍,得到,
∴
与的位似比为,
则=.
故选:C
7.D
【解析】解:D中两个图形,对应边不互相平行,不是位似图形,
A、B、C中的图形符合位似变换的定义,是位似图形,
故选:D.
8.D
【解析】作AE⊥BC于E,
则四边形AECD为矩形,
∴EC=AD=1,AE=CD=3,
∴BE=4,
由勾股定理得,AB==5,
∴四边形ABCD的四条边之比为1:3:5:5,
D选项中,四条边之比为1:3:5:5,且对应角相等,
故选:D.
9.3
4.5
4
6
【解析】解:∵两个五边形相似,
∴,,,,
解得,a=3,b=4.5,c=4,d=6.
10.相似变换
【解析】由一个图形到另一个图形,在改变的过程中形状不变,大小产生变化,属于相似变化.
故答案为相似变换.
11.位似
原点O
3
【解析】
根据题意在平面直角坐标系中可以画出图形,可得:
△ABC与△A'B'C'是位似图形,位似中心是原点O,相似比为3.
故答案为:位似;
原点O;
3.
12.
【解析】∵P(x,y),相似比为1:2,点O为位似中心,
∴P′的坐标是( 2x, 2y).故答案为( 2x, 2y).
13.(2,2)
【解析】分别过A、C作AE⊥OB,CF⊥OB,
∵∠OCD=90°,∠AOB=60°,
∴∠ABO=∠CDO=30°,∠OCF=30°,
∵△OAB与△OCD是以点O为位似中心的位似图形,相似比为3:4,点B的坐标是(6,0),
∴D(8,0),则DO=8,
故OC=4,
则FO=2,CF=CO cos30°=4×=2,
故点C的坐标是:(2,2).
故答案为:(2,2).
14.36
【解析】根据对应边成比例,得出该四边形的另三条边的长分别是8,10,12.所以周长为6+8+10+12=36.
15.
【解析】解:如图所示,连接BF交y轴于P,
∵四边形ABCD和四边形EFGO是矩形,点B,F的坐标分别为( 4,4),(2,1),
∴点C的坐标为(0,4),点G的坐标为(0,1),
∴CG=3,
∵BC∥GF,
∴△PGF∽△PCB,
∴GP:PC=GF:BC=1:2,
∴GP=1,PC=2,
∴OP=2,
∴点P的坐标为(0,2),
即:位似中心的坐标为(0,2).
故答案为(0,2).
16.9:4
【解析】解:∵△ABC与△DEF位似,
∴△ABC∽△DEF,
∵BC:EF=3:2,
∴
,
故答案为:9:4.
17.与(1)相似的图形是⑦;与(2)相似的图形是①⑧;与(3)相似的图形是②④;与(4)相似的图形是⑩.
【解析】解:与(1)相似的图形是⑦;
与(2)相似的图形是①⑧;
与(3)相似的图形是②④;
与(4)相似的图形是⑩.
18.相似,见解析
【解析】解:相似.
理由:这两个的角是直角,因而对应角相等一定是正确的,
小矩形的长是20-5-5=10,宽是12-3-3=6,
因为,即两个矩形的对应边的比相等,
因而这两个矩形相似.
19.作图见解析,,,或,,.
【解析】解:延长到,使,得到点的对应点,
同法得到点的对应点,点的对应点不变,连接,
就是所求的三角形;
或反向延长或,由同样的方法得到的对应点
连接就是所求的三角形;
由,
,,.
或,,.
20.补充图形见解析
【解析】解:如图,分别延长AA′、BB′,它们相交于点O,再过点A作AE∥A′E′交OE′的延长线于E,过点B′作B′C′∥BC′交OC于C′,过点C′作C′D′∥CD交OD于D′,然后连接DE、D′E′即可.
21.周长480cm,面积8000
cm2
【解析】设实际周长是,则:
,
解得:();
面积之比等于相似比的平方,设实际面积是平方厘米,则:
,
解得:()
.
22.3∶2.
【解析】解:连接AD,CF交于点O,
则点O即为所求;
∵OC=3.6
cm,OF=2.4
cm,
∴OC:OF=3∶2,
∴△ABC与△DEF的相似比为3∶2.
23.(1)作图见解析;(2).
【解析】(1)如下图,△A′B′C′为所作;
(2)由图结合勾股定理可得:AO=,
∵点OA′:OA=1:2,
∴OA′=OA=,
∴AA′=OA-OA′=.
24.;它们的位似中心是;(2)是的位似图形,相似比为;(3)如果相似比为,那么的位似图形是.
【解析】与的相似比为:;它们的位似中心是;
(2)是的位似图形,
相似比为:;
(3)如果相似比为,那么的位似图形是.
答案第1页,共2页
答案第1页,共2页
25.7相似多边形和图形的位似-同步练习
时间:60分钟
一、单选题
1.观察下列四组图形,不相似的一组图形是(
)
A.
B.
C.
D.
2.如图,四边形与四边形是位似图形,则位似中心是(
)
A.点
B.点
C.点
D.点
3.如图,两个四边形是位似图形,则它们的位似中心是(
)
A.点M
B.点N
C.点O
D.点P
4.下列图形中一定相似的一组是(
).
A.邻边对应成比例的两个平行四边形
B.有一条边相等的两个矩形
C.有一条边相等的两个菱形
D.底角都是的两个等腰三角形
5.若某个直角三角形的两直角边之比为,则确定了该三角形的(
)
A.形状
B.周长
C.面积
D.斜边
6.将以点为位似中心放大为原来的倍,得到,则等于(
)
A.
B.
C.
D.
7.下列相似图形不是位似图形的是(
)
A.
B.
C.
D.
8.如图所示的四边形,与选项中的四边形一定相似的是( )
A.
B.
C.
D.
二、填空题
9.如图所示的两个五边形相似,则_____,______,_______,______.
10.如图,用放大镜将图形放大,应属于哪一种变换:_________(请选填:对称变换、平移变换、旋转变换、相似变换).
11.把△ABC三点坐标A(0,1)、B(2,0)、C(3,2)分别乘以3得△A'B'C',的坐标A',(0,3)、B'(6,0)、C(9,6),那么△ABC与△A'B'C'是______图形,位似中心是_______,相似比为________
12.如图,已知与是相似比为的位似图形,点O为位似中心,若内一点与内一点是一对对应点,则点的坐标是______.
13.如图,△OAB与△OCD是以点O为位似中心的位似图形,相似比为3∶4,∠OCD=90°,∠AOB=60°,若点B的坐标是(6,0),则点C的坐标是______.
14.一个四边形的边长分别是3,4,5,6,另一个与它形状相同的四边形最小边长为6,则另一个四边形的周长是________.
15.如图,矩形的两边在坐标轴上,点为平面直角坐标系的原点,以轴上的某一点为位似中心,作位似图形,且点的坐标,则位似中心的坐标为__________.
16.如图,△ABC与△DEF位似,位似中心为点O,且BC:EF=3:2,则S△ABC:S△DEF=_____.
三、解答题
17.观察图中①~⑩的图形,其中哪些图形分别与(1),(2),(3),(4)相似?
(1)
(2)
(3)
(4)
①
②
③
④
⑤
⑥
⑦
⑧
⑨
⑩
18.如图,所示的两个矩形是否相似?并简单说明理由.
19.画图:点,把以点为位似中心放大到原来的倍,且写出对应顶点的坐标.
20.如图,已知五边形A'B'C'D'E'是五边形的位似图形,但被小玮擦去了一部分,你能将它补完整吗?
21.在一张比例尺为的地图上,有一块多边形区域的周长是,面积是,求这个区域的实际周长和面积.
22.如图,△DEF是△ABC经过位似变换得到的,位似中心是点O,请确定点O的位置,如果OC=3.6
cm,OF=2.4
cm,求它们的相似比.
23.如图,在6×8的网格中,每个小正方形的边长均为1,点O和△ABC的顶点均为小正方形的顶点.
(1)在图中△ABC的内部作△A′B′C′,使△A′B′C′和△ABC位似,且位似中心为点O,位似比为1:2;
(2)连接(1)中的AA′,则线段AA′的长度是________.
24.如图,是由经过位似变换得到的
(1)求出与的相似比,并指出它们的位似中心;
(2)是的位似图形吗?如果是,求相似比;如果不是说明理由;
(3)如果相似比为,那么的位似图形是什么?
试卷第2页,共2页
参考答案
1.C
【解析】解:大小不同,形状相同,所以是相似图形,故A选项错误;
大小不同,形状相同,所以是相似图形,故B选项错误;
大小不同,形状不相同,所以不是相似图形,故C选项正确;
大小不同,形状相同,所以是相似图形,故D选项错误.
故选:C.
2.B
【解析】解:由图可知,对应边AG与CE的延长线交于点B,
∴点B为位似中心
故选B.
3.D
【解析】解:如图,位似中心是点P.
故选D
4.D
【解析】解:A、邻边对应成比例的两个平行四边形,对应的角不一定相等,因而不一定相似,故错误,不符合题意;
B、有一条边相等的两个矩形,对应边的比不一定相等,因而不一定相似,故错误,不符合题意;;
C、有一个内角对应相等的两个平行四边形,对应边的比不一定相等,故错误,不符合题意;;
D、底角都是60°的等腰三角形一定是等边三角形,因而一定相似,故正确,符合题意;.
故选:D.
5.A
【解析】解:∵直角三角形的两直角边之比为2:3,
∴虽不能确定两直角边的值,但能确定其比值,
∴能确定该直角三角形的形状,
故选:A.
6.C
【解析】∵
将以点为位似中心放大为原来的倍,得到,
∴
与的位似比为,
则=.
故选:C
7.D
【解析】解:D中两个图形,对应边不互相平行,不是位似图形,
A、B、C中的图形符合位似变换的定义,是位似图形,
故选:D.
8.D
【解析】作AE⊥BC于E,
则四边形AECD为矩形,
∴EC=AD=1,AE=CD=3,
∴BE=4,
由勾股定理得,AB==5,
∴四边形ABCD的四条边之比为1:3:5:5,
D选项中,四条边之比为1:3:5:5,且对应角相等,
故选:D.
9.3
4.5
4
6
【解析】解:∵两个五边形相似,
∴,,,,
解得,a=3,b=4.5,c=4,d=6.
10.相似变换
【解析】由一个图形到另一个图形,在改变的过程中形状不变,大小产生变化,属于相似变化.
故答案为相似变换.
11.位似
原点O
3
【解析】
根据题意在平面直角坐标系中可以画出图形,可得:
△ABC与△A'B'C'是位似图形,位似中心是原点O,相似比为3.
故答案为:位似;
原点O;
3.
12.
【解析】∵P(x,y),相似比为1:2,点O为位似中心,
∴P′的坐标是( 2x, 2y).故答案为( 2x, 2y).
13.(2,2)
【解析】分别过A、C作AE⊥OB,CF⊥OB,
∵∠OCD=90°,∠AOB=60°,
∴∠ABO=∠CDO=30°,∠OCF=30°,
∵△OAB与△OCD是以点O为位似中心的位似图形,相似比为3:4,点B的坐标是(6,0),
∴D(8,0),则DO=8,
故OC=4,
则FO=2,CF=CO cos30°=4×=2,
故点C的坐标是:(2,2).
故答案为:(2,2).
14.36
【解析】根据对应边成比例,得出该四边形的另三条边的长分别是8,10,12.所以周长为6+8+10+12=36.
15.
【解析】解:如图所示,连接BF交y轴于P,
∵四边形ABCD和四边形EFGO是矩形,点B,F的坐标分别为( 4,4),(2,1),
∴点C的坐标为(0,4),点G的坐标为(0,1),
∴CG=3,
∵BC∥GF,
∴△PGF∽△PCB,
∴GP:PC=GF:BC=1:2,
∴GP=1,PC=2,
∴OP=2,
∴点P的坐标为(0,2),
即:位似中心的坐标为(0,2).
故答案为(0,2).
16.9:4
【解析】解:∵△ABC与△DEF位似,
∴△ABC∽△DEF,
∵BC:EF=3:2,
∴
,
故答案为:9:4.
17.与(1)相似的图形是⑦;与(2)相似的图形是①⑧;与(3)相似的图形是②④;与(4)相似的图形是⑩.
【解析】解:与(1)相似的图形是⑦;
与(2)相似的图形是①⑧;
与(3)相似的图形是②④;
与(4)相似的图形是⑩.
18.相似,见解析
【解析】解:相似.
理由:这两个的角是直角,因而对应角相等一定是正确的,
小矩形的长是20-5-5=10,宽是12-3-3=6,
因为,即两个矩形的对应边的比相等,
因而这两个矩形相似.
19.作图见解析,,,或,,.
【解析】解:延长到,使,得到点的对应点,
同法得到点的对应点,点的对应点不变,连接,
就是所求的三角形;
或反向延长或,由同样的方法得到的对应点
连接就是所求的三角形;
由,
,,.
或,,.
20.补充图形见解析
【解析】解:如图,分别延长AA′、BB′,它们相交于点O,再过点A作AE∥A′E′交OE′的延长线于E,过点B′作B′C′∥BC′交OC于C′,过点C′作C′D′∥CD交OD于D′,然后连接DE、D′E′即可.
21.周长480cm,面积8000
cm2
【解析】设实际周长是,则:
,
解得:();
面积之比等于相似比的平方,设实际面积是平方厘米,则:
,
解得:()
.
22.3∶2.
【解析】解:连接AD,CF交于点O,
则点O即为所求;
∵OC=3.6
cm,OF=2.4
cm,
∴OC:OF=3∶2,
∴△ABC与△DEF的相似比为3∶2.
23.(1)作图见解析;(2).
【解析】(1)如下图,△A′B′C′为所作;
(2)由图结合勾股定理可得:AO=,
∵点OA′:OA=1:2,
∴OA′=OA=,
∴AA′=OA-OA′=.
24.;它们的位似中心是;(2)是的位似图形,相似比为;(3)如果相似比为,那么的位似图形是.
【解析】与的相似比为:;它们的位似中心是;
(2)是的位似图形,
相似比为:;
(3)如果相似比为,那么的位似图形是.
答案第1页,共2页
答案第1页,共2页
同课章节目录
- 第23章 数据分析
- 23.1 平均数与加权平均数
- 23.2 中位数与众数
- 23.3 方差
- 23.4 用样本估计总体
- 第24章 一元二次方程
- 24.1 一元二次方程
- 24.2 解一元二次方程
- 24.3 一元二次方程根与系数的关系
- 24.4 一元二次方程的应用
- 第25章 图形的相似
- 25.1 比例线段
- 25.2 平行线分线段成比例
- 25.3 相似三角形
- 25.4 相似三角形的判定
- 25.5 相似三角形的性质
- 25.6 相似三角形的应用
- 25.7 相似多边形和图形的位似
- 第26章 解直角三角形
- 26.1 锐角三角函数
- 26.2 锐角三角函数的计算
- 26.3 解直角三角形
- 26.4 解直角三角形的应用
- 第27章 反比例函数
- 27.1 反比例函数
- 27.2 反比例函数的图像和性质
- 27.3 反比例函数的应用
- 第28章 圆
- 28.1 圆的概念和性质
- 28.2 过三点的圆
- 28.3 圆心角和圆周角
- 28.4 垂径定理
- 28.5 弧长和扇形面积
