冀教版八年级上期末数学模拟试卷2(word版、含解析)
文档属性
| 名称 | 冀教版八年级上期末数学模拟试卷2(word版、含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 384.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-06 09:36:41 | ||
图片预览




文档简介
冀教版八年级(上)期末数学模拟试卷
一、选择题:(本大题共
16
个小题,每小题
2
分,共
32
分.在每小题给出的四个选项中只有一项是符合题目要求的,请将它的代号填在题后的括号内.)
1.(2
分)8
的平方根是(
)
A.4
B.±4
C.2
D.
2.(2
分)下列运算中错误的是(
)
A.
+
=
B.
×
=
C.
÷
=2
D.
=3
3.(2
分)下列基本图形既是轴对称图形又是中心对称图形的是(
)
A.
B.
C.
D.
4.(2
分)如图,△ABC
中,AB=5,AC=6,BC=4,边
AB
的垂直平分线交
AC
于点
D,则△BDC
的周长是(
)
A.8
B.9
C.10
D.11
5.(2
分)下列各式中属于最简二次根式的是(
)
A.
B.
C.
D.
6.(2
分)如图所示,将正方形纸片三次对折后,沿图中
AB
线剪掉一个等腰直角三角形,展开铺平得到的图形是(
)
A.
B.
C.
D.
7.(2
分)计算的结果是(
)
A.
+
B.
C.
D.
﹣
8.(2
分)某工程队准备修建一条长
1200m
的道路,由于采用新的施工方式,实际每天修建道路的速度比原计划快
20%,结果提前
2
天完成任务.若设原计划每天修建道路
xm,则根据题意可列方程为
(
)
A.
﹣
=2
B.
﹣
=2
C.
﹣
=2
D.
﹣
=2
9.(2
分)如图,在△ABC
中,AB=AC,且
D
为
BC
上一点,CD=AD,AB=BD,则∠B
的度数为
(
)
A.30°
B.36°
C.40°
D.45°
10.(2
分)下列各组二次根式中,能合并的两个二次根式是(
)
A.
和
B.
和
C.
和
D.
和
11.(2
分)如图,在△ABC
中,AB=AC,∠A=30°,以
B
为圆心,BC
的长为半径圆弧,交
AC
于点
D,连接
BD,则∠ABD=(
)
A.30°
B.60°
C.45°
D.90°
12.(2
分)若,则
b
的取值范围是(
)
A.b≥0
B.b≥3
C.b≤3
D.b>3
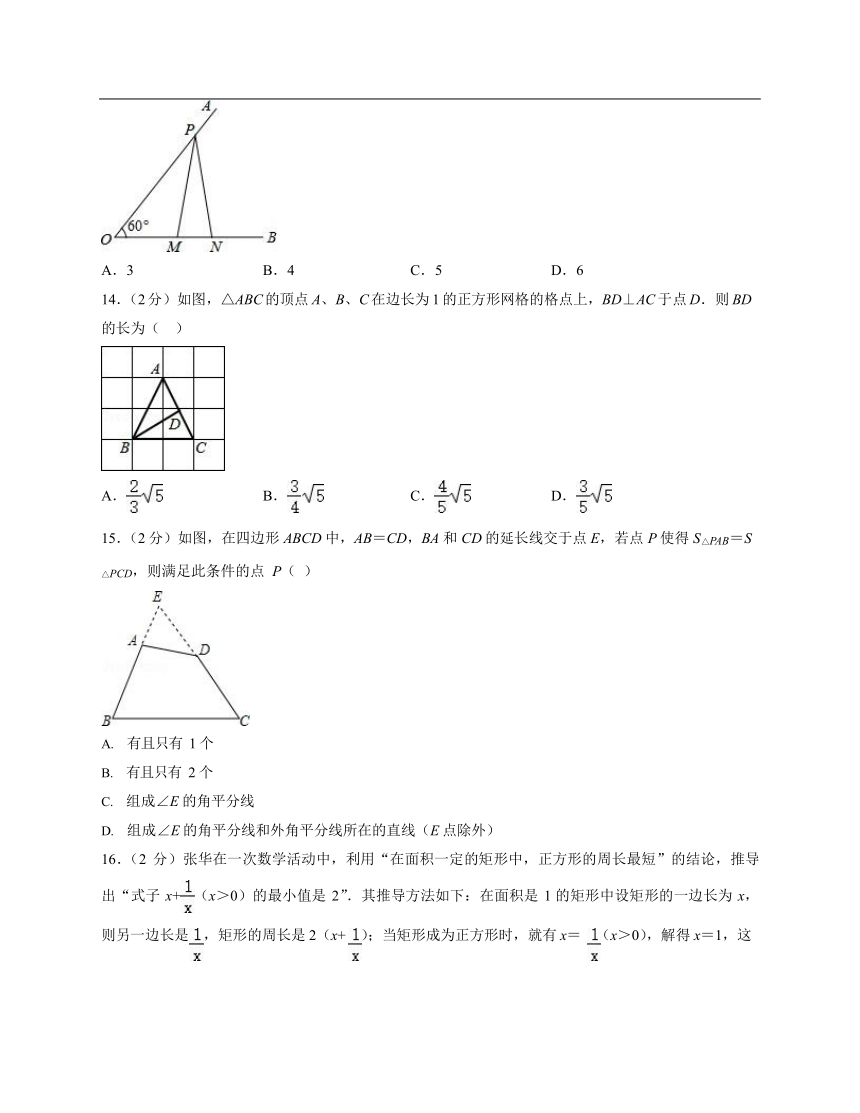
13.(2
分)如图,已知∠AOB=60°,点
P
在边
OA
上,OP=12,点
M,N
在边
OB
上,PM=PN,若
MN=2,
则
OM=(
)
A.3
B.4
C.5
D.6
14.(2
分)如图,△ABC
的顶点
A、B、C
在边长为
1
的正方形网格的格点上,BD⊥AC
于点
D.则
BD
的长为(
)
A.
B.
C.
D.
15.(2
分)如图,在四边形
ABCD
中,AB=CD,BA
和
CD
的延长线交于点
E,若点
P
使得
S△PAB=S
△PCD,则满足此条件的点
P(
)
有且只有
1
个
有且只有
2
个
组成∠E
的角平分线
组成∠E
的角平分线和外角平分线所在的直线(E
点除外)
16.(2
分)张华在一次数学活动中,利用“在面积一定的矩形中,正方形的周长最短”的结论,推导出“式子
x+(x>0)的最小值是
2”.其推导方法如下:在面积是
1
的矩形中设矩形的一边长为
x,则另一边长是
,矩形的周长是
2(x+
);当矩形成为正方形时,就有
x=
(x>0),解得
x=1,这
时矩形的周长
2(x+)=4
最小,因此
x+(x>0)的最小值是
2.模仿张华的推导,你求得式子
(x>0)的最小值是(
)
A.2
B.1
C.6
D.10
二、填空题:(本大题共
4
个小题,每小题
3
分,共
12
分.把答案写在题中横线上)
17.(3
分)已知:(a+6)2+=0,则
2b2﹣4b﹣a
的值为
.
18.(3
分)如图,Rt△ABC
中,AB=9,BC=6,∠B=90°,将△ABC
折叠,使
A
点与
BC
的中点
D
重合,折痕为
MN,则线段
BN
的长为
.
19.(3
分)如图,一只蚂蚁从点
A
沿数轴向右直爬
2
个单位到达点
B,点
A
表示﹣,设点
B
所表示的数为
m,则(m﹣1)(m﹣3)的值为
.
20.(3
分)下面是一个按某种规律排列的数表:
第
1
行
1
第
2
行
2
第
3
行
2
3
第
4
行
2
4
…
…
那么第
5
行中的第
2
个数是
,第
n(n>1,且
n
是整数)行的第
2
个数是
.(用含
n
的代数式表示)
三、解答题:(本大题共
6
个小题,共
56
分.解答应写出文字说明、证明过程或演算步骤)
21.(8
分)当
a=
,求代数式的值.
22.(9
分)在如图所示的方格纸中,每个小方格都是边长为
1
个单位的正方形,△ABC
的三个顶点都在格点上(每个小方格的顶点叫格点)
画出△ABC
关于直线
l
对称的图形△A1B1C1;
画出△ABC
关于点
O
中心对称的图形△A2B2C2,并标出点
M
的对称点
M′;
直接写出线段
MM′的长度.
23.(9
分)在本学期我们学习了角平分线的性质定理和判定定理,那么,你还是否记得它们的具体内容.
请把下面两个定理所缺的内容补充完整:
角平分线性质定理:角平分线上的点到
的距离相等.
角平分线判定定理:到角的两边距离相等的点在
.
老师在黑板上画出了图形,把判定定理的已知、求证写在了黑板上,可是有些内容不完整,请你把内容补充完整
已知:如图
1,点
P
是∠AOB
内一点,PD⊥AO,PE⊥OB,垂足分别为
D、E,且
PD=
,求证:
点
P
在∠AOB
的
上
请你完成证明过程:
知识运用:如图
2,三条公路两两相交,现在要修建一加油站,使加油站到三条公路的距离相等,
加油站可选择的位置共有
处.
24.(9
分)兴发服装店老板用
4500
元购进一批某款
T
恤衫,由于深受顾客喜爱,很快售完,老板又用
4950
元购进第二批该款式
T
恤衫,所购数量与第一批相同,但每件进价比第一批多了
9
元.
第一批该款式
T
恤衫每件进价是多少元?
老板以每件
120
元的价格销售该款式
T
恤衫,当第二批
T
恤衫售出
时,出现了滞销,于是决定
降价促销,若要使第二批的销售利润不低于
650
元,剩余的
T
恤衫每件售价至少要多少元?(利润=
售价﹣进价)
25.(10
分)在一平直河岸
l
同侧有
A,B
两个村庄,A,B
到
l
的距离分别是
3km
和
2km,AB=akm(a
>1).现计划在河岸
l
上建一抽水站
P,用输水管向两个村庄供水.
方案设计
某班数学兴趣小组设计了两种铺设管道方案:图
1
是方案一的示意图,设该方案中管道长度为
d1,且d1=PB+BA(km)(其中
BP⊥l
于点
P);图
2
是方案二的示意图,设该方案中管道长度为
d2,且
d2=
PA+PB(km)(其中点
A′与点
A
关于
l
对称,A′B
与
l
交于点
P).
观察计算
在方案一中,d1=
km(用含
a
的式子表示)
在方案二中,组长小宇为了计算
d2
的长,作了如图
3
所示的辅助线,请你按小宇同学的思路计算,d2=
km(用含
a
的式子表示).
探索归纳
(1)①当
a=4
时,比较大小:d1
d2(填“>”、“=”或“<”);
②当
a=6
时,比较大小:d1
d2(填“>”、“=”或“<”);
(2)请你参考方框中的方法指导,就
a(当
a>1
时)的所有取值情况进行分析,要使铺设的管道长度较短,
应选择方案一还是方案二?
26.(11
分)(1)如图(1),已知:在△ABC
中,∠BAC=90°,AB=AC,直线
m
经过点
A,BD⊥直线
m,CE⊥直线
m,垂足分别为点
D、E.
证明:DE=BD+CE.
如图(2),将(1)中的条件改为:在△ABC
中,AB=AC,D、A、E
三点都在直线
m
上,并且
有∠BDA=∠AEC=∠BAC=α,其中
α
为任意锐角或钝角.请问结论
DE=BD+CE
是否成立?如成立,
请你给出证明;若不成立,请说明理由.
拓展与应用:如图(3),D、E
是
D、A、E
三点所在直线
m
上的两动点(D、A、E
三点互不重合),点
F
为∠BAC
平分线上的一点,且△ABF
和△ACF
均为等边三角形,连接
BD、CE,若∠BDA=
∠AEC=∠BAC,试判断△DEF
的形状并说明理由.
冀教版八年级(上)期末数学试卷
参考答案与试题解析
一、选择题:(本大题共
16
个小题,每小题
2
分,共
32
分.在每小题给出的四个选项中只有一项是符合题目要求的,请将它的代号填在题后的括号内.)
1.(2
分)8
的平方根是(
)
A.4
B.±4
C.2
D.
【解答】解:∵
,
∴8
的平方根是.
故选:D.
2.(2
分)下列运算中错误的是(
)
A.
+
=
B.
×
=
C.
÷
=2
D.
=3
【解答】解:A、
+
无法计算,故此选项正确;
B、
×
=
,正确,不合题意;
C、
÷
=2,正确,不合题意;
D、
=3,正确,不合题意.
故选:A.
3.(2
分)下列基本图形既是轴对称图形又是中心对称图形的是(
)
A.
B.
C.
D.
【解答】解:A、是轴对称图形,不是中心对称图形.故错误;
B、是轴对称图形,不是中心对称图形.故错误;
C、不是轴对称图形,是中心对称图形.故错误;
D、是轴对称图形,是中心对称图形.故正确.
故选:D.
4.(2
分)如图,△ABC
中,AB=5,AC=6,BC=4,边
AB
的垂直平分线交
AC
于点
D,则△BDC
的周长是(
)
A.8
B.9
C.10
D.11
【解答】解:设
AB
的中垂线与
AB
交于点
E,
∵ED
是
AB
的垂直平分线,
∴AD=BD,
∵△BDC
的周长=DB+BC+CD,
∴△BDC
的周长=AD+BC+CD=AC+BC=6+4=10.
故选:C.
5.(2
分)下列各式中属于最简二次根式的是(
)
A.
B.
C.
D.
【解答】解:B、
=
=|x|y2
,可化简;
C、
=
=2
,可化简;
D、
=
=
,可化简;
因此只有
A、是最简二次根式.
故选:A.
6.(2
分)如图所示,将正方形纸片三次对折后,沿图中
AB
线剪掉一个等腰直角三角形,展开铺平得到的图形是(
)
A.
B.
C.
D.
【解答】解:找一张正方形的纸片,按上述顺序折叠、裁剪,然后展开后得到的图形如图所示:
故选:A.
7.(2
分)计算的结果是(
)
A.
+
B.
C.
D.
﹣
【解答】解:原式=4×
+3×
﹣2
=
.
故选:B.
8.(2
分)某工程队准备修建一条长
1200m
的道路,由于采用新的施工方式,实际每天修建道路的速度比原计划快
20%,结果提前
2
天完成任务.若设原计划每天修建道路
xm,则根据题意可列方程为
(
)
A.
﹣
=2
B.
﹣
=2
C.
﹣
=2
D.
﹣
=2
【解答】解:设原计划每天修建道路
xm,则实际每天修建道路为(1+20%)xm,
由题意得,
﹣
=2.
故选:D.
9.(2
分)如图,在△ABC
中,AB=AC,且
D
为
BC
上一点,CD=AD,AB=BD,则∠B
的度数为
(
)
A.30°
B.36°
C.40°
D.45°
【解答】解:∵AB=AC,
∴∠B=∠C,
∵AB=BD,
∴∠BAD=∠BDA,
∵CD=AD,
∴∠C=∠CAD,
∵∠BAD+∠CAD+∠B+∠C=180°,
∴5∠B=180°,
∴∠B=36°
故选:B.
10.(2
分)下列各组二次根式中,能合并的两个二次根式是(
)
A.
和
B.
和
C.
和
D.
和
【解答】解:A、
,3
与
不能合并,故错误;
B、
,
与
能合并,正确;
C、
,
=|b|
,不能合并,故错误;
D、
与
不能合并,故错误;
故选:B.
11.(2
分)如图,在△ABC
中,AB=AC,∠A=30°,以
B
为圆心,BC
的长为半径圆弧,交
AC
于点
D,连接
BD,则∠ABD=(
)
A.30°
B.60°
C.45°
D.90°
【解答】解:∵在△ABC
中,AB=AC,∠A=30°,
∴∠ABC=∠ACB=75°,
又∵以
B
为圆心,BC
的长为半径圆弧,交
AC
于点
D,
∴∠DBC=2(90°﹣∠BDC)=2×(90°﹣75°)=30°,
又∵∠ABC=∠ABD+∠DBC,
∴∠ABD=75°﹣30°=45°,
故选:C.
12.(2
分)若
,则
b
的取值范围是(
)
A.b≥0
B.b≥3
C.b≤3
D.b>3
【解答】解:∵
,
∴3﹣b≥0,
∴b≤3.
故选:C.
13.(2
分)如图,已知∠AOB=60°,点
P
在边
OA
上,OP=12,点
M,N
在边
OB
上,PM=PN,若
MN=2,
则
OM=(
)
A.3
B.4
C.5
D.6
【解答】解:过
P
作
PD⊥OB,交
OB
于点
D,
在
Rt△OPD
中,cos60°==
,OP=12,
∴OD=6,
∵PM=PN,PD⊥MN,MN=2,
∴MD=ND=
MN=1,
∴OM=OD﹣MD=6﹣1=5.
故选:C.
14.(2
分)如图,△ABC
的顶点
A、B、C
在边长为
1
的正方形网格的格点上,BD⊥AC
于点
D.则
BD
的长为(
)
A.
B.
C.
D.
【解答】解:如图,由勾股定理得
AC==
.
∵
BC×2=
AC BD,即
×2×2=
×
BD
∴BD=
.
故选:C.
15.(2
分)如图,在四边形
ABCD
中,AB=CD,BA
和
CD
的延长线交于点
E,若点
P
使得
S△PAB=S
△PCD,则满足此条件的点
P(
)
有且只有
1
个
有且只有
2
个
组成∠E
的角平分线
组成∠E
的角平分线和外角平分线所在的直线(E
点除外)
【解答】解:作∠E
的平分线,
可得点
P
到
AB
和
CD
的距离相等,
因为
AB=CD,
所以此时点
P
满足
S△PAB=S△PCD.
组成∠E
的角平分线和外角平分线所在的直线(E
点除外)
故选:D.
16.(2
分)张华在一次数学活动中,利用“在面积一定的矩形中,正方形的周长最短”的结论,推导出“式子
x+(x>0)的最小值是
2”.其推导方法如下:在面积是
1
的矩形中设矩形的一边长为
x,则另一边长是,矩形的周长是
2(x+);当矩形成为正方形时,就有
x=(x>0),解得
x=1,这
时矩形的周长
2(x+)=4
最小,因此
x+
(x>0)的最小值是
2.模仿张华的推导,你求得式子
(x>0)的最小值是(
)
A.2
B.1
C.6
D.10
【解答】解:∵x>0,
∴在原式中分母分子同除以
x,
即
=x+
,
在面积是
9
的矩形中设矩形的一边长为
x,则另一边长是,
矩形的周长是
2(x+);
当矩形成为正方形时,就有
x=,(x>0),解得
x=3,
这时矩形的周长
2(x+)=12
最小,
因此
x+(x>0)的最小值是
6.
故选:C.
二、填空题:(本大题共
4
个小题,每小题
3
分,共
12
分.把答案写在题中横线上)
17.(3
分)已知:(a+6)2+=0,则
2b2﹣4b﹣a
的值为
12
.
【解答】解:∵(a+6)2+
=0,
∴a+6=0,b2﹣2b﹣3=0,
解得,a=﹣6,b2﹣2b=3,
可得
2b2﹣4b=6,
则
2b2﹣4b﹣a=6﹣(﹣6)=12,
故答案为:12.
18.(3
分)如图,Rt△ABC
中,AB=9,BC=6,∠B=90°,将△ABC
折叠,使
A
点与
BC
的中点
D
重合,折痕为
MN,则线段
BN
的长为
4
.
【解答】解:设
BN=x,由折叠的性质可得
DN=AN=9﹣x,
∵D
是
BC
的中点,
∴BD=3,
在
Rt△BND
中,x2+32=(9﹣x)2,
解得
x=4.
故线段
BN
的长为
4.
故答案为:4.
19.(3
分)如图,一只蚂蚁从点
A
沿数轴向右直爬
2
个单位到达点
B,点
A
表示﹣,设点
B
所表示的数为
m,则(m﹣1)(m﹣3)的值为
1
.
【解答】解:由题意得:m=﹣
+2,
(m﹣1)(m﹣3)
=(﹣+2﹣1)(﹣+2﹣3)
=(1﹣)(﹣1﹣)
=2﹣1
=1,
故答案为:1.
20.(3
分)下面是一个按某种规律排列的数表:
第
1
行
1
第
2
行
2
第
3
行
2
3
第
4
行
2
4
…
…
那么第
5
行中的第
2
个数是
3
,第
n(n>1,且
n
是整数)
行的第
2
个数
是
.(用含
n
的代数式表示)
【解答】解:第五行的第二个数是
,
第
n
行的第二个数的算术平方根是
,
故答案为:3
,
.
三、解答题:(本大题共
6
个小题,共
56
分.解答应写出文字说明、证明过程或演算步骤)
21.(8
分)当
a=
,求代数式
的值.
【解答】解:a=(+2)(2﹣)2+
=(2+)(2﹣)(2﹣)+
=1×(2﹣
)+
=2,
原式=
=
当
a=2
时,原式=2.
22.(9
分)在如图所示的方格纸中,每个小方格都是边长为
1
个单位的正方形,△ABC
的三个顶点都在格点上(每个小方格的顶点叫格点)
画出△ABC
关于直线
l
对称的图形△A1B1C1;
画出△ABC
关于点
O
中心对称的图形△A2B2C2,并标出点
M
的对称点
M′;
直接写出线段
MM′的长度.
【解答】解:(1)△A1B1C1如图所示;
(2)△A2B2C2
如图所示;
(3)MM′=
=2
.
23.(9
分)在本学期我们学习了角平分线的性质定理和判定定理,那么,你还是否记得它们的具体内容.
请把下面两个定理所缺的内容补充完整:
角平分线性质定理:角平分线上的点到
这个角的两边
的距离相等.
角平分线判定定理:到角的两边距离相等的点在
角平分线上
.
老师在黑板上画出了图形,把判定定理的已知、求证写在了黑板上,可是有些内容不完整,请你把内容补充完整
已知:如图
1,点
P
是∠AOB
内一点,PD⊥AO,PE⊥OB,垂足分别为
D、E,且
PD=
PE
,求证:
点
P
在∠AOB
的
平分线上
上
请你完成证明过程:
知识运用:如图
2,三条公路两两相交,现在要修建一加油站,使加油站到三条公路的距离相等,
加油站可选择的位置共有
4
处.
【解答】解:(1)角平分线性质定理:角平分线上的点到这个角的两边的距离相等.角平分线判定定理:到角的两边距离相等的点在角平分线上,
故答案为:这个角的两边;角平分线上;
已知:如图
1,点
P
是∠AOB
内一点,PD⊥AO,PE⊥OB,垂足分别为
D、E,且
PD=PE,求
证:点
P
在∠AOB
的平分线上.
故答案为:PE;平分线上;
如图:作射线
OP,
∵PD⊥AO,PE⊥OB,
∴∠PDO=∠PEO=90°,
在
Rt△OPD
和
Rt△OPE
中,
,
∴Rt△OPD≌Rt△OPE,
∴∠DOP=∠EOP,
∴OP
是∠AOB
的平分线,即点
P
在∠AOB
平分线上;
如图
2,M、N、G、H
即为所求,
故答案为:4.
24.(9
分)兴发服装店老板用
4500
元购进一批某款
T
恤衫,由于深受顾客喜爱,很快售完,老板又用
4950
元购进第二批该款式
T
恤衫,所购数量与第一批相同,但每件进价比第一批多了
9
元.
第一批该款式
T
恤衫每件进价是多少元?
老板以每件
120
元的价格销售该款式
T
恤衫,当第二批
T
恤衫售出时,出现了滞销,于是决定降价促销,若要使第二批的销售利润不低于
650
元,剩余的
T
恤衫每件售价至少要多少元?(利润=
售价﹣进价)
【解答】解:(1)设第一批
T
恤衫每件进价是
x
元,由题意,得
=
,
解得
x=90,
经检验
x=90
是分式方程的解,符合题意.
答:第一批
T
恤衫每件的进价是
90
元;
(2)设剩余的
T
恤衫每件售价
y
元.
由(1)知,第二批购进
=50(件).
由题意,得
120×50×+y×50×
﹣4950≥650,
解得
y≥80.
答:剩余的
T
恤衫每件售价至少要
80
元.
25.(10
分)在一平直河岸
l
同侧有
A,B
两个村庄,A,B
到
l
的距离分别是
3km
和
2km,AB=akm(a
>1).现计划在河岸
l
上建一抽水站
P,用输水管向两个村庄供水.
方案设计
某班数学兴趣小组设计了两种铺设管道方案:图
1
是方案一的示意图,设该方案中管道长度为
d1,且d1=PB+BA(km)(其中
BP⊥l
于点
P);图
2
是方案二的示意图,设该方案中管道长度为
d2,且
d2=
PA+PB(km)(其中点
A′与点
A
关于
l
对称,A′B
与
l
交于点
P).
观察计算
在方案一中,d1=
a+2
km(用含
a
的式子表示)
在方案二中,组长小宇为了计算
d2
的长,作了如图
3
所示的辅助线,请你按小宇同学的思路计算,d2=
km(用含
a
的式子表示).
探索归纳
(1)①当
a=4
时,比较大小:d1
<
d2(填“>”、“=”或“<”);
②当
a=6
时,比较大小:d1
>
d2(填“>”、“=”或“<”);
(2)请你参考方框中的方法指导,就
a(当
a>1
时)的所有取值情况进行分析,要使铺设的管道长度
较短,
应选择方案一还是方案二?
【解答】解:(1)∵如图
1,作
A
关于执行
l
的对称点
A′,连接
PA′,
∵A
和
A'关于直线
l
对称,
∴PA=PA',
d1=PB+BA=PB+PA'=a+2;
故答案为:a+2;
(2)
因
为
BK2=a2﹣1,
A'B2=BK2+A'K2=a2﹣1+52=a2+24
所以
d2=;
故答案为:
;
探索归纳:
(1)①当
a=4
时,d1=6,d2=,d1<d2;
②当
a=6
时,d1=8,d2=,d1>d2;
故答案为:<,>;
(2)d12﹣d22=(a+2)2﹣(
)2=4a﹣20.
①当
4a﹣20>0,即
a>5
时,d12﹣d22>0,
∴d1﹣d2>0,
∴d1>d2;
②当
4a﹣20=0,即
a=5
时,d12﹣d22=0,
∴d1﹣d2=0,
∴d1=d2
③当
4a﹣20<0,即
a<5
时,d12﹣d22<0,
∴d1﹣d2<0,
∴d1<d2
综上可知:当
a>5
时,选方案二;
当
a=5
时,选方案一或方案二;
当
1<a<5
时,选方案一.
26.(11
分)(1)如图(1),已知:在△ABC
中,∠BAC=90°,AB=AC,直线
m
经过点
A,BD⊥直线
m,CE⊥直线
m,垂足分别为点
D、E.
证明:DE=BD+CE.
如图(2),将(1)中的条件改为:在△ABC
中,AB=AC,D、A、E
三点都在直线
m
上,并且
有∠BDA=∠AEC=∠BAC=α,其中
α
为任意锐角或钝角.请问结论
DE=BD+CE
是否成立?如成立,
请你给出证明;若不成立,请说明理由.
拓展与应用:如图(3),D、E
是
D、A、E
三点所在直线
m
上的两动点(D、A、E
三点互不重合),点
F
为∠BAC
平分线上的一点,且△ABF
和△ACF
均为等边三角形,连接
BD、CE,若∠BDA=
∠AEC=∠BAC,试判断△DEF
的形状并说明理由.
【解答】解:(1)如图
1,∵BD⊥直线
m,CE⊥直线
m,
∴∠BDA=∠CEA=90°,
∵∠BAC=90°,
∴∠BAD+∠CAE=90°
∵∠BAD+∠ABD=90°,
∴∠CAE=∠ABD,
在△ADB
和△CEA
中,
,
∴△ADB≌△CEA(AAS),
∴AE=BD,AD=CE,
∴DE=AE+AD=BD+CE;
如图
2,∵∠BDA=∠BAC=α,
∴∠DBA+∠BAD=∠BAD+∠CAE=180°﹣α,
∴∠DBA=∠CAE,
在△ADB
和△CEA
中,
,
∴△ADB≌△CEA(AAS),
∴AE=BD,AD=CE,
∴DE=AE+AD=BD+CE;
如图
3,由(2)可知,△ADB≌△CEA,
∴BD=AE,∠DBA=∠CAE,
∵△ABF
和△ACF
均为等边三角形,
∴∠ABF=∠CAF=60°,BF=AF,
∴∠DBA+∠ABF=∠CAE+∠CAF,
∴∠DBF=∠FAE,
∵在△DBF
和△EAF
中,
,
∴△DBF≌△EAF(SAS),
∴DF=EF,∠BFD=∠AFE,
∴∠DFE=∠DFA+∠AFE=∠DFA+∠BFD=60°,
∴△DEF
为等边三角形.
一、选择题:(本大题共
16
个小题,每小题
2
分,共
32
分.在每小题给出的四个选项中只有一项是符合题目要求的,请将它的代号填在题后的括号内.)
1.(2
分)8
的平方根是(
)
A.4
B.±4
C.2
D.
2.(2
分)下列运算中错误的是(
)
A.
+
=
B.
×
=
C.
÷
=2
D.
=3
3.(2
分)下列基本图形既是轴对称图形又是中心对称图形的是(
)
A.
B.
C.
D.
4.(2
分)如图,△ABC
中,AB=5,AC=6,BC=4,边
AB
的垂直平分线交
AC
于点
D,则△BDC
的周长是(
)
A.8
B.9
C.10
D.11
5.(2
分)下列各式中属于最简二次根式的是(
)
A.
B.
C.
D.
6.(2
分)如图所示,将正方形纸片三次对折后,沿图中
AB
线剪掉一个等腰直角三角形,展开铺平得到的图形是(
)
A.
B.
C.
D.
7.(2
分)计算的结果是(
)
A.
+
B.
C.
D.
﹣
8.(2
分)某工程队准备修建一条长
1200m
的道路,由于采用新的施工方式,实际每天修建道路的速度比原计划快
20%,结果提前
2
天完成任务.若设原计划每天修建道路
xm,则根据题意可列方程为
(
)
A.
﹣
=2
B.
﹣
=2
C.
﹣
=2
D.
﹣
=2
9.(2
分)如图,在△ABC
中,AB=AC,且
D
为
BC
上一点,CD=AD,AB=BD,则∠B
的度数为
(
)
A.30°
B.36°
C.40°
D.45°
10.(2
分)下列各组二次根式中,能合并的两个二次根式是(
)
A.
和
B.
和
C.
和
D.
和
11.(2
分)如图,在△ABC
中,AB=AC,∠A=30°,以
B
为圆心,BC
的长为半径圆弧,交
AC
于点
D,连接
BD,则∠ABD=(
)
A.30°
B.60°
C.45°
D.90°
12.(2
分)若,则
b
的取值范围是(
)
A.b≥0
B.b≥3
C.b≤3
D.b>3
13.(2
分)如图,已知∠AOB=60°,点
P
在边
OA
上,OP=12,点
M,N
在边
OB
上,PM=PN,若
MN=2,
则
OM=(
)
A.3
B.4
C.5
D.6
14.(2
分)如图,△ABC
的顶点
A、B、C
在边长为
1
的正方形网格的格点上,BD⊥AC
于点
D.则
BD
的长为(
)
A.
B.
C.
D.
15.(2
分)如图,在四边形
ABCD
中,AB=CD,BA
和
CD
的延长线交于点
E,若点
P
使得
S△PAB=S
△PCD,则满足此条件的点
P(
)
有且只有
1
个
有且只有
2
个
组成∠E
的角平分线
组成∠E
的角平分线和外角平分线所在的直线(E
点除外)
16.(2
分)张华在一次数学活动中,利用“在面积一定的矩形中,正方形的周长最短”的结论,推导出“式子
x+(x>0)的最小值是
2”.其推导方法如下:在面积是
1
的矩形中设矩形的一边长为
x,则另一边长是
,矩形的周长是
2(x+
);当矩形成为正方形时,就有
x=
(x>0),解得
x=1,这
时矩形的周长
2(x+)=4
最小,因此
x+(x>0)的最小值是
2.模仿张华的推导,你求得式子
(x>0)的最小值是(
)
A.2
B.1
C.6
D.10
二、填空题:(本大题共
4
个小题,每小题
3
分,共
12
分.把答案写在题中横线上)
17.(3
分)已知:(a+6)2+=0,则
2b2﹣4b﹣a
的值为
.
18.(3
分)如图,Rt△ABC
中,AB=9,BC=6,∠B=90°,将△ABC
折叠,使
A
点与
BC
的中点
D
重合,折痕为
MN,则线段
BN
的长为
.
19.(3
分)如图,一只蚂蚁从点
A
沿数轴向右直爬
2
个单位到达点
B,点
A
表示﹣,设点
B
所表示的数为
m,则(m﹣1)(m﹣3)的值为
.
20.(3
分)下面是一个按某种规律排列的数表:
第
1
行
1
第
2
行
2
第
3
行
2
3
第
4
行
2
4
…
…
那么第
5
行中的第
2
个数是
,第
n(n>1,且
n
是整数)行的第
2
个数是
.(用含
n
的代数式表示)
三、解答题:(本大题共
6
个小题,共
56
分.解答应写出文字说明、证明过程或演算步骤)
21.(8
分)当
a=
,求代数式的值.
22.(9
分)在如图所示的方格纸中,每个小方格都是边长为
1
个单位的正方形,△ABC
的三个顶点都在格点上(每个小方格的顶点叫格点)
画出△ABC
关于直线
l
对称的图形△A1B1C1;
画出△ABC
关于点
O
中心对称的图形△A2B2C2,并标出点
M
的对称点
M′;
直接写出线段
MM′的长度.
23.(9
分)在本学期我们学习了角平分线的性质定理和判定定理,那么,你还是否记得它们的具体内容.
请把下面两个定理所缺的内容补充完整:
角平分线性质定理:角平分线上的点到
的距离相等.
角平分线判定定理:到角的两边距离相等的点在
.
老师在黑板上画出了图形,把判定定理的已知、求证写在了黑板上,可是有些内容不完整,请你把内容补充完整
已知:如图
1,点
P
是∠AOB
内一点,PD⊥AO,PE⊥OB,垂足分别为
D、E,且
PD=
,求证:
点
P
在∠AOB
的
上
请你完成证明过程:
知识运用:如图
2,三条公路两两相交,现在要修建一加油站,使加油站到三条公路的距离相等,
加油站可选择的位置共有
处.
24.(9
分)兴发服装店老板用
4500
元购进一批某款
T
恤衫,由于深受顾客喜爱,很快售完,老板又用
4950
元购进第二批该款式
T
恤衫,所购数量与第一批相同,但每件进价比第一批多了
9
元.
第一批该款式
T
恤衫每件进价是多少元?
老板以每件
120
元的价格销售该款式
T
恤衫,当第二批
T
恤衫售出
时,出现了滞销,于是决定
降价促销,若要使第二批的销售利润不低于
650
元,剩余的
T
恤衫每件售价至少要多少元?(利润=
售价﹣进价)
25.(10
分)在一平直河岸
l
同侧有
A,B
两个村庄,A,B
到
l
的距离分别是
3km
和
2km,AB=akm(a
>1).现计划在河岸
l
上建一抽水站
P,用输水管向两个村庄供水.
方案设计
某班数学兴趣小组设计了两种铺设管道方案:图
1
是方案一的示意图,设该方案中管道长度为
d1,且d1=PB+BA(km)(其中
BP⊥l
于点
P);图
2
是方案二的示意图,设该方案中管道长度为
d2,且
d2=
PA+PB(km)(其中点
A′与点
A
关于
l
对称,A′B
与
l
交于点
P).
观察计算
在方案一中,d1=
km(用含
a
的式子表示)
在方案二中,组长小宇为了计算
d2
的长,作了如图
3
所示的辅助线,请你按小宇同学的思路计算,d2=
km(用含
a
的式子表示).
探索归纳
(1)①当
a=4
时,比较大小:d1
d2(填“>”、“=”或“<”);
②当
a=6
时,比较大小:d1
d2(填“>”、“=”或“<”);
(2)请你参考方框中的方法指导,就
a(当
a>1
时)的所有取值情况进行分析,要使铺设的管道长度较短,
应选择方案一还是方案二?
26.(11
分)(1)如图(1),已知:在△ABC
中,∠BAC=90°,AB=AC,直线
m
经过点
A,BD⊥直线
m,CE⊥直线
m,垂足分别为点
D、E.
证明:DE=BD+CE.
如图(2),将(1)中的条件改为:在△ABC
中,AB=AC,D、A、E
三点都在直线
m
上,并且
有∠BDA=∠AEC=∠BAC=α,其中
α
为任意锐角或钝角.请问结论
DE=BD+CE
是否成立?如成立,
请你给出证明;若不成立,请说明理由.
拓展与应用:如图(3),D、E
是
D、A、E
三点所在直线
m
上的两动点(D、A、E
三点互不重合),点
F
为∠BAC
平分线上的一点,且△ABF
和△ACF
均为等边三角形,连接
BD、CE,若∠BDA=
∠AEC=∠BAC,试判断△DEF
的形状并说明理由.
冀教版八年级(上)期末数学试卷
参考答案与试题解析
一、选择题:(本大题共
16
个小题,每小题
2
分,共
32
分.在每小题给出的四个选项中只有一项是符合题目要求的,请将它的代号填在题后的括号内.)
1.(2
分)8
的平方根是(
)
A.4
B.±4
C.2
D.
【解答】解:∵
,
∴8
的平方根是.
故选:D.
2.(2
分)下列运算中错误的是(
)
A.
+
=
B.
×
=
C.
÷
=2
D.
=3
【解答】解:A、
+
无法计算,故此选项正确;
B、
×
=
,正确,不合题意;
C、
÷
=2,正确,不合题意;
D、
=3,正确,不合题意.
故选:A.
3.(2
分)下列基本图形既是轴对称图形又是中心对称图形的是(
)
A.
B.
C.
D.
【解答】解:A、是轴对称图形,不是中心对称图形.故错误;
B、是轴对称图形,不是中心对称图形.故错误;
C、不是轴对称图形,是中心对称图形.故错误;
D、是轴对称图形,是中心对称图形.故正确.
故选:D.
4.(2
分)如图,△ABC
中,AB=5,AC=6,BC=4,边
AB
的垂直平分线交
AC
于点
D,则△BDC
的周长是(
)
A.8
B.9
C.10
D.11
【解答】解:设
AB
的中垂线与
AB
交于点
E,
∵ED
是
AB
的垂直平分线,
∴AD=BD,
∵△BDC
的周长=DB+BC+CD,
∴△BDC
的周长=AD+BC+CD=AC+BC=6+4=10.
故选:C.
5.(2
分)下列各式中属于最简二次根式的是(
)
A.
B.
C.
D.
【解答】解:B、
=
=|x|y2
,可化简;
C、
=
=2
,可化简;
D、
=
=
,可化简;
因此只有
A、是最简二次根式.
故选:A.
6.(2
分)如图所示,将正方形纸片三次对折后,沿图中
AB
线剪掉一个等腰直角三角形,展开铺平得到的图形是(
)
A.
B.
C.
D.
【解答】解:找一张正方形的纸片,按上述顺序折叠、裁剪,然后展开后得到的图形如图所示:
故选:A.
7.(2
分)计算的结果是(
)
A.
+
B.
C.
D.
﹣
【解答】解:原式=4×
+3×
﹣2
=
.
故选:B.
8.(2
分)某工程队准备修建一条长
1200m
的道路,由于采用新的施工方式,实际每天修建道路的速度比原计划快
20%,结果提前
2
天完成任务.若设原计划每天修建道路
xm,则根据题意可列方程为
(
)
A.
﹣
=2
B.
﹣
=2
C.
﹣
=2
D.
﹣
=2
【解答】解:设原计划每天修建道路
xm,则实际每天修建道路为(1+20%)xm,
由题意得,
﹣
=2.
故选:D.
9.(2
分)如图,在△ABC
中,AB=AC,且
D
为
BC
上一点,CD=AD,AB=BD,则∠B
的度数为
(
)
A.30°
B.36°
C.40°
D.45°
【解答】解:∵AB=AC,
∴∠B=∠C,
∵AB=BD,
∴∠BAD=∠BDA,
∵CD=AD,
∴∠C=∠CAD,
∵∠BAD+∠CAD+∠B+∠C=180°,
∴5∠B=180°,
∴∠B=36°
故选:B.
10.(2
分)下列各组二次根式中,能合并的两个二次根式是(
)
A.
和
B.
和
C.
和
D.
和
【解答】解:A、
,3
与
不能合并,故错误;
B、
,
与
能合并,正确;
C、
,
=|b|
,不能合并,故错误;
D、
与
不能合并,故错误;
故选:B.
11.(2
分)如图,在△ABC
中,AB=AC,∠A=30°,以
B
为圆心,BC
的长为半径圆弧,交
AC
于点
D,连接
BD,则∠ABD=(
)
A.30°
B.60°
C.45°
D.90°
【解答】解:∵在△ABC
中,AB=AC,∠A=30°,
∴∠ABC=∠ACB=75°,
又∵以
B
为圆心,BC
的长为半径圆弧,交
AC
于点
D,
∴∠DBC=2(90°﹣∠BDC)=2×(90°﹣75°)=30°,
又∵∠ABC=∠ABD+∠DBC,
∴∠ABD=75°﹣30°=45°,
故选:C.
12.(2
分)若
,则
b
的取值范围是(
)
A.b≥0
B.b≥3
C.b≤3
D.b>3
【解答】解:∵
,
∴3﹣b≥0,
∴b≤3.
故选:C.
13.(2
分)如图,已知∠AOB=60°,点
P
在边
OA
上,OP=12,点
M,N
在边
OB
上,PM=PN,若
MN=2,
则
OM=(
)
A.3
B.4
C.5
D.6
【解答】解:过
P
作
PD⊥OB,交
OB
于点
D,
在
Rt△OPD
中,cos60°==
,OP=12,
∴OD=6,
∵PM=PN,PD⊥MN,MN=2,
∴MD=ND=
MN=1,
∴OM=OD﹣MD=6﹣1=5.
故选:C.
14.(2
分)如图,△ABC
的顶点
A、B、C
在边长为
1
的正方形网格的格点上,BD⊥AC
于点
D.则
BD
的长为(
)
A.
B.
C.
D.
【解答】解:如图,由勾股定理得
AC==
.
∵
BC×2=
AC BD,即
×2×2=
×
BD
∴BD=
.
故选:C.
15.(2
分)如图,在四边形
ABCD
中,AB=CD,BA
和
CD
的延长线交于点
E,若点
P
使得
S△PAB=S
△PCD,则满足此条件的点
P(
)
有且只有
1
个
有且只有
2
个
组成∠E
的角平分线
组成∠E
的角平分线和外角平分线所在的直线(E
点除外)
【解答】解:作∠E
的平分线,
可得点
P
到
AB
和
CD
的距离相等,
因为
AB=CD,
所以此时点
P
满足
S△PAB=S△PCD.
组成∠E
的角平分线和外角平分线所在的直线(E
点除外)
故选:D.
16.(2
分)张华在一次数学活动中,利用“在面积一定的矩形中,正方形的周长最短”的结论,推导出“式子
x+(x>0)的最小值是
2”.其推导方法如下:在面积是
1
的矩形中设矩形的一边长为
x,则另一边长是,矩形的周长是
2(x+);当矩形成为正方形时,就有
x=(x>0),解得
x=1,这
时矩形的周长
2(x+)=4
最小,因此
x+
(x>0)的最小值是
2.模仿张华的推导,你求得式子
(x>0)的最小值是(
)
A.2
B.1
C.6
D.10
【解答】解:∵x>0,
∴在原式中分母分子同除以
x,
即
=x+
,
在面积是
9
的矩形中设矩形的一边长为
x,则另一边长是,
矩形的周长是
2(x+);
当矩形成为正方形时,就有
x=,(x>0),解得
x=3,
这时矩形的周长
2(x+)=12
最小,
因此
x+(x>0)的最小值是
6.
故选:C.
二、填空题:(本大题共
4
个小题,每小题
3
分,共
12
分.把答案写在题中横线上)
17.(3
分)已知:(a+6)2+=0,则
2b2﹣4b﹣a
的值为
12
.
【解答】解:∵(a+6)2+
=0,
∴a+6=0,b2﹣2b﹣3=0,
解得,a=﹣6,b2﹣2b=3,
可得
2b2﹣4b=6,
则
2b2﹣4b﹣a=6﹣(﹣6)=12,
故答案为:12.
18.(3
分)如图,Rt△ABC
中,AB=9,BC=6,∠B=90°,将△ABC
折叠,使
A
点与
BC
的中点
D
重合,折痕为
MN,则线段
BN
的长为
4
.
【解答】解:设
BN=x,由折叠的性质可得
DN=AN=9﹣x,
∵D
是
BC
的中点,
∴BD=3,
在
Rt△BND
中,x2+32=(9﹣x)2,
解得
x=4.
故线段
BN
的长为
4.
故答案为:4.
19.(3
分)如图,一只蚂蚁从点
A
沿数轴向右直爬
2
个单位到达点
B,点
A
表示﹣,设点
B
所表示的数为
m,则(m﹣1)(m﹣3)的值为
1
.
【解答】解:由题意得:m=﹣
+2,
(m﹣1)(m﹣3)
=(﹣+2﹣1)(﹣+2﹣3)
=(1﹣)(﹣1﹣)
=2﹣1
=1,
故答案为:1.
20.(3
分)下面是一个按某种规律排列的数表:
第
1
行
1
第
2
行
2
第
3
行
2
3
第
4
行
2
4
…
…
那么第
5
行中的第
2
个数是
3
,第
n(n>1,且
n
是整数)
行的第
2
个数
是
.(用含
n
的代数式表示)
【解答】解:第五行的第二个数是
,
第
n
行的第二个数的算术平方根是
,
故答案为:3
,
.
三、解答题:(本大题共
6
个小题,共
56
分.解答应写出文字说明、证明过程或演算步骤)
21.(8
分)当
a=
,求代数式
的值.
【解答】解:a=(+2)(2﹣)2+
=(2+)(2﹣)(2﹣)+
=1×(2﹣
)+
=2,
原式=
=
当
a=2
时,原式=2.
22.(9
分)在如图所示的方格纸中,每个小方格都是边长为
1
个单位的正方形,△ABC
的三个顶点都在格点上(每个小方格的顶点叫格点)
画出△ABC
关于直线
l
对称的图形△A1B1C1;
画出△ABC
关于点
O
中心对称的图形△A2B2C2,并标出点
M
的对称点
M′;
直接写出线段
MM′的长度.
【解答】解:(1)△A1B1C1如图所示;
(2)△A2B2C2
如图所示;
(3)MM′=
=2
.
23.(9
分)在本学期我们学习了角平分线的性质定理和判定定理,那么,你还是否记得它们的具体内容.
请把下面两个定理所缺的内容补充完整:
角平分线性质定理:角平分线上的点到
这个角的两边
的距离相等.
角平分线判定定理:到角的两边距离相等的点在
角平分线上
.
老师在黑板上画出了图形,把判定定理的已知、求证写在了黑板上,可是有些内容不完整,请你把内容补充完整
已知:如图
1,点
P
是∠AOB
内一点,PD⊥AO,PE⊥OB,垂足分别为
D、E,且
PD=
PE
,求证:
点
P
在∠AOB
的
平分线上
上
请你完成证明过程:
知识运用:如图
2,三条公路两两相交,现在要修建一加油站,使加油站到三条公路的距离相等,
加油站可选择的位置共有
4
处.
【解答】解:(1)角平分线性质定理:角平分线上的点到这个角的两边的距离相等.角平分线判定定理:到角的两边距离相等的点在角平分线上,
故答案为:这个角的两边;角平分线上;
已知:如图
1,点
P
是∠AOB
内一点,PD⊥AO,PE⊥OB,垂足分别为
D、E,且
PD=PE,求
证:点
P
在∠AOB
的平分线上.
故答案为:PE;平分线上;
如图:作射线
OP,
∵PD⊥AO,PE⊥OB,
∴∠PDO=∠PEO=90°,
在
Rt△OPD
和
Rt△OPE
中,
,
∴Rt△OPD≌Rt△OPE,
∴∠DOP=∠EOP,
∴OP
是∠AOB
的平分线,即点
P
在∠AOB
平分线上;
如图
2,M、N、G、H
即为所求,
故答案为:4.
24.(9
分)兴发服装店老板用
4500
元购进一批某款
T
恤衫,由于深受顾客喜爱,很快售完,老板又用
4950
元购进第二批该款式
T
恤衫,所购数量与第一批相同,但每件进价比第一批多了
9
元.
第一批该款式
T
恤衫每件进价是多少元?
老板以每件
120
元的价格销售该款式
T
恤衫,当第二批
T
恤衫售出时,出现了滞销,于是决定降价促销,若要使第二批的销售利润不低于
650
元,剩余的
T
恤衫每件售价至少要多少元?(利润=
售价﹣进价)
【解答】解:(1)设第一批
T
恤衫每件进价是
x
元,由题意,得
=
,
解得
x=90,
经检验
x=90
是分式方程的解,符合题意.
答:第一批
T
恤衫每件的进价是
90
元;
(2)设剩余的
T
恤衫每件售价
y
元.
由(1)知,第二批购进
=50(件).
由题意,得
120×50×+y×50×
﹣4950≥650,
解得
y≥80.
答:剩余的
T
恤衫每件售价至少要
80
元.
25.(10
分)在一平直河岸
l
同侧有
A,B
两个村庄,A,B
到
l
的距离分别是
3km
和
2km,AB=akm(a
>1).现计划在河岸
l
上建一抽水站
P,用输水管向两个村庄供水.
方案设计
某班数学兴趣小组设计了两种铺设管道方案:图
1
是方案一的示意图,设该方案中管道长度为
d1,且d1=PB+BA(km)(其中
BP⊥l
于点
P);图
2
是方案二的示意图,设该方案中管道长度为
d2,且
d2=
PA+PB(km)(其中点
A′与点
A
关于
l
对称,A′B
与
l
交于点
P).
观察计算
在方案一中,d1=
a+2
km(用含
a
的式子表示)
在方案二中,组长小宇为了计算
d2
的长,作了如图
3
所示的辅助线,请你按小宇同学的思路计算,d2=
km(用含
a
的式子表示).
探索归纳
(1)①当
a=4
时,比较大小:d1
<
d2(填“>”、“=”或“<”);
②当
a=6
时,比较大小:d1
>
d2(填“>”、“=”或“<”);
(2)请你参考方框中的方法指导,就
a(当
a>1
时)的所有取值情况进行分析,要使铺设的管道长度
较短,
应选择方案一还是方案二?
【解答】解:(1)∵如图
1,作
A
关于执行
l
的对称点
A′,连接
PA′,
∵A
和
A'关于直线
l
对称,
∴PA=PA',
d1=PB+BA=PB+PA'=a+2;
故答案为:a+2;
(2)
因
为
BK2=a2﹣1,
A'B2=BK2+A'K2=a2﹣1+52=a2+24
所以
d2=;
故答案为:
;
探索归纳:
(1)①当
a=4
时,d1=6,d2=,d1<d2;
②当
a=6
时,d1=8,d2=,d1>d2;
故答案为:<,>;
(2)d12﹣d22=(a+2)2﹣(
)2=4a﹣20.
①当
4a﹣20>0,即
a>5
时,d12﹣d22>0,
∴d1﹣d2>0,
∴d1>d2;
②当
4a﹣20=0,即
a=5
时,d12﹣d22=0,
∴d1﹣d2=0,
∴d1=d2
③当
4a﹣20<0,即
a<5
时,d12﹣d22<0,
∴d1﹣d2<0,
∴d1<d2
综上可知:当
a>5
时,选方案二;
当
a=5
时,选方案一或方案二;
当
1<a<5
时,选方案一.
26.(11
分)(1)如图(1),已知:在△ABC
中,∠BAC=90°,AB=AC,直线
m
经过点
A,BD⊥直线
m,CE⊥直线
m,垂足分别为点
D、E.
证明:DE=BD+CE.
如图(2),将(1)中的条件改为:在△ABC
中,AB=AC,D、A、E
三点都在直线
m
上,并且
有∠BDA=∠AEC=∠BAC=α,其中
α
为任意锐角或钝角.请问结论
DE=BD+CE
是否成立?如成立,
请你给出证明;若不成立,请说明理由.
拓展与应用:如图(3),D、E
是
D、A、E
三点所在直线
m
上的两动点(D、A、E
三点互不重合),点
F
为∠BAC
平分线上的一点,且△ABF
和△ACF
均为等边三角形,连接
BD、CE,若∠BDA=
∠AEC=∠BAC,试判断△DEF
的形状并说明理由.
【解答】解:(1)如图
1,∵BD⊥直线
m,CE⊥直线
m,
∴∠BDA=∠CEA=90°,
∵∠BAC=90°,
∴∠BAD+∠CAE=90°
∵∠BAD+∠ABD=90°,
∴∠CAE=∠ABD,
在△ADB
和△CEA
中,
,
∴△ADB≌△CEA(AAS),
∴AE=BD,AD=CE,
∴DE=AE+AD=BD+CE;
如图
2,∵∠BDA=∠BAC=α,
∴∠DBA+∠BAD=∠BAD+∠CAE=180°﹣α,
∴∠DBA=∠CAE,
在△ADB
和△CEA
中,
,
∴△ADB≌△CEA(AAS),
∴AE=BD,AD=CE,
∴DE=AE+AD=BD+CE;
如图
3,由(2)可知,△ADB≌△CEA,
∴BD=AE,∠DBA=∠CAE,
∵△ABF
和△ACF
均为等边三角形,
∴∠ABF=∠CAF=60°,BF=AF,
∴∠DBA+∠ABF=∠CAE+∠CAF,
∴∠DBF=∠FAE,
∵在△DBF
和△EAF
中,
,
∴△DBF≌△EAF(SAS),
∴DF=EF,∠BFD=∠AFE,
∴∠DFE=∠DFA+∠AFE=∠DFA+∠BFD=60°,
∴△DEF
为等边三角形.
同课章节目录
