沪教版八年级(上)期末数学模拟试卷1(word版、含解析)
文档属性
| 名称 | 沪教版八年级(上)期末数学模拟试卷1(word版、含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 262.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-06 09:42:50 | ||
图片预览




文档简介
沪教版八年级(上)期末数学模拟试卷
一、选择题(本大题共
6
小题,每小题
2
分,满分
12
分)【下列各题的四个选项中,有且只有一个选项是正确的,请选择正确项的代号并填在答题纸的相应位置上】
1.(2
分)下列二次根式中,与互为有理化因式的是(
)
A.
B.
C.
D.
2.(2
分)下列方程中是一元二次方程的是(
)
A.
﹣1=0
B.
=3x
C.x2=y
D.x2=0
3.(2
分)下列函数中,y
随着
x
的增大而减小的是(
)
A.y=3x
B.y=﹣3x
C.
D.
4.(2
分)下列命题中,真命题是(
)
A.当路程一定时,时间与速度成正比例
B.“全等三角形的面积相等”的逆命题是真命题
C.
是最简二次根式
D.到直线
AB
的距离等于
1
厘米的点的轨迹是平行于直线
AB
且和
AB
距离为
1cm
的一条直线
5.(2
分)某校八年级同学到距学校
6
千米的郊外春游,一部分同学步行,另一部分同学骑自行车,如图,l1、l2
分别表示步行和骑车的同学前往目的地所走的路程
y(千米)与所用时间
x(分钟)之间的函数图象,则以下判断错误的是(
)
骑车的同学比步行的同学晚出发
30
分钟
步行的速度是
6
千米/时
骑车的同学从出发到追上步行的同学用了
20
分钟
骑车的同学和步行的同学同时到达目的地
6.(2
分)如图,△ABC
中,P、Q
分别是
BC、AC
上的点,作
PR⊥AB
于点
R,PS⊥AC
于点
S,若
PR
=PS,则下列结论正确的个数是(
)
(1)PQ=PB;
(2)AS=AR;(3)△BRP≌△PSC
(4)∠C=∠SPC
A.1
个
B.2
个
C.3
个
D.4
个
二、填空题(本大题共
12
小题,每小题
2
分,满分
24
分)【请将结果直接填入答题纸的相应位置】
7.(2
分)+=
.
8.(2
分)方程
x2﹣24=0
的根是
.
9.(2
分)若在实数范围内有意义,则
x
的取值范围是
.
10.(2
分)如果正比例函数的图象经过点(2,),则正比例函数解析式是
.
11.(2
分)在实数范围内分解因式:x2﹣x﹣3=
.
12.(2
分)若关于
x
的一元二次方程
x2﹣(k﹣1)x+k=0
有一个根为﹣1,则
k=
.
13.(2
分)如果
f(x)=2x2﹣1,那么
f()=
.
14.(2
分)某印刷厂
3
月份印刷了
50
万册书籍,5
月份印刷了
72
万册书籍,如果每月印刷的增长率都为
x,则根据题意,可建立关于
x
的方程是
.
15.(2
分)已知如图,在
Rt△ABC
中,∠ACB=90°,CD
是斜边上的中线,若
CD=BC,则∠A=
.
16.(2
分)如图,在△ABC
中,EF
是
AC
的垂直平分线,AF=12,BF=3,则
BC=
.
17.(2
分)如果等腰三角形腰上的高是腰长的一半,那么它顶角的度数是
.
18.(2
分)如图,将等腰直角△ABC
绕底角顶点
A
逆时针旋转
15°后得到△A′B′C′,如果
AC=
,那么两个三角形的重叠部分面积为
.
三、简答题(本大题共
4
小题,每小题
6
分,满分
24
分)
19.(6
分)﹣
+(
+1)2
20.(6
分)计算:﹣
+(x>0,y>0)
21.(6
分)用配方法解方程:x2+5x﹣2=0
22.(6
分)已知关于
x
的一元二次方程(1﹣m2)x2+2(1﹣m)x﹣1=0
有两个实数根,求
m
的取值范围.
四、解答题(本大题共
4
小题,23
题
6
分,其余每题
8
分,满分
30
分)
23.(6
分)已知点
A(0,3)、B(﹣2,1)、C(2,1),试判断△ABC
的形状.
24.(8
分)已知:如图,点
D
是
BC
的中点,DE⊥AB,DF⊥AC,垂足分别为点
E、F,DE=DF.求证:AD⊥BC.
25.(8
分)已知:如图,∠ABC=∠ADC=90°,E、F
分别是
AC、BD
的中点.
求证:EF⊥BD;
若
AC=10cm,BD=8cm,求
EF
的长.
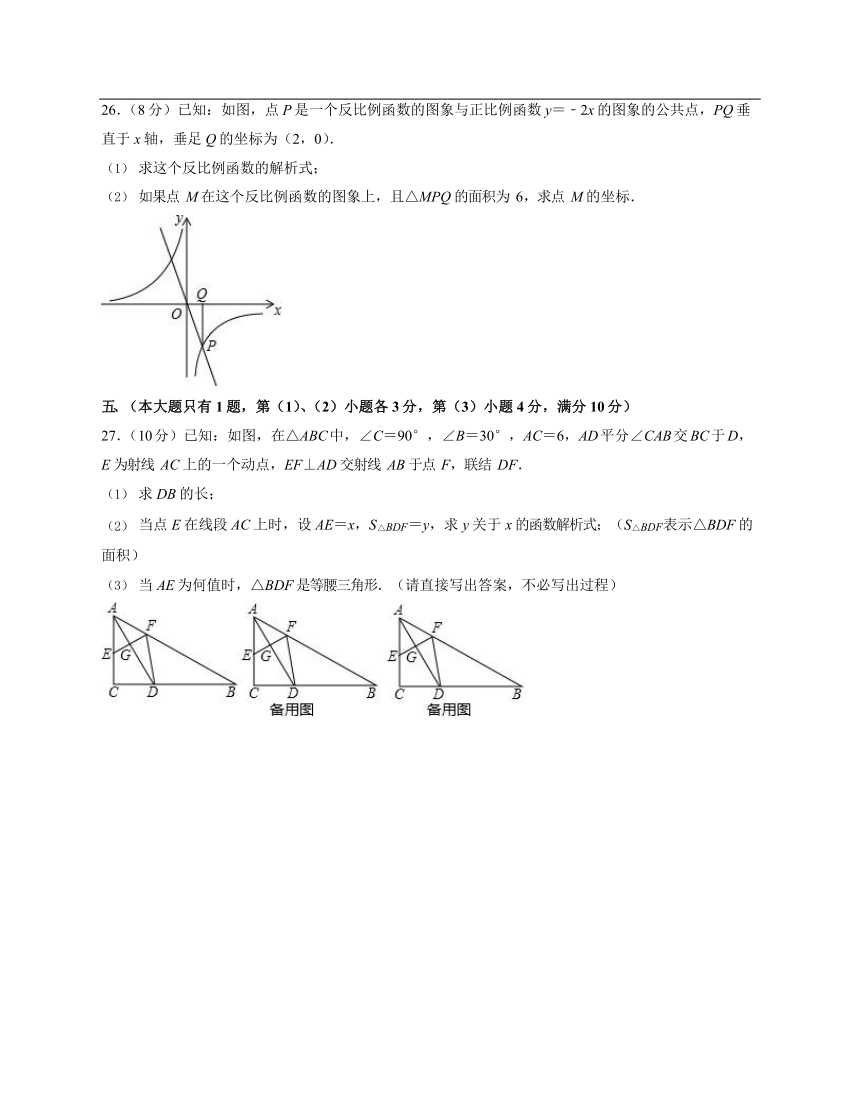
26.(8
分)已知:如图,点
P
是一个反比例函数的图象与正比例函数
y=﹣2x
的图象的公共点,PQ
垂直于
x
轴,垂足
Q
的坐标为(2,0).
求这个反比例函数的解析式;
如果点
M
在这个反比例函数的图象上,且△MPQ
的面积为
6,求点
M
的坐标.
五、(本大题只有
1
题,第(1)、(2)小题各
3
分,第(3)小题
4
分,满分
10
分)
27.(10
分)已知:如图,在△ABC
中,∠C=90°,∠B=30°,AC=6,AD
平分∠CAB
交BC
于D,
E
为射线
AC
上的一个动点,EF⊥AD
交射线
AB
于点
F,联结
DF.
求
DB
的长;
当点
E
在线段
AC
上时,设
AE=x,S△BDF=y,求
y
关于
x
的函数解析式;(S△BDF表示△BDF
的面积)
当
AE
为何值时,△BDF
是等腰三角形.(请直接写出答案,不必写出过程)
沪教版八年级(上)期末数学试卷
参考答案与试题解析
一、选择题(本大题共
6
小题,每小题
2
分,满分
12
分)【下列各题的四个选项中,有且只有一个选项是正确的,请选择正确项的代号并填在答题纸的相应位置上】
1.(2
分)下列二次根式中,与互为有理化因式的是(
)
A.
B.
C.
D.
【解答】解:与
互为有理化因式的是
.
故选:C.
2.(2
分)下列方程中是一元二次方程的是(
)
A.
﹣1=0
B.
=3x
C.x2=y
D.x2=0
【解答】解:A、
+
﹣1=0,是分式方程,不合题意;
B、
=3x,是无理方程,不合题意;
C、x2=y,是二元二次方程,不合题意;
D、x2=0,是一元二次方程,符合题意.
故选:D.
3.(2
分)下列函数中,y
随着
x
的增大而减小的是(
)
A.y=3x
B.y=﹣3x
C.
D.
【解答】解:A、y=3x,y
随着
x
的增大而增大,故此选项错误;
B、y=﹣3x,y
随着
x
的增大而减小,正确;
C、y=
,每个象限内,y
随着
x
的增大而减小,故此选项错误;
D、y=﹣
,每个象限内,y
随着
x
的增大而增大,故此选项错误;
故选:B.
4.(2
分)下列命题中,真命题是(
)
A.当路程一定时,时间与速度成正比例B.“全等三角形的面积相等”的逆命题是真命题
C.
是最简二次根式
D.到直线
AB
的距离等于
1
厘米的点的轨迹是平行于直线
AB
且和
AB
距离为
1cm
的一条直线
【解答】解:A、当路程一定时,时间与速度成反比例,故本选项错误;
B、“全等三角形的面积相等”的逆命题是面积相等的三角形全等,是假命题,故本选项错误;
C、
是最简二次根式,故本选项正确;
D、空间内与直线
AB
距离等于
1
厘米的点的轨迹是平行于直线
AB
且和
AB
距离为
1cm
的无数条直线,
故本选项错误;
故选:C.
5.(2
分)某校八年级同学到距学校
6
千米的郊外春游,一部分同学步行,另一部分同学骑自行车,如图,l1、l2
分别表示步行和骑车的同学前往目的地所走的路程
y(千米)与所用时间
x(分钟)之间的函数图象,则以下判断错误的是(
)
骑车的同学比步行的同学晚出发
30
分钟
步行的速度是
6
千米/时
骑车的同学从出发到追上步行的同学用了
20
分钟
骑车的同学和步行的同学同时到达目的地
【解答】解:骑车的同学比步行的同学晚出发
30
分钟,所以
A
正确;
步行的速度是
6÷1=6
千米/小时,所以
B
正确;
骑车的同学从出发到追上步行的同学用了
50﹣30=20
分钟,所以
C
正确;
骑车的同学用了
54﹣30=24
分钟到目的地,比步行的同学提前
6
分钟到达目的地,所以
D
错误;
故选:D.
6.(2
分)如图,△ABC
中,P、Q
分别是
BC、AC
上的点,作
PR⊥AB
于点
R,PS⊥AC
于点
S,若
PR
=PS,则下列结论正确的个数是(
)
(1)PQ=PB;
(2)AS=AR;(3)△BRP≌△PSC
(4)∠C=∠SPC
A.1
个
B.2
个
C.3
个
D.4
个
【解答】解:连接
AP,
∵PR⊥AB,PS⊥AC,PR=PS,
∴点
P
在∠A
的平分线上,∠ARP=∠ASP=90°,
∴∠SAP=∠RAP,
在
Rt△ARP
和Rt△ASP
中,,
∴Rt△ARP≌Rt△ASP,(HL),
∴AR=AS,∴②正确;
∵PR=PS,∠PRB=∠PSC=90°,
∴无法判断△BRP≌△PSC,故③错误;
∵∠PRB=∠PSQ=90°,PR=PS,
无法判断△BRP≌△PSQ,
∴PQ≠PB,故①错误;
∵△PSC
是直角三角形,不一定是等腰直角三角形,
∴∠C
与∠SPC
不一定相等,故④错误;
故选:A.
二、填空题(本大题共
12
小题,每小题
2
分,满分
24
分)【请将结果直接填入答题纸的相应位置】
7.(2
分)+=
3
.
【解答】解:
=2
+
=3
.
故答案为:3
.
8.(2
分)方程
x2﹣24=0
的根是
x1=2,x2=﹣2
.
【解答】解:x2﹣24=0,
则
x2=24,
故
x=±,
解得:x1=2
,x2=﹣2
.
故答案为:x1=2
,x2=﹣2
.
9.(2
分)若在实数范围内有意义,则
x
的取值范围是
x≥﹣2
.
【解答】解:由题意得,3x+6≥0,
解得:x≥﹣2.
故答案为:x≥﹣2.
10.(2
分)如果正比例函数的图象经过点(2,),则正比例函数解析式是
y=0.25x
.
【解答】解:设函数的解析式是
y=kx(k≠0),把(2,0.5)代入就得到:2k=0.5,
解得:k=0.25,
因而这个函数的解析式为:y=0.25x.
故答案为:y=0.25x
11.(2
分)在实数范围内分解因式:x2﹣x﹣3=
.
【解答】解:解方程
x2﹣x﹣3=0,
得
x=,
则:x2﹣x﹣3=
.
故答案是:
.
12.(2
分)若关于
x
的一元二次方程
x2﹣(k﹣1)x+k=0
有一个根为﹣1,则
k=
0
.
【解答】解:把
x=﹣1
代入方程
x2﹣(k﹣1)x+k=0
得
1+k﹣1+k=0,解得
k=0.
故答案为
0.
13.(2
分)如果
f(x)=2x2﹣1,那么
f()=
9
.
【解答】解:将
x=代入
f(x)=2x2﹣1
得:f(
)=2×5﹣1=9,
故答案为:9.
14.(2
分)某印刷厂
3
月份印刷了
50
万册书籍,5
月份印刷了
72
万册书籍,如果每月印刷的增长率都为
x,则根据题意,可建立关于
x
的方程是
50(1+x)2=72
.
【解答】解:设每月印刷的增长率都为
x,
根据题意得:50(1+x)2=72.
故答案为:50(1+x)2=72.
15.(2
分)已知如图,在
Rt△ABC
中,∠ACB=90°,CD
是斜边上的中线,若
CD=BC,则∠A=
30°
.
【解答】解:如图,∵在
Rt△ABC
中,∠ACB=90°,CD
是斜边上的中线,
∴BD=CD.
又∵CD=BC,
∴CD=BC=BD,
∴△BCD
是等边三角形,
∴∠B=60°,
∴∠A=90°﹣∠B=30°.
故答案是:30°.
16.(2
分)如图,在△ABC
中,EF
是
AC
的垂直平分线,AF=12,BF=3,则
BC=
15
.
【解答】解:∵EF
是线段
AC
的垂直平分线,
∴FC=AF=12,
∵BF=3,
∴BC=BF+FC=3+12=15,
故答案为:15.
17.(2
分)如果等腰三角形腰上的高是腰长的一半,那么它顶角的度数是
30°或
150°
.
【解答】解:①如图,△ABC
中,AB=AC,CD⊥AB
且
CD=
AB,
∵△ABC
中,CD⊥AB
且
CD=AB,AB=AC,
∴CD=
AC,
∴∠A=30°.
②如图,△ABC
中,AB=AC,CD⊥BA
的延长线于点
D,且
CD=AB,
∵∠CDA=90°,CD=
AB,AB=AC,
∴CD=
AC,
∴∠DAC=30°,
∴∠A=150°.
故答案为:30°或
150°.
18.(2
分)如图,将等腰直角△ABC
绕底角顶点
A
逆时针旋转
15°后得到△A′B′C′,如果
AC=
,那么两个三角形的重叠部分面积为
.
【解答】解:∵等腰直角△ABC
绕点
A
逆时针旋转
15°后得到△AB′C′,
∴∠CAC′=15°,
∴∠C′AB=∠CAB﹣∠CAC′=45°﹣15°=30°,AC′=AC=
,
∴阴影部分的面积=
×
×tan30°×
=
,
故答案为:
.
三、简答题(本大题共
4
小题,每小题
6
分,满分
24
分)
19.(6
分)﹣
+(
+1)2
【解答】解:原式=
=8+2
.
20.(6
分)计算:﹣
+(x>0,y>0)
【解答】解:原式=
﹣2
+3
=
.
21.(6
分)用配方法解方程:x2+5x﹣2=0
【解答】解:∵x2+5x﹣2=0,
∴x2+5x=2,
∴x2+5x+
=2+
,即(x+
)2=
,
则
x+=±
,
∴x=﹣
±
,
即
x1=﹣+
,x2=﹣
﹣
.
22.(6
分)已知关于
x
的一元二次方程(1﹣m2)x2+2(1﹣m)x﹣1=0
有两个实数根,求
m
的取值范围.
【解答】解:根据题意知,△=4(1﹣m)2﹣4(1﹣m2)×(﹣1)≥0,
解得:m≤1,
又∵1﹣m2≠0,
∴m≠±1,
则
m<1
且
m≠﹣1.
四、解答题(本大题共
4
小题,23
题
6
分,其余每题
8
分,满分
30
分)
23.(6
分)已知点
A(0,3)、B(﹣2,1)、C(2,1),试判断△ABC
的形状.
【解答】解:∵A(0,3)、B(﹣2,1)、C(2,1),
∴AB=2
,AC=2
,BC=4,
∴BC2=AB2+AC2,
∴∠BAC=90°,
∵AB=AC,
∴△ABC
是等腰直角三角形.
24.(8
分)已知:如图,点
D
是
BC
的中点,DE⊥AB,DF⊥AC,垂足分别为点
E、F,DE=DF.求证:AD⊥BC.
【解答】证明:∵点
D
是
BC
的中点,
∴BD=CD,
∵DE⊥AB,DF⊥AC,
∴△BDE
和△CDF
都是直角三角形,
在
Rt△BDE
和Rt△CDF
中,
∴Rt△BDE≌Rt△CDF(HL),
∴∠B=∠C(全等三角形的对应角相等).
∴AB=AC
(等角对等边).
∵AB=AC,点
D
是
BC
的中点,
∴AD⊥BC
(等腰三角形的三线合一).
25.(8
分)已知:如图,∠ABC=∠ADC=90°,E、F
分别是
AC、BD
的中点.
求证:EF⊥BD;
若
AC=10cm,BD=8cm,求
EF
的长.
【解答】(1)证明:连接
EB,ED,
∵∠ABC=∠ADC=90°,E
是
AC
的中点,
∴BE=
AC,DE=
AC,
∴EB=ED,又
F
是
BD
的中点,
∴EF⊥BD;
(2)BE=
AC=5,BF=
BD=4,
由勾股定理得,EF==3(cm).
26.(8
分)已知:如图,点
P
是一个反比例函数的图象与正比例函数
y=﹣2x
的图象的公共点,PQ
垂直于
x
轴,垂足
Q
的坐标为(2,0).
求这个反比例函数的解析式;
如果点
M
在这个反比例函数的图象上,且△MPQ
的面积为
6,求点
M
的坐标.
【解答】解:(1)把
x=2
代入
y=﹣2x
得
y=﹣4
∴P(2,﹣4),
设反比例函数解析式
y=(k≠0),
∵P
在此图象上
∴k=2×(﹣4)=﹣8,
∴y=﹣
;
(2)∵P(2,﹣4),Q(2,0)
∴PQ=4,过
M
作
MN⊥PQ
于
N.
则
PQ MN=6,
∴MN=3,
设
M(x,﹣),
则
x=2+3=5
或
x=2﹣3=﹣1
当
x=5
时,﹣=﹣
,
当
x=﹣1
时,﹣=1,
∴M(5,﹣
)或(﹣1,8).
五、(本大题只有
1
题,第(1)、(2)小题各
3
分,第(3)小题
4
分,满分
10
分)
27.(10
分)已知:如图,在△ABC
中,∠C=90°,∠B=30°,AC=6,AD
平分∠CAB
交BC
于D,
E
为射线
AC
上的一个动点,EF⊥AD
交射线
AB
于点
F,联结
DF.
求
DB
的长;
当点
E
在线段
AC
上时,设
AE=x,S△BDF=y,求
y
关于
x
的函数解析式;(S△BDF表示△BDF
的面积)
当
AE
为何值时,△BDF
是等腰三角形.(请直接写出答案,不必写出过程)
【解答】解:(1)在
Rt△ABC
中,∵∠C=90°,∠B=30°,AC=6,
∴∠CAB=60°,AB=2AC=12,BC=
AC=6
,
∵AD
平分∠CAB
交
BC
于
D,
∴∠CAD=
∠CAB=30°,
∴CD=AC tan30°=2
,
∴BC=BC﹣CD=6
﹣2
=4
.
如图
1
中,作
DH⊥AB
于
H.
∵DA
平分∠CAB,DC⊥AC,DH⊥AB,
∴DC=DH=2
,
∵EF⊥AD,
∴∠AGE=∠AGF=90°,
∵∠EAG=∠FAG,∠AEG+∠EAG=90°,∠AFG+∠FAG=90°,
∴∠AEG=∠AFG,
∴AE=AF=x,
∴BF=12﹣x,
∴S△BDF= BF DH=(12﹣x) 2
=﹣
x+12
(0≤x≤6).
①当点
E
与
A
重合时,△BDF
是等腰三角形,此时
x=0,即
AE=0.
②如图
2
中,当
BD=BF
时,
∵BD=4
,
∴BF=4
,
∴AE=AF=AB﹣BF=12﹣4
,
③如图
2
中,当
BF=时,
∴AE=AF′=AB+BF′=12+4
,
④当
E,F,D
共线时,△BDF
是等腰三角形,此时
AE=8,
综上所述,当
AE
的值为
0
或
8
或
12﹣4或
12+4
时,△BDF
是等腰三角形.
一、选择题(本大题共
6
小题,每小题
2
分,满分
12
分)【下列各题的四个选项中,有且只有一个选项是正确的,请选择正确项的代号并填在答题纸的相应位置上】
1.(2
分)下列二次根式中,与互为有理化因式的是(
)
A.
B.
C.
D.
2.(2
分)下列方程中是一元二次方程的是(
)
A.
﹣1=0
B.
=3x
C.x2=y
D.x2=0
3.(2
分)下列函数中,y
随着
x
的增大而减小的是(
)
A.y=3x
B.y=﹣3x
C.
D.
4.(2
分)下列命题中,真命题是(
)
A.当路程一定时,时间与速度成正比例
B.“全等三角形的面积相等”的逆命题是真命题
C.
是最简二次根式
D.到直线
AB
的距离等于
1
厘米的点的轨迹是平行于直线
AB
且和
AB
距离为
1cm
的一条直线
5.(2
分)某校八年级同学到距学校
6
千米的郊外春游,一部分同学步行,另一部分同学骑自行车,如图,l1、l2
分别表示步行和骑车的同学前往目的地所走的路程
y(千米)与所用时间
x(分钟)之间的函数图象,则以下判断错误的是(
)
骑车的同学比步行的同学晚出发
30
分钟
步行的速度是
6
千米/时
骑车的同学从出发到追上步行的同学用了
20
分钟
骑车的同学和步行的同学同时到达目的地
6.(2
分)如图,△ABC
中,P、Q
分别是
BC、AC
上的点,作
PR⊥AB
于点
R,PS⊥AC
于点
S,若
PR
=PS,则下列结论正确的个数是(
)
(1)PQ=PB;
(2)AS=AR;(3)△BRP≌△PSC
(4)∠C=∠SPC
A.1
个
B.2
个
C.3
个
D.4
个
二、填空题(本大题共
12
小题,每小题
2
分,满分
24
分)【请将结果直接填入答题纸的相应位置】
7.(2
分)+=
.
8.(2
分)方程
x2﹣24=0
的根是
.
9.(2
分)若在实数范围内有意义,则
x
的取值范围是
.
10.(2
分)如果正比例函数的图象经过点(2,),则正比例函数解析式是
.
11.(2
分)在实数范围内分解因式:x2﹣x﹣3=
.
12.(2
分)若关于
x
的一元二次方程
x2﹣(k﹣1)x+k=0
有一个根为﹣1,则
k=
.
13.(2
分)如果
f(x)=2x2﹣1,那么
f()=
.
14.(2
分)某印刷厂
3
月份印刷了
50
万册书籍,5
月份印刷了
72
万册书籍,如果每月印刷的增长率都为
x,则根据题意,可建立关于
x
的方程是
.
15.(2
分)已知如图,在
Rt△ABC
中,∠ACB=90°,CD
是斜边上的中线,若
CD=BC,则∠A=
.
16.(2
分)如图,在△ABC
中,EF
是
AC
的垂直平分线,AF=12,BF=3,则
BC=
.
17.(2
分)如果等腰三角形腰上的高是腰长的一半,那么它顶角的度数是
.
18.(2
分)如图,将等腰直角△ABC
绕底角顶点
A
逆时针旋转
15°后得到△A′B′C′,如果
AC=
,那么两个三角形的重叠部分面积为
.
三、简答题(本大题共
4
小题,每小题
6
分,满分
24
分)
19.(6
分)﹣
+(
+1)2
20.(6
分)计算:﹣
+(x>0,y>0)
21.(6
分)用配方法解方程:x2+5x﹣2=0
22.(6
分)已知关于
x
的一元二次方程(1﹣m2)x2+2(1﹣m)x﹣1=0
有两个实数根,求
m
的取值范围.
四、解答题(本大题共
4
小题,23
题
6
分,其余每题
8
分,满分
30
分)
23.(6
分)已知点
A(0,3)、B(﹣2,1)、C(2,1),试判断△ABC
的形状.
24.(8
分)已知:如图,点
D
是
BC
的中点,DE⊥AB,DF⊥AC,垂足分别为点
E、F,DE=DF.求证:AD⊥BC.
25.(8
分)已知:如图,∠ABC=∠ADC=90°,E、F
分别是
AC、BD
的中点.
求证:EF⊥BD;
若
AC=10cm,BD=8cm,求
EF
的长.
26.(8
分)已知:如图,点
P
是一个反比例函数的图象与正比例函数
y=﹣2x
的图象的公共点,PQ
垂直于
x
轴,垂足
Q
的坐标为(2,0).
求这个反比例函数的解析式;
如果点
M
在这个反比例函数的图象上,且△MPQ
的面积为
6,求点
M
的坐标.
五、(本大题只有
1
题,第(1)、(2)小题各
3
分,第(3)小题
4
分,满分
10
分)
27.(10
分)已知:如图,在△ABC
中,∠C=90°,∠B=30°,AC=6,AD
平分∠CAB
交BC
于D,
E
为射线
AC
上的一个动点,EF⊥AD
交射线
AB
于点
F,联结
DF.
求
DB
的长;
当点
E
在线段
AC
上时,设
AE=x,S△BDF=y,求
y
关于
x
的函数解析式;(S△BDF表示△BDF
的面积)
当
AE
为何值时,△BDF
是等腰三角形.(请直接写出答案,不必写出过程)
沪教版八年级(上)期末数学试卷
参考答案与试题解析
一、选择题(本大题共
6
小题,每小题
2
分,满分
12
分)【下列各题的四个选项中,有且只有一个选项是正确的,请选择正确项的代号并填在答题纸的相应位置上】
1.(2
分)下列二次根式中,与互为有理化因式的是(
)
A.
B.
C.
D.
【解答】解:与
互为有理化因式的是
.
故选:C.
2.(2
分)下列方程中是一元二次方程的是(
)
A.
﹣1=0
B.
=3x
C.x2=y
D.x2=0
【解答】解:A、
+
﹣1=0,是分式方程,不合题意;
B、
=3x,是无理方程,不合题意;
C、x2=y,是二元二次方程,不合题意;
D、x2=0,是一元二次方程,符合题意.
故选:D.
3.(2
分)下列函数中,y
随着
x
的增大而减小的是(
)
A.y=3x
B.y=﹣3x
C.
D.
【解答】解:A、y=3x,y
随着
x
的增大而增大,故此选项错误;
B、y=﹣3x,y
随着
x
的增大而减小,正确;
C、y=
,每个象限内,y
随着
x
的增大而减小,故此选项错误;
D、y=﹣
,每个象限内,y
随着
x
的增大而增大,故此选项错误;
故选:B.
4.(2
分)下列命题中,真命题是(
)
A.当路程一定时,时间与速度成正比例B.“全等三角形的面积相等”的逆命题是真命题
C.
是最简二次根式
D.到直线
AB
的距离等于
1
厘米的点的轨迹是平行于直线
AB
且和
AB
距离为
1cm
的一条直线
【解答】解:A、当路程一定时,时间与速度成反比例,故本选项错误;
B、“全等三角形的面积相等”的逆命题是面积相等的三角形全等,是假命题,故本选项错误;
C、
是最简二次根式,故本选项正确;
D、空间内与直线
AB
距离等于
1
厘米的点的轨迹是平行于直线
AB
且和
AB
距离为
1cm
的无数条直线,
故本选项错误;
故选:C.
5.(2
分)某校八年级同学到距学校
6
千米的郊外春游,一部分同学步行,另一部分同学骑自行车,如图,l1、l2
分别表示步行和骑车的同学前往目的地所走的路程
y(千米)与所用时间
x(分钟)之间的函数图象,则以下判断错误的是(
)
骑车的同学比步行的同学晚出发
30
分钟
步行的速度是
6
千米/时
骑车的同学从出发到追上步行的同学用了
20
分钟
骑车的同学和步行的同学同时到达目的地
【解答】解:骑车的同学比步行的同学晚出发
30
分钟,所以
A
正确;
步行的速度是
6÷1=6
千米/小时,所以
B
正确;
骑车的同学从出发到追上步行的同学用了
50﹣30=20
分钟,所以
C
正确;
骑车的同学用了
54﹣30=24
分钟到目的地,比步行的同学提前
6
分钟到达目的地,所以
D
错误;
故选:D.
6.(2
分)如图,△ABC
中,P、Q
分别是
BC、AC
上的点,作
PR⊥AB
于点
R,PS⊥AC
于点
S,若
PR
=PS,则下列结论正确的个数是(
)
(1)PQ=PB;
(2)AS=AR;(3)△BRP≌△PSC
(4)∠C=∠SPC
A.1
个
B.2
个
C.3
个
D.4
个
【解答】解:连接
AP,
∵PR⊥AB,PS⊥AC,PR=PS,
∴点
P
在∠A
的平分线上,∠ARP=∠ASP=90°,
∴∠SAP=∠RAP,
在
Rt△ARP
和Rt△ASP
中,,
∴Rt△ARP≌Rt△ASP,(HL),
∴AR=AS,∴②正确;
∵PR=PS,∠PRB=∠PSC=90°,
∴无法判断△BRP≌△PSC,故③错误;
∵∠PRB=∠PSQ=90°,PR=PS,
无法判断△BRP≌△PSQ,
∴PQ≠PB,故①错误;
∵△PSC
是直角三角形,不一定是等腰直角三角形,
∴∠C
与∠SPC
不一定相等,故④错误;
故选:A.
二、填空题(本大题共
12
小题,每小题
2
分,满分
24
分)【请将结果直接填入答题纸的相应位置】
7.(2
分)+=
3
.
【解答】解:
=2
+
=3
.
故答案为:3
.
8.(2
分)方程
x2﹣24=0
的根是
x1=2,x2=﹣2
.
【解答】解:x2﹣24=0,
则
x2=24,
故
x=±,
解得:x1=2
,x2=﹣2
.
故答案为:x1=2
,x2=﹣2
.
9.(2
分)若在实数范围内有意义,则
x
的取值范围是
x≥﹣2
.
【解答】解:由题意得,3x+6≥0,
解得:x≥﹣2.
故答案为:x≥﹣2.
10.(2
分)如果正比例函数的图象经过点(2,),则正比例函数解析式是
y=0.25x
.
【解答】解:设函数的解析式是
y=kx(k≠0),把(2,0.5)代入就得到:2k=0.5,
解得:k=0.25,
因而这个函数的解析式为:y=0.25x.
故答案为:y=0.25x
11.(2
分)在实数范围内分解因式:x2﹣x﹣3=
.
【解答】解:解方程
x2﹣x﹣3=0,
得
x=,
则:x2﹣x﹣3=
.
故答案是:
.
12.(2
分)若关于
x
的一元二次方程
x2﹣(k﹣1)x+k=0
有一个根为﹣1,则
k=
0
.
【解答】解:把
x=﹣1
代入方程
x2﹣(k﹣1)x+k=0
得
1+k﹣1+k=0,解得
k=0.
故答案为
0.
13.(2
分)如果
f(x)=2x2﹣1,那么
f()=
9
.
【解答】解:将
x=代入
f(x)=2x2﹣1
得:f(
)=2×5﹣1=9,
故答案为:9.
14.(2
分)某印刷厂
3
月份印刷了
50
万册书籍,5
月份印刷了
72
万册书籍,如果每月印刷的增长率都为
x,则根据题意,可建立关于
x
的方程是
50(1+x)2=72
.
【解答】解:设每月印刷的增长率都为
x,
根据题意得:50(1+x)2=72.
故答案为:50(1+x)2=72.
15.(2
分)已知如图,在
Rt△ABC
中,∠ACB=90°,CD
是斜边上的中线,若
CD=BC,则∠A=
30°
.
【解答】解:如图,∵在
Rt△ABC
中,∠ACB=90°,CD
是斜边上的中线,
∴BD=CD.
又∵CD=BC,
∴CD=BC=BD,
∴△BCD
是等边三角形,
∴∠B=60°,
∴∠A=90°﹣∠B=30°.
故答案是:30°.
16.(2
分)如图,在△ABC
中,EF
是
AC
的垂直平分线,AF=12,BF=3,则
BC=
15
.
【解答】解:∵EF
是线段
AC
的垂直平分线,
∴FC=AF=12,
∵BF=3,
∴BC=BF+FC=3+12=15,
故答案为:15.
17.(2
分)如果等腰三角形腰上的高是腰长的一半,那么它顶角的度数是
30°或
150°
.
【解答】解:①如图,△ABC
中,AB=AC,CD⊥AB
且
CD=
AB,
∵△ABC
中,CD⊥AB
且
CD=AB,AB=AC,
∴CD=
AC,
∴∠A=30°.
②如图,△ABC
中,AB=AC,CD⊥BA
的延长线于点
D,且
CD=AB,
∵∠CDA=90°,CD=
AB,AB=AC,
∴CD=
AC,
∴∠DAC=30°,
∴∠A=150°.
故答案为:30°或
150°.
18.(2
分)如图,将等腰直角△ABC
绕底角顶点
A
逆时针旋转
15°后得到△A′B′C′,如果
AC=
,那么两个三角形的重叠部分面积为
.
【解答】解:∵等腰直角△ABC
绕点
A
逆时针旋转
15°后得到△AB′C′,
∴∠CAC′=15°,
∴∠C′AB=∠CAB﹣∠CAC′=45°﹣15°=30°,AC′=AC=
,
∴阴影部分的面积=
×
×tan30°×
=
,
故答案为:
.
三、简答题(本大题共
4
小题,每小题
6
分,满分
24
分)
19.(6
分)﹣
+(
+1)2
【解答】解:原式=
=8+2
.
20.(6
分)计算:﹣
+(x>0,y>0)
【解答】解:原式=
﹣2
+3
=
.
21.(6
分)用配方法解方程:x2+5x﹣2=0
【解答】解:∵x2+5x﹣2=0,
∴x2+5x=2,
∴x2+5x+
=2+
,即(x+
)2=
,
则
x+=±
,
∴x=﹣
±
,
即
x1=﹣+
,x2=﹣
﹣
.
22.(6
分)已知关于
x
的一元二次方程(1﹣m2)x2+2(1﹣m)x﹣1=0
有两个实数根,求
m
的取值范围.
【解答】解:根据题意知,△=4(1﹣m)2﹣4(1﹣m2)×(﹣1)≥0,
解得:m≤1,
又∵1﹣m2≠0,
∴m≠±1,
则
m<1
且
m≠﹣1.
四、解答题(本大题共
4
小题,23
题
6
分,其余每题
8
分,满分
30
分)
23.(6
分)已知点
A(0,3)、B(﹣2,1)、C(2,1),试判断△ABC
的形状.
【解答】解:∵A(0,3)、B(﹣2,1)、C(2,1),
∴AB=2
,AC=2
,BC=4,
∴BC2=AB2+AC2,
∴∠BAC=90°,
∵AB=AC,
∴△ABC
是等腰直角三角形.
24.(8
分)已知:如图,点
D
是
BC
的中点,DE⊥AB,DF⊥AC,垂足分别为点
E、F,DE=DF.求证:AD⊥BC.
【解答】证明:∵点
D
是
BC
的中点,
∴BD=CD,
∵DE⊥AB,DF⊥AC,
∴△BDE
和△CDF
都是直角三角形,
在
Rt△BDE
和Rt△CDF
中,
∴Rt△BDE≌Rt△CDF(HL),
∴∠B=∠C(全等三角形的对应角相等).
∴AB=AC
(等角对等边).
∵AB=AC,点
D
是
BC
的中点,
∴AD⊥BC
(等腰三角形的三线合一).
25.(8
分)已知:如图,∠ABC=∠ADC=90°,E、F
分别是
AC、BD
的中点.
求证:EF⊥BD;
若
AC=10cm,BD=8cm,求
EF
的长.
【解答】(1)证明:连接
EB,ED,
∵∠ABC=∠ADC=90°,E
是
AC
的中点,
∴BE=
AC,DE=
AC,
∴EB=ED,又
F
是
BD
的中点,
∴EF⊥BD;
(2)BE=
AC=5,BF=
BD=4,
由勾股定理得,EF==3(cm).
26.(8
分)已知:如图,点
P
是一个反比例函数的图象与正比例函数
y=﹣2x
的图象的公共点,PQ
垂直于
x
轴,垂足
Q
的坐标为(2,0).
求这个反比例函数的解析式;
如果点
M
在这个反比例函数的图象上,且△MPQ
的面积为
6,求点
M
的坐标.
【解答】解:(1)把
x=2
代入
y=﹣2x
得
y=﹣4
∴P(2,﹣4),
设反比例函数解析式
y=(k≠0),
∵P
在此图象上
∴k=2×(﹣4)=﹣8,
∴y=﹣
;
(2)∵P(2,﹣4),Q(2,0)
∴PQ=4,过
M
作
MN⊥PQ
于
N.
则
PQ MN=6,
∴MN=3,
设
M(x,﹣),
则
x=2+3=5
或
x=2﹣3=﹣1
当
x=5
时,﹣=﹣
,
当
x=﹣1
时,﹣=1,
∴M(5,﹣
)或(﹣1,8).
五、(本大题只有
1
题,第(1)、(2)小题各
3
分,第(3)小题
4
分,满分
10
分)
27.(10
分)已知:如图,在△ABC
中,∠C=90°,∠B=30°,AC=6,AD
平分∠CAB
交BC
于D,
E
为射线
AC
上的一个动点,EF⊥AD
交射线
AB
于点
F,联结
DF.
求
DB
的长;
当点
E
在线段
AC
上时,设
AE=x,S△BDF=y,求
y
关于
x
的函数解析式;(S△BDF表示△BDF
的面积)
当
AE
为何值时,△BDF
是等腰三角形.(请直接写出答案,不必写出过程)
【解答】解:(1)在
Rt△ABC
中,∵∠C=90°,∠B=30°,AC=6,
∴∠CAB=60°,AB=2AC=12,BC=
AC=6
,
∵AD
平分∠CAB
交
BC
于
D,
∴∠CAD=
∠CAB=30°,
∴CD=AC tan30°=2
,
∴BC=BC﹣CD=6
﹣2
=4
.
如图
1
中,作
DH⊥AB
于
H.
∵DA
平分∠CAB,DC⊥AC,DH⊥AB,
∴DC=DH=2
,
∵EF⊥AD,
∴∠AGE=∠AGF=90°,
∵∠EAG=∠FAG,∠AEG+∠EAG=90°,∠AFG+∠FAG=90°,
∴∠AEG=∠AFG,
∴AE=AF=x,
∴BF=12﹣x,
∴S△BDF= BF DH=(12﹣x) 2
=﹣
x+12
(0≤x≤6).
①当点
E
与
A
重合时,△BDF
是等腰三角形,此时
x=0,即
AE=0.
②如图
2
中,当
BD=BF
时,
∵BD=4
,
∴BF=4
,
∴AE=AF=AB﹣BF=12﹣4
,
③如图
2
中,当
BF=时,
∴AE=AF′=AB+BF′=12+4
,
④当
E,F,D
共线时,△BDF
是等腰三角形,此时
AE=8,
综上所述,当
AE
的值为
0
或
8
或
12﹣4或
12+4
时,△BDF
是等腰三角形.
同课章节目录
