2021-2022学年华东师大版数学九年级下册27.4 正多边形和圆课件(25张PPT)
文档属性
| 名称 | 2021-2022学年华东师大版数学九年级下册27.4 正多边形和圆课件(25张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-06 12:25:24 | ||
图片预览


文档简介
(共25张PPT)
27.4
正多边形和圆
华东师大·九年级下册
新课导入
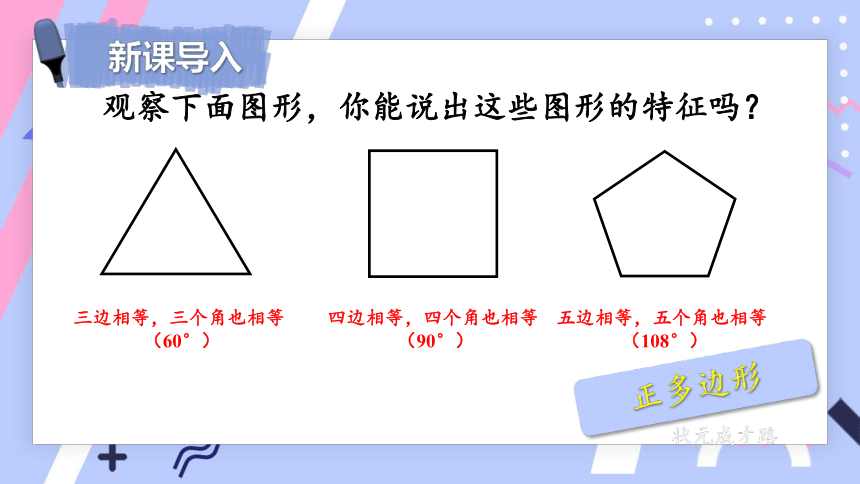
观察下面图形,你能说出这些图形的特征吗?
三边相等,三个角也相等
(60°)
四边相等,四个角也相等
(90°)
五边相等,五个角也相等
(108°)
正多边形
新课导入
想一想:
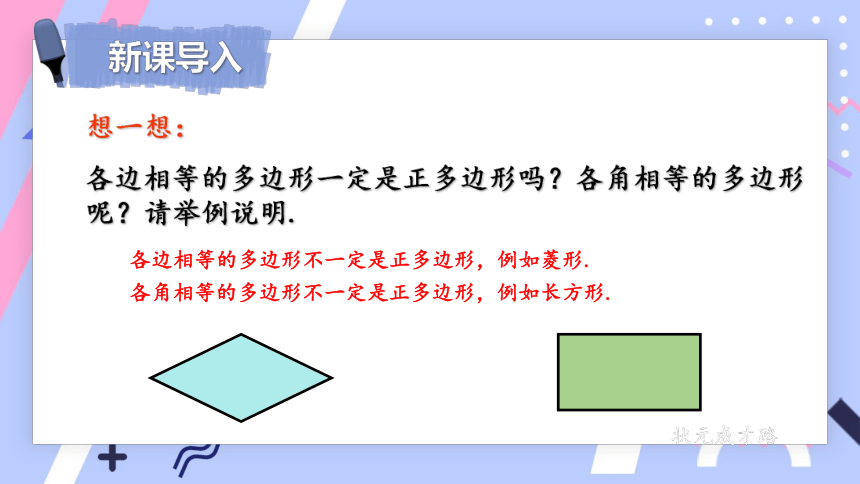
各边相等的多边形一定是正多边形吗?各角相等的多边形呢?请举例说明.
各边相等的多边形不一定是正多边形,例如菱形.
各角相等的多边形不一定是正多边形,例如长方形.
我们已经知道,各条边相等、各个角也相等的多边形是
正多边形.等边三角形是正三角形,正方形是正四边形.正
多边形都是轴对称图形,在日常生活和美术设计中都很常见.
推进新课
外接圆和内切圆
知识点1
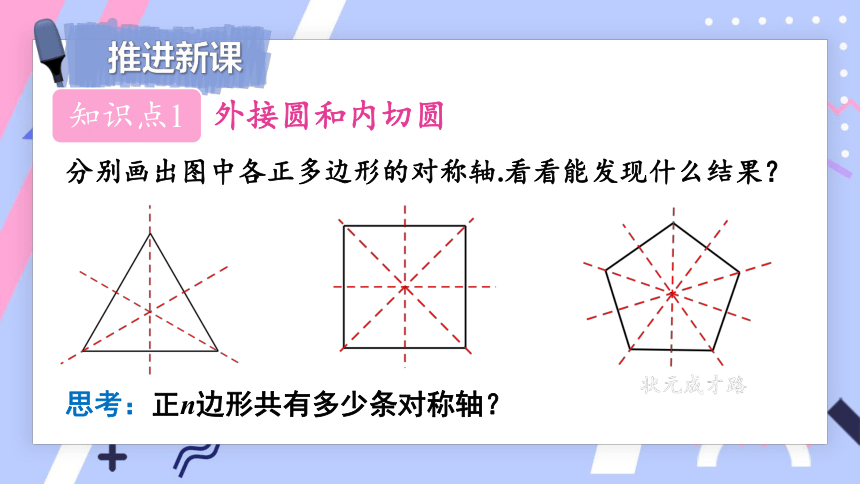
分别画出图中各正多边形的对称轴.看看能发现什么结果?
思考:正n边形共有多少条对称轴?
推进新课
A
B
C
D
E
F
G
H
I
J
O
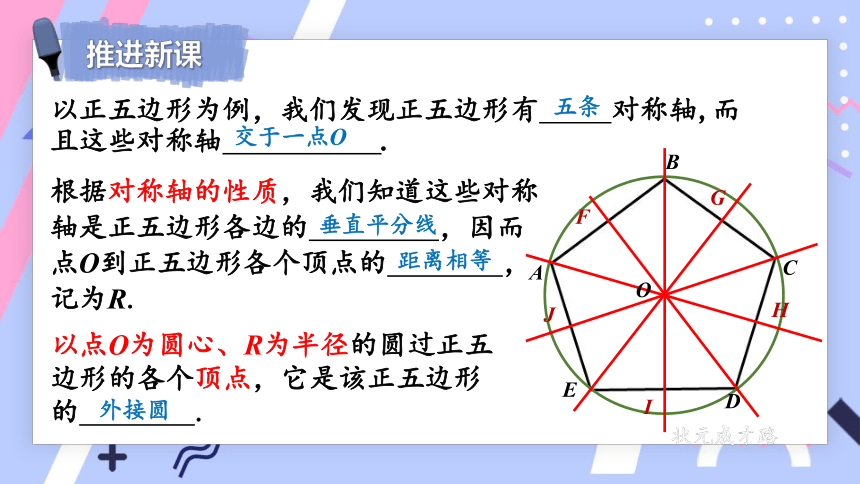
以正五边形为例,我们发现正五边形有
对称轴,而且这些对称轴
.
根据对称轴的性质,我们知道这些对称轴是正五边形各边的
,因而点O到正五边形各个顶点的
,记为R.
以点O为圆心、R为半径的圆过正五边形的各个顶点,它是该正五边形的
.
五条
交于一点O
垂直平分线
距离相等
外接圆
推进新课
A
B
C
D
E
F
G
H
I
J
O
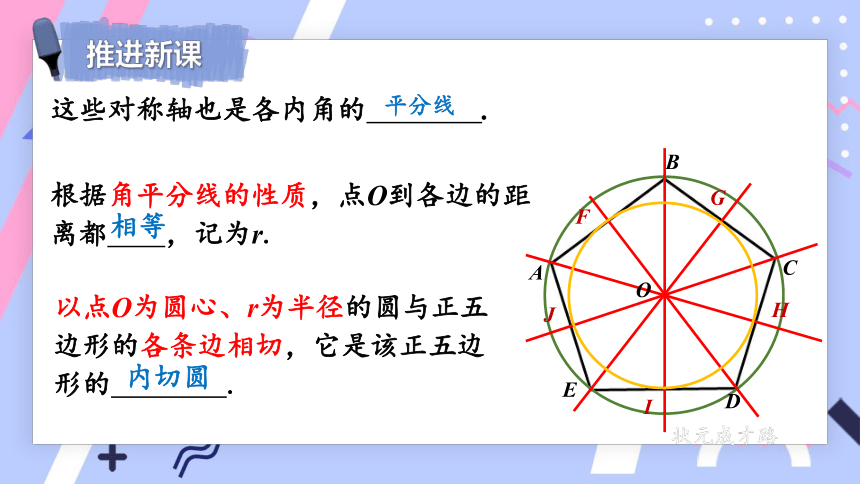
这些对称轴也是各内角的
.
根据角平分线的性质,点O到各边的距离都
,记为r.
相等
以点O为圆心、r为半径的圆与正五边形的各条边相切,它是该正五边形的
.
内切圆
平分线
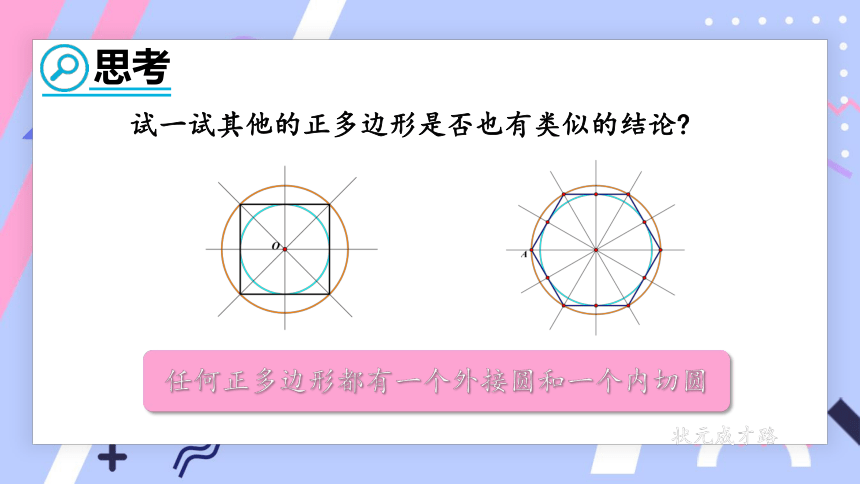
思考
试一试其他的正多边形是否也有类似的结论
任何正多边形都有一个外接圆和一个内切圆
.
.
O
中心角
半径R
边心距r
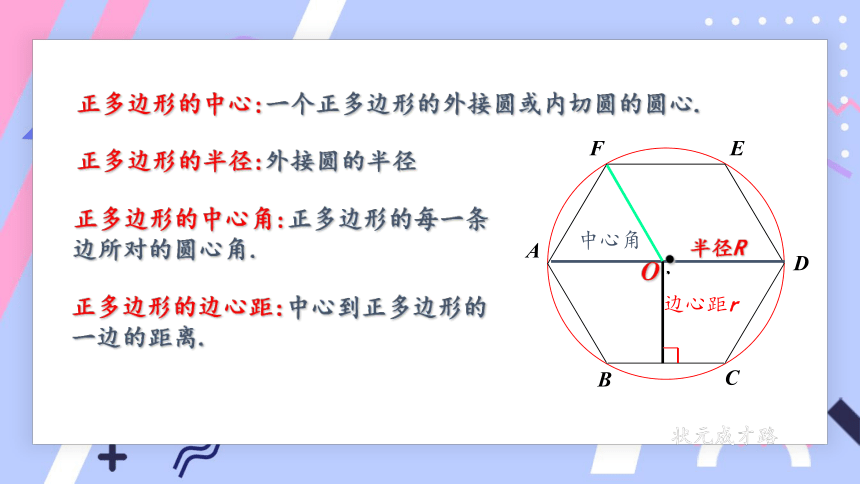
正多边形的中心:一个正多边形的外接圆或内切圆的圆心.
正多边形的半径:外接圆的半径
正多边形的中心角:正多边形的每一条边所对的圆心角.
正多边形的边心距:中心到正多边形的一边的距离.
A
B
C
D
E
F
O
中心角
边心距把△BOC分成2个
的直角三角形.
A
B
C
D
E
F
全等
.
练习
如果正n边形的中心角等于24°,求这个正多边形的边数.
解:由题意得:
24×n=360
n=15
这个正多边形的边数为15.
如图,在⊙O中,
,那么弦AB、BC、CD、DE、EA之间有什么关系?∠A、∠B、∠C、∠D、∠E之间又有什么关系?
在同一个圆中,等弧对等弦,
因此AB=BC=CD=DE=EA,
而根据圆周角定理,有∠A=∠B=∠C=∠D=∠E,
因此五边形ABCDE是正五边形.
正多边形的画法
知识点2
这样我们就得到下面正多边形与圆的关系:
把圆分成n(n>2)等份,依次连结各分点所得的多边形是这个圆的一个内接正n边形.
例
利用尺规作图,作出已知圆的内接正方形和内接正六边形.
解:内接正方形的做法:
(1)用直尺任作圆的一条直径AC;
(2)作与直径AC垂直的直径BD;
(3)顺次连结所得的圆上四点,则四边形ABCD即为所求作的正方形.
内接正六边形的作法:
(1)用直尺任作圆的一条直径AD;
(2)以点A为圆心、OA为半径作圆,与⊙O交于点B、F;
(3)以点D为圆心、OD为半径作圆,与⊙O交于点C、E;
(4)顺次连结所得的圆上六点,则六边形ABCDEF即为所求作的正六边形.
例
利用尺规作图,作出已知圆的内接正方形和内接正六边形.
内接正六边形的做法:
(1)任意作圆的一条半径OA;
(2)沿半径OA用量角器量出正六边形中心角的度数(60°),与⊙O交于点B;
(3)依次量出C、D、E、F
;
(4)顺次连结所得的圆上六点,则六边形ABCDEF即为所求作的正六边形.
例
利用尺规作图,作出已知圆的内接正方形和内接正六边形.
试一试
你还有别的方法来作出已知圆的内接正六边形吗?
作法:(1)作⊙O
的任意直径
BE,分别以
B,E
为圆心,以圆的半径长为半径作圆,与⊙O分别相交于点
A,C
和
F,D.
(2)
依次连结
AB,BC,CD,DE,EF,
FA,则六边形
ABCDEF
就是所求作的⊙O
的内接正六边形.
练习
1.使用量角器画出圆的内接正九边形
2.使用尺规作图,作出圆的内接正十二边形
自己动手画一画
1.下列命题不正确的有
(填所有正确答案的序号).
①将一个圆分成4份,依次连结各分点所得的四边形是正方形
②正三角形外接圆的圆心叫作正三角形的中心
③正方形外接圆的半径等于其边长
④正五边形的中心角等于72°
基础巩固
随堂演练
①③
2.若正方形的边长为6,则其外接圆半径与内切圆半径的大小分别为(
)
A.
6
,
3
B.3
,
3
C.6
,
3
D.6
,
3
B
3.如图,
正六边形
ABCDEF
内接于☉O,
☉O
的半径为
6,
OM
⊥
BC
于点
M
,
则
OM
的长为
_______.
课堂小结
1.任何正多边形都有一个外接圆和一个内切圆.
2.这两个圆有公共的圆心,称其为正多边形的中心.外接圆的半径叫作正多边形的半径,内切圆的半径叫作正多边形的边心距.
3.正多边形每一条边所对的外接圆的圆心角都相等,叫作正多边形的中心角.
课堂小结
正多边形与圆的关系:
把圆分成n(n>2)等份,依次连结各分点所得的多边形是这个圆的一个内接正n边形.
课堂小结
尺规作图
量角器作图
作内接多边形的方法
1.从课后习题中选取;
2.完成练习册本课时的习题.
课后作业
27.4
正多边形和圆
华东师大·九年级下册
新课导入
观察下面图形,你能说出这些图形的特征吗?
三边相等,三个角也相等
(60°)
四边相等,四个角也相等
(90°)
五边相等,五个角也相等
(108°)
正多边形
新课导入
想一想:
各边相等的多边形一定是正多边形吗?各角相等的多边形呢?请举例说明.
各边相等的多边形不一定是正多边形,例如菱形.
各角相等的多边形不一定是正多边形,例如长方形.
我们已经知道,各条边相等、各个角也相等的多边形是
正多边形.等边三角形是正三角形,正方形是正四边形.正
多边形都是轴对称图形,在日常生活和美术设计中都很常见.
推进新课
外接圆和内切圆
知识点1
分别画出图中各正多边形的对称轴.看看能发现什么结果?
思考:正n边形共有多少条对称轴?
推进新课
A
B
C
D
E
F
G
H
I
J
O
以正五边形为例,我们发现正五边形有
对称轴,而且这些对称轴
.
根据对称轴的性质,我们知道这些对称轴是正五边形各边的
,因而点O到正五边形各个顶点的
,记为R.
以点O为圆心、R为半径的圆过正五边形的各个顶点,它是该正五边形的
.
五条
交于一点O
垂直平分线
距离相等
外接圆
推进新课
A
B
C
D
E
F
G
H
I
J
O
这些对称轴也是各内角的
.
根据角平分线的性质,点O到各边的距离都
,记为r.
相等
以点O为圆心、r为半径的圆与正五边形的各条边相切,它是该正五边形的
.
内切圆
平分线
思考
试一试其他的正多边形是否也有类似的结论
任何正多边形都有一个外接圆和一个内切圆
.
.
O
中心角
半径R
边心距r
正多边形的中心:一个正多边形的外接圆或内切圆的圆心.
正多边形的半径:外接圆的半径
正多边形的中心角:正多边形的每一条边所对的圆心角.
正多边形的边心距:中心到正多边形的一边的距离.
A
B
C
D
E
F
O
中心角
边心距把△BOC分成2个
的直角三角形.
A
B
C
D
E
F
全等
.
练习
如果正n边形的中心角等于24°,求这个正多边形的边数.
解:由题意得:
24×n=360
n=15
这个正多边形的边数为15.
如图,在⊙O中,
,那么弦AB、BC、CD、DE、EA之间有什么关系?∠A、∠B、∠C、∠D、∠E之间又有什么关系?
在同一个圆中,等弧对等弦,
因此AB=BC=CD=DE=EA,
而根据圆周角定理,有∠A=∠B=∠C=∠D=∠E,
因此五边形ABCDE是正五边形.
正多边形的画法
知识点2
这样我们就得到下面正多边形与圆的关系:
把圆分成n(n>2)等份,依次连结各分点所得的多边形是这个圆的一个内接正n边形.
例
利用尺规作图,作出已知圆的内接正方形和内接正六边形.
解:内接正方形的做法:
(1)用直尺任作圆的一条直径AC;
(2)作与直径AC垂直的直径BD;
(3)顺次连结所得的圆上四点,则四边形ABCD即为所求作的正方形.
内接正六边形的作法:
(1)用直尺任作圆的一条直径AD;
(2)以点A为圆心、OA为半径作圆,与⊙O交于点B、F;
(3)以点D为圆心、OD为半径作圆,与⊙O交于点C、E;
(4)顺次连结所得的圆上六点,则六边形ABCDEF即为所求作的正六边形.
例
利用尺规作图,作出已知圆的内接正方形和内接正六边形.
内接正六边形的做法:
(1)任意作圆的一条半径OA;
(2)沿半径OA用量角器量出正六边形中心角的度数(60°),与⊙O交于点B;
(3)依次量出C、D、E、F
;
(4)顺次连结所得的圆上六点,则六边形ABCDEF即为所求作的正六边形.
例
利用尺规作图,作出已知圆的内接正方形和内接正六边形.
试一试
你还有别的方法来作出已知圆的内接正六边形吗?
作法:(1)作⊙O
的任意直径
BE,分别以
B,E
为圆心,以圆的半径长为半径作圆,与⊙O分别相交于点
A,C
和
F,D.
(2)
依次连结
AB,BC,CD,DE,EF,
FA,则六边形
ABCDEF
就是所求作的⊙O
的内接正六边形.
练习
1.使用量角器画出圆的内接正九边形
2.使用尺规作图,作出圆的内接正十二边形
自己动手画一画
1.下列命题不正确的有
(填所有正确答案的序号).
①将一个圆分成4份,依次连结各分点所得的四边形是正方形
②正三角形外接圆的圆心叫作正三角形的中心
③正方形外接圆的半径等于其边长
④正五边形的中心角等于72°
基础巩固
随堂演练
①③
2.若正方形的边长为6,则其外接圆半径与内切圆半径的大小分别为(
)
A.
6
,
3
B.3
,
3
C.6
,
3
D.6
,
3
B
3.如图,
正六边形
ABCDEF
内接于☉O,
☉O
的半径为
6,
OM
⊥
BC
于点
M
,
则
OM
的长为
_______.
课堂小结
1.任何正多边形都有一个外接圆和一个内切圆.
2.这两个圆有公共的圆心,称其为正多边形的中心.外接圆的半径叫作正多边形的半径,内切圆的半径叫作正多边形的边心距.
3.正多边形每一条边所对的外接圆的圆心角都相等,叫作正多边形的中心角.
课堂小结
正多边形与圆的关系:
把圆分成n(n>2)等份,依次连结各分点所得的多边形是这个圆的一个内接正n边形.
课堂小结
尺规作图
量角器作图
作内接多边形的方法
1.从课后习题中选取;
2.完成练习册本课时的习题.
课后作业
