2021-2022学年华东师大版数学九年级下册第27章 圆 复习课件(44张PPT)
文档属性
| 名称 | 2021-2022学年华东师大版数学九年级下册第27章 圆 复习课件(44张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-06 12:27:38 | ||
图片预览



文档简介
(共44张PPT)
华东师大版·九年级下册
章末复习
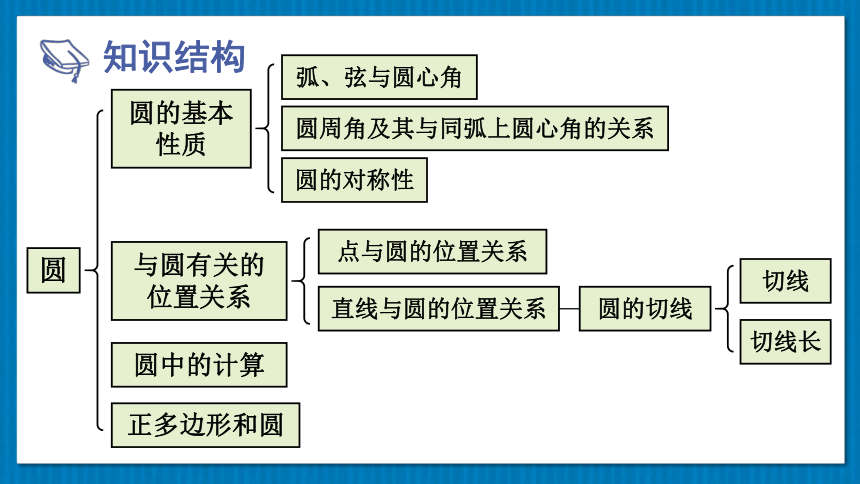
知识结构
圆
圆的基本性质
与圆有关的位置关系
圆中的计算
正多边形和圆
弧、弦与圆心角
圆周角及其与同弧上圆心角的关系
圆的对称性
点与圆的位置关系
直线与圆的位置关系
圆的切线
切线长
切线
知识梳理
1.圆的定义:
平面内到定点的距离等于定长的所有点组成的图形.
2.与圆相关的概念:
①弦和直径;
②弧、半圆、优弧、劣弧;
③等圆;
④等弧;
⑤圆心角.
.
O
n
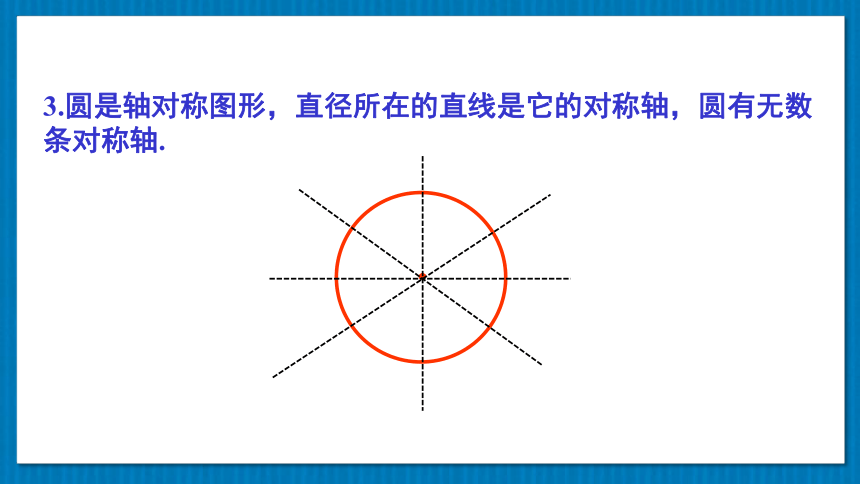
3.圆是轴对称图形,直径所在的直线是它的对称轴,圆有无数条对称轴.
.
4.垂径定理及垂径定理推论.
垂径定理:垂直于弦的直径平分这条弦,并且平分弦所对的两条弧.
∵CD是圆O的直径,CD⊥AB
∴AP=BP,
AC=BC
AD=BD
.
A
D
B
P
C
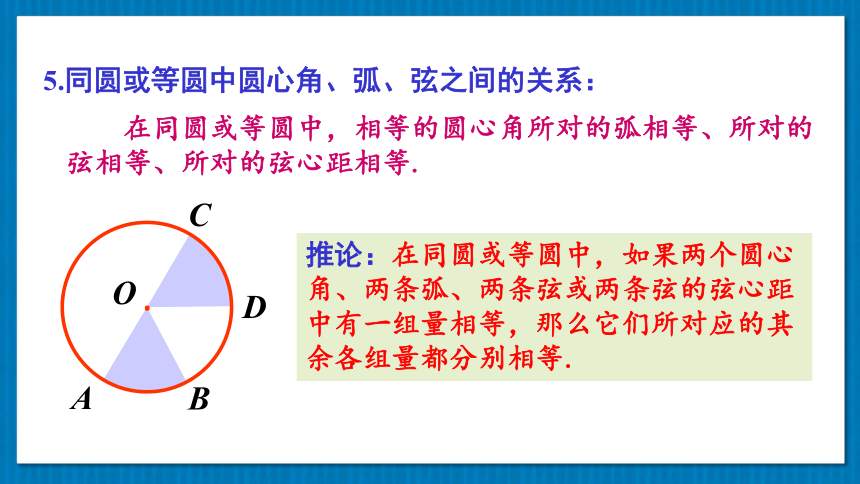
5.同圆或等圆中圆心角、弧、弦之间的关系:
.
A
O
B
C
D
推论:在同圆或等圆中,如果两个圆心角、两条弧、两条弦或两条弦的弦心距中有一组量相等,那么它们所对应的其余各组量都分别相等.
在同圆或等圆中,相等的圆心角所对的弧相等、所对的弦相等、所对的弦心距相等.
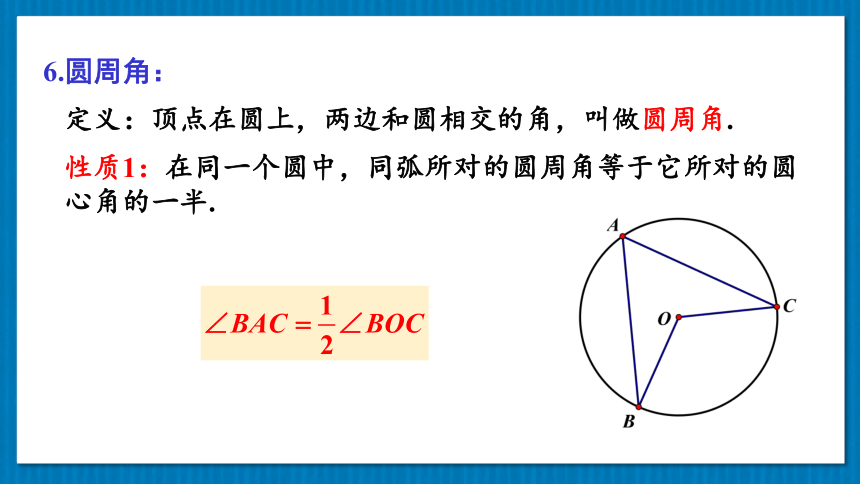
6.圆周角:
定义:顶点在圆上,两边和圆相交的角,叫做圆周角.
性质1:在同一个圆中,同弧所对的圆周角等于它所对的圆心角的一半.
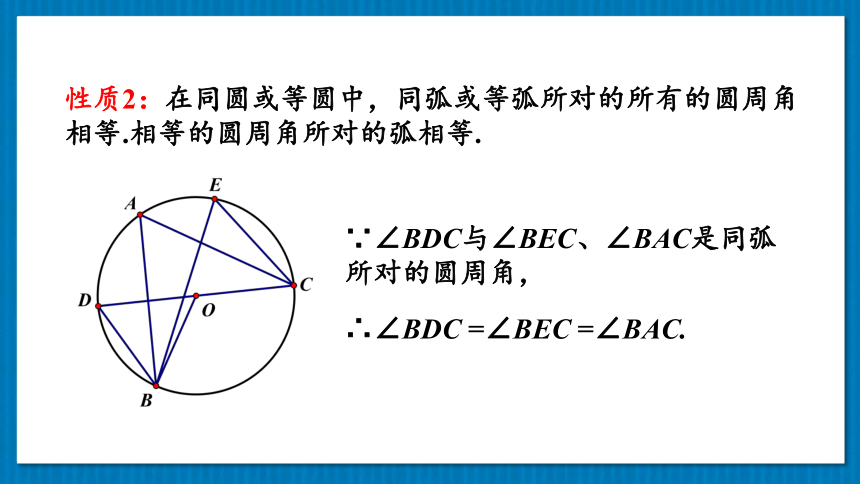
性质2:在同圆或等圆中,同弧或等弧所对的所有的圆周角相等.相等的圆周角所对的弧相等.
∵∠BDC与∠BEC、∠BAC是同弧所对的圆周角,
∴∠BDC
=∠BEC
=∠BAC.
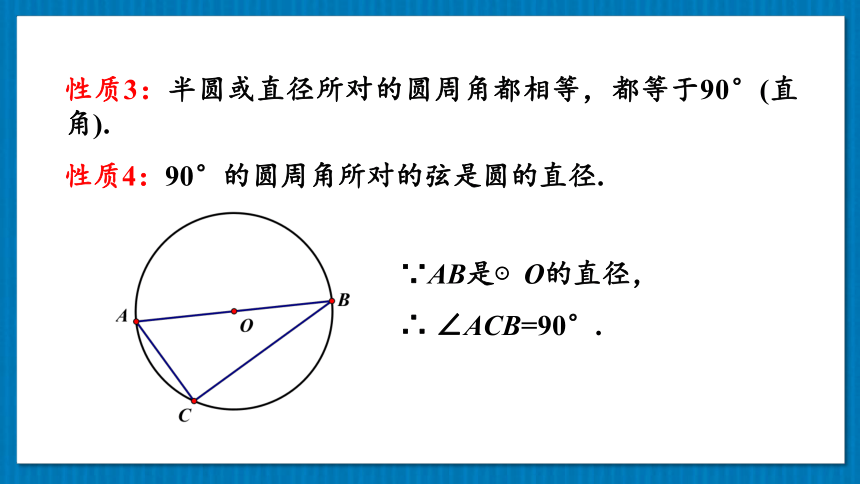
性质3:半圆或直径所对的圆周角都相等,都等于90°(直角).
性质4:90°的圆周角所对的弦是圆的直径.
∵AB是⊙O的直径,
∴
∠ACB=90°.
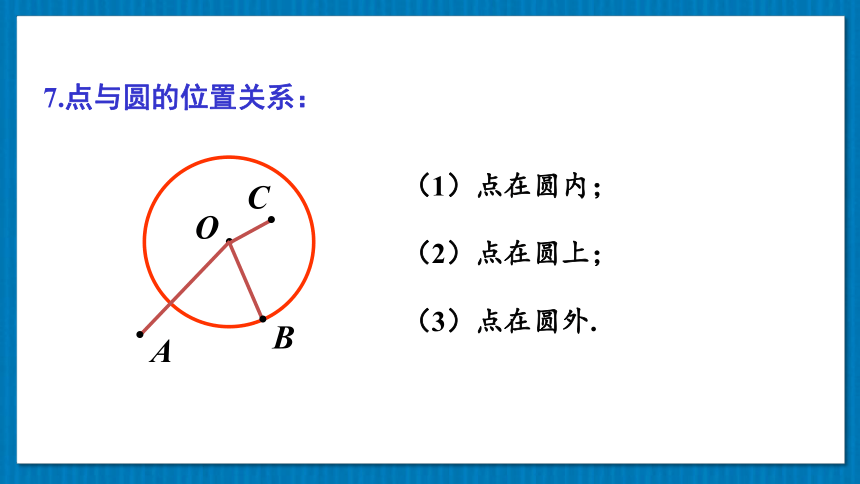
7.点与圆的位置关系:
.
A
O
B
C
.
.
.
(2)点在圆上;
(3)点在圆外.
(1)点在圆内;
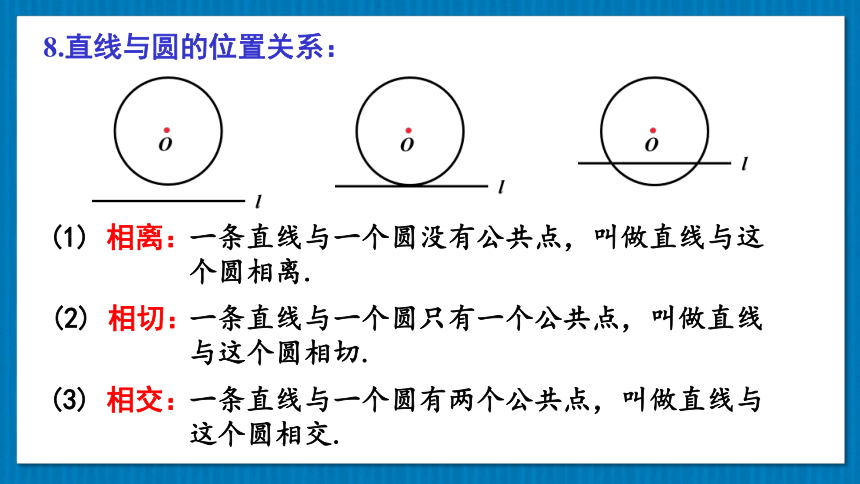
8.直线与圆的位置关系:
(1)
相离:
一条直线与一个圆没有公共点,叫做直线与这个圆相离.
(2)
相切:
一条直线与一个圆只有一个公共点,叫做直线与这个圆相切.
(3)
相交:
一条直线与一个圆有两个公共点,叫做直线与这个圆相交.
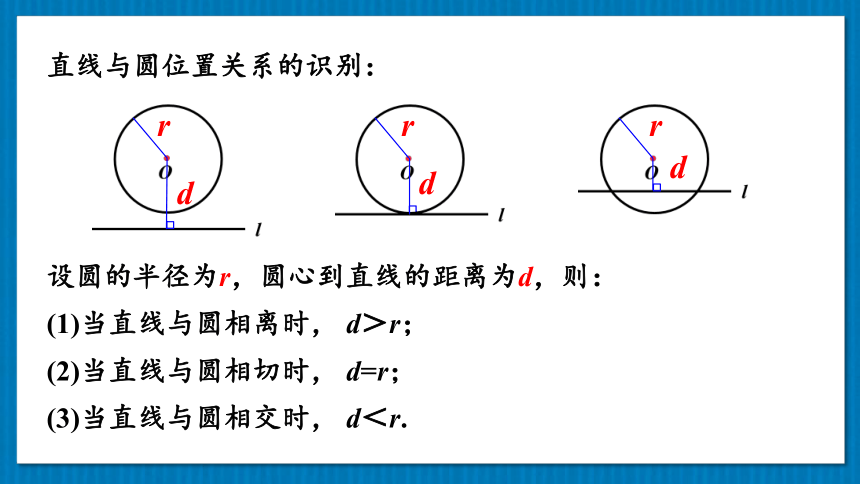
直线与圆位置关系的识别:
r
d
r
d
r
d
设圆的半径为r,圆心到直线的距离为d,则:
(1)当直线与圆相离时,
d>r;
(2)当直线与圆相切时,
d=r;
(3)当直线与圆相交时,
d<r.
9.切线的性质定理及推论:
切线的识别方法:
a.与圆有一个公共点的直线.
b.圆心到直线的距离等于圆的半径的直线是圆的切线.
c.经过半径的外端且垂直于这条半径的直线是圆的切线.
A
∵OA是半径,OA⊥
l
∴直线l是⊙O的切线.
切线的性质:
(1)圆的切线垂直于经过切点的半径;
(2)经过圆心垂直于切线的直线必经过切点;
(3)经过切点垂直于切线的直线必经过圆心.
A
∴
OA⊥
l
.
∵直线l是⊙O的切线,切点为A,
切线长定理:
过圆外一点所画的圆的两条切线,它们的切线长相等.这一点和圆心的连线平分这两条切线的夹角.
几何语言:
PA、PB分别切⊙O于A、B
PA
=
PB
∠APO=∠BPO
与三角形三边都相切的圆叫做三角形的内切圆,内切圆的圆心叫做三角形的内心,这个三角形叫做圆的外切三角形.
三角形的内心到三角形的三边距离相等.
10.弧长及扇形的面积:
n°
11.圆锥的相关计算:
A
O
r
h
l
R
B
O
C
a
n
12.正多边形与圆的关系:
(1)有关概念
(2)常用的方法
(3)正多边形的作图
13.正多边形与圆的关系:
E
F
C
D
.
O
中心角
半径R
边心距r
正多边形的中心:该正多边形的外接圆的圆心.
正多边形的半径:外接圆的半径.
正多边形的中心角:正多边形的每一条边所对的圆心角.
正多边形的边心距:中心到正多边形的一边的距离.
A
B
复习题
A组
1.生活中有许多由圆组成的图案,请你用圆规等作图工具设计一个美丽的图案.
图案有多种,同学们可自己动手设计.
2.如图,试列举出⊙A中的一条直径、两条半径、三条弦、三段弧、三个圆周角和三个圆心角.
解:直径:CD;
半径:AB、AE;
弦:CE、BF、ED;
弧:
;
圆周角:∠ECD、∠CBF、∠D;
圆心角:∠EAD、∠BAC、∠CAF.
3.如图,在⊙O中,AB是⊙O的直径,∠AOC=130°,则∠D
=_______°.
25
4.如图,AB是⊙O的直径,BC、CD、DA是⊙O的弦,且BC=CD=DA,则∠BOD=_______°.
120
5.如图,AB是⊙O的直径,弦CD⊥AB,BC=1cm,AD=4cm,那么BD=_____cm,AC=_____cm,⊙O的周长为_____cm.
1
4
10
6.⊙O的半径为r,某直线与该圆有公共点,且与圆心的距离为d,则(
).
A.
d
=
r
B.
d
<
r
C
.
d
>
r
D.
d
≤
r
D
7.小张要给一个圆锥模型贴上保护膜.他用半径为20cm、圆心角为108°的扇形薄膜片恰好贴满了这个圆锥的侧面,那么他还要用半径为多少厘米的圆形薄膜片才能刚好贴满圆锥的底面?
解:设该圆锥的底面半径为r
cm.
根据题意,得
.
解得r=6.
即该圆锥的底面半径为6cm.
8.如图,AB是⊙O的直径,⊙O的半径为6.5cm,弦AC的长为5cm.求弦BC的长.
解:∵AB为直径,∴∠C=90°.
∵圆的半径为6.5cm,∴AB=2×6.5=13(cm),
∵AC=5cm,
由勾股定理,得BC=
9.如图,∠ACB=∠CDB=60°,AC=2cm.求△ABC的周长.
解:∵∠ACB=∠CDB=60°,∠CDB=∠A,
∴∠A=∠ACB=60°,
∴△ABC为等边三角形,
∴△ABC的周长为3×2=6(cm).
10.直线PA、PB是⊙O的两条切线,A、B分别为切点,且∠APB=120°,⊙O的半径为4cm.求切线长PA.(结果保留根号)
解:如图.连结OA、OB、OP.
由切线长定理,得∠APO=∠BPO.
∵∠APB=120°,
∴∠APO=60°.
又∵∠OAP=90°,OA=4,
∴∠AOP=30°,
∴PA=OA·tan30°=
(cm).
11.有一个边长为6cm的正六边形,若要剪一张圆形纸片完全盖住这个图形,求这个圆形纸片的最小半径.
解:由题意得这个圆形纸片即为正六边形的外接圆,最小半径为6cm.
B组
12.如图,⊙I是△ABC的内切圆,与AB、BC、CA分别相切于点D、E、F,∠DEF=50°.求∠A的大小.
解:连结ID、IF,则ID⊥AB,IF⊥AC.
∵∠DEF=50°,
∴∠DIF=2
,
∠DEF=100°,
∴∠A=360°-90°-90°-100°=80°.
13.如图,在△ABC中,AD、BD分别平分∠BAC和∠ABC,延长AD交△ABC的外接圆于点E,连接BE.求证:BE=DE.
证明:∵AD、BD分别平分∠BAC、∠ABC,∴∠BAE=∠EAC,∠ABD=∠DBC.
∵∠EBC=∠EAC,
则∠EBD=∠EBC+∠CBD=∠EAC+∠CBD=
∠EAB+∠ABD=∠BDE,
∴BE=DE.
14.如图,⊙O是△ABC的外接圆,∠ACO=30°.求∠B的大小.
解:连接AO.
∵OA=OC,∠ACO=30°,
∴∠CAO=∠ACO=30°,
∴∠B=
∠AOC
=
×(180°-30°-30°)=60°.
15.如图,⊙I为△ABC的内切圆,AB=9,BC=8,CA=10,点D、E分别为AB、AC上的点,且DE为⊙I的切线.求△ADE的周长.
H
F
P
解:过点I作IH⊥BC于点H,IP⊥AC于点P,IF⊥AB于点F.
∵⊙I是△ABC的内切圆,
∴点H、P、F分别为⊙I与BC、AC、AB边的切点.
设AF=AP=x,BF=BH=y,CP=CH=z.
H
F
P
G
由AB=9,BC=8,CA=10,得
设DE与⊙I的切点为G,则DG=DF,EG=EP.
∴△ADE的周长=AD+AE+DE=AD+AE+DG+EG=AD+DF+AE+
EP=AF+AP=2x=11.
即△ADE的周长为11.
16.如图,⊙O的内接正五边形ABCDE的对角线AD与BE相交于点M.
(1)写出图中所有的等腰三角形(不添加其他线段);
(2)求证:BM2=BE·ME.
(1)解:△ABE、△AED、△AME.
(2)证明:正五边形的外角度数为360°÷5=72°.
AB=AE,EA=ED.
∴∠ABE=∠AEB=∠EAD=∠EDA=72°÷2=36°.
∴△MAE和△ABE都是底角为36°的等腰三角形,
∴△MAE~△ABE,
∴
,∴AE2=ME·BE.
∵∠AMB=∠AEM+∠MAE=72°,
∠BAM=180°-∠AMB-∠ABM=72°,
∴∠AMB=∠BAM,∴BA=BM=AE.
∴BM2=ME·BE.
C组
17.如图,已知⊙O1与⊙O2相交于点A、B,过点B作CD⊥AB,分别交⊙O1和⊙O2于点C、D,过点B任作一条直线分别交⊙O1和⊙O2于点E、F.求证:
(1)AC、AD分别是⊙O1和⊙O2的直径;
(2)AE与AF的比值是一个常数.
(1)证明:∵CD⊥AB,
∴∠ABC=∠ABD=90°,
∴AC、AD分别为⊙O1、⊙O2的直径.
(2)证明:如图,连接EC、FD.
∵AC、AD分别为⊙O1、⊙O2的直径,∴∠AEC=∠AFD=90°.
又∵∠CAE=∠CBE,∠DAF=∠DBF,∠CBE=∠DBF.
∴∠CAE=∠DAF,∴△ACE~△ADF,
∴
∵两个圆的半径为定值,
∴AE与AF的比值是一个常数.
18.如图,AB是半圆的直径,AC是一条弦,D是AC的中点,DE⊥AB于点E,交AC于点F,DB交AC于点G.求证:AF=FG.
证明:如图,连接AD.
∵AB为半圆的直径,∴∠ADB=90°.
在Rt△ADE中,∠ADE=90°-∠DAE,
在Rt△ADB中,∠ABD=90°-∠DAE,
∴∠ADE=∠ABD.
又∵点D是AC的中点,∴∠DAC=∠ABD,
∴∠DAF=∠ADF,∴DF=AF.
又∵△ADG为直角三角形,∴AF=DF=FG.
19.
(1)根据图中数据,分别求出图中∠x的大小.
解:(题中左图)∵∠C=∠A=20°,∠x+∠C=∠ABC=50°,
∴∠x=50°-∠C=30°;
(题中右图)∵∠D=∠A=70°,∠D+∠C=∠x,∠C=30°,
∴∠x=∠D+∠C=70°+30°=100°.
(2)根据题(1)的计算过程与结果,猜想下图中所标的两角大小的计算方法,并说明理由.
解:若点P在圆外,则∠P=α-β,其中α和β分别表示∠P的两边与圆相交时所夹的两段弧的度数,且α>β;若点P在圆内,则∠P=α+β其中α和β分别表示∠P的两边及其顶角与圆所夹的两段弧的度数.
课后作业
1.从课后习题中选取;
2.完成练习册本课时的习题.
华东师大版·九年级下册
章末复习
知识结构
圆
圆的基本性质
与圆有关的位置关系
圆中的计算
正多边形和圆
弧、弦与圆心角
圆周角及其与同弧上圆心角的关系
圆的对称性
点与圆的位置关系
直线与圆的位置关系
圆的切线
切线长
切线
知识梳理
1.圆的定义:
平面内到定点的距离等于定长的所有点组成的图形.
2.与圆相关的概念:
①弦和直径;
②弧、半圆、优弧、劣弧;
③等圆;
④等弧;
⑤圆心角.
.
O
n
3.圆是轴对称图形,直径所在的直线是它的对称轴,圆有无数条对称轴.
.
4.垂径定理及垂径定理推论.
垂径定理:垂直于弦的直径平分这条弦,并且平分弦所对的两条弧.
∵CD是圆O的直径,CD⊥AB
∴AP=BP,
AC=BC
AD=BD
.
A
D
B
P
C
5.同圆或等圆中圆心角、弧、弦之间的关系:
.
A
O
B
C
D
推论:在同圆或等圆中,如果两个圆心角、两条弧、两条弦或两条弦的弦心距中有一组量相等,那么它们所对应的其余各组量都分别相等.
在同圆或等圆中,相等的圆心角所对的弧相等、所对的弦相等、所对的弦心距相等.
6.圆周角:
定义:顶点在圆上,两边和圆相交的角,叫做圆周角.
性质1:在同一个圆中,同弧所对的圆周角等于它所对的圆心角的一半.
性质2:在同圆或等圆中,同弧或等弧所对的所有的圆周角相等.相等的圆周角所对的弧相等.
∵∠BDC与∠BEC、∠BAC是同弧所对的圆周角,
∴∠BDC
=∠BEC
=∠BAC.
性质3:半圆或直径所对的圆周角都相等,都等于90°(直角).
性质4:90°的圆周角所对的弦是圆的直径.
∵AB是⊙O的直径,
∴
∠ACB=90°.
7.点与圆的位置关系:
.
A
O
B
C
.
.
.
(2)点在圆上;
(3)点在圆外.
(1)点在圆内;
8.直线与圆的位置关系:
(1)
相离:
一条直线与一个圆没有公共点,叫做直线与这个圆相离.
(2)
相切:
一条直线与一个圆只有一个公共点,叫做直线与这个圆相切.
(3)
相交:
一条直线与一个圆有两个公共点,叫做直线与这个圆相交.
直线与圆位置关系的识别:
r
d
r
d
r
d
设圆的半径为r,圆心到直线的距离为d,则:
(1)当直线与圆相离时,
d>r;
(2)当直线与圆相切时,
d=r;
(3)当直线与圆相交时,
d<r.
9.切线的性质定理及推论:
切线的识别方法:
a.与圆有一个公共点的直线.
b.圆心到直线的距离等于圆的半径的直线是圆的切线.
c.经过半径的外端且垂直于这条半径的直线是圆的切线.
A
∵OA是半径,OA⊥
l
∴直线l是⊙O的切线.
切线的性质:
(1)圆的切线垂直于经过切点的半径;
(2)经过圆心垂直于切线的直线必经过切点;
(3)经过切点垂直于切线的直线必经过圆心.
A
∴
OA⊥
l
.
∵直线l是⊙O的切线,切点为A,
切线长定理:
过圆外一点所画的圆的两条切线,它们的切线长相等.这一点和圆心的连线平分这两条切线的夹角.
几何语言:
PA、PB分别切⊙O于A、B
PA
=
PB
∠APO=∠BPO
与三角形三边都相切的圆叫做三角形的内切圆,内切圆的圆心叫做三角形的内心,这个三角形叫做圆的外切三角形.
三角形的内心到三角形的三边距离相等.
10.弧长及扇形的面积:
n°
11.圆锥的相关计算:
A
O
r
h
l
R
B
O
C
a
n
12.正多边形与圆的关系:
(1)有关概念
(2)常用的方法
(3)正多边形的作图
13.正多边形与圆的关系:
E
F
C
D
.
O
中心角
半径R
边心距r
正多边形的中心:该正多边形的外接圆的圆心.
正多边形的半径:外接圆的半径.
正多边形的中心角:正多边形的每一条边所对的圆心角.
正多边形的边心距:中心到正多边形的一边的距离.
A
B
复习题
A组
1.生活中有许多由圆组成的图案,请你用圆规等作图工具设计一个美丽的图案.
图案有多种,同学们可自己动手设计.
2.如图,试列举出⊙A中的一条直径、两条半径、三条弦、三段弧、三个圆周角和三个圆心角.
解:直径:CD;
半径:AB、AE;
弦:CE、BF、ED;
弧:
;
圆周角:∠ECD、∠CBF、∠D;
圆心角:∠EAD、∠BAC、∠CAF.
3.如图,在⊙O中,AB是⊙O的直径,∠AOC=130°,则∠D
=_______°.
25
4.如图,AB是⊙O的直径,BC、CD、DA是⊙O的弦,且BC=CD=DA,则∠BOD=_______°.
120
5.如图,AB是⊙O的直径,弦CD⊥AB,BC=1cm,AD=4cm,那么BD=_____cm,AC=_____cm,⊙O的周长为_____cm.
1
4
10
6.⊙O的半径为r,某直线与该圆有公共点,且与圆心的距离为d,则(
).
A.
d
=
r
B.
d
<
r
C
.
d
>
r
D.
d
≤
r
D
7.小张要给一个圆锥模型贴上保护膜.他用半径为20cm、圆心角为108°的扇形薄膜片恰好贴满了这个圆锥的侧面,那么他还要用半径为多少厘米的圆形薄膜片才能刚好贴满圆锥的底面?
解:设该圆锥的底面半径为r
cm.
根据题意,得
.
解得r=6.
即该圆锥的底面半径为6cm.
8.如图,AB是⊙O的直径,⊙O的半径为6.5cm,弦AC的长为5cm.求弦BC的长.
解:∵AB为直径,∴∠C=90°.
∵圆的半径为6.5cm,∴AB=2×6.5=13(cm),
∵AC=5cm,
由勾股定理,得BC=
9.如图,∠ACB=∠CDB=60°,AC=2cm.求△ABC的周长.
解:∵∠ACB=∠CDB=60°,∠CDB=∠A,
∴∠A=∠ACB=60°,
∴△ABC为等边三角形,
∴△ABC的周长为3×2=6(cm).
10.直线PA、PB是⊙O的两条切线,A、B分别为切点,且∠APB=120°,⊙O的半径为4cm.求切线长PA.(结果保留根号)
解:如图.连结OA、OB、OP.
由切线长定理,得∠APO=∠BPO.
∵∠APB=120°,
∴∠APO=60°.
又∵∠OAP=90°,OA=4,
∴∠AOP=30°,
∴PA=OA·tan30°=
(cm).
11.有一个边长为6cm的正六边形,若要剪一张圆形纸片完全盖住这个图形,求这个圆形纸片的最小半径.
解:由题意得这个圆形纸片即为正六边形的外接圆,最小半径为6cm.
B组
12.如图,⊙I是△ABC的内切圆,与AB、BC、CA分别相切于点D、E、F,∠DEF=50°.求∠A的大小.
解:连结ID、IF,则ID⊥AB,IF⊥AC.
∵∠DEF=50°,
∴∠DIF=2
,
∠DEF=100°,
∴∠A=360°-90°-90°-100°=80°.
13.如图,在△ABC中,AD、BD分别平分∠BAC和∠ABC,延长AD交△ABC的外接圆于点E,连接BE.求证:BE=DE.
证明:∵AD、BD分别平分∠BAC、∠ABC,∴∠BAE=∠EAC,∠ABD=∠DBC.
∵∠EBC=∠EAC,
则∠EBD=∠EBC+∠CBD=∠EAC+∠CBD=
∠EAB+∠ABD=∠BDE,
∴BE=DE.
14.如图,⊙O是△ABC的外接圆,∠ACO=30°.求∠B的大小.
解:连接AO.
∵OA=OC,∠ACO=30°,
∴∠CAO=∠ACO=30°,
∴∠B=
∠AOC
=
×(180°-30°-30°)=60°.
15.如图,⊙I为△ABC的内切圆,AB=9,BC=8,CA=10,点D、E分别为AB、AC上的点,且DE为⊙I的切线.求△ADE的周长.
H
F
P
解:过点I作IH⊥BC于点H,IP⊥AC于点P,IF⊥AB于点F.
∵⊙I是△ABC的内切圆,
∴点H、P、F分别为⊙I与BC、AC、AB边的切点.
设AF=AP=x,BF=BH=y,CP=CH=z.
H
F
P
G
由AB=9,BC=8,CA=10,得
设DE与⊙I的切点为G,则DG=DF,EG=EP.
∴△ADE的周长=AD+AE+DE=AD+AE+DG+EG=AD+DF+AE+
EP=AF+AP=2x=11.
即△ADE的周长为11.
16.如图,⊙O的内接正五边形ABCDE的对角线AD与BE相交于点M.
(1)写出图中所有的等腰三角形(不添加其他线段);
(2)求证:BM2=BE·ME.
(1)解:△ABE、△AED、△AME.
(2)证明:正五边形的外角度数为360°÷5=72°.
AB=AE,EA=ED.
∴∠ABE=∠AEB=∠EAD=∠EDA=72°÷2=36°.
∴△MAE和△ABE都是底角为36°的等腰三角形,
∴△MAE~△ABE,
∴
,∴AE2=ME·BE.
∵∠AMB=∠AEM+∠MAE=72°,
∠BAM=180°-∠AMB-∠ABM=72°,
∴∠AMB=∠BAM,∴BA=BM=AE.
∴BM2=ME·BE.
C组
17.如图,已知⊙O1与⊙O2相交于点A、B,过点B作CD⊥AB,分别交⊙O1和⊙O2于点C、D,过点B任作一条直线分别交⊙O1和⊙O2于点E、F.求证:
(1)AC、AD分别是⊙O1和⊙O2的直径;
(2)AE与AF的比值是一个常数.
(1)证明:∵CD⊥AB,
∴∠ABC=∠ABD=90°,
∴AC、AD分别为⊙O1、⊙O2的直径.
(2)证明:如图,连接EC、FD.
∵AC、AD分别为⊙O1、⊙O2的直径,∴∠AEC=∠AFD=90°.
又∵∠CAE=∠CBE,∠DAF=∠DBF,∠CBE=∠DBF.
∴∠CAE=∠DAF,∴△ACE~△ADF,
∴
∵两个圆的半径为定值,
∴AE与AF的比值是一个常数.
18.如图,AB是半圆的直径,AC是一条弦,D是AC的中点,DE⊥AB于点E,交AC于点F,DB交AC于点G.求证:AF=FG.
证明:如图,连接AD.
∵AB为半圆的直径,∴∠ADB=90°.
在Rt△ADE中,∠ADE=90°-∠DAE,
在Rt△ADB中,∠ABD=90°-∠DAE,
∴∠ADE=∠ABD.
又∵点D是AC的中点,∴∠DAC=∠ABD,
∴∠DAF=∠ADF,∴DF=AF.
又∵△ADG为直角三角形,∴AF=DF=FG.
19.
(1)根据图中数据,分别求出图中∠x的大小.
解:(题中左图)∵∠C=∠A=20°,∠x+∠C=∠ABC=50°,
∴∠x=50°-∠C=30°;
(题中右图)∵∠D=∠A=70°,∠D+∠C=∠x,∠C=30°,
∴∠x=∠D+∠C=70°+30°=100°.
(2)根据题(1)的计算过程与结果,猜想下图中所标的两角大小的计算方法,并说明理由.
解:若点P在圆外,则∠P=α-β,其中α和β分别表示∠P的两边与圆相交时所夹的两段弧的度数,且α>β;若点P在圆内,则∠P=α+β其中α和β分别表示∠P的两边及其顶角与圆所夹的两段弧的度数.
课后作业
1.从课后习题中选取;
2.完成练习册本课时的习题.
