海南省海口市第一重点高中2021届高三上学期9月月考数学试题(Word版含简答)
文档属性
| 名称 | 海南省海口市第一重点高中2021届高三上学期9月月考数学试题(Word版含简答) |  | |
| 格式 | doc | ||
| 文件大小 | 826.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-06 09:55:33 | ||
图片预览




文档简介
海口一中2021届高三数学9月月考试题
一 单项选择题∶本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.
已知集合,,则(
)
A.
B.
C.
D.
2.
已知为虚数单位,复数满足,则共轭复数为(
)
A.
B.
C.
D.
3.
若,则(
)
A.
B.
C.
D.
4.
已知,且,则的最小值为(
)
A.
B.
C.
D.
5.
设,,,则(
)
A.
B.
C.
D.
6.
已知抛物线的焦点为,准线为,是上一点,直线与抛物线交于,两点,若,则=
A.
B.
C.
D.
7.
已知函数是定义在R上的奇函数,当时,,则使不等式成立的x的取值范围是(
)
A.
B.
C.
D.
8.
已知a1,a2,a3∈{2,4,6},记N(a1,a2,a3)为a1,a2,a3中不同数字的个数,如∶N(2,2,2)=1,N(2,4,2)=2,N(2,4,6)=3,则所有的(a1,a2,a3)的排列的N(a1,a2,a3)平均值为(
)
A.
B.
3
C.
D.
4
二 多项选择题∶本题共4小题,每小题5分,共20分,在每小题给出的选项中,有多项符合题目要求,全部选对的得5分,部分选对的得3分,有选错的得0分.
9.
已知为等差数列,其前项和为,且,则以下结论正确的是(
).
A.
B.
最小
C.
D.
10.
已知曲线的方程为,则下列结论正确的是(
)
A.
当时,曲线为椭圆,其焦距为
B.
当时,曲线为双曲线,其离心率为
C.
存在实数使得曲线为焦点在轴上双曲线
D.
当时,曲线为双曲线,其渐近线与圆相切
11.
设函数(),已知在有且仅有3个零点,下列结论正确的是(
)
A.
在上存在,,满足
B.
有且仅有1个最小值点
C.
在单调递增
D.
的取值范围是
12.
在三棱锥D-ABC中,,且,,M,N分别是棱BC,CD的中点,下面结论正确的是(
)
A.
B.
平面ABD
C.
三棱锥A-CMN的体积的最大值为
D.
AD与BC一定不垂直
三 填空题∶本题共4小题,每小题5分,共20分.
13.
左手掷一粒骰子,右手掷一枚硬币,则事件“骰子向上为6点且硬币向上为正面”的概率为_____.
14.
若展开式的二项式系数之和是,则__________;展开式中的常数项的值是__________.
15.
的内角、,的对边分别为、、,,已知向量,.若,则___________.
16.
设,分别是椭圆的左 右焦点,过的直线交椭圆于,两点,且,,则椭圆的离心率为_________
四 解答题∶本题共6小题,共70分.解答应写出文字说明 证明过程或演算步骤.
17.
在①,,成等差数列.②,,成等差数列中任选一个,补充在下列的问题中,并解答.
在公比为2的等比数列中,______
(1)求数列的通项公式;
(2)若,求数列的前n项和.
18.
设函数.
(1)若为函数的图像的一条对称轴,当时,求函数的最小值及相应的值;
(2)将函数的图象向左平移个单位得到函数的图像,已知,求的单调递减区间.
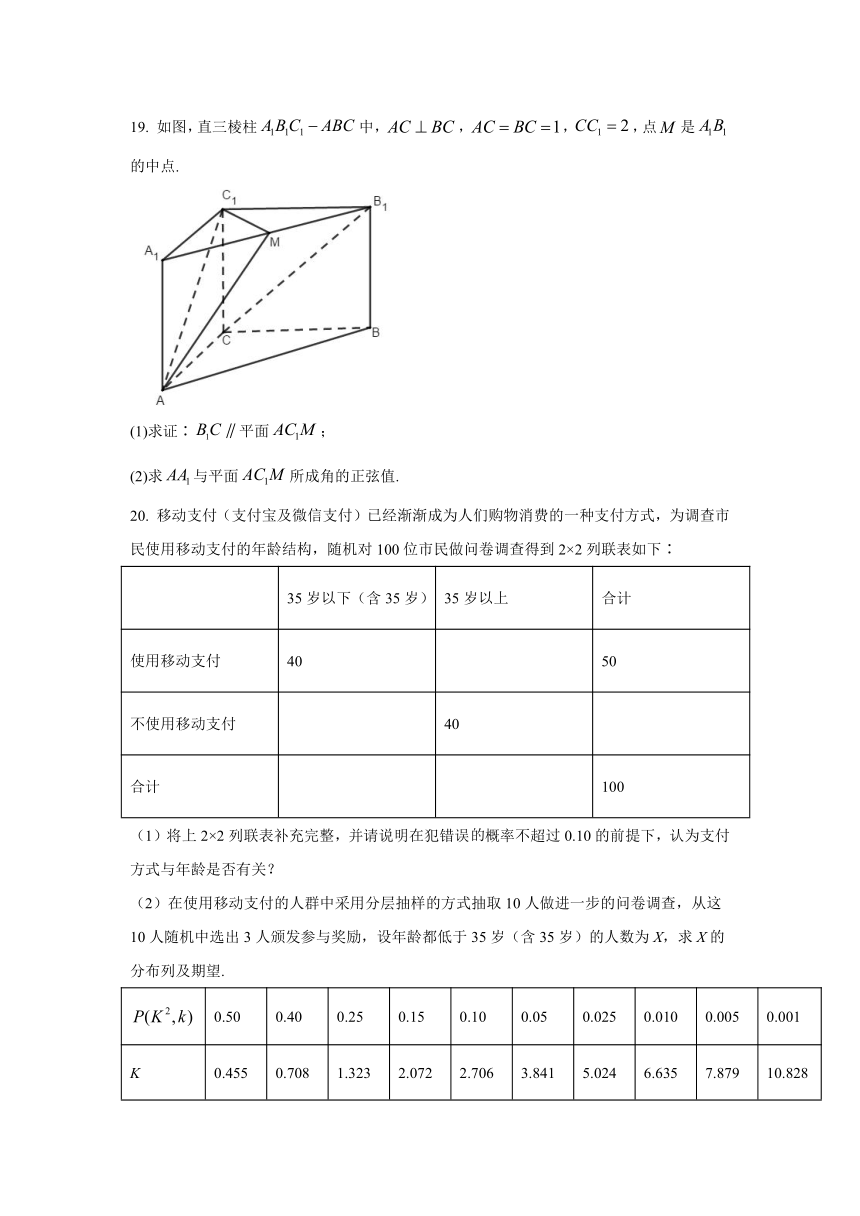
19.
如图,直三棱柱中,,,,点是的中点.
(1)求证∶平面;
(2)求与平面所成角的正弦值.
20.
移动支付(支付宝及微信支付)已经渐渐成为人们购物消费的一种支付方式,为调查市民使用移动支付的年龄结构,随机对100位市民做问卷调查得到2×2列联表如下∶
35岁以下(含35岁)
35岁以上
合计
使用移动支付
40
50
不使用移动支付
40
合计
100
(1)将上2×2列联表补充完整,并请说明在犯错误概率不超过0.10的前提下,认为支付方式与年龄是否有关?
(2)在使用移动支付的人群中采用分层抽样的方式抽取10人做进一步的问卷调查,从这10人随机中选出3人颁发参与奖励,设年龄都低于35岁(含35岁)的人数为X,求X的分布列及期望.
0.50
0.40
0.25
0.15
0.10
0.05
0.025
0.010
0.005
0.001
K
0.455
0.708
1.323
2.072
2.706
3.841
5.024
6.635
7.879
10.828
(参考公式:(其中n=a+b+c+d)
21.
已知椭圆的右焦点与抛物线焦点重合,且椭圆的离心率为,过轴正半轴一点且斜率为的直线交椭圆于两点.
(1)求椭圆的标准方程;
(2)是否存在实数使以线段为直径的圆经过点,若存在,求出实数的值;若不存在说明理由.
22.
已知函数 (为实常数).
(1)若,求曲线在处的切线方程;
(2)讨论函数在上的单调性;
(3)若存在,使得成立,求实数取值范围.
海口一中2021届高三数学9月月考试题
答案
一 单项选择题∶本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.
已知集合,,则(
)
A.
B.
C.
D.
答案:B
2.
已知为虚数单位,复数满足,则共轭复数为(
)
A.
B.
C.
D.
答案:C
3.
若,则(
)
A.
B.
C.
D.
答案:C
4.
已知,且,则的最小值为(
)
A.
B.
C.
D.
答案:C
5.
设,,,则(
)
A.
B.
C.
D.
答案:C
6.
已知抛物线的焦点为,准线为,是上一点,直线与抛物线交于,两点,若,则=
A.
B.
C.
D.
答案:B
7.
已知函数是定义在R上的奇函数,当时,,则使不等式成立的x的取值范围是(
)
A.
B.
C.
D.
答案:C
8.
已知a1,a2,a3∈{2,4,6},记N(a1,a2,a3)为a1,a2,a3中不同数字的个数,如∶N(2,2,2)=1,N(2,4,2)=2,N(2,4,6)=3,则所有的(a1,a2,a3)的排列的N(a1,a2,a3)平均值为(
)
A.
B.
3
C.
D.
4
答案:A
二 多项选择题∶本题共4小题,每小题5分,共20分,在每小题给出的选项中,有多项符合题目要求,全部选对的得5分,部分选对的得3分,有选错的得0分.
9.
已知为等差数列,其前项和为,且,则以下结论正确的是(
).
A.
B.
最小
C.
D.
答案:ACD
10.
已知曲线的方程为,则下列结论正确的是(
)
A.
当时,曲线为椭圆,其焦距为
B.
当时,曲线为双曲线,其离心率为
C.
存在实数使得曲线为焦点在轴上双曲线
D.
当时,曲线为双曲线,其渐近线与圆相切
答案:ABD
11.
设函数(),已知在有且仅有3个零点,下列结论正确的是(
)
A.
在上存在,,满足
B.
有且仅有1个最小值点
C.
在单调递增
D.
的取值范围是
答案:AB
12.
在三棱锥D-ABC中,,且,,M,N分别是棱BC,CD的中点,下面结论正确的是(
)
A.
B.
平面ABD
C.
三棱锥A-CMN的体积的最大值为
D.
AD与BC一定不垂直
答案:ABD
三 填空题∶本题共4小题,每小题5分,共20分.
13.
左手掷一粒骰子,右手掷一枚硬币,则事件“骰子向上为6点且硬币向上为正面”的概率为_____.
答案:
14.
若展开式的二项式系数之和是,则__________;展开式中的常数项的值是__________.
答案:
①.
②.
135
15.
的内角、,的对边分别为、、,,已知向量,.若,则___________.
答案:
16.
设,分别是椭圆的左 右焦点,过的直线交椭圆于,两点,且,,则椭圆的离心率为_________
答案:
四 解答题∶本题共6小题,共70分.解答应写出文字说明 证明过程或演算步骤.
17.
在①,,成等差数列.②,,成等差数列中任选一个,补充在下列的问题中,并解答.
在公比为2的等比数列中,______
(1)求数列的通项公式;
(2)若,求数列的前n项和.
答案:(1)(2)
18.
设函数.
(1)若为函数的图像的一条对称轴,当时,求函数的最小值及相应的值;
(2)将函数的图象向左平移个单位得到函数的图像,已知,求的单调递减区间.
答案:(1)当时,函数的最小值为;(2)单调递减区间为,.
19.
如图,直三棱柱中,,,,点是的中点.
(1)求证∶平面;
(2)求与平面所成角的正弦值.
答案:(1)证明见解析;(2).
20.
移动支付(支付宝及微信支付)已经渐渐成为人们购物消费的一种支付方式,为调查市民使用移动支付的年龄结构,随机对100位市民做问卷调查得到2×2列联表如下∶
35岁以下(含35岁)
35岁以上
合计
使用移动支付
40
50
不使用移动支付
40
合计
100
(1)将上2×2列联表补充完整,并请说明在犯错误概率不超过0.10的前提下,认为支付方式与年龄是否有关?
(2)在使用移动支付的人群中采用分层抽样的方式抽取10人做进一步的问卷调查,从这10人随机中选出3人颁发参与奖励,设年龄都低于35岁(含35岁)的人数为X,求X的分布列及期望.
0.50
0.40
0.25
0.15
0.10
0.05
0.025
0.010
0.005
0.001
K
0.455
0.708
1.323
2.072
2.706
3.841
5.024
6.635
7.879
10.828
(参考公式:(其中n=a+b+c+d)
答案:(1)列联表答案见解析,在犯错误的概率不超过0.10的前提下,认为支付方式与年龄有关;(2)分布列答案见解析,数学期望:.
21.
已知椭圆的右焦点与抛物线焦点重合,且椭圆的离心率为,过轴正半轴一点且斜率为的直线交椭圆于两点.
(1)求椭圆的标准方程;
(2)是否存在实数使以线段为直径的圆经过点,若存在,求出实数的值;若不存在说明理由.
答案:(1);(2)存在,.
22.
已知函数 (为实常数).
(1)若,求曲线在处的切线方程;
(2)讨论函数在上的单调性;
(3)若存在,使得成立,求实数取值范围.
答案:(1)y=1.(2)答案见解析;(3).
一 单项选择题∶本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.
已知集合,,则(
)
A.
B.
C.
D.
2.
已知为虚数单位,复数满足,则共轭复数为(
)
A.
B.
C.
D.
3.
若,则(
)
A.
B.
C.
D.
4.
已知,且,则的最小值为(
)
A.
B.
C.
D.
5.
设,,,则(
)
A.
B.
C.
D.
6.
已知抛物线的焦点为,准线为,是上一点,直线与抛物线交于,两点,若,则=
A.
B.
C.
D.
7.
已知函数是定义在R上的奇函数,当时,,则使不等式成立的x的取值范围是(
)
A.
B.
C.
D.
8.
已知a1,a2,a3∈{2,4,6},记N(a1,a2,a3)为a1,a2,a3中不同数字的个数,如∶N(2,2,2)=1,N(2,4,2)=2,N(2,4,6)=3,则所有的(a1,a2,a3)的排列的N(a1,a2,a3)平均值为(
)
A.
B.
3
C.
D.
4
二 多项选择题∶本题共4小题,每小题5分,共20分,在每小题给出的选项中,有多项符合题目要求,全部选对的得5分,部分选对的得3分,有选错的得0分.
9.
已知为等差数列,其前项和为,且,则以下结论正确的是(
).
A.
B.
最小
C.
D.
10.
已知曲线的方程为,则下列结论正确的是(
)
A.
当时,曲线为椭圆,其焦距为
B.
当时,曲线为双曲线,其离心率为
C.
存在实数使得曲线为焦点在轴上双曲线
D.
当时,曲线为双曲线,其渐近线与圆相切
11.
设函数(),已知在有且仅有3个零点,下列结论正确的是(
)
A.
在上存在,,满足
B.
有且仅有1个最小值点
C.
在单调递增
D.
的取值范围是
12.
在三棱锥D-ABC中,,且,,M,N分别是棱BC,CD的中点,下面结论正确的是(
)
A.
B.
平面ABD
C.
三棱锥A-CMN的体积的最大值为
D.
AD与BC一定不垂直
三 填空题∶本题共4小题,每小题5分,共20分.
13.
左手掷一粒骰子,右手掷一枚硬币,则事件“骰子向上为6点且硬币向上为正面”的概率为_____.
14.
若展开式的二项式系数之和是,则__________;展开式中的常数项的值是__________.
15.
的内角、,的对边分别为、、,,已知向量,.若,则___________.
16.
设,分别是椭圆的左 右焦点,过的直线交椭圆于,两点,且,,则椭圆的离心率为_________
四 解答题∶本题共6小题,共70分.解答应写出文字说明 证明过程或演算步骤.
17.
在①,,成等差数列.②,,成等差数列中任选一个,补充在下列的问题中,并解答.
在公比为2的等比数列中,______
(1)求数列的通项公式;
(2)若,求数列的前n项和.
18.
设函数.
(1)若为函数的图像的一条对称轴,当时,求函数的最小值及相应的值;
(2)将函数的图象向左平移个单位得到函数的图像,已知,求的单调递减区间.
19.
如图,直三棱柱中,,,,点是的中点.
(1)求证∶平面;
(2)求与平面所成角的正弦值.
20.
移动支付(支付宝及微信支付)已经渐渐成为人们购物消费的一种支付方式,为调查市民使用移动支付的年龄结构,随机对100位市民做问卷调查得到2×2列联表如下∶
35岁以下(含35岁)
35岁以上
合计
使用移动支付
40
50
不使用移动支付
40
合计
100
(1)将上2×2列联表补充完整,并请说明在犯错误概率不超过0.10的前提下,认为支付方式与年龄是否有关?
(2)在使用移动支付的人群中采用分层抽样的方式抽取10人做进一步的问卷调查,从这10人随机中选出3人颁发参与奖励,设年龄都低于35岁(含35岁)的人数为X,求X的分布列及期望.
0.50
0.40
0.25
0.15
0.10
0.05
0.025
0.010
0.005
0.001
K
0.455
0.708
1.323
2.072
2.706
3.841
5.024
6.635
7.879
10.828
(参考公式:(其中n=a+b+c+d)
21.
已知椭圆的右焦点与抛物线焦点重合,且椭圆的离心率为,过轴正半轴一点且斜率为的直线交椭圆于两点.
(1)求椭圆的标准方程;
(2)是否存在实数使以线段为直径的圆经过点,若存在,求出实数的值;若不存在说明理由.
22.
已知函数 (为实常数).
(1)若,求曲线在处的切线方程;
(2)讨论函数在上的单调性;
(3)若存在,使得成立,求实数取值范围.
海口一中2021届高三数学9月月考试题
答案
一 单项选择题∶本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.
已知集合,,则(
)
A.
B.
C.
D.
答案:B
2.
已知为虚数单位,复数满足,则共轭复数为(
)
A.
B.
C.
D.
答案:C
3.
若,则(
)
A.
B.
C.
D.
答案:C
4.
已知,且,则的最小值为(
)
A.
B.
C.
D.
答案:C
5.
设,,,则(
)
A.
B.
C.
D.
答案:C
6.
已知抛物线的焦点为,准线为,是上一点,直线与抛物线交于,两点,若,则=
A.
B.
C.
D.
答案:B
7.
已知函数是定义在R上的奇函数,当时,,则使不等式成立的x的取值范围是(
)
A.
B.
C.
D.
答案:C
8.
已知a1,a2,a3∈{2,4,6},记N(a1,a2,a3)为a1,a2,a3中不同数字的个数,如∶N(2,2,2)=1,N(2,4,2)=2,N(2,4,6)=3,则所有的(a1,a2,a3)的排列的N(a1,a2,a3)平均值为(
)
A.
B.
3
C.
D.
4
答案:A
二 多项选择题∶本题共4小题,每小题5分,共20分,在每小题给出的选项中,有多项符合题目要求,全部选对的得5分,部分选对的得3分,有选错的得0分.
9.
已知为等差数列,其前项和为,且,则以下结论正确的是(
).
A.
B.
最小
C.
D.
答案:ACD
10.
已知曲线的方程为,则下列结论正确的是(
)
A.
当时,曲线为椭圆,其焦距为
B.
当时,曲线为双曲线,其离心率为
C.
存在实数使得曲线为焦点在轴上双曲线
D.
当时,曲线为双曲线,其渐近线与圆相切
答案:ABD
11.
设函数(),已知在有且仅有3个零点,下列结论正确的是(
)
A.
在上存在,,满足
B.
有且仅有1个最小值点
C.
在单调递增
D.
的取值范围是
答案:AB
12.
在三棱锥D-ABC中,,且,,M,N分别是棱BC,CD的中点,下面结论正确的是(
)
A.
B.
平面ABD
C.
三棱锥A-CMN的体积的最大值为
D.
AD与BC一定不垂直
答案:ABD
三 填空题∶本题共4小题,每小题5分,共20分.
13.
左手掷一粒骰子,右手掷一枚硬币,则事件“骰子向上为6点且硬币向上为正面”的概率为_____.
答案:
14.
若展开式的二项式系数之和是,则__________;展开式中的常数项的值是__________.
答案:
①.
②.
135
15.
的内角、,的对边分别为、、,,已知向量,.若,则___________.
答案:
16.
设,分别是椭圆的左 右焦点,过的直线交椭圆于,两点,且,,则椭圆的离心率为_________
答案:
四 解答题∶本题共6小题,共70分.解答应写出文字说明 证明过程或演算步骤.
17.
在①,,成等差数列.②,,成等差数列中任选一个,补充在下列的问题中,并解答.
在公比为2的等比数列中,______
(1)求数列的通项公式;
(2)若,求数列的前n项和.
答案:(1)(2)
18.
设函数.
(1)若为函数的图像的一条对称轴,当时,求函数的最小值及相应的值;
(2)将函数的图象向左平移个单位得到函数的图像,已知,求的单调递减区间.
答案:(1)当时,函数的最小值为;(2)单调递减区间为,.
19.
如图,直三棱柱中,,,,点是的中点.
(1)求证∶平面;
(2)求与平面所成角的正弦值.
答案:(1)证明见解析;(2).
20.
移动支付(支付宝及微信支付)已经渐渐成为人们购物消费的一种支付方式,为调查市民使用移动支付的年龄结构,随机对100位市民做问卷调查得到2×2列联表如下∶
35岁以下(含35岁)
35岁以上
合计
使用移动支付
40
50
不使用移动支付
40
合计
100
(1)将上2×2列联表补充完整,并请说明在犯错误概率不超过0.10的前提下,认为支付方式与年龄是否有关?
(2)在使用移动支付的人群中采用分层抽样的方式抽取10人做进一步的问卷调查,从这10人随机中选出3人颁发参与奖励,设年龄都低于35岁(含35岁)的人数为X,求X的分布列及期望.
0.50
0.40
0.25
0.15
0.10
0.05
0.025
0.010
0.005
0.001
K
0.455
0.708
1.323
2.072
2.706
3.841
5.024
6.635
7.879
10.828
(参考公式:(其中n=a+b+c+d)
答案:(1)列联表答案见解析,在犯错误的概率不超过0.10的前提下,认为支付方式与年龄有关;(2)分布列答案见解析,数学期望:.
21.
已知椭圆的右焦点与抛物线焦点重合,且椭圆的离心率为,过轴正半轴一点且斜率为的直线交椭圆于两点.
(1)求椭圆的标准方程;
(2)是否存在实数使以线段为直径的圆经过点,若存在,求出实数的值;若不存在说明理由.
答案:(1);(2)存在,.
22.
已知函数 (为实常数).
(1)若,求曲线在处的切线方程;
(2)讨论函数在上的单调性;
(3)若存在,使得成立,求实数取值范围.
答案:(1)y=1.(2)答案见解析;(3).
同课章节目录
