2021-2022学年人教版 九年级数学上册_24.1 圆的有关性质 巩固提升(word版含答案)
文档属性
| 名称 | 2021-2022学年人教版 九年级数学上册_24.1 圆的有关性质 巩固提升(word版含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 608.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-06 00:00:00 | ||
图片预览



文档简介
人教版
九年级数学上册
24.1
圆的有关性质
巩固提升
一、选择题
1.
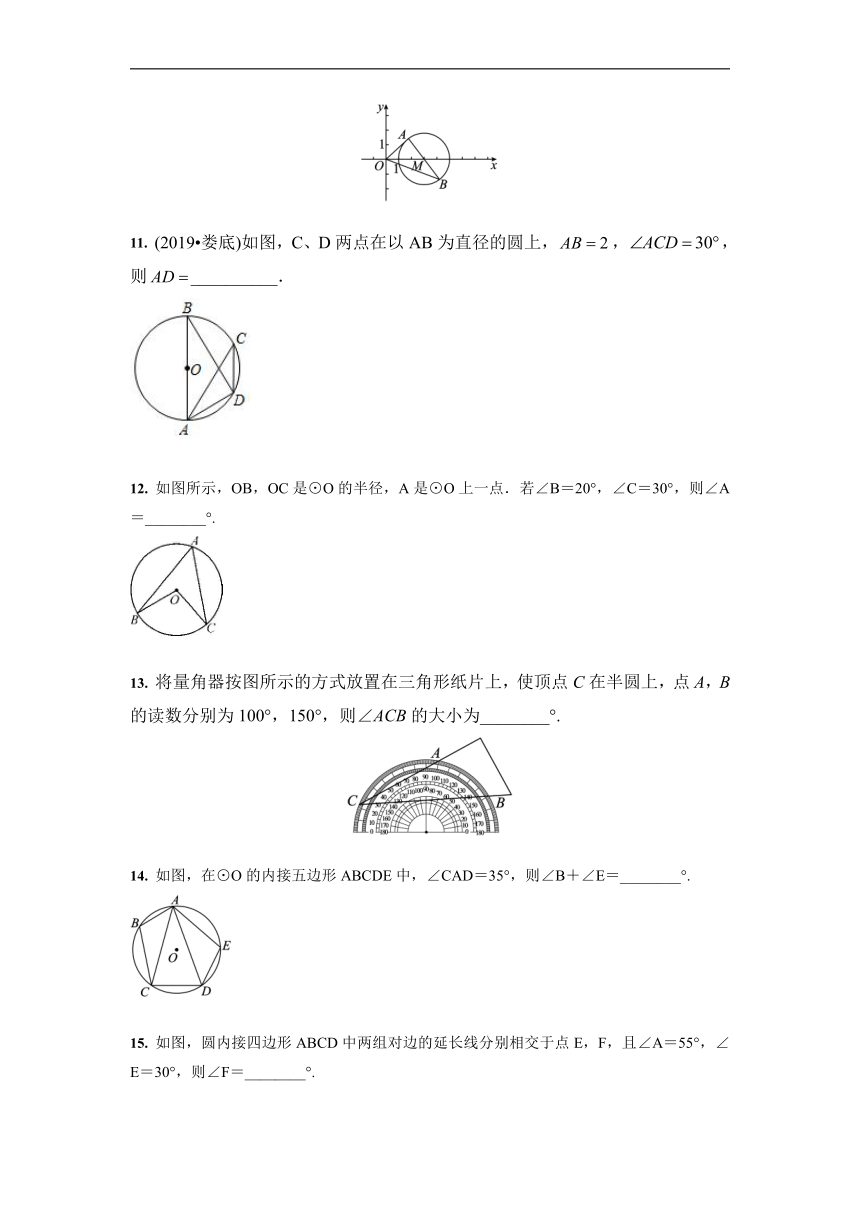
如图,⊙O过点B、C,圆心O在等腰直角△ABC的内部,∠BAC=90°,OA=1,BC=6,则⊙O的半径为( )
A.
B.
2
C.
D.
3
2.
如图,在⊙O中,∠ABC=50°,则∠AOC等于( )
A.
50°
B.
80°
C.
90°
D.
100°
3.
2019·葫芦岛
如图,在⊙O中,∠BAC=15°,∠ADC=20°,则∠ABO的度数为( )
A.70°
B.55°
C.45°
D.35°
4.
如图,AB是⊙O的直径,==,∠COD=34°,则∠AEO的度数是( )
A.51°
B.56°
C.68°
D.78°
5.
有下列说法:(1)直径是弦;(2)弦是直径;(3)半圆是弧,但弧不一定是半圆;(4)半径相等的两个圆是等圆;(5)长度相等的两条弧是等弧.其中错误的有( )
A.1个
B.2个
C.3个
D.4个
6.
如图,已知⊙O的半径为5,弦AB,CD所对的圆心角分别是∠AOB,∠COD,若∠AOB与∠COD互补,弦CD=6,则弦AB的长为( )
A.6
B.8
C.5
D.5
7.
甲、乙、丙三个牧民用同样长为l米的铁丝各围一块草地放牧,甲牧民围成面积为S1的圆形草地,乙牧民围成面积为S2的正方形草地,丙牧民围成面积为S3的矩形(不是正方形)草地,则下列结论正确的是( )
A.S1>S3>S2
B.S2>S1>S3
C.S3>S1>S2
D.S1>S2>S3
8.
如图,A,B,C,D是⊙O上的四个点,B是的中点,M是半径OD上任意一点.若∠BDC=40°,则∠AMB的度数不可能是( )
A.45°
B.60°
C.75°
D.85°
二、填空题
9.
如图,在⊙O中,A,B是圆上的两点,已知∠AOB=40°,直径CD∥AB,连接AC,则∠BAC=________度.
10.
如图,平面直角坐标系xOy中,点M的坐标为(3,0),⊙M的半径为2,过点M的直线与⊙M的交点分别为A,B,则△AOB的面积的最大值为________,此时A,B两点所在直线与x轴的夹角等于________°.
11.
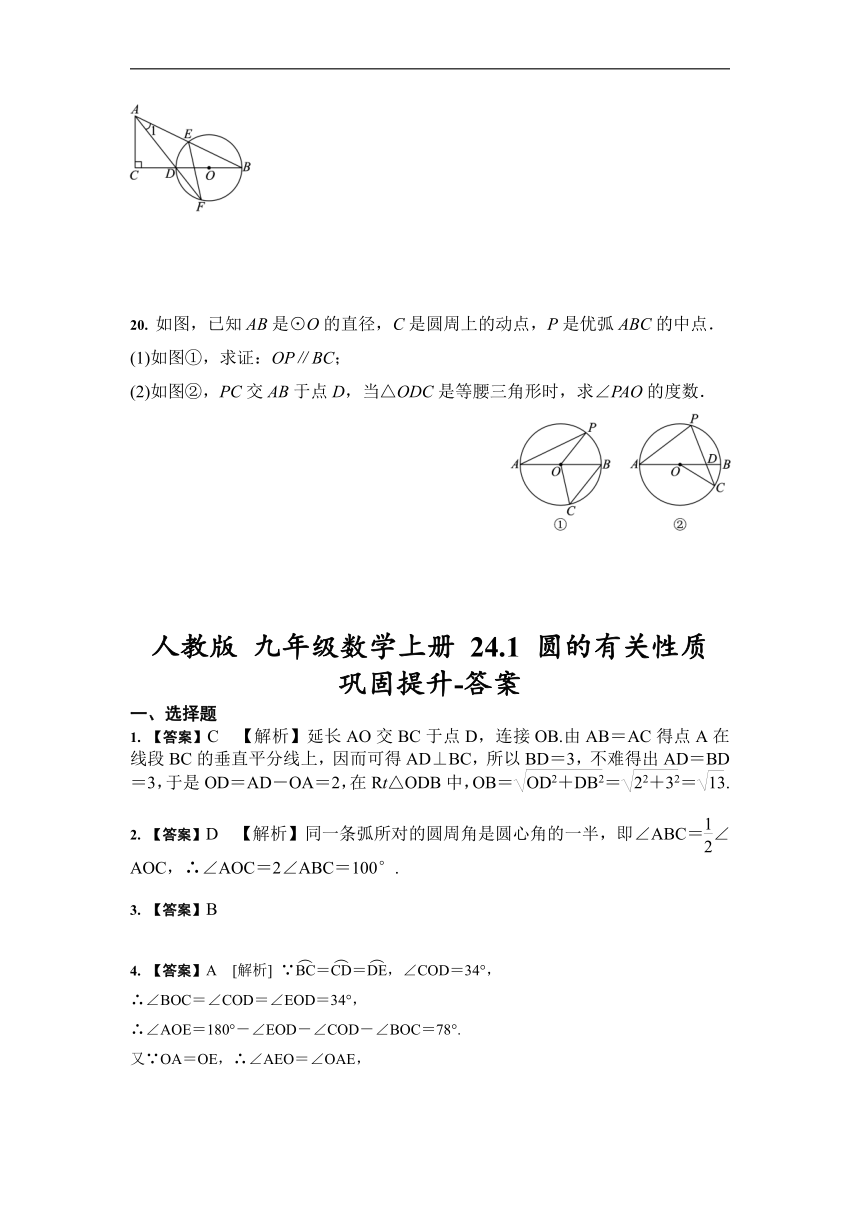
(2019 娄底)如图,C、D两点在以AB为直径的圆上,,,则__________.
12.
如图所示,OB,OC是⊙O的半径,A是⊙O上一点.若∠B=20°,∠C=30°,则∠A=________°.
13.
将量角器按图所示的方式放置在三角形纸片上,使顶点C在半圆上,点A,B的读数分别为100°,150°,则∠ACB的大小为________°.
14.
如图,在⊙O的内接五边形ABCDE中,∠CAD=35°,则∠B+∠E=________°.
15.
如图,圆内接四边形ABCD中两组对边的延长线分别相交于点E,F,且∠A=55°,∠E=30°,则∠F=________°.
16.
已知⊙O的半径为2,弦BC=2
,A是⊙O上一点,且=,直线AO与BC交于点D,则AD的长为________.
三、解答题
17.
如图,△ABC的高AD,BF相交于点H,AD的延长线交△ABC的外接圆于点E.求证:DH=DE.
18.
已知:如图5,在⊙O中,M,N分别为弦AB,CD的中点,AB=CD,AB不平行于CD.
求证:∠AMN=∠CNM.
19.
如图,在△ABC中,∠C=90°,D是BC边上一点,以BD为直径的⊙O经过AB的中点E,交AD的延长线于点F,连接EF.
(1)求证:∠1=∠F;
(2)若AC=4,EF=2
,求CD的长.
20.
如图,已知AB是⊙O的直径,C是圆周上的动点,P是优弧ABC的中点.
(1)如图①,求证:OP∥BC;
(2)如图②,PC交AB于点D,当△ODC是等腰三角形时,求∠PAO的度数.
人教版
九年级数学上册
24.1
圆的有关性质
巩固提升-答案
一、选择题
1.
【答案】C 【解析】延长AO交BC于点D,连接OB.由AB=AC得点A在线段BC的垂直平分线上,因而可得AD⊥BC,所以BD=3,不难得出AD=BD=3,于是OD=AD-OA=2,在Rt△ODB中,OB===.
2.
【答案】D 【解析】同一条弧所对的圆周角是圆心角的一半,即∠ABC=∠AOC,∴∠AOC=2∠ABC=100°.
3.
【答案】B
4.
【答案】A [解析]
∵==,∠COD=34°,
∴∠BOC=∠COD=∠EOD=34°,
∴∠AOE=180°-∠EOD-∠COD-∠BOC=78°.
又∵OA=OE,∴∠AEO=∠OAE,
∴∠AEO=×(180°-78°)=51°.
5.
【答案】B
6.
【答案】B [解析]
如图,延长AO交⊙O于点E,连接BE,
则∠AOB+∠BOE=180°.
又∵∠AOB+∠COD=180°,
∴∠BOE=∠COD,
∴BE=CD=6.
∵AE为⊙O的直径,∴∠ABE=90°,
∴AB==8.
7.
【答案】D [解析]
本题中甲的草地:2πr=l,r=,S1=π·r2=;乙的草地:S2=×=;丙的草地:设一边长为x,则S3=x(-x)=-x2+x.只有当x=时,S3取得最大值,此时S3=,但此时矩形为正方形,不符合题意.所以S1>S2>S3.
8.
【答案】D [解析]
连接AD,OA,OB.∵B是的中点,∴∠ADB=∠BDC=40°,∴∠AOB=2∠ADB=80°.又∵M是OD上一点,∴∠ADB≤∠AMB≤∠AOB,即40°≤∠AMB≤80°,则不符合条件的只有85°.
二、填空题
9.
【答案】35 【解析】∵OA=OB=OC,∴∠OAB=∠B,∠C=∠OAC,∵∠AOB=40°,∴∠B=∠OAB=70°,∵CD∥AB,∴∠BAC=∠C,∴∠OAC=∠BAC=∠OAB=35°.
10.
【答案】6 90 [解析]
∵AB为⊙M的直径,
∴AB=4.
当点O到AB的距离最大时,△AOB的面积最大,此时AB⊥x轴于点M,
∴△AOB的面积的最大值为×4×3=6,∠AMO=90°.
即此时A,B两点所在直线与x轴的夹角等于90°.
11.
【答案】1
【解析】∵AB为直径,∴,∵,∴.
故答案为:1.
12.
【答案】50 [解析]
连接OA,则OA=OB,OA=OC,
∴∠OAB=∠B,∠OAC=∠C,
∴∠BAC=∠OAB+∠OAC=∠B+∠C=20°+30°=50°.
13.
【答案】25 [解析]
设量角器的中心为O,由题意可得∠AOB=150°-100°=50°,
所以∠ACB=∠AOB=25°.
14.
【答案】215 [解析]
连接CE,则∠B+∠AEC=180°,∠DEC=∠CAD=35°,∴∠B+∠AED=(∠B+∠AEC)+∠DEC=180°+35°=215°.
15.
【答案】40 [解析]
∵∠BCD=180°-∠A=125°,∠CBF=∠A+∠E=85°,∴∠F=∠BCD-∠CBF=125°-85°=40°.
16.
【答案】3或1 [解析]
如图所示:
∵⊙O的半径为2,弦BC=2
,A是⊙O上一点,且=,
∴AO⊥BC,垂足为D,
则BD=BC=.
在Rt△OBD中,
∵BD2+OD2=OB2,
即()2+OD2=22,
解得OD=1.
∴当点A在如图①所示的位置时,AD=OA-OD=2-1=1;
当点A在如图②所示的位置时,AD=OA+OD=2+1=3.
三、解答题
17.
【答案】
证明:连接BE.
∵AD,BF是△ABC的高,
∴∠FBC+∠C=90°,∠CAD+∠C=90°,
∴∠FBC=∠CAD.
∵∠CBE=∠CAD,∴∠FBC=∠CBE.
又∵BD=BD,∠BDH=∠BDE=90°,
∴△BDH≌△BDE,∴DH=DE.
18.
【答案】
证明:连接OM,ON,OA,OC,如图所示.
∵M,N分别为AB,CD的中点,
∴OM⊥AB,ON⊥CD,AM=AB,CN=CD.
又∵AB=CD,∴AM=CN.
在Rt△AOM和Rt△CON中,
∴Rt△AOM≌Rt△CON(HL),
∴OM=ON,∴∠OMN=∠ONM,
∴∠AMO+∠OMN=∠CNO+∠ONM,
即∠AMN=∠CNM.
19.
【答案】
解:(1)证明:如图,连接DE.
∵BD是⊙O的直径,
∴∠DEB=90°,即DE⊥AB.
又∵E是AB的中点,
∴AD=BD,∴∠1=∠B.
又∵∠B=∠F,∴∠1=∠F.
(2)∵∠1=∠F,∴AE=EF=2
,
∴AB=2AE=4
.
在Rt△ABC中,∵AC=4,∠C=90°,
∴BC==8.
设CD=x,则AD=BD=8-x.
在Rt△ACD中,∵∠C=90°,
∴AC2+CD2=AD2,即42+x2=(8-x)2,
解得x=3,即CD=3.
20.
【答案】
解:(1)证明:如图①,连接PC.
∵=,∴∠AOP=∠COP.
在△AOP和△COP中,
∴△AOP≌△COP,∴∠APO=∠CPO.
∵OA=OP,∴∠APO=∠OAP.
又∵∠PCB=∠OAP,
∴∠CPO=∠PCB,
∴OP∥BC.
(2)如图②,连接OP,AC.
∵=,∴PA=PC,∴∠PAC=∠PCA.
∵OA=OC,∴∠OAC=∠OCA,
∴∠PAO=∠PCO.
当DO=DC时,设∠DCO=x,
则∠DOC=x,∠PAO=x,
∴∠OPC=∠OCP=x,∠PDO=2x.
∵∠PAO=x,∴∠POD=2∠PAO=2x.
在△POD中,x+2x+2x=180°,解得x=36°,
即∠PAO=36°.
当CO=CD时,设∠DCO=x,
则∠OPC=x,∠PAO=x,
∴∠POD=2x,
∴∠ODC=∠POD+∠OPC=2x+x=3x.
∵CD=CO,
∴∠DOC=∠ODC=3x.
在△POC中,x+x+5x=180°,
解得x=(),即∠PAO=()°,).
当OC=OD时,B,D重合,不符合题意,舍去.
综上所述,∠PAO的度数为36°或()°,).
九年级数学上册
24.1
圆的有关性质
巩固提升
一、选择题
1.
如图,⊙O过点B、C,圆心O在等腰直角△ABC的内部,∠BAC=90°,OA=1,BC=6,则⊙O的半径为( )
A.
B.
2
C.
D.
3
2.
如图,在⊙O中,∠ABC=50°,则∠AOC等于( )
A.
50°
B.
80°
C.
90°
D.
100°
3.
2019·葫芦岛
如图,在⊙O中,∠BAC=15°,∠ADC=20°,则∠ABO的度数为( )
A.70°
B.55°
C.45°
D.35°
4.
如图,AB是⊙O的直径,==,∠COD=34°,则∠AEO的度数是( )
A.51°
B.56°
C.68°
D.78°
5.
有下列说法:(1)直径是弦;(2)弦是直径;(3)半圆是弧,但弧不一定是半圆;(4)半径相等的两个圆是等圆;(5)长度相等的两条弧是等弧.其中错误的有( )
A.1个
B.2个
C.3个
D.4个
6.
如图,已知⊙O的半径为5,弦AB,CD所对的圆心角分别是∠AOB,∠COD,若∠AOB与∠COD互补,弦CD=6,则弦AB的长为( )
A.6
B.8
C.5
D.5
7.
甲、乙、丙三个牧民用同样长为l米的铁丝各围一块草地放牧,甲牧民围成面积为S1的圆形草地,乙牧民围成面积为S2的正方形草地,丙牧民围成面积为S3的矩形(不是正方形)草地,则下列结论正确的是( )
A.S1>S3>S2
B.S2>S1>S3
C.S3>S1>S2
D.S1>S2>S3
8.
如图,A,B,C,D是⊙O上的四个点,B是的中点,M是半径OD上任意一点.若∠BDC=40°,则∠AMB的度数不可能是( )
A.45°
B.60°
C.75°
D.85°
二、填空题
9.
如图,在⊙O中,A,B是圆上的两点,已知∠AOB=40°,直径CD∥AB,连接AC,则∠BAC=________度.
10.
如图,平面直角坐标系xOy中,点M的坐标为(3,0),⊙M的半径为2,过点M的直线与⊙M的交点分别为A,B,则△AOB的面积的最大值为________,此时A,B两点所在直线与x轴的夹角等于________°.
11.
(2019 娄底)如图,C、D两点在以AB为直径的圆上,,,则__________.
12.
如图所示,OB,OC是⊙O的半径,A是⊙O上一点.若∠B=20°,∠C=30°,则∠A=________°.
13.
将量角器按图所示的方式放置在三角形纸片上,使顶点C在半圆上,点A,B的读数分别为100°,150°,则∠ACB的大小为________°.
14.
如图,在⊙O的内接五边形ABCDE中,∠CAD=35°,则∠B+∠E=________°.
15.
如图,圆内接四边形ABCD中两组对边的延长线分别相交于点E,F,且∠A=55°,∠E=30°,则∠F=________°.
16.
已知⊙O的半径为2,弦BC=2
,A是⊙O上一点,且=,直线AO与BC交于点D,则AD的长为________.
三、解答题
17.
如图,△ABC的高AD,BF相交于点H,AD的延长线交△ABC的外接圆于点E.求证:DH=DE.
18.
已知:如图5,在⊙O中,M,N分别为弦AB,CD的中点,AB=CD,AB不平行于CD.
求证:∠AMN=∠CNM.
19.
如图,在△ABC中,∠C=90°,D是BC边上一点,以BD为直径的⊙O经过AB的中点E,交AD的延长线于点F,连接EF.
(1)求证:∠1=∠F;
(2)若AC=4,EF=2
,求CD的长.
20.
如图,已知AB是⊙O的直径,C是圆周上的动点,P是优弧ABC的中点.
(1)如图①,求证:OP∥BC;
(2)如图②,PC交AB于点D,当△ODC是等腰三角形时,求∠PAO的度数.
人教版
九年级数学上册
24.1
圆的有关性质
巩固提升-答案
一、选择题
1.
【答案】C 【解析】延长AO交BC于点D,连接OB.由AB=AC得点A在线段BC的垂直平分线上,因而可得AD⊥BC,所以BD=3,不难得出AD=BD=3,于是OD=AD-OA=2,在Rt△ODB中,OB===.
2.
【答案】D 【解析】同一条弧所对的圆周角是圆心角的一半,即∠ABC=∠AOC,∴∠AOC=2∠ABC=100°.
3.
【答案】B
4.
【答案】A [解析]
∵==,∠COD=34°,
∴∠BOC=∠COD=∠EOD=34°,
∴∠AOE=180°-∠EOD-∠COD-∠BOC=78°.
又∵OA=OE,∴∠AEO=∠OAE,
∴∠AEO=×(180°-78°)=51°.
5.
【答案】B
6.
【答案】B [解析]
如图,延长AO交⊙O于点E,连接BE,
则∠AOB+∠BOE=180°.
又∵∠AOB+∠COD=180°,
∴∠BOE=∠COD,
∴BE=CD=6.
∵AE为⊙O的直径,∴∠ABE=90°,
∴AB==8.
7.
【答案】D [解析]
本题中甲的草地:2πr=l,r=,S1=π·r2=;乙的草地:S2=×=;丙的草地:设一边长为x,则S3=x(-x)=-x2+x.只有当x=时,S3取得最大值,此时S3=,但此时矩形为正方形,不符合题意.所以S1>S2>S3.
8.
【答案】D [解析]
连接AD,OA,OB.∵B是的中点,∴∠ADB=∠BDC=40°,∴∠AOB=2∠ADB=80°.又∵M是OD上一点,∴∠ADB≤∠AMB≤∠AOB,即40°≤∠AMB≤80°,则不符合条件的只有85°.
二、填空题
9.
【答案】35 【解析】∵OA=OB=OC,∴∠OAB=∠B,∠C=∠OAC,∵∠AOB=40°,∴∠B=∠OAB=70°,∵CD∥AB,∴∠BAC=∠C,∴∠OAC=∠BAC=∠OAB=35°.
10.
【答案】6 90 [解析]
∵AB为⊙M的直径,
∴AB=4.
当点O到AB的距离最大时,△AOB的面积最大,此时AB⊥x轴于点M,
∴△AOB的面积的最大值为×4×3=6,∠AMO=90°.
即此时A,B两点所在直线与x轴的夹角等于90°.
11.
【答案】1
【解析】∵AB为直径,∴,∵,∴.
故答案为:1.
12.
【答案】50 [解析]
连接OA,则OA=OB,OA=OC,
∴∠OAB=∠B,∠OAC=∠C,
∴∠BAC=∠OAB+∠OAC=∠B+∠C=20°+30°=50°.
13.
【答案】25 [解析]
设量角器的中心为O,由题意可得∠AOB=150°-100°=50°,
所以∠ACB=∠AOB=25°.
14.
【答案】215 [解析]
连接CE,则∠B+∠AEC=180°,∠DEC=∠CAD=35°,∴∠B+∠AED=(∠B+∠AEC)+∠DEC=180°+35°=215°.
15.
【答案】40 [解析]
∵∠BCD=180°-∠A=125°,∠CBF=∠A+∠E=85°,∴∠F=∠BCD-∠CBF=125°-85°=40°.
16.
【答案】3或1 [解析]
如图所示:
∵⊙O的半径为2,弦BC=2
,A是⊙O上一点,且=,
∴AO⊥BC,垂足为D,
则BD=BC=.
在Rt△OBD中,
∵BD2+OD2=OB2,
即()2+OD2=22,
解得OD=1.
∴当点A在如图①所示的位置时,AD=OA-OD=2-1=1;
当点A在如图②所示的位置时,AD=OA+OD=2+1=3.
三、解答题
17.
【答案】
证明:连接BE.
∵AD,BF是△ABC的高,
∴∠FBC+∠C=90°,∠CAD+∠C=90°,
∴∠FBC=∠CAD.
∵∠CBE=∠CAD,∴∠FBC=∠CBE.
又∵BD=BD,∠BDH=∠BDE=90°,
∴△BDH≌△BDE,∴DH=DE.
18.
【答案】
证明:连接OM,ON,OA,OC,如图所示.
∵M,N分别为AB,CD的中点,
∴OM⊥AB,ON⊥CD,AM=AB,CN=CD.
又∵AB=CD,∴AM=CN.
在Rt△AOM和Rt△CON中,
∴Rt△AOM≌Rt△CON(HL),
∴OM=ON,∴∠OMN=∠ONM,
∴∠AMO+∠OMN=∠CNO+∠ONM,
即∠AMN=∠CNM.
19.
【答案】
解:(1)证明:如图,连接DE.
∵BD是⊙O的直径,
∴∠DEB=90°,即DE⊥AB.
又∵E是AB的中点,
∴AD=BD,∴∠1=∠B.
又∵∠B=∠F,∴∠1=∠F.
(2)∵∠1=∠F,∴AE=EF=2
,
∴AB=2AE=4
.
在Rt△ABC中,∵AC=4,∠C=90°,
∴BC==8.
设CD=x,则AD=BD=8-x.
在Rt△ACD中,∵∠C=90°,
∴AC2+CD2=AD2,即42+x2=(8-x)2,
解得x=3,即CD=3.
20.
【答案】
解:(1)证明:如图①,连接PC.
∵=,∴∠AOP=∠COP.
在△AOP和△COP中,
∴△AOP≌△COP,∴∠APO=∠CPO.
∵OA=OP,∴∠APO=∠OAP.
又∵∠PCB=∠OAP,
∴∠CPO=∠PCB,
∴OP∥BC.
(2)如图②,连接OP,AC.
∵=,∴PA=PC,∴∠PAC=∠PCA.
∵OA=OC,∴∠OAC=∠OCA,
∴∠PAO=∠PCO.
当DO=DC时,设∠DCO=x,
则∠DOC=x,∠PAO=x,
∴∠OPC=∠OCP=x,∠PDO=2x.
∵∠PAO=x,∴∠POD=2∠PAO=2x.
在△POD中,x+2x+2x=180°,解得x=36°,
即∠PAO=36°.
当CO=CD时,设∠DCO=x,
则∠OPC=x,∠PAO=x,
∴∠POD=2x,
∴∠ODC=∠POD+∠OPC=2x+x=3x.
∵CD=CO,
∴∠DOC=∠ODC=3x.
在△POC中,x+x+5x=180°,
解得x=(),即∠PAO=()°,).
当OC=OD时,B,D重合,不符合题意,舍去.
综上所述,∠PAO的度数为36°或()°,).
同课章节目录
