2020-2021学年八年级数学鲁教版下册《9.2平行线分线段成比例》同步提升训练 (word版含答案)
文档属性
| 名称 | 2020-2021学年八年级数学鲁教版下册《9.2平行线分线段成比例》同步提升训练 (word版含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 371.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-06 00:00:00 | ||
图片预览


文档简介
2021学年鲁教版八年级数学下册《9.2平行线分线段成比例》同步提升训练(附答案)
一、单选题
1.如图,在△ABC中,D是BC上一点,连接AD,,F是AD的中点,连接BF并延长交AC于E,则的值是( )
A.
B.
C.
D.
2.如图,已知直线a∥b∥c,直线m,n与a,b,c分别交于点A,C,E,B,D,F,若AC=4,CE=6,BD=3,则DF的值是( )
A.4
B.4.5
C.5
D.5.5
3.如图,在△ABC中,DE∥BC,若=,则=( )
A.
B.
C.
D.
4.如图,l1∥l2∥l3,根据“平行线分线段成比例定理”,下列比例式中正确的是( )
A.
B.
C.
D.
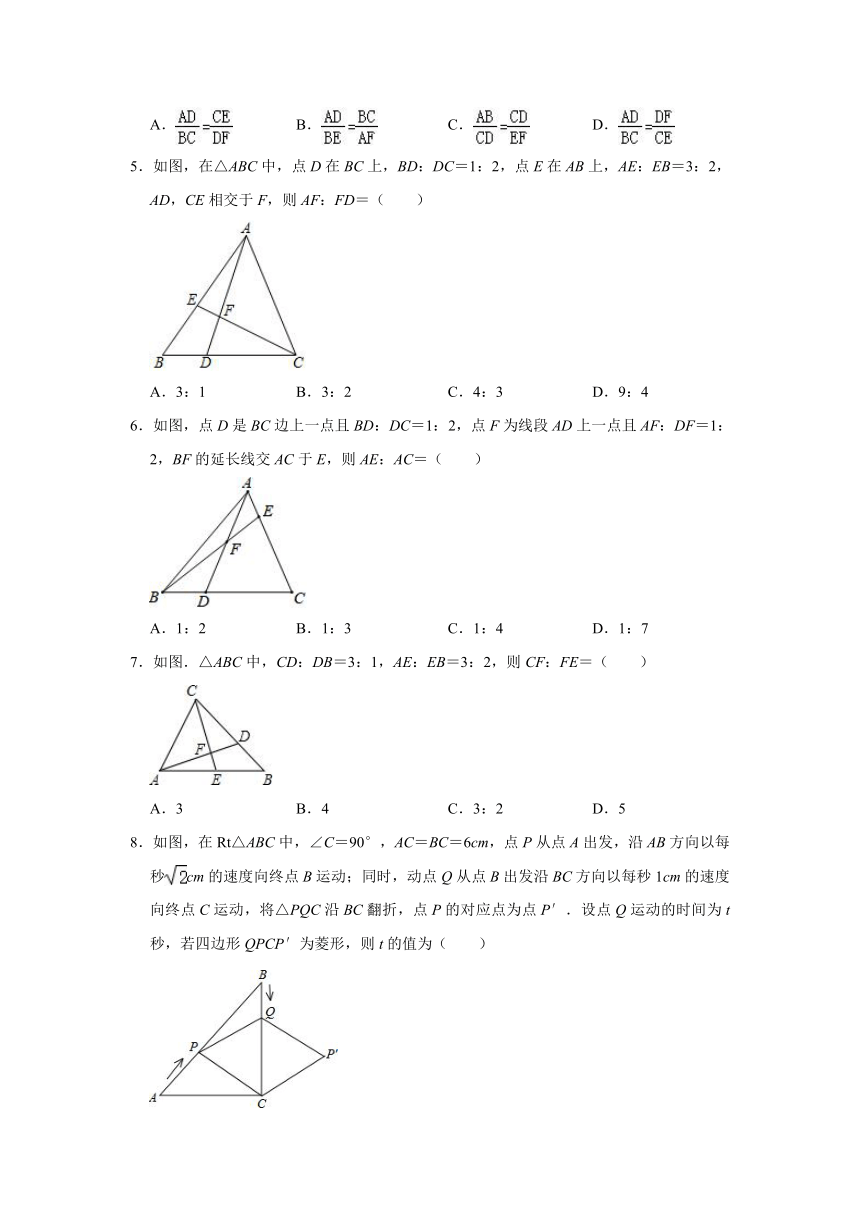
5.如图,在△ABC中,点D在BC上,BD:DC=1:2,点E在AB上,AE:EB=3:2,AD,CE相交于F,则AF:FD=( )
A.3:1
B.3:2
C.4:3
D.9:4
6.如图,点D是BC边上一点且BD:DC=1:2,点F为线段AD上一点且AF:DF=1:2,BF的延长线交AC于E,则AE:AC=( )
A.1:2
B.1:3
C.1:4
D.1:7
7.如图.△ABC中,CD:DB=3:1,AE:EB=3:2,则CF:FE=( )
A.3
B.4
C.3:2
D.5
8.如图,在Rt△ABC中,∠C=90°,AC=BC=6cm,点P从点A出发,沿AB方向以每秒cm的速度向终点B运动;同时,动点Q从点B出发沿BC方向以每秒1cm的速度向终点C运动,将△PQC沿BC翻折,点P的对应点为点P′.设点Q运动的时间为t秒,若四边形QPCP′为菱形,则t的值为( )
A.
B.2
C.
D.3
9.如图,l1∥l2∥l3,则下列等式错误的是( )
A.
B.
C.
D.
二、填空题
10.如图,直线l1∥l2,AF:FB=2:3,BC:CD=2:1,则AE:EC是
.
11.如图,AD为△ABC的中线,AE=AD,BE交AC于点F,DH∥BF,则=
.
12.如图,在Rt△ABC中,∠ACB=90°,AB=4,点D,E分别在边AB,AC上,且DB=2AD,AE=3EC,连接BE,CD,相交于点O,则△ABO面积最大值为
.
13.如图,直线l1∥l2∥l3,等腰Rt△ABC的三个顶点A、B、C分别在直线l1、l2、l3上,∠ACB=90°,AC交l2于点D.若l1与l2的距离为1,l1与l3的距离为4,则的值是
.
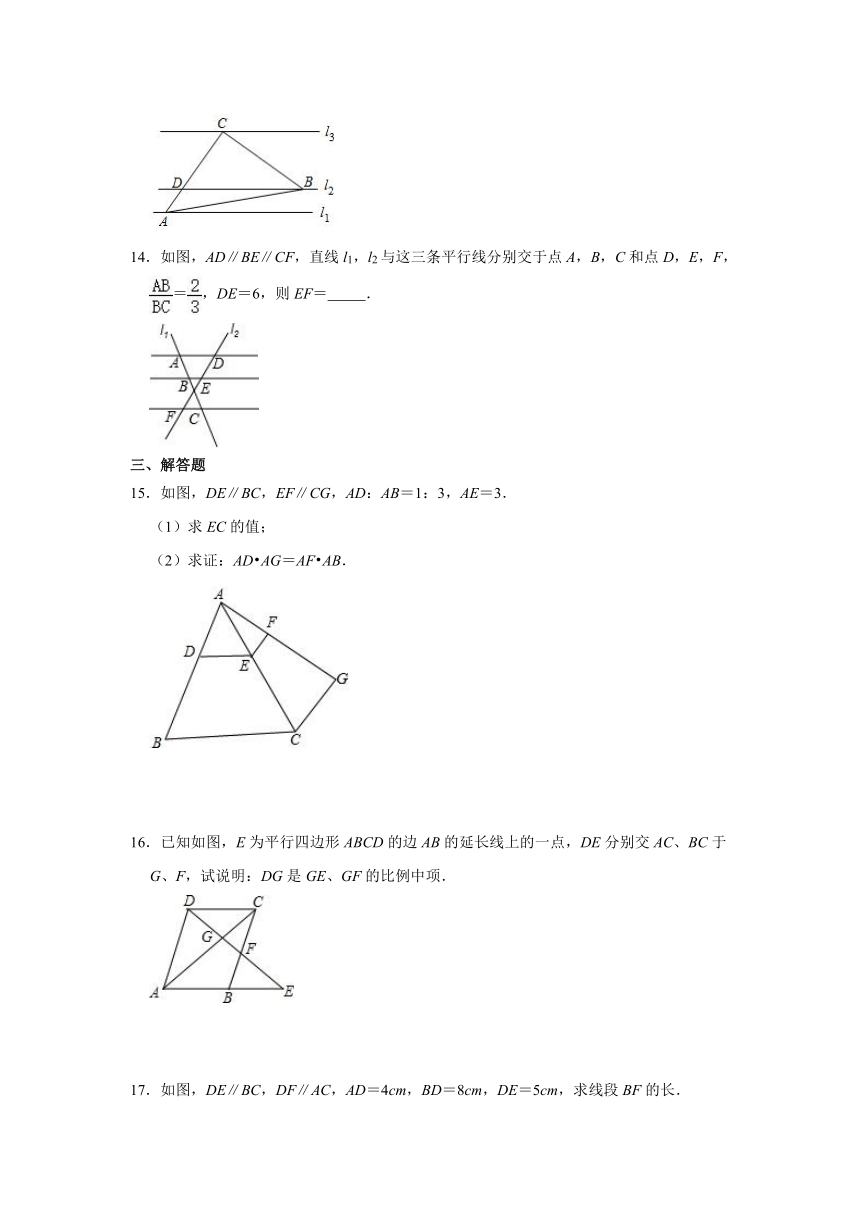
14.如图,AD∥BE∥CF,直线l1,l2与这三条平行线分别交于点A,B,C和点D,E,F,=,DE=6,则EF=
.
三、解答题
15.如图,DE∥BC,EF∥CG,AD:AB=1:3,AE=3.
(1)求EC的值;
(2)求证:AD AG=AF AB.
16.已知如图,E为平行四边形ABCD的边AB的延长线上的一点,DE分别交AC、BC于G、F,试说明:DG是GE、GF的比例中项.
17.如图,DE∥BC,DF∥AC,AD=4cm,BD=8cm,DE=5cm,求线段BF的长.
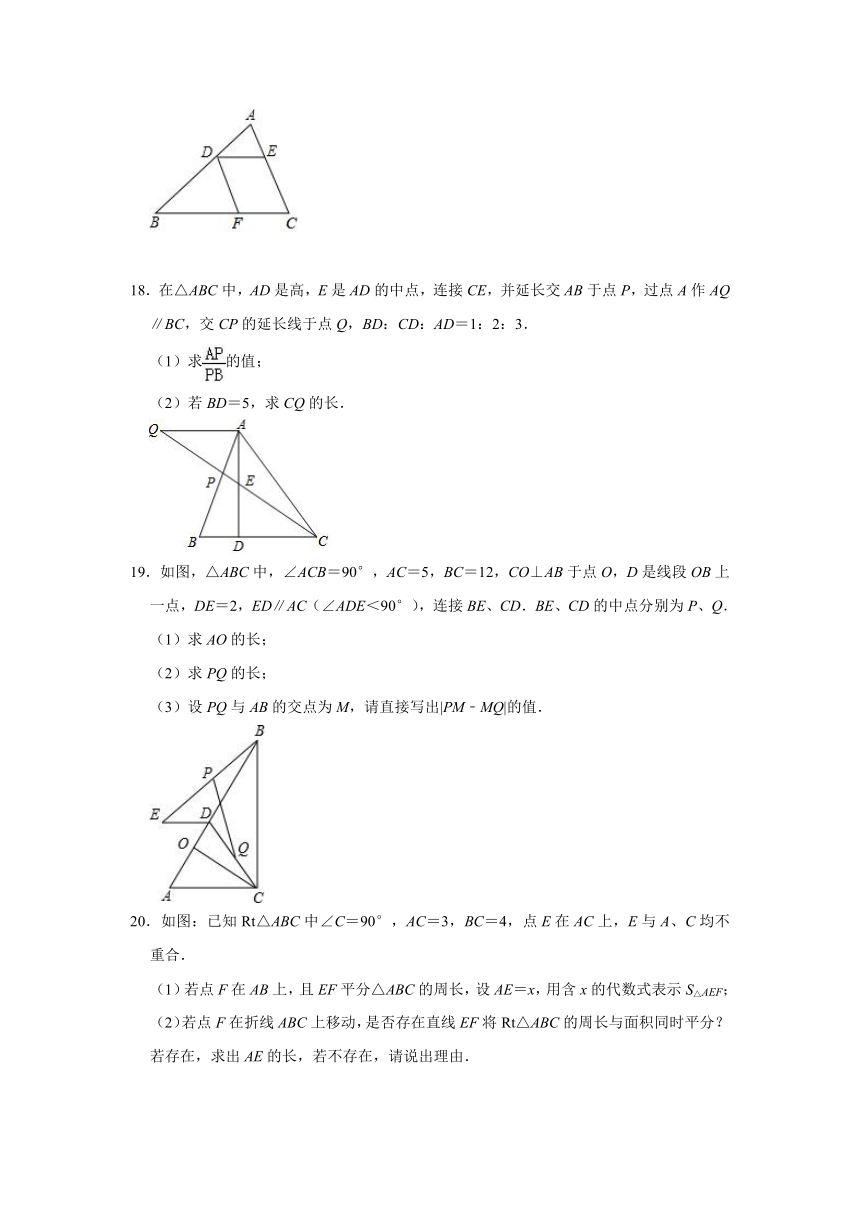
18.在△ABC中,AD是高,E是AD的中点,连接CE,并延长交AB于点P,过点A作AQ∥BC,交CP的延长线于点Q,BD:CD:AD=1:2:3.
(1)求的值;
(2)若BD=5,求CQ的长.
19.如图,△ABC中,∠ACB=90°,AC=5,BC=12,CO⊥AB于点O,D是线段OB上一点,DE=2,ED∥AC(∠ADE<90°),连接BE、CD.BE、CD的中点分别为P、Q.
(1)求AO的长;
(2)求PQ的长;
(3)设PQ与AB的交点为M,请直接写出|PM﹣MQ|的值.
20.如图:已知Rt△ABC中∠C=90°,AC=3,BC=4,点E在AC上,E与A、C均不重合.
(1)若点F在AB上,且EF平分△ABC的周长,设AE=x,用含x的代数式表示S△AEF;
(2)若点F在折线ABC上移动,是否存在直线EF将Rt△ABC的周长与面积同时平分?若存在,求出AE的长,若不存在,请说出理由.
参考答案
1.解:过D点作DH∥BE交AC于H,如图,
∵F点为AD的中点,
∴AF=FD,
∵FE∥DH,
∴==1,即AE=EH,
∵DH∥BE,
∴==,CH=3EH,
∴=.
故选:A.
2.解:∵直线a∥b∥c,AC=4,CE=6,BD=3,
∴=,即=,解得DF=4.5.
故选:B.
3.解:∵DE∥BC,
∴==,
故选:C.
4.解:∵l1∥l2∥l3,
∴=,A错误;
=,B错误;
≠,C错误;
=,D正确.
故选:D.
5.解:过点D作DH∥CE交AB于H,
则==,
∵=,
∴=,
∵DH∥CE,
∴==,
∴AF:FD=9:4,
故选:D.
6.解:如图,过A作BC的平行线,交BE的延长线于G,
∵AG∥BD,
∴△AFG∽△DFB,
∴==,
即2AG=BD,
又∵BD:DC=1:2,
∴CD=2BD=4AG,
∴BC=6AG,
∵AG∥BC,
∴△AEG∽△CEB,
∴==,
∴CE=6AE,
∴=,
故选:D.
7.解:过点D作DK∥AB交CE于K,
∵CD:DB=3:1,AE:EB=3:2,
∴CK:KE=CD:DB=3:1,DK:BE=3:4,
∵AE:EB=3:2,
∴DK:AE=1:2,
∴KF:EF=DK:AE=1:2,
∴CF:EF=5.
故选:D.
8.解:连接PP′交BC于O,
∵若四边形QPCP′为菱形,
∴PP′⊥QC,
∴∠POQ=90°,
∵∠ACB=90°,
∴PO∥AC,
∴=,
∵设点Q运动的时间为t秒,
∴AP=t,QB=t,
∴QC=6﹣t,
∴CO=3﹣,
∵AC=CB=6,∠ACB=90°,
∴AB=6,
∴=,
解得:t=2,
故选:B.
9.解:∵l1∥l2∥l3,
∴,,,,
∴A、B、C都正确,D错误.
故选:D.
10.解:∵直线l1∥l2,
∴=,,
∵BC:CD=2:1,
∴=2,
∴AE:EC=2:1.
故答案为:2:1.
11.解:∵DH∥BF,AD为△ABC的中线,
∴CH=FH,
∵DH∥BF,AE=AD,
∴AF=FH,
∴=,
故答案为:.
12.解:如图,过点D作DF∥AE,
则==,
∵=,
∴DF=2EC,
∴DO=2OC,
∴DO=DC,
∴S△ADO=S△ADC,S△BDO=S△BDC,
∴S△ABO=S△ABC,
∵∠ACB=90°,
∴C在以AB为直径的圆上,设圆心为G,
当CG⊥AB时,△ABC的面积最大为:4×2=4,
此时△ABO的面积最大为:×4=.
故答案为:.
13.解:作AE⊥l3于E,交l2于F,作BH⊥l3于H,如图,
∵l1∥l2∥l3,
∴AF⊥l2,
∴EF=BH=3,AF=1,
∵△ABC为等腰直角三角形,
∴AC=BC,
∵∠ACB=90°,
∴∠ACE+∠CAE=90°,
∴∠ACE+∠BCH=90°,
∴∠CAE=∠BCH,
在△ACE和△CBH中,
,
∴△ACE≌△CBH(AAS),
∴CE=BH=3,
在Rt△ACE中,AC==5,
∴AB=AC=5,
∵DF∥CE,
∴==,
∴CD=,
在Rt△BCD中,BD==,
∴==.
故答案为.
14.解:∵AD∥BE∥CF,
∴=,即=,
∴EF=9.
故答案为9.
15.(1)解:
∵DE∥BC,
∴=,
又=,AE=3,
∴=,
解得AC=9,
∴EC=AC﹣AE=9﹣3=6;
(2)证明:
∵DE∥BC,EF∥CG,
∴==,
∴AD AG=AF AB.
16.解:∵四边形ABCD是平行四边形,
∴DC∥AE,
∴=,
∵AD∥BC,
∴=,
∴=,
∴DG2=GE GF,
∴DG是GE、GF的比例中项.
17.解:∵DE∥BC,DF∥AC,
∴四边形DECF是平行四边形,
∴FC=DE=5
cm.
∵DF∥AC,
∴
即
∴BF=10(cm).
18.解:(1)设BD=x,则CD=2x,AD=3x,BC=BD+CD=3x,
∵AQ∥BC,
∴==1,
∴AQ=CD=2x,
∴==;
(2)∵BD=5,BD:CD:AD=1:2:3,
∴CD=10,AD=15,
∵E是AD的中点,
∴DE=AD=7.5,
由勾股定理得,CE==,
∴CQ=25.
19.解:(1)如图1中,
∵CO⊥AB,
∴∠AOC=∠ACB=90°,∵∠A=∠A,
∴△ABC∽△ACO,
∴=,
∵AB===13,
∴OA==.
(2)如图2中,取BD中点F,CD中点Q,连接PF、QF,
则PF∥ED,FQ∥BC,PF⊥FQ,且PF=ED=1,FQ=BC=6,
在Rt△PFQ中,PQ===.
(3)如图3中,取AD中点G,连接GQ,
∵GQ∥AC,ED∥AC,PF∥ED,
∴PF∥GQ,
∴△PMF∽△QMG,
∴==,
∵PM+QM=,
∴PM=,MQ=,
∴|PM﹣QM|=.
20.解:(1)过点F作FM⊥AC于M,
EF平分△ABC的周长,AE=x,所以可得AE+AF=CE+BC+BF,
即:x+AF=3﹣x+4+5﹣AF,解得AF=6﹣x.
由平行线分线段成比例定理可知,
AF:AB=FM:BC,即,6﹣x:5=FM:4,
解得FM=,
所以S△AEF==
(2)若EF存在,
①当F在AB上时,如图1,
则由(1)可知,S△AEF==×=3,
化简得,2x2﹣12x+15=0,由△=122﹣4×2×15=24>0,
解得x1=,x2=(不合题意舍去).
即AE=.
②当F在BC上时,如图2,
CF+CE=AE+AB+BF,
即CF+3﹣x=x+5+4﹣CF,
CF=3+x,
根据面积平分得出S△CFE=S四边形BFEA=S△ACB=3,
即×(3﹣x)×(3+x)=3,
解得:x3=(舍弃),x4=﹣(舍去),
即存在直线EF将Rt△ABC的周长与面积同时平分,AE的长是
一、单选题
1.如图,在△ABC中,D是BC上一点,连接AD,,F是AD的中点,连接BF并延长交AC于E,则的值是( )
A.
B.
C.
D.
2.如图,已知直线a∥b∥c,直线m,n与a,b,c分别交于点A,C,E,B,D,F,若AC=4,CE=6,BD=3,则DF的值是( )
A.4
B.4.5
C.5
D.5.5
3.如图,在△ABC中,DE∥BC,若=,则=( )
A.
B.
C.
D.
4.如图,l1∥l2∥l3,根据“平行线分线段成比例定理”,下列比例式中正确的是( )
A.
B.
C.
D.
5.如图,在△ABC中,点D在BC上,BD:DC=1:2,点E在AB上,AE:EB=3:2,AD,CE相交于F,则AF:FD=( )
A.3:1
B.3:2
C.4:3
D.9:4
6.如图,点D是BC边上一点且BD:DC=1:2,点F为线段AD上一点且AF:DF=1:2,BF的延长线交AC于E,则AE:AC=( )
A.1:2
B.1:3
C.1:4
D.1:7
7.如图.△ABC中,CD:DB=3:1,AE:EB=3:2,则CF:FE=( )
A.3
B.4
C.3:2
D.5
8.如图,在Rt△ABC中,∠C=90°,AC=BC=6cm,点P从点A出发,沿AB方向以每秒cm的速度向终点B运动;同时,动点Q从点B出发沿BC方向以每秒1cm的速度向终点C运动,将△PQC沿BC翻折,点P的对应点为点P′.设点Q运动的时间为t秒,若四边形QPCP′为菱形,则t的值为( )
A.
B.2
C.
D.3
9.如图,l1∥l2∥l3,则下列等式错误的是( )
A.
B.
C.
D.
二、填空题
10.如图,直线l1∥l2,AF:FB=2:3,BC:CD=2:1,则AE:EC是
.
11.如图,AD为△ABC的中线,AE=AD,BE交AC于点F,DH∥BF,则=
.
12.如图,在Rt△ABC中,∠ACB=90°,AB=4,点D,E分别在边AB,AC上,且DB=2AD,AE=3EC,连接BE,CD,相交于点O,则△ABO面积最大值为
.
13.如图,直线l1∥l2∥l3,等腰Rt△ABC的三个顶点A、B、C分别在直线l1、l2、l3上,∠ACB=90°,AC交l2于点D.若l1与l2的距离为1,l1与l3的距离为4,则的值是
.
14.如图,AD∥BE∥CF,直线l1,l2与这三条平行线分别交于点A,B,C和点D,E,F,=,DE=6,则EF=
.
三、解答题
15.如图,DE∥BC,EF∥CG,AD:AB=1:3,AE=3.
(1)求EC的值;
(2)求证:AD AG=AF AB.
16.已知如图,E为平行四边形ABCD的边AB的延长线上的一点,DE分别交AC、BC于G、F,试说明:DG是GE、GF的比例中项.
17.如图,DE∥BC,DF∥AC,AD=4cm,BD=8cm,DE=5cm,求线段BF的长.
18.在△ABC中,AD是高,E是AD的中点,连接CE,并延长交AB于点P,过点A作AQ∥BC,交CP的延长线于点Q,BD:CD:AD=1:2:3.
(1)求的值;
(2)若BD=5,求CQ的长.
19.如图,△ABC中,∠ACB=90°,AC=5,BC=12,CO⊥AB于点O,D是线段OB上一点,DE=2,ED∥AC(∠ADE<90°),连接BE、CD.BE、CD的中点分别为P、Q.
(1)求AO的长;
(2)求PQ的长;
(3)设PQ与AB的交点为M,请直接写出|PM﹣MQ|的值.
20.如图:已知Rt△ABC中∠C=90°,AC=3,BC=4,点E在AC上,E与A、C均不重合.
(1)若点F在AB上,且EF平分△ABC的周长,设AE=x,用含x的代数式表示S△AEF;
(2)若点F在折线ABC上移动,是否存在直线EF将Rt△ABC的周长与面积同时平分?若存在,求出AE的长,若不存在,请说出理由.
参考答案
1.解:过D点作DH∥BE交AC于H,如图,
∵F点为AD的中点,
∴AF=FD,
∵FE∥DH,
∴==1,即AE=EH,
∵DH∥BE,
∴==,CH=3EH,
∴=.
故选:A.
2.解:∵直线a∥b∥c,AC=4,CE=6,BD=3,
∴=,即=,解得DF=4.5.
故选:B.
3.解:∵DE∥BC,
∴==,
故选:C.
4.解:∵l1∥l2∥l3,
∴=,A错误;
=,B错误;
≠,C错误;
=,D正确.
故选:D.
5.解:过点D作DH∥CE交AB于H,
则==,
∵=,
∴=,
∵DH∥CE,
∴==,
∴AF:FD=9:4,
故选:D.
6.解:如图,过A作BC的平行线,交BE的延长线于G,
∵AG∥BD,
∴△AFG∽△DFB,
∴==,
即2AG=BD,
又∵BD:DC=1:2,
∴CD=2BD=4AG,
∴BC=6AG,
∵AG∥BC,
∴△AEG∽△CEB,
∴==,
∴CE=6AE,
∴=,
故选:D.
7.解:过点D作DK∥AB交CE于K,
∵CD:DB=3:1,AE:EB=3:2,
∴CK:KE=CD:DB=3:1,DK:BE=3:4,
∵AE:EB=3:2,
∴DK:AE=1:2,
∴KF:EF=DK:AE=1:2,
∴CF:EF=5.
故选:D.
8.解:连接PP′交BC于O,
∵若四边形QPCP′为菱形,
∴PP′⊥QC,
∴∠POQ=90°,
∵∠ACB=90°,
∴PO∥AC,
∴=,
∵设点Q运动的时间为t秒,
∴AP=t,QB=t,
∴QC=6﹣t,
∴CO=3﹣,
∵AC=CB=6,∠ACB=90°,
∴AB=6,
∴=,
解得:t=2,
故选:B.
9.解:∵l1∥l2∥l3,
∴,,,,
∴A、B、C都正确,D错误.
故选:D.
10.解:∵直线l1∥l2,
∴=,,
∵BC:CD=2:1,
∴=2,
∴AE:EC=2:1.
故答案为:2:1.
11.解:∵DH∥BF,AD为△ABC的中线,
∴CH=FH,
∵DH∥BF,AE=AD,
∴AF=FH,
∴=,
故答案为:.
12.解:如图,过点D作DF∥AE,
则==,
∵=,
∴DF=2EC,
∴DO=2OC,
∴DO=DC,
∴S△ADO=S△ADC,S△BDO=S△BDC,
∴S△ABO=S△ABC,
∵∠ACB=90°,
∴C在以AB为直径的圆上,设圆心为G,
当CG⊥AB时,△ABC的面积最大为:4×2=4,
此时△ABO的面积最大为:×4=.
故答案为:.
13.解:作AE⊥l3于E,交l2于F,作BH⊥l3于H,如图,
∵l1∥l2∥l3,
∴AF⊥l2,
∴EF=BH=3,AF=1,
∵△ABC为等腰直角三角形,
∴AC=BC,
∵∠ACB=90°,
∴∠ACE+∠CAE=90°,
∴∠ACE+∠BCH=90°,
∴∠CAE=∠BCH,
在△ACE和△CBH中,
,
∴△ACE≌△CBH(AAS),
∴CE=BH=3,
在Rt△ACE中,AC==5,
∴AB=AC=5,
∵DF∥CE,
∴==,
∴CD=,
在Rt△BCD中,BD==,
∴==.
故答案为.
14.解:∵AD∥BE∥CF,
∴=,即=,
∴EF=9.
故答案为9.
15.(1)解:
∵DE∥BC,
∴=,
又=,AE=3,
∴=,
解得AC=9,
∴EC=AC﹣AE=9﹣3=6;
(2)证明:
∵DE∥BC,EF∥CG,
∴==,
∴AD AG=AF AB.
16.解:∵四边形ABCD是平行四边形,
∴DC∥AE,
∴=,
∵AD∥BC,
∴=,
∴=,
∴DG2=GE GF,
∴DG是GE、GF的比例中项.
17.解:∵DE∥BC,DF∥AC,
∴四边形DECF是平行四边形,
∴FC=DE=5
cm.
∵DF∥AC,
∴
即
∴BF=10(cm).
18.解:(1)设BD=x,则CD=2x,AD=3x,BC=BD+CD=3x,
∵AQ∥BC,
∴==1,
∴AQ=CD=2x,
∴==;
(2)∵BD=5,BD:CD:AD=1:2:3,
∴CD=10,AD=15,
∵E是AD的中点,
∴DE=AD=7.5,
由勾股定理得,CE==,
∴CQ=25.
19.解:(1)如图1中,
∵CO⊥AB,
∴∠AOC=∠ACB=90°,∵∠A=∠A,
∴△ABC∽△ACO,
∴=,
∵AB===13,
∴OA==.
(2)如图2中,取BD中点F,CD中点Q,连接PF、QF,
则PF∥ED,FQ∥BC,PF⊥FQ,且PF=ED=1,FQ=BC=6,
在Rt△PFQ中,PQ===.
(3)如图3中,取AD中点G,连接GQ,
∵GQ∥AC,ED∥AC,PF∥ED,
∴PF∥GQ,
∴△PMF∽△QMG,
∴==,
∵PM+QM=,
∴PM=,MQ=,
∴|PM﹣QM|=.
20.解:(1)过点F作FM⊥AC于M,
EF平分△ABC的周长,AE=x,所以可得AE+AF=CE+BC+BF,
即:x+AF=3﹣x+4+5﹣AF,解得AF=6﹣x.
由平行线分线段成比例定理可知,
AF:AB=FM:BC,即,6﹣x:5=FM:4,
解得FM=,
所以S△AEF==
(2)若EF存在,
①当F在AB上时,如图1,
则由(1)可知,S△AEF==×=3,
化简得,2x2﹣12x+15=0,由△=122﹣4×2×15=24>0,
解得x1=,x2=(不合题意舍去).
即AE=.
②当F在BC上时,如图2,
CF+CE=AE+AB+BF,
即CF+3﹣x=x+5+4﹣CF,
CF=3+x,
根据面积平分得出S△CFE=S四边形BFEA=S△ACB=3,
即×(3﹣x)×(3+x)=3,
解得:x3=(舍弃),x4=﹣(舍去),
即存在直线EF将Rt△ABC的周长与面积同时平分,AE的长是
