2021-2022学年鲁教版九年级数学上册《2.6利用三角函数测高》优生辅导训练(word版含答案)
文档属性
| 名称 | 2021-2022学年鲁教版九年级数学上册《2.6利用三角函数测高》优生辅导训练(word版含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 645.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-06 00:00:00 | ||
图片预览


文档简介
2021-2022学年鲁教版九年级数学上册《2.6利用三角函数测高》优生辅导训练(附答案)
1.如图,某货船以20海里/小时的速度将一批重要物资由A处运往正西方向的目的地B处,经16小时的航行到达,到达后必须立即卸货,接到气象部门的通知,一台风中心正以40海里/小时的速度由A向北偏西60°方向移动,距台风中心200海里的圆形区域(包括边界)都会受到影响.
(1)B处是否会受到台风的影响,答:
(请填“会”或“不会”);
(2)为避免受到台风的影响,该船应在
小时内卸完货物.(结果保留根号)
2.某数学社团开展实践性研究,在大明湖南门A测得历下亭C在北偏东37°方向,继续向北走70m后到达游船码头B,测得历下亭C在游船码头B的北偏东53°方向.请计算一下南门A与历下亭C之间的距离约为
m.(参考数据:tan37°≈,tan53°≈)
3.如图,某海岸边有B,C两个码头,C码头位于B码头的正东方向,距离B码头60海里.甲、乙两船同时从A岛出发,甲船向位于A岛正北方向的B码头航行,乙船向位于A岛北偏东30°方向的C码头航行,当甲船到达距离B码头45海里的E处时,乙船位于甲船北偏东60°方向的D处,求此时乙船与C码头之间的距离.(结果保留根号)
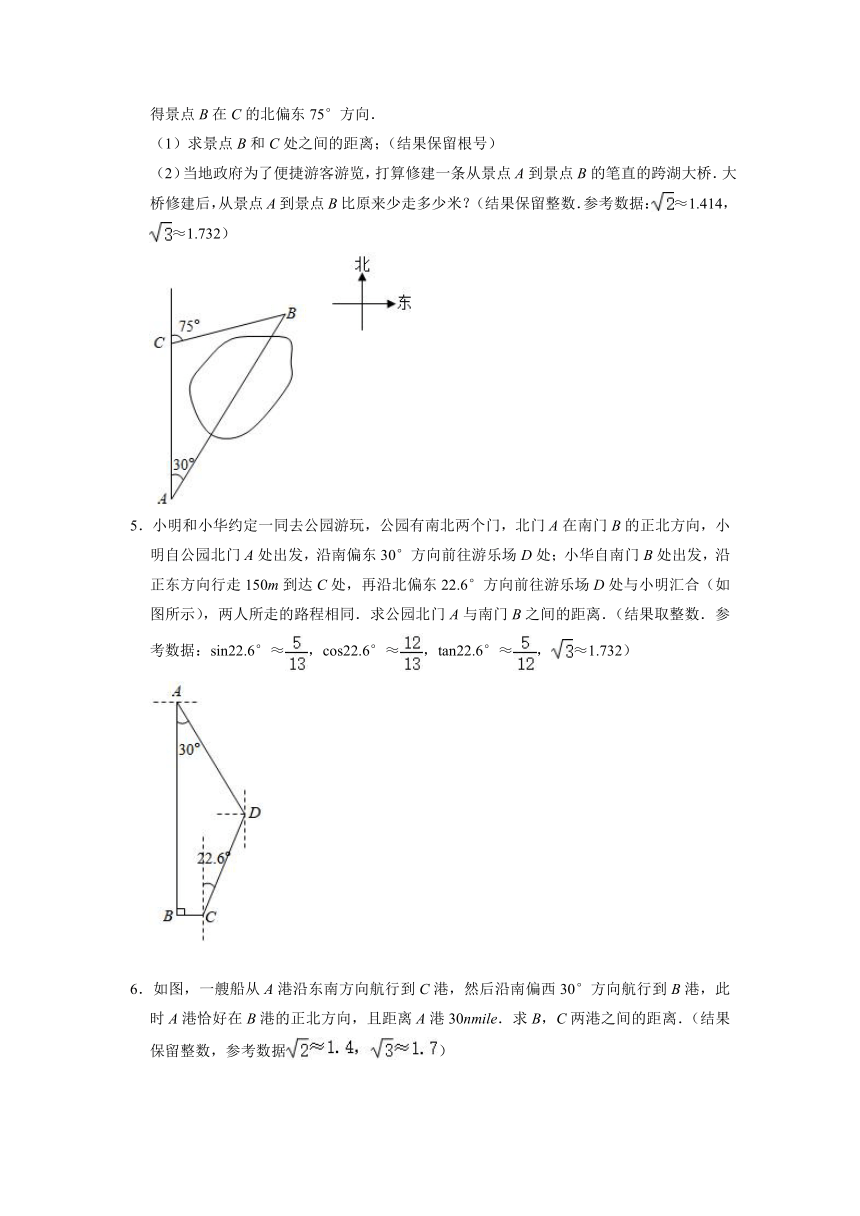
4.某景区A、B两个景点位于湖泊两侧,游客从景点A到景点B必须经过C处才能到达.观测得景点B在景点A的北偏东30°,从景点A出发向正北方向步行600米到达C处,测得景点B在C的北偏东75°方向.
(1)求景点B和C处之间的距离;(结果保留根号)
(2)当地政府为了便捷游客游览,打算修建一条从景点A到景点B的笔直的跨湖大桥.大桥修建后,从景点A到景点B比原来少走多少米?(结果保留整数.参考数据:≈1.414,≈1.732)
5.小明和小华约定一同去公园游玩,公园有南北两个门,北门A在南门B的正北方向,小明自公园北门A处出发,沿南偏东30°方向前往游乐场D处;小华自南门B处出发,沿正东方向行走150m到达C处,再沿北偏东22.6°方向前往游乐场D处与小明汇合(如图所示),两人所走的路程相同.求公园北门A与南门B之间的距离.(结果取整数.参考数据:sin22.6°≈,cos22.6°≈,tan22.6°≈,≈1.732)
6.如图,一艘船从A港沿东南方向航行到C港,然后沿南偏西30°方向航行到B港,此时A港恰好在B港的正北方向,且距离A港30nmile.求B,C两港之间的距离.(结果保留整数,参考数据)
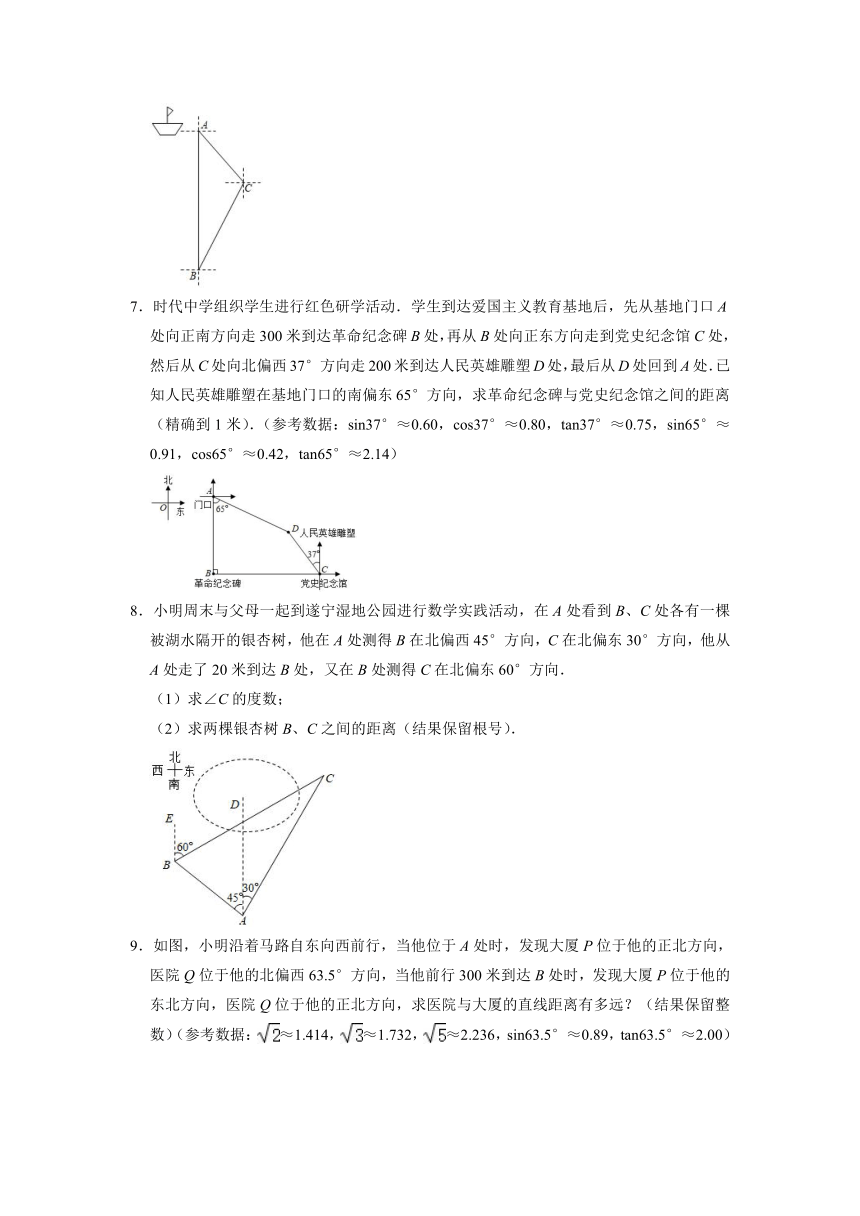
7.时代中学组织学生进行红色研学活动.学生到达爱国主义教育基地后,先从基地门口A处向正南方向走300米到达革命纪念碑B处,再从B处向正东方向走到党史纪念馆C处,然后从C处向北偏西37°方向走200米到达人民英雄雕塑D处,最后从D处回到A处.已知人民英雄雕塑在基地门口的南偏东65°方向,求革命纪念碑与党史纪念馆之间的距离(精确到1米).(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,sin65°≈0.91,cos65°≈0.42,tan65°≈2.14)
8.小明周末与父母一起到遂宁湿地公园进行数学实践活动,在A处看到B、C处各有一棵被湖水隔开的银杏树,他在A处测得B在北偏西45°方向,C在北偏东30°方向,他从A处走了20米到达B处,又在B处测得C在北偏东60°方向.
(1)求∠C的度数;
(2)求两棵银杏树B、C之间的距离(结果保留根号).
9.如图,小明沿着马路自东向西前行,当他位于A处时,发现大厦P位于他的正北方向,医院Q位于他的北偏西63.5°方向,当他前行300米到达B处时,发现大厦P位于他的东北方向,医院Q位于他的正北方向,求医院与大厦的直线距离有多远?(结果保留整数)(参考数据:≈1.414,≈1.732,≈2.236,sin63.5°≈0.89,tan63.5°≈2.00)
10.2021年5月7日,“雪龙2”船返回上海国内基地码头,标志着中国第37次南极考察圆满完成.已知“雪龙2”船上午9时在B市的南偏东25°方向上的点A处,且在C岛的北偏东59°方向上,已知B市在C岛的北偏东28°方向上,且距离C岛232km.此时,“雪龙2”船沿着AC方向以24km/h的速度航行.请你计算“雪龙2”船大约几点钟到达C岛?(数据:sin31°≈,cos31°≈,tan31°≈,sin53°≈,cos53°≈,tan53°≈)
11.如图,一艘轮船原计划从A地沿正东方向直接航行到B地,AB两地间的距离为200km.后来了解到在两地之间的某一海域有暗礁,为了避开暗礁,轮船从A地出发后就沿北偏东60°角的方向航行,到达C地后再沿南偏东45°角的方向继续航行到B地.请问轮船这样航行的路程比原计划的路程远了多少?(结果精确到1km;参考数据:≈1.41,≈1.73)
12.如图,小岛C和D都在码头O的正北方向上,它们之间距离为6.4km,一艘渔船自西向东匀速航行,行驶到位于码头O的正西方向A处时,测得∠CAO=26.5°,渔船速度为28km/h,经过0.2h,渔船行驶到了B处,测得∠DBO=49°.
(1)直接写出:在小岛C看点A俯角大小是
;点B在小岛D什么方位?
;
(2)求渔船在B处时距离码头O有多远?(结果精确到0.1km)
(参考数据:sin26.5°≈0.45,cos26.5°≈0.89,tan26.5°≈0.50,sin49°≈0.75,cos49≈0.66,tan49°≈1.15)
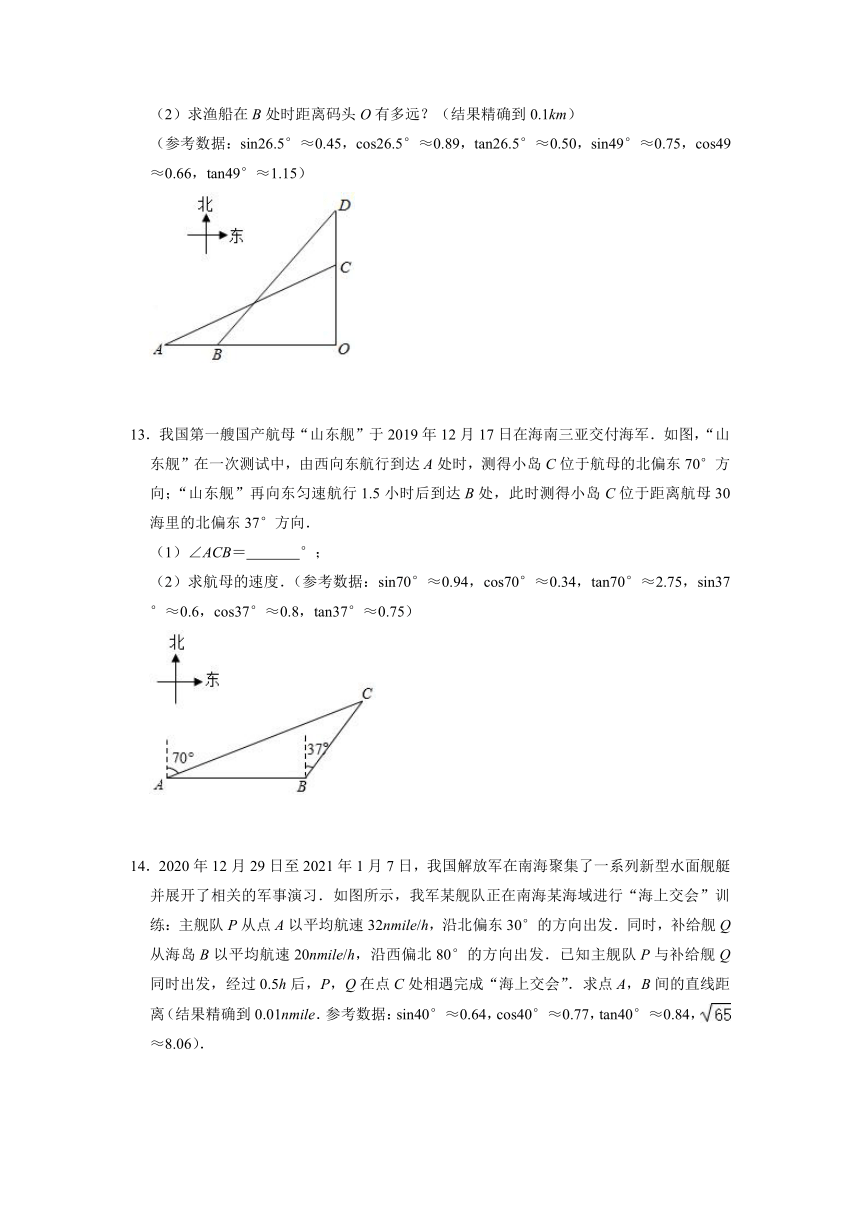
13.我国第一艘国产航母“山东舰”于2019年12月17日在海南三亚交付海军.如图,“山东舰”在一次测试中,由西向东航行到达A处时,测得小岛C位于航母的北偏东70°方向;“山东舰”再向东匀速航行1.5小时后到达B处,此时测得小岛C位于距离航母30海里的北偏东37°方向.
(1)∠ACB=
°;
(2)求航母的速度.(参考数据:sin70°≈0.94,cos70°≈0.34,tan70°≈2.75,sin37°≈0.6,cos37°≈0.8,tan37°≈0.75)
14.2020年12月29日至2021年1月7日,我国解放军在南海聚集了一系列新型水面舰艇并展开了相关的军事演习.如图所示,我军某舰队正在南海某海域进行“海上交会”训练:主舰队P从点A以平均航速32nmile/h,沿北偏东30°的方向出发.同时,补给舰Q从海岛B以平均航速20nmile/h,沿西偏北80°的方向出发.已知主舰队P与补给舰Q同时出发,经过0.5h后,P,Q在点C处相遇完成“海上交会”.求点A,B间的直线距离(结果精确到0.01nmile.参考数据:sin40°≈0.64,cos40°≈0.77,tan40°≈0.84,≈8.06).
15.如图,小李家在学校O的北偏东60°方向,距离学校8km的A处,小华家在学校O的东南方向的B处,小华家在小李家的正南方向,求小华家到学校的距离OB.
16.一辆汽车在A处测得东北方向(北偏东45°)有一古建筑C,汽车向正东方向以每小时40公里的速度行驶1小时到达B处时,又观测到古建筑C在北偏东16°方向上,求此时汽车与古建筑相距多少公里?(sin45°=0.71,sin61°≈0.87,cos61°≈0.48,tan61°≈1.80)
17.如图,C地在A地的正东方向,由于大山的阻隔,从A地到C地需要绕行B地、已知B地位于C地的南偏西60方向,B地距离C地200千米,A地位于B地的北偏西45°方向.现准备打通A、C两地的穿山隧道,修建A、C两地的直达高速公路.求A地到C地之间高速公路AC的长(结果保留根号).
18.某区域平面示意图如图所示,点D在河的右侧,人民路AB与桥BC垂直.某校数学小组进行研学活动时,在C处测得点D位于西北方向,又在A处测得点D位于南偏东65°方向,另测得BC=628m,AB=400m,求出点D到AB的距离.(结果保留整数,参考数据:sin65°≈0.91,cos65°≈0.42,tan65°≈2.14)
19.如图,小雪坐着轮船由点A出发沿正东方向AN航行,在点A处望湖中小岛M,测得小岛M在点A的北偏东60°,航行100米到达点B时,此时测得小岛M在点B的北偏东30°,求小岛M到航线AN的距离.
20.如图,甲乙两船同时从A港出发,甲船沿北偏东35°的方向,以每小时10海里的速度向B岛驶去.乙船沿南偏东55°的方向向C岛驶去,2小时后,两船同时到达了目的地.若C、B两岛的距离为海里,问乙船的航速是多少?
21.如图,小明同学在点P处测得教学楼A位于北偏东60°方向,办公楼B位于南偏东45°方向.小明沿正东方向前进60米到达C处,此时测得教学楼A恰好位于正北方向.办公楼B正好位于正南方向.求教学楼A与办公楼B之间的距离.(结果保留根号)
22.如图,为推进市中心城区污水系统综合治理项目,需要从A,B两地向C地新建AC,BC两条笔直的污水收集管道,现测得C地在A地北偏东45°方向上,在B地北偏西68°方向上,AB的距离为7km,求新建管道的总长度.(结果精确到0.1km)
参考数据sin22°≈0.37,cos22°≈0.93,tan22°≈0.40,≈1.41
23.如图,在某海域一艘巡逻舰由东向西匀速航行,速度为30nmile/h,该巡逻舰上午10:00在A处发现北偏西53°方向的C处船甲正在由南向北匀速航行,198s后,巡逻舰航行到B处,发现船甲在其北偏西45°方向且距其15nmile的D处.请你根据相关数据,求船甲的速度.(结果精确到1nmile/h.参考数据:sin53°≈,tan53°≈,cos53°≈)
24.某路段规定:汽车的最高行驶速度不得超过40km/h.如图,一辆汽车在该段道路上由西向东行驶,距离路边9m处有一车速检测仪O,测得该车从北偏西45°的A点行驶到北偏东53°的B点(点O,A,B在同一水平面内)所用时间为1.5s.试求该车从A点到B点的平均速度,并说明该车是否超速.(参考数据:sin53°≈,cos53°≈,tan53°≈)
25.纸上得来终觉浅,绝知此事要躬行.如图是某校的简化平面示意图,小明和小宁两位同学想要测算旗杆底部A处与公寓楼底部C处之间的距离,但当小明站在旗杆底部A处、小宁站在公寓楼的底部C处时,发现由于办公楼的遮挡无法测量相关数据,于是小宁来到公寓楼的底部B处,发现能够看到小明,并利用自制测角仪测得A处在B处的南偏西53°方向上,即∠ABS=53°.已知旗杆底部A处与公寓楼底部B处之间的距离为250m.公寓楼东西长BC=50m.试求旗杆底部A处与公寓楼底部C处之间的距离(结果精确到1m.参考数据:sin53°≈,cos53°≈,tan53°≈,≈1.414)
26.2020年11月10日,“雪龙2”起航!中国第37次南极考察队从上海出发,执行南极考察任务.已知“雪龙2”船上午9时在B市的南偏东25°方向上的点A处,且在C岛的北偏东58°方向上,已知B市在C岛的北偏东28°方向上,且距离C岛248km.此时,“雪龙2”船沿着AC方向以25km/h的速度运动.请你计算“雪龙2”船大约几点钟到达C岛?(结果精确到1km.参考数据:≈1.73,sin53°≈,cos53°≈,tan53°≈)
27.如图,小岛A在港口P的南偏西37°方向,距离港口81海里处.甲船从A出发,沿AP方向以9海里/时的速度驶向港口,乙船从港口P出发,沿南偏东60°方向,以18海里/时的速度驶离港口,现两船同时出发.
(1)出发后几小时两船与港口P的距离相等?
(2)出发后几小时乙船在甲船的正东方向?(sin37°≈,cos37°≈,tan37°≈)
28.一艘海监船从A点沿正北方向巡航,其航线距某岛屿(设N、M为该岛屿的东西两端点)最近距离为15海里(即MC=15海里),在A点测得岛屿的西端点M在点A的东北方向,航行4海里后到达B点,测得岛屿的东端点N在点B的北偏东62°方向(其中N、M、C在同一条直线上),求该岛屿东西两端点MN之间的距离.(精确到0.1海里)(参考数据:sin62°≈0.88,cos62°≈0.47,tan62°≈1.87)
29.如图,一艘轮船原计划从A地直接航行到B地,两地间的距离AB为200km.后来了解到在两地之间的某一海域有暗礁,为了避开暗礁,轮船从A地出发后,就沿与水平线成30°角的方向航行,到达C地后再沿与水平线成45°角的方向继续航行直到B地.请问轮船这样航行的路程比原计划的路程远了多少?(要求在结果化简后再代入参考数据运算,最终结果精确到1km;参考数据:≈1.73,≈1.41).
30.如图,某渔船在完成捕捞作业后准备返回港口C,途经某海域A处时,港口C的工作人员监测到点A在南偏东30°方向上,另一港口B的工作人员监测到点A在正西方向上.已知港口C在港口B的北偏西60°方向,且B、C两地相距120海里.
(1)求出此时点A到港口C的距离(计算结果保留根号);
(2)若该渔船从A处沿AC方向向港口C驶去,当到达点A'时,测得港口B在A'的南偏东75°的方向上,求此时渔船的航行距离(计算结果保留根号).
参考答案
1.解:(1)由题意可知,AB=20×16=320海里,∠BAC=90°﹣60°,
过点B作BM⊥AC,垂足为M,
在Rt△ABM中,AB=320海里,∠BAM=30°,
∴BM=×320=160(海里)<200海里,
AM=×320=160海里,
∴B处会受到台风的影响,
故答案为:会;
(2)设台风初次影响B处时,此时台风中心为N,则BN=200海里,如图,
在Rt△BMN中,BN=200海里,BM=160海里,
∴MN===120(海里),
∴AN=AM﹣MN=(160﹣120)海里,
因此需要的时间为:=(8﹣6)小时,
故答案为:8﹣6.
2.解:如图,过C作CE⊥BA于E.
设EC=xm,BE=ym,
在Rt△ECB中,tan53°=≈,
即≈①,
在Rt△AEC中,tan37°=≈,
即≈②,
由①②得:x=120,y=90,
∴EC=120m,BE=90m,
∴AE=70+90=160(m),
∴AC===200(m),
故答案为:200.
3.解:如图,分别延长BC,ED交于F,
由题意得,∠B=90°,∠A=30°,∠BED=60°,
∴∠ADE=∠BED﹣∠A=30°,∠F=90°﹣∠BED=30°,
∵∠CDF=∠ADE=30°,
∴∠CDF=∠F,
∴CD=CF,
在Rt△BEF中,∠BED=60°,BE=45海里,
∴BF=BE tan60°=45(海里),
∴CF=BF﹣BC=(45﹣60)(海里),
∴CD=(45﹣60)海里,
答:此时乙船与C码头之间的距离为(45﹣60)海里.
4.解:(1)过点C作CD⊥AB于点D,
由题意得,∠A=30°,∠BCE=75°,AC=600m,
在Rt△ACD中,∠A=30°,AC=600,
∴CD=AC=300(m),
AD=AC=300(m),
∵∠BCE=75°=∠A+∠B,
∴∠B=75°﹣∠A=45°,
∴CD=BD=300(m),
BC=CD=300(m),
答:景点B和C处之间的距离为300m;
(2)由题意得.
AC+BC=(600+300)m,
AB=AD+BD=(300+300)m,
AC+BC﹣AB=(600+300)﹣(300+300)
≈204.6
≈205(m),
答:大桥修建后,从景点A到景点B比原来少走约205m.
5.解:作DE⊥AB于E,CF⊥DE于F,
∵BC⊥AB,
∴四边形BCFE是矩形,
∴BE=CF,EF=BC=150
m,
设DF=xm,则DE=(x+150)m,
在Rt△ADE中,∠BAD=30°,
∴AD=2DE=2(x+150)m,
在Rt△DCF中,∠FCD=22.6°,
∴CD=≈=xm,
∵AD=CD+BC,
∴2(x+150)=+150,
解得x=250(m),
∴DF=250
m,
∴DE=250+150=400
m,
∴AD=2DE=800
m,
∴CD=800﹣150=650
m,
由勾股定理得AE===400
m,
BE=CF===600
m,
∴AB=AE+BE=400+600≈1293(m),
答:公园北门A与南门B之间的距离约为1293
m.
6.解:如图,过点C作CH⊥AB于H.
∵∠AHC=90°,∠CAH=45°,
∴∠ACH=∠CAH=45°,
∴AH=CH,
设AH=CH=xnmile,
在Rt△CBH中,∠CHB=90°,∠CBH=30°,
∴BC=2CH=2x(nmile),BH=CH=x(nmile),
∵AB=AH+BH=30nmile,
∴x+x=30,
∴x=15(﹣1),
∴BC=2x=30(﹣1)≈21(nmile).
7.解:过D作DE⊥AB于E,DF⊥BC于F,如图所示:
由题意得:∠CDF=37°,CD=200米,
在Rt△CDF中,sin∠CDF==sin37°≈0.60,cos∠CDF==cos37°≈0.80,
∴CF≈200×0.60=120(米),DF≈200×0.80=160(米),
∵AB⊥BC,DF⊥BC,DE⊥AB,
∴∠B=∠DFB=∠DEB=90°,
∴四边形BFDE是矩形,
∴BF=DE,BE=DF=160米,
∴AE=AB﹣BE=300﹣160=140(米),
在Rt△ADE中,tan∠DAE==tan65°≈2.14,
∴DE≈AE×2.14=140×2.14=299.60(米),
∴BF=DE≈299.60(米),
∴BC=BF+CF=299.60+120≈420(米),
答:革命纪念碑与党史纪念馆之间的距离约为420米.
8.解:(1)设AD与BC交于点F,
由题意得BE∥AD,
∵BE∥AD且∠EBF=60°,
∴∠BFA=∠EBF=60°,
∵∠BFA=∠C+∠CAD且∠CAD=30°,
∴∠C=∠BFA﹣∠CAD=30°;
(2)过点B作BG⊥AD于G.
∵BG⊥AD,
∴∠AGB=∠BGD=90°,
在Rt△AGB中,AB=20米,∠BAG=45°,
AG=BG=20×sin45°=(米),
在Rt△BGF中,∠BFG=60°,
∴BF===(米),FG=BGtan60°===(米),
∵∠C=∠CAD=30°,
∴CF=AF=AG+FG=(10+)(米),
∴BC=BF+CF=(10+10)米,
答:两棵银杏树B、C之间的距离为(10+10)米.
9.解:如图,过Q作QC⊥AP于C,
由题意知,QB⊥AB,PA⊥AB,∠PAQ=63.5°,∠ABP=45°,AB=300米,
∴∠BAP=∠ABQ=90°,
∴AP∥BQ,
∴四边形ACQB是矩形,
∴∠AQB=∠PAQ=63.5°,AC=BQ,CQ=AB=300(米),
在Rt△ABP中,∠ABP=45°,
∴PA=AB=300米,
在Rt△ABQ中,tan63.5°=,
∴BQ≈=150(米),
∴PC=150米,
∴PQ==150≈335(米),
故医院与大厦的直线距离有335米.
10.解:过点A作AD⊥BC于D,
由题意知,∠ABC=28°+25°=53°,∠ACB=59°﹣28°=31°,BC=232km,
设AD=x,
在Rt△ABD中,∵∠ABD=53°,
∴BD==≈x,
在Rt△ACD中,∵∠ACD=30°,
∴CD===x,
∵BD+CD=BC,
∴x+x=232,
解得:x=96,
∴AD=96(km),
∴AC=2AD=192(km),
∴192÷24=8(h),
∴9+8=17,
答:“雪龙2”船大约17点钟到达C岛.
11.解:过点C作CD⊥AB于点D,如图所示:
则∠CAD=90°﹣60°=30°,∠CBD=45°,AD==CD,BD==CD,
∵AD+BD=AB,
∴(+1)CD=200km,
∴CD=100(﹣1)km,
在Rt△ACD中,AC=200(﹣1)km,
在Rt△BCD中,BC=100(﹣1),
AC+BC=200(﹣1)+100(﹣1)≈249(km),
249﹣200=49(km),
答:飞机的飞行路程比原来的路程远了约49km.
12.解:(1)过C作CE∥OA,如图所示:
则∠ACE=∠CAO=26.5°,
即在小岛C看点A俯角大小是26.5°,
由题意得:∠DOB=90°,
∵∠DBO=49°,
∴∠BDO=90°﹣49°=41°,
∴点B在小岛D南偏西41°方向上,
故答案为:26.5°,南偏西41°;
(2)设B处距离码头O有xkm,
由题意得:AB=28×0.2=5.6(km),
则OA=AB+BO=(5.6+x)km,
在Rt△CAO中,∠CAO=26.5°,
∵tan∠CAO=,
∴OC=OA tan∠CAO=(5.6+x) tan26.5°≈(5.6+x)×0.50=(2.8+0.5x)km,
在Rt△DBO中,∠DBO=49°,
∵tan∠DBO=,
∴DO=BO tan∠DBO=x tan49°≈1.15x(km),
∵DC=DO﹣CO,
∴6.4=1.15x﹣(2.8+0.5x),
解得:x≈14.2(km).
答:B处距离码头O约14.2km.
13.解:(1)过点C作CD⊥AB交AB的延长线于D.
由题意可知,∠ACD=70°,∠BCD=37°,
∴∠ACB=∠ACD﹣∠BCD=33°,
故答案为33;
(2)如图,在Rt△BCD中,BC=30,∠BCD=37°,
∴BD=BC sin∠BCD≈18(海里),CD=BC cos∠BCD≈24(海里),
在Rt△ACD中,CD=24海里,∠ACD=70°,
∴AD=24 tan∠ACD≈66(海里),
∴航母的速度为(66﹣18)÷1.5=32(海里/时).
答:航母的速度为32海里/时.
14.解:如图,过点B作BD⊥AC,垂足为D,连接AB,
由题意得,AC=32×0.5=16(nmile),BC=20×0.5=10(nmile),∠α=30°,∠β=80°,
∴∠C=30°+(90°﹣80°)=40°,
在Rt△BCD中,
CD=BC cosC≈10×0.77=7.7(nmile),
BD=BC sinC≈10×0.64=6.4(nmile),
∴AD=AC﹣CD=16﹣7.7=8.3(nmile),
在Rt△ADB中,
AB==≈10.48(nmile),
答:点A,B间的直线距离约为10.48nmile.
15.解:过点O作OC⊥AB,垂足为C,则∠AOC=90°﹣60°=30°,
∠BOC=90°﹣45°=45°,
在Rt△AOC中,
OC=OA cos30°=8×=4(km),
在Rt△BOC中,
OB===4(km),
答:小华家到学校的距离OB为4km.
16.解:过B作BD⊥AC,垂足为D,过B作BE⊥AB,交AC于E.
Rt△ABD中,∠DAB=45°,AB=40×1=40(公里),
∴BD=ABsin45°=40×=20(公里),
Rt△CBD中,∠CBD=∠CBE+∠EBD=45°+16°=61°,
∴BC=≈=(公里),
答:此时汽车与古建筑相距公里.
17.解:如图,过点B作BD⊥AC于点D,
根据题意,得∠CBD=60°,CB=200,∠ABD=45°,
在Rt△CBD中,BD=CB cos60°=200×=100(千米),CD=CB sin60°=200×=100(千米),
在Rt△ABD中,AD=BD tan45°=100(千米),
∴(千米),
答:A地到C地之间高速公路AC长千米.
18.解:如图,过点D作DE⊥AB于E,过D作DF⊥BC于F,则四边形EBFD是矩形,
设DE=x,
在Rt△ADE中,∠AED=90°,
∵tan∠DAE=,
∴AE=≈,
∴BE=AB﹣AE=(400﹣)m,
又BF=DE=xm,
∴CF=BC﹣BF=(628﹣x)m,
在Rt△CDF中,∠DFC=90°,∠DCF=45°,
∴∠CDF=45°,
∴∠CDF=∠DCF,
∴DF=CF=(628﹣x)m.
又BE=DF,
即:400﹣=(628﹣x)m,
解得:x≈428.
答:点D到AB的距离约428m.
19.解:过M作MD⊥AN于D,如图所示:
由题意得:AB=100米,∠MAB=90°﹣60°=30°,∠MBD=90°﹣30°=60°,
∴∠AMB=∠MBD﹣∠MAB=30°,
∴∠MAB=∠AMB,
∴MB=AB=100(米),
在Rt△BDM中,∠BMD=90°﹣60°=30°,
∴BD=MB=50(米),
∴MD=BD=50(米),
答:小岛M到航线AN的距离为50米.
20.解:根据题意得:AB=10×2=20(海里),BC=海里,∠BAC=180°﹣35°﹣55°=90°,
∴AC2+AB2=BC2,
∴,
∴AC=30(海里),
∴乙船的航速为:30÷2=15(海里/时),
答:乙船的航速是15海里/时.
21.解:由题意可知:∠ACP=∠BCP=90°,∠APC=90°﹣60°=30°,∠BPC=45°.
在Rt△BPC中,∠BCP=90°,∠B=∠BPC=45°,
∴BC=PC=60米,
在Rt△ACP中,∠ACP=90°,∠APC=30°,
∵tan30°=,
∴AC=PC tan30°=tan30°×60=60×=20(米).
∴AB=AC+BC=(60+20)米,
答:教学楼A与办公楼B之间的距离是(60+20)米.
22.解:作CD⊥AB于点D,
由题意可得,
∠CAD=45°,∠CBD=90°﹣68°=22°,
设CD=x,
则AD=CD=x,BD=AB﹣AD=7﹣x,
∵tan∠CBD==,tan22°≈0.40,
∴0.40≈,
解得x=2,
∵AC=,BC=,
∴AC+BC≈+≈8.2(km),
答:新建管道的总长度是8.2km.
23.解:如图,延长AB、DC相交于点E,则∠E=90°,
在Rt△DEB中,∠D=∠DBE=45°,BD=15nmile,
∴DE=BE=BD sin45°=15(nmile),
198s=0.055h,
AB=30×0.055=1.65(nmile),
∴AE=AB+BE=1.65+15=16.65(nmile),
在Rt△ACE中,∠ACE=53°,
∴CE==≈12.4875(nmile),
∴CD=15﹣12.4875=2.5125(nmile),
∴甲船的速度为2.5125÷0.055=45.68≈46(nmile/h),
答:船甲的速度为46nmile/h.
24.解:如图,过O作OC⊥AB于点C,
由题意得:OC=9m,
在Rt△AOC中,∠AOC=45°,
∴∠OAC=45°,
∴AC=OC=9(m),
在Rt△BOC中,∠BOC=53°,
∴BC=OC tan∠BOC≈9×=12(m),
∴AB=AC+BC=9+12=21(m),
21÷1.5=14(m/s),
14m/s=50.4km/h>40km/h,
∴超速了.
25.解:如图,由题意知,AB=250m,BC=50m,
过点A作AE⊥BS,交BS的延长线于点E,过点C作CD⊥AE于点D,则四边形BCDE是矩形,
∴DE=BC=50(m),CD=BE,
在Rt△ABE中,AB=250m,∠ABE=53°,
∴BE=AB cos∠ABE≈250×=150(m),AE=AB sin∠ABE≈250×=200(m),
在Rt△ACD中,∠ADC=90°,AD=AE﹣DE=200﹣50=150(m),CD=BE=150(m),
∴AC=(m),
即旗杆底部A处与公寓楼底部C处之间的距离约为212米.
26.解:过点A作AD⊥BC于D,
由题意知,∠ABC=28°+25°=53°,∠ACB=58°﹣28°=30°,BC=248km,
设AD=x,
在Rt△ABD中,∵∠ABD=53°,
∴BD=,
在Rt△ACD中,∵∠ACD=30°,
∴CD=,
∵BD+CD=BC,
∴,
解得:x≈100,
∴AD=100(km),
∴AC=2AD=200(km),
∴200÷25=8(h),
∴9+8=17,
答:“雪龙2”船大约17点钟到达C岛.
27.解:(1)设出发后x小时两船与港口P的距离相等.
根据题意得81﹣9x=18x.
解得x=3.
故出发后3小时两船与港口P的距离相等.
(2)设出发后y小时乙船在甲船的正东方向,
此时甲、乙两船的位置分别在点C,D处.
连接CD,过点P作PE⊥CD,垂足为E.
则点E在点P的正南方向.
在Rt△CEP中,∠CPE=37°,
则PE=PC cos37°.
在Rt△PED中,∠EPD=60°,
则PE=PD cos60°.
则PC cos37°=PD cos60°.
则(81﹣9y)cos37°=18y cos60°.
,
解得y=4.
答:出发后4小时乙船在甲船的正东方向.
28.解:由题意可知:AB=4海里,∠CAM=45°,∠CBN=62°,∠ACN=90°.
在Rt△ACM中,
∵MC=15,∠CAM=45°,
∴(海里),
∵AB=4海里,
∴BC=AC﹣AB=15﹣4=11(海里),
在Rt△BCND中,
∵∠CBN=62°,
∴NC=BC tan∠CBN=11 tan62°≈11×1.87=20.57(海里),
∴MN=NC﹣MC=20.57﹣15=5.57≈5.6(海里),
答:该岛屿东西两端点MN之间的距离为5.6海里.
29.解:过点C作CD⊥AB于点D,则AD=,BD=,
∵AD+BD=AB,
∴(+1)CD=200,
∴CD=100(﹣1),
在Rt△ACD中,AC=200(﹣1),
在Rt△BCD中,BC=100(﹣1),
AC+BC=200(﹣1)+100(﹣1)≈250(km),
250﹣200=50(km),
答:轮船这样航行的路程比原计划的路程远了50km.
30.解:(1)如图所示:延长BA,过点C作CD⊥BA延长线于点D,
由题意可得:∠CBD=30°,BC=120海里,
则CD=BC=60海里,
∵cos∠ACD==cos30°=,
即=,
∴AC=40(海里),
答:此时点A到军港C的距离为40海里;
(2)过点A′作A′N⊥BC于点N,如图:
由(1)得:CD=60海里,AC=40海里,
∵A'E∥CD,
∴∠AA'E=∠ACD=30°,
∴∠BA′A=45°,
∵∠BA'E=75°,
∴∠ABA'=15°,
∴∠2=15°=∠ABA',
即A′B平分∠CBA,
∴A'E=A'N,
设AA′=x,则AE=AA',A'N=A′E=AE=x,
∵∠1=60°﹣30°=30°,A'N⊥BC,
∴A'C=2A'N=x,
∵A'C+AA'=AC,
∴x+x=40,
解得:x=60﹣20,
∴AA'=(60﹣20)海里,
答:此时渔船的航行距离为(60﹣20)海里.
1.如图,某货船以20海里/小时的速度将一批重要物资由A处运往正西方向的目的地B处,经16小时的航行到达,到达后必须立即卸货,接到气象部门的通知,一台风中心正以40海里/小时的速度由A向北偏西60°方向移动,距台风中心200海里的圆形区域(包括边界)都会受到影响.
(1)B处是否会受到台风的影响,答:
(请填“会”或“不会”);
(2)为避免受到台风的影响,该船应在
小时内卸完货物.(结果保留根号)
2.某数学社团开展实践性研究,在大明湖南门A测得历下亭C在北偏东37°方向,继续向北走70m后到达游船码头B,测得历下亭C在游船码头B的北偏东53°方向.请计算一下南门A与历下亭C之间的距离约为
m.(参考数据:tan37°≈,tan53°≈)
3.如图,某海岸边有B,C两个码头,C码头位于B码头的正东方向,距离B码头60海里.甲、乙两船同时从A岛出发,甲船向位于A岛正北方向的B码头航行,乙船向位于A岛北偏东30°方向的C码头航行,当甲船到达距离B码头45海里的E处时,乙船位于甲船北偏东60°方向的D处,求此时乙船与C码头之间的距离.(结果保留根号)
4.某景区A、B两个景点位于湖泊两侧,游客从景点A到景点B必须经过C处才能到达.观测得景点B在景点A的北偏东30°,从景点A出发向正北方向步行600米到达C处,测得景点B在C的北偏东75°方向.
(1)求景点B和C处之间的距离;(结果保留根号)
(2)当地政府为了便捷游客游览,打算修建一条从景点A到景点B的笔直的跨湖大桥.大桥修建后,从景点A到景点B比原来少走多少米?(结果保留整数.参考数据:≈1.414,≈1.732)
5.小明和小华约定一同去公园游玩,公园有南北两个门,北门A在南门B的正北方向,小明自公园北门A处出发,沿南偏东30°方向前往游乐场D处;小华自南门B处出发,沿正东方向行走150m到达C处,再沿北偏东22.6°方向前往游乐场D处与小明汇合(如图所示),两人所走的路程相同.求公园北门A与南门B之间的距离.(结果取整数.参考数据:sin22.6°≈,cos22.6°≈,tan22.6°≈,≈1.732)
6.如图,一艘船从A港沿东南方向航行到C港,然后沿南偏西30°方向航行到B港,此时A港恰好在B港的正北方向,且距离A港30nmile.求B,C两港之间的距离.(结果保留整数,参考数据)
7.时代中学组织学生进行红色研学活动.学生到达爱国主义教育基地后,先从基地门口A处向正南方向走300米到达革命纪念碑B处,再从B处向正东方向走到党史纪念馆C处,然后从C处向北偏西37°方向走200米到达人民英雄雕塑D处,最后从D处回到A处.已知人民英雄雕塑在基地门口的南偏东65°方向,求革命纪念碑与党史纪念馆之间的距离(精确到1米).(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,sin65°≈0.91,cos65°≈0.42,tan65°≈2.14)
8.小明周末与父母一起到遂宁湿地公园进行数学实践活动,在A处看到B、C处各有一棵被湖水隔开的银杏树,他在A处测得B在北偏西45°方向,C在北偏东30°方向,他从A处走了20米到达B处,又在B处测得C在北偏东60°方向.
(1)求∠C的度数;
(2)求两棵银杏树B、C之间的距离(结果保留根号).
9.如图,小明沿着马路自东向西前行,当他位于A处时,发现大厦P位于他的正北方向,医院Q位于他的北偏西63.5°方向,当他前行300米到达B处时,发现大厦P位于他的东北方向,医院Q位于他的正北方向,求医院与大厦的直线距离有多远?(结果保留整数)(参考数据:≈1.414,≈1.732,≈2.236,sin63.5°≈0.89,tan63.5°≈2.00)
10.2021年5月7日,“雪龙2”船返回上海国内基地码头,标志着中国第37次南极考察圆满完成.已知“雪龙2”船上午9时在B市的南偏东25°方向上的点A处,且在C岛的北偏东59°方向上,已知B市在C岛的北偏东28°方向上,且距离C岛232km.此时,“雪龙2”船沿着AC方向以24km/h的速度航行.请你计算“雪龙2”船大约几点钟到达C岛?(数据:sin31°≈,cos31°≈,tan31°≈,sin53°≈,cos53°≈,tan53°≈)
11.如图,一艘轮船原计划从A地沿正东方向直接航行到B地,AB两地间的距离为200km.后来了解到在两地之间的某一海域有暗礁,为了避开暗礁,轮船从A地出发后就沿北偏东60°角的方向航行,到达C地后再沿南偏东45°角的方向继续航行到B地.请问轮船这样航行的路程比原计划的路程远了多少?(结果精确到1km;参考数据:≈1.41,≈1.73)
12.如图,小岛C和D都在码头O的正北方向上,它们之间距离为6.4km,一艘渔船自西向东匀速航行,行驶到位于码头O的正西方向A处时,测得∠CAO=26.5°,渔船速度为28km/h,经过0.2h,渔船行驶到了B处,测得∠DBO=49°.
(1)直接写出:在小岛C看点A俯角大小是
;点B在小岛D什么方位?
;
(2)求渔船在B处时距离码头O有多远?(结果精确到0.1km)
(参考数据:sin26.5°≈0.45,cos26.5°≈0.89,tan26.5°≈0.50,sin49°≈0.75,cos49≈0.66,tan49°≈1.15)
13.我国第一艘国产航母“山东舰”于2019年12月17日在海南三亚交付海军.如图,“山东舰”在一次测试中,由西向东航行到达A处时,测得小岛C位于航母的北偏东70°方向;“山东舰”再向东匀速航行1.5小时后到达B处,此时测得小岛C位于距离航母30海里的北偏东37°方向.
(1)∠ACB=
°;
(2)求航母的速度.(参考数据:sin70°≈0.94,cos70°≈0.34,tan70°≈2.75,sin37°≈0.6,cos37°≈0.8,tan37°≈0.75)
14.2020年12月29日至2021年1月7日,我国解放军在南海聚集了一系列新型水面舰艇并展开了相关的军事演习.如图所示,我军某舰队正在南海某海域进行“海上交会”训练:主舰队P从点A以平均航速32nmile/h,沿北偏东30°的方向出发.同时,补给舰Q从海岛B以平均航速20nmile/h,沿西偏北80°的方向出发.已知主舰队P与补给舰Q同时出发,经过0.5h后,P,Q在点C处相遇完成“海上交会”.求点A,B间的直线距离(结果精确到0.01nmile.参考数据:sin40°≈0.64,cos40°≈0.77,tan40°≈0.84,≈8.06).
15.如图,小李家在学校O的北偏东60°方向,距离学校8km的A处,小华家在学校O的东南方向的B处,小华家在小李家的正南方向,求小华家到学校的距离OB.
16.一辆汽车在A处测得东北方向(北偏东45°)有一古建筑C,汽车向正东方向以每小时40公里的速度行驶1小时到达B处时,又观测到古建筑C在北偏东16°方向上,求此时汽车与古建筑相距多少公里?(sin45°=0.71,sin61°≈0.87,cos61°≈0.48,tan61°≈1.80)
17.如图,C地在A地的正东方向,由于大山的阻隔,从A地到C地需要绕行B地、已知B地位于C地的南偏西60方向,B地距离C地200千米,A地位于B地的北偏西45°方向.现准备打通A、C两地的穿山隧道,修建A、C两地的直达高速公路.求A地到C地之间高速公路AC的长(结果保留根号).
18.某区域平面示意图如图所示,点D在河的右侧,人民路AB与桥BC垂直.某校数学小组进行研学活动时,在C处测得点D位于西北方向,又在A处测得点D位于南偏东65°方向,另测得BC=628m,AB=400m,求出点D到AB的距离.(结果保留整数,参考数据:sin65°≈0.91,cos65°≈0.42,tan65°≈2.14)
19.如图,小雪坐着轮船由点A出发沿正东方向AN航行,在点A处望湖中小岛M,测得小岛M在点A的北偏东60°,航行100米到达点B时,此时测得小岛M在点B的北偏东30°,求小岛M到航线AN的距离.
20.如图,甲乙两船同时从A港出发,甲船沿北偏东35°的方向,以每小时10海里的速度向B岛驶去.乙船沿南偏东55°的方向向C岛驶去,2小时后,两船同时到达了目的地.若C、B两岛的距离为海里,问乙船的航速是多少?
21.如图,小明同学在点P处测得教学楼A位于北偏东60°方向,办公楼B位于南偏东45°方向.小明沿正东方向前进60米到达C处,此时测得教学楼A恰好位于正北方向.办公楼B正好位于正南方向.求教学楼A与办公楼B之间的距离.(结果保留根号)
22.如图,为推进市中心城区污水系统综合治理项目,需要从A,B两地向C地新建AC,BC两条笔直的污水收集管道,现测得C地在A地北偏东45°方向上,在B地北偏西68°方向上,AB的距离为7km,求新建管道的总长度.(结果精确到0.1km)
参考数据sin22°≈0.37,cos22°≈0.93,tan22°≈0.40,≈1.41
23.如图,在某海域一艘巡逻舰由东向西匀速航行,速度为30nmile/h,该巡逻舰上午10:00在A处发现北偏西53°方向的C处船甲正在由南向北匀速航行,198s后,巡逻舰航行到B处,发现船甲在其北偏西45°方向且距其15nmile的D处.请你根据相关数据,求船甲的速度.(结果精确到1nmile/h.参考数据:sin53°≈,tan53°≈,cos53°≈)
24.某路段规定:汽车的最高行驶速度不得超过40km/h.如图,一辆汽车在该段道路上由西向东行驶,距离路边9m处有一车速检测仪O,测得该车从北偏西45°的A点行驶到北偏东53°的B点(点O,A,B在同一水平面内)所用时间为1.5s.试求该车从A点到B点的平均速度,并说明该车是否超速.(参考数据:sin53°≈,cos53°≈,tan53°≈)
25.纸上得来终觉浅,绝知此事要躬行.如图是某校的简化平面示意图,小明和小宁两位同学想要测算旗杆底部A处与公寓楼底部C处之间的距离,但当小明站在旗杆底部A处、小宁站在公寓楼的底部C处时,发现由于办公楼的遮挡无法测量相关数据,于是小宁来到公寓楼的底部B处,发现能够看到小明,并利用自制测角仪测得A处在B处的南偏西53°方向上,即∠ABS=53°.已知旗杆底部A处与公寓楼底部B处之间的距离为250m.公寓楼东西长BC=50m.试求旗杆底部A处与公寓楼底部C处之间的距离(结果精确到1m.参考数据:sin53°≈,cos53°≈,tan53°≈,≈1.414)
26.2020年11月10日,“雪龙2”起航!中国第37次南极考察队从上海出发,执行南极考察任务.已知“雪龙2”船上午9时在B市的南偏东25°方向上的点A处,且在C岛的北偏东58°方向上,已知B市在C岛的北偏东28°方向上,且距离C岛248km.此时,“雪龙2”船沿着AC方向以25km/h的速度运动.请你计算“雪龙2”船大约几点钟到达C岛?(结果精确到1km.参考数据:≈1.73,sin53°≈,cos53°≈,tan53°≈)
27.如图,小岛A在港口P的南偏西37°方向,距离港口81海里处.甲船从A出发,沿AP方向以9海里/时的速度驶向港口,乙船从港口P出发,沿南偏东60°方向,以18海里/时的速度驶离港口,现两船同时出发.
(1)出发后几小时两船与港口P的距离相等?
(2)出发后几小时乙船在甲船的正东方向?(sin37°≈,cos37°≈,tan37°≈)
28.一艘海监船从A点沿正北方向巡航,其航线距某岛屿(设N、M为该岛屿的东西两端点)最近距离为15海里(即MC=15海里),在A点测得岛屿的西端点M在点A的东北方向,航行4海里后到达B点,测得岛屿的东端点N在点B的北偏东62°方向(其中N、M、C在同一条直线上),求该岛屿东西两端点MN之间的距离.(精确到0.1海里)(参考数据:sin62°≈0.88,cos62°≈0.47,tan62°≈1.87)
29.如图,一艘轮船原计划从A地直接航行到B地,两地间的距离AB为200km.后来了解到在两地之间的某一海域有暗礁,为了避开暗礁,轮船从A地出发后,就沿与水平线成30°角的方向航行,到达C地后再沿与水平线成45°角的方向继续航行直到B地.请问轮船这样航行的路程比原计划的路程远了多少?(要求在结果化简后再代入参考数据运算,最终结果精确到1km;参考数据:≈1.73,≈1.41).
30.如图,某渔船在完成捕捞作业后准备返回港口C,途经某海域A处时,港口C的工作人员监测到点A在南偏东30°方向上,另一港口B的工作人员监测到点A在正西方向上.已知港口C在港口B的北偏西60°方向,且B、C两地相距120海里.
(1)求出此时点A到港口C的距离(计算结果保留根号);
(2)若该渔船从A处沿AC方向向港口C驶去,当到达点A'时,测得港口B在A'的南偏东75°的方向上,求此时渔船的航行距离(计算结果保留根号).
参考答案
1.解:(1)由题意可知,AB=20×16=320海里,∠BAC=90°﹣60°,
过点B作BM⊥AC,垂足为M,
在Rt△ABM中,AB=320海里,∠BAM=30°,
∴BM=×320=160(海里)<200海里,
AM=×320=160海里,
∴B处会受到台风的影响,
故答案为:会;
(2)设台风初次影响B处时,此时台风中心为N,则BN=200海里,如图,
在Rt△BMN中,BN=200海里,BM=160海里,
∴MN===120(海里),
∴AN=AM﹣MN=(160﹣120)海里,
因此需要的时间为:=(8﹣6)小时,
故答案为:8﹣6.
2.解:如图,过C作CE⊥BA于E.
设EC=xm,BE=ym,
在Rt△ECB中,tan53°=≈,
即≈①,
在Rt△AEC中,tan37°=≈,
即≈②,
由①②得:x=120,y=90,
∴EC=120m,BE=90m,
∴AE=70+90=160(m),
∴AC===200(m),
故答案为:200.
3.解:如图,分别延长BC,ED交于F,
由题意得,∠B=90°,∠A=30°,∠BED=60°,
∴∠ADE=∠BED﹣∠A=30°,∠F=90°﹣∠BED=30°,
∵∠CDF=∠ADE=30°,
∴∠CDF=∠F,
∴CD=CF,
在Rt△BEF中,∠BED=60°,BE=45海里,
∴BF=BE tan60°=45(海里),
∴CF=BF﹣BC=(45﹣60)(海里),
∴CD=(45﹣60)海里,
答:此时乙船与C码头之间的距离为(45﹣60)海里.
4.解:(1)过点C作CD⊥AB于点D,
由题意得,∠A=30°,∠BCE=75°,AC=600m,
在Rt△ACD中,∠A=30°,AC=600,
∴CD=AC=300(m),
AD=AC=300(m),
∵∠BCE=75°=∠A+∠B,
∴∠B=75°﹣∠A=45°,
∴CD=BD=300(m),
BC=CD=300(m),
答:景点B和C处之间的距离为300m;
(2)由题意得.
AC+BC=(600+300)m,
AB=AD+BD=(300+300)m,
AC+BC﹣AB=(600+300)﹣(300+300)
≈204.6
≈205(m),
答:大桥修建后,从景点A到景点B比原来少走约205m.
5.解:作DE⊥AB于E,CF⊥DE于F,
∵BC⊥AB,
∴四边形BCFE是矩形,
∴BE=CF,EF=BC=150
m,
设DF=xm,则DE=(x+150)m,
在Rt△ADE中,∠BAD=30°,
∴AD=2DE=2(x+150)m,
在Rt△DCF中,∠FCD=22.6°,
∴CD=≈=xm,
∵AD=CD+BC,
∴2(x+150)=+150,
解得x=250(m),
∴DF=250
m,
∴DE=250+150=400
m,
∴AD=2DE=800
m,
∴CD=800﹣150=650
m,
由勾股定理得AE===400
m,
BE=CF===600
m,
∴AB=AE+BE=400+600≈1293(m),
答:公园北门A与南门B之间的距离约为1293
m.
6.解:如图,过点C作CH⊥AB于H.
∵∠AHC=90°,∠CAH=45°,
∴∠ACH=∠CAH=45°,
∴AH=CH,
设AH=CH=xnmile,
在Rt△CBH中,∠CHB=90°,∠CBH=30°,
∴BC=2CH=2x(nmile),BH=CH=x(nmile),
∵AB=AH+BH=30nmile,
∴x+x=30,
∴x=15(﹣1),
∴BC=2x=30(﹣1)≈21(nmile).
7.解:过D作DE⊥AB于E,DF⊥BC于F,如图所示:
由题意得:∠CDF=37°,CD=200米,
在Rt△CDF中,sin∠CDF==sin37°≈0.60,cos∠CDF==cos37°≈0.80,
∴CF≈200×0.60=120(米),DF≈200×0.80=160(米),
∵AB⊥BC,DF⊥BC,DE⊥AB,
∴∠B=∠DFB=∠DEB=90°,
∴四边形BFDE是矩形,
∴BF=DE,BE=DF=160米,
∴AE=AB﹣BE=300﹣160=140(米),
在Rt△ADE中,tan∠DAE==tan65°≈2.14,
∴DE≈AE×2.14=140×2.14=299.60(米),
∴BF=DE≈299.60(米),
∴BC=BF+CF=299.60+120≈420(米),
答:革命纪念碑与党史纪念馆之间的距离约为420米.
8.解:(1)设AD与BC交于点F,
由题意得BE∥AD,
∵BE∥AD且∠EBF=60°,
∴∠BFA=∠EBF=60°,
∵∠BFA=∠C+∠CAD且∠CAD=30°,
∴∠C=∠BFA﹣∠CAD=30°;
(2)过点B作BG⊥AD于G.
∵BG⊥AD,
∴∠AGB=∠BGD=90°,
在Rt△AGB中,AB=20米,∠BAG=45°,
AG=BG=20×sin45°=(米),
在Rt△BGF中,∠BFG=60°,
∴BF===(米),FG=BGtan60°===(米),
∵∠C=∠CAD=30°,
∴CF=AF=AG+FG=(10+)(米),
∴BC=BF+CF=(10+10)米,
答:两棵银杏树B、C之间的距离为(10+10)米.
9.解:如图,过Q作QC⊥AP于C,
由题意知,QB⊥AB,PA⊥AB,∠PAQ=63.5°,∠ABP=45°,AB=300米,
∴∠BAP=∠ABQ=90°,
∴AP∥BQ,
∴四边形ACQB是矩形,
∴∠AQB=∠PAQ=63.5°,AC=BQ,CQ=AB=300(米),
在Rt△ABP中,∠ABP=45°,
∴PA=AB=300米,
在Rt△ABQ中,tan63.5°=,
∴BQ≈=150(米),
∴PC=150米,
∴PQ==150≈335(米),
故医院与大厦的直线距离有335米.
10.解:过点A作AD⊥BC于D,
由题意知,∠ABC=28°+25°=53°,∠ACB=59°﹣28°=31°,BC=232km,
设AD=x,
在Rt△ABD中,∵∠ABD=53°,
∴BD==≈x,
在Rt△ACD中,∵∠ACD=30°,
∴CD===x,
∵BD+CD=BC,
∴x+x=232,
解得:x=96,
∴AD=96(km),
∴AC=2AD=192(km),
∴192÷24=8(h),
∴9+8=17,
答:“雪龙2”船大约17点钟到达C岛.
11.解:过点C作CD⊥AB于点D,如图所示:
则∠CAD=90°﹣60°=30°,∠CBD=45°,AD==CD,BD==CD,
∵AD+BD=AB,
∴(+1)CD=200km,
∴CD=100(﹣1)km,
在Rt△ACD中,AC=200(﹣1)km,
在Rt△BCD中,BC=100(﹣1),
AC+BC=200(﹣1)+100(﹣1)≈249(km),
249﹣200=49(km),
答:飞机的飞行路程比原来的路程远了约49km.
12.解:(1)过C作CE∥OA,如图所示:
则∠ACE=∠CAO=26.5°,
即在小岛C看点A俯角大小是26.5°,
由题意得:∠DOB=90°,
∵∠DBO=49°,
∴∠BDO=90°﹣49°=41°,
∴点B在小岛D南偏西41°方向上,
故答案为:26.5°,南偏西41°;
(2)设B处距离码头O有xkm,
由题意得:AB=28×0.2=5.6(km),
则OA=AB+BO=(5.6+x)km,
在Rt△CAO中,∠CAO=26.5°,
∵tan∠CAO=,
∴OC=OA tan∠CAO=(5.6+x) tan26.5°≈(5.6+x)×0.50=(2.8+0.5x)km,
在Rt△DBO中,∠DBO=49°,
∵tan∠DBO=,
∴DO=BO tan∠DBO=x tan49°≈1.15x(km),
∵DC=DO﹣CO,
∴6.4=1.15x﹣(2.8+0.5x),
解得:x≈14.2(km).
答:B处距离码头O约14.2km.
13.解:(1)过点C作CD⊥AB交AB的延长线于D.
由题意可知,∠ACD=70°,∠BCD=37°,
∴∠ACB=∠ACD﹣∠BCD=33°,
故答案为33;
(2)如图,在Rt△BCD中,BC=30,∠BCD=37°,
∴BD=BC sin∠BCD≈18(海里),CD=BC cos∠BCD≈24(海里),
在Rt△ACD中,CD=24海里,∠ACD=70°,
∴AD=24 tan∠ACD≈66(海里),
∴航母的速度为(66﹣18)÷1.5=32(海里/时).
答:航母的速度为32海里/时.
14.解:如图,过点B作BD⊥AC,垂足为D,连接AB,
由题意得,AC=32×0.5=16(nmile),BC=20×0.5=10(nmile),∠α=30°,∠β=80°,
∴∠C=30°+(90°﹣80°)=40°,
在Rt△BCD中,
CD=BC cosC≈10×0.77=7.7(nmile),
BD=BC sinC≈10×0.64=6.4(nmile),
∴AD=AC﹣CD=16﹣7.7=8.3(nmile),
在Rt△ADB中,
AB==≈10.48(nmile),
答:点A,B间的直线距离约为10.48nmile.
15.解:过点O作OC⊥AB,垂足为C,则∠AOC=90°﹣60°=30°,
∠BOC=90°﹣45°=45°,
在Rt△AOC中,
OC=OA cos30°=8×=4(km),
在Rt△BOC中,
OB===4(km),
答:小华家到学校的距离OB为4km.
16.解:过B作BD⊥AC,垂足为D,过B作BE⊥AB,交AC于E.
Rt△ABD中,∠DAB=45°,AB=40×1=40(公里),
∴BD=ABsin45°=40×=20(公里),
Rt△CBD中,∠CBD=∠CBE+∠EBD=45°+16°=61°,
∴BC=≈=(公里),
答:此时汽车与古建筑相距公里.
17.解:如图,过点B作BD⊥AC于点D,
根据题意,得∠CBD=60°,CB=200,∠ABD=45°,
在Rt△CBD中,BD=CB cos60°=200×=100(千米),CD=CB sin60°=200×=100(千米),
在Rt△ABD中,AD=BD tan45°=100(千米),
∴(千米),
答:A地到C地之间高速公路AC长千米.
18.解:如图,过点D作DE⊥AB于E,过D作DF⊥BC于F,则四边形EBFD是矩形,
设DE=x,
在Rt△ADE中,∠AED=90°,
∵tan∠DAE=,
∴AE=≈,
∴BE=AB﹣AE=(400﹣)m,
又BF=DE=xm,
∴CF=BC﹣BF=(628﹣x)m,
在Rt△CDF中,∠DFC=90°,∠DCF=45°,
∴∠CDF=45°,
∴∠CDF=∠DCF,
∴DF=CF=(628﹣x)m.
又BE=DF,
即:400﹣=(628﹣x)m,
解得:x≈428.
答:点D到AB的距离约428m.
19.解:过M作MD⊥AN于D,如图所示:
由题意得:AB=100米,∠MAB=90°﹣60°=30°,∠MBD=90°﹣30°=60°,
∴∠AMB=∠MBD﹣∠MAB=30°,
∴∠MAB=∠AMB,
∴MB=AB=100(米),
在Rt△BDM中,∠BMD=90°﹣60°=30°,
∴BD=MB=50(米),
∴MD=BD=50(米),
答:小岛M到航线AN的距离为50米.
20.解:根据题意得:AB=10×2=20(海里),BC=海里,∠BAC=180°﹣35°﹣55°=90°,
∴AC2+AB2=BC2,
∴,
∴AC=30(海里),
∴乙船的航速为:30÷2=15(海里/时),
答:乙船的航速是15海里/时.
21.解:由题意可知:∠ACP=∠BCP=90°,∠APC=90°﹣60°=30°,∠BPC=45°.
在Rt△BPC中,∠BCP=90°,∠B=∠BPC=45°,
∴BC=PC=60米,
在Rt△ACP中,∠ACP=90°,∠APC=30°,
∵tan30°=,
∴AC=PC tan30°=tan30°×60=60×=20(米).
∴AB=AC+BC=(60+20)米,
答:教学楼A与办公楼B之间的距离是(60+20)米.
22.解:作CD⊥AB于点D,
由题意可得,
∠CAD=45°,∠CBD=90°﹣68°=22°,
设CD=x,
则AD=CD=x,BD=AB﹣AD=7﹣x,
∵tan∠CBD==,tan22°≈0.40,
∴0.40≈,
解得x=2,
∵AC=,BC=,
∴AC+BC≈+≈8.2(km),
答:新建管道的总长度是8.2km.
23.解:如图,延长AB、DC相交于点E,则∠E=90°,
在Rt△DEB中,∠D=∠DBE=45°,BD=15nmile,
∴DE=BE=BD sin45°=15(nmile),
198s=0.055h,
AB=30×0.055=1.65(nmile),
∴AE=AB+BE=1.65+15=16.65(nmile),
在Rt△ACE中,∠ACE=53°,
∴CE==≈12.4875(nmile),
∴CD=15﹣12.4875=2.5125(nmile),
∴甲船的速度为2.5125÷0.055=45.68≈46(nmile/h),
答:船甲的速度为46nmile/h.
24.解:如图,过O作OC⊥AB于点C,
由题意得:OC=9m,
在Rt△AOC中,∠AOC=45°,
∴∠OAC=45°,
∴AC=OC=9(m),
在Rt△BOC中,∠BOC=53°,
∴BC=OC tan∠BOC≈9×=12(m),
∴AB=AC+BC=9+12=21(m),
21÷1.5=14(m/s),
14m/s=50.4km/h>40km/h,
∴超速了.
25.解:如图,由题意知,AB=250m,BC=50m,
过点A作AE⊥BS,交BS的延长线于点E,过点C作CD⊥AE于点D,则四边形BCDE是矩形,
∴DE=BC=50(m),CD=BE,
在Rt△ABE中,AB=250m,∠ABE=53°,
∴BE=AB cos∠ABE≈250×=150(m),AE=AB sin∠ABE≈250×=200(m),
在Rt△ACD中,∠ADC=90°,AD=AE﹣DE=200﹣50=150(m),CD=BE=150(m),
∴AC=(m),
即旗杆底部A处与公寓楼底部C处之间的距离约为212米.
26.解:过点A作AD⊥BC于D,
由题意知,∠ABC=28°+25°=53°,∠ACB=58°﹣28°=30°,BC=248km,
设AD=x,
在Rt△ABD中,∵∠ABD=53°,
∴BD=,
在Rt△ACD中,∵∠ACD=30°,
∴CD=,
∵BD+CD=BC,
∴,
解得:x≈100,
∴AD=100(km),
∴AC=2AD=200(km),
∴200÷25=8(h),
∴9+8=17,
答:“雪龙2”船大约17点钟到达C岛.
27.解:(1)设出发后x小时两船与港口P的距离相等.
根据题意得81﹣9x=18x.
解得x=3.
故出发后3小时两船与港口P的距离相等.
(2)设出发后y小时乙船在甲船的正东方向,
此时甲、乙两船的位置分别在点C,D处.
连接CD,过点P作PE⊥CD,垂足为E.
则点E在点P的正南方向.
在Rt△CEP中,∠CPE=37°,
则PE=PC cos37°.
在Rt△PED中,∠EPD=60°,
则PE=PD cos60°.
则PC cos37°=PD cos60°.
则(81﹣9y)cos37°=18y cos60°.
,
解得y=4.
答:出发后4小时乙船在甲船的正东方向.
28.解:由题意可知:AB=4海里,∠CAM=45°,∠CBN=62°,∠ACN=90°.
在Rt△ACM中,
∵MC=15,∠CAM=45°,
∴(海里),
∵AB=4海里,
∴BC=AC﹣AB=15﹣4=11(海里),
在Rt△BCND中,
∵∠CBN=62°,
∴NC=BC tan∠CBN=11 tan62°≈11×1.87=20.57(海里),
∴MN=NC﹣MC=20.57﹣15=5.57≈5.6(海里),
答:该岛屿东西两端点MN之间的距离为5.6海里.
29.解:过点C作CD⊥AB于点D,则AD=,BD=,
∵AD+BD=AB,
∴(+1)CD=200,
∴CD=100(﹣1),
在Rt△ACD中,AC=200(﹣1),
在Rt△BCD中,BC=100(﹣1),
AC+BC=200(﹣1)+100(﹣1)≈250(km),
250﹣200=50(km),
答:轮船这样航行的路程比原计划的路程远了50km.
30.解:(1)如图所示:延长BA,过点C作CD⊥BA延长线于点D,
由题意可得:∠CBD=30°,BC=120海里,
则CD=BC=60海里,
∵cos∠ACD==cos30°=,
即=,
∴AC=40(海里),
答:此时点A到军港C的距离为40海里;
(2)过点A′作A′N⊥BC于点N,如图:
由(1)得:CD=60海里,AC=40海里,
∵A'E∥CD,
∴∠AA'E=∠ACD=30°,
∴∠BA′A=45°,
∵∠BA'E=75°,
∴∠ABA'=15°,
∴∠2=15°=∠ABA',
即A′B平分∠CBA,
∴A'E=A'N,
设AA′=x,则AE=AA',A'N=A′E=AE=x,
∵∠1=60°﹣30°=30°,A'N⊥BC,
∴A'C=2A'N=x,
∵A'C+AA'=AC,
∴x+x=40,
解得:x=60﹣20,
∴AA'=(60﹣20)海里,
答:此时渔船的航行距离为(60﹣20)海里.
