3.4简单机械(杠杆)习题精选(含解析)
文档属性
| 名称 | 3.4简单机械(杠杆)习题精选(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 科学 | ||
| 更新时间 | 2021-10-06 22:28:24 | ||
图片预览



文档简介
九年级上第三单元:3.4简单机械-杠杆习题精选
一、选择题
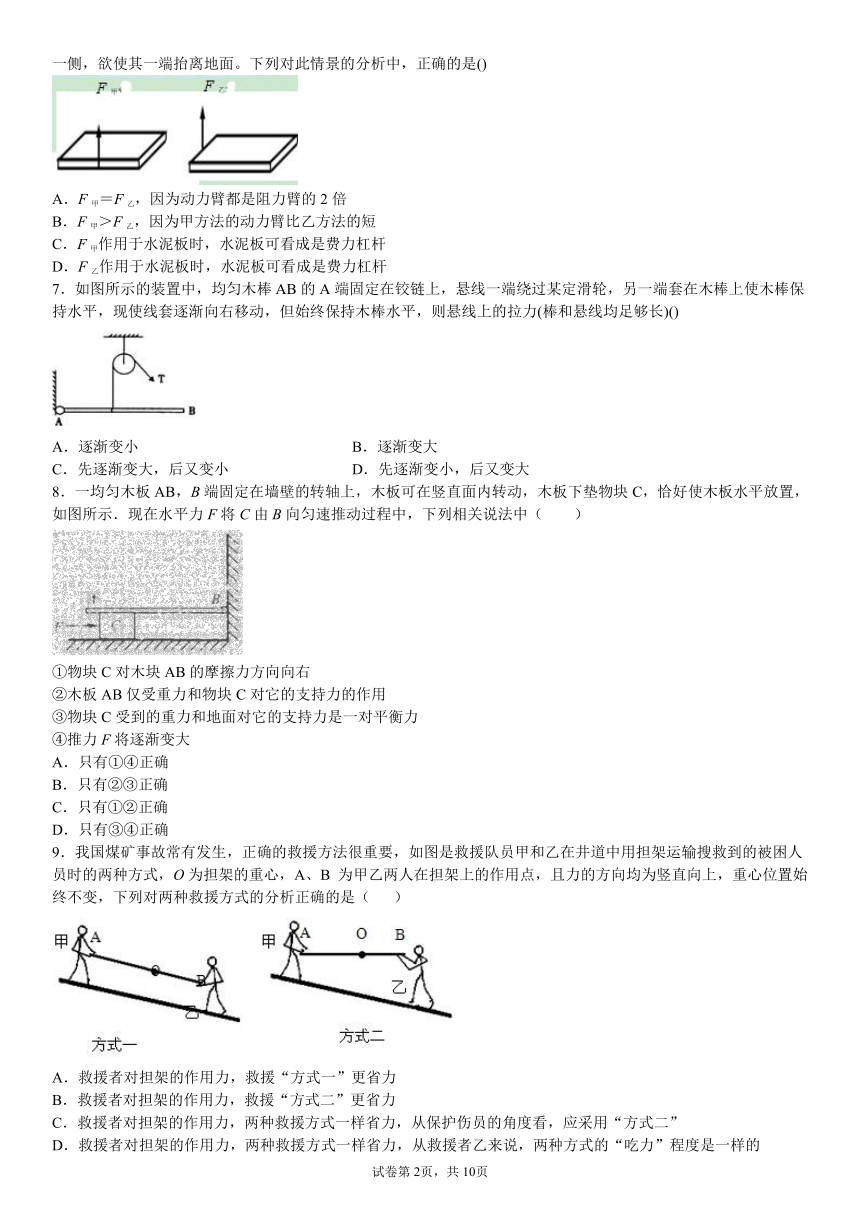
1.下列力臂的画法正确的是( )
A.B.C.
D.
2.有一圆柱铁块,想用如上甲乙两种方法使它倒下成丙图状。比较两种方法力和做功大小正确的是(
)
A.F1>F2W1>W2
B.F1C.F1=F2
W1=W2
D.F13.如上图,一根可绕O点转动的杠杆,在左端悬挂一重物,在A端通过绳子作用一竖直向下的拉力F,使杠杆平衡,此时AB部分处于水平位置,若重物保持静止,拉力F沿图中虚线顺时针或逆时针缓慢移动,则(
)
A.逆时针移动,拉力一直变小
B.顺时针移动,拉力一直变大
C.逆时针移动,拉力先变大后变小
D.顺时针移动,拉力先变大后变小
4.如图所示的杠杆中,OA=1m,OB=0.
4m,物体重力G=100N,杠杆自身重力忽略不计,则关于此杠杆,下列说法正确的是(
)
A.如图所示的杠杆的F1的力臂L1=1m
B.若使杠杆在如图所示位置平衡,则拉力F1=80N
C.F1的方向如图中实线所示时,杠杆在如图所示的位置平衡,则此时杠杆为费力杠杆
D.F1的方向从图示位置转到虚线所示的位置的过程中,F1逐渐变大
5.如图所示,可绕点转动的轻质杠杆,在点挂一个重为的物体,用一把弹簧测力计依次在,,三点沿圆相切的方向用力拉,都使杠杆在水平位置平衡,读出三次的示数分别为、、,它们的大小关系是
A.
B.
C.
D.
6.如图,一块厚度、密度均匀的长方形水泥板放在水平地面上,用一竖直向上的力分别作用于水泥板的长或宽的一侧,欲使其一端抬离地面。下列对此情景的分析中,正确的是()
A.F甲=F乙,因为动力臂都是阻力臂的2倍
B.F甲>F乙,因为甲方法的动力臂比乙方法的短
C.F甲作用于水泥板时,水泥板可看成是费力杠杆
D.F乙作用于水泥板时,水泥板可看成是费力杠杆
7.如图所示的装置中,均匀木棒AB的A端固定在铰链上,悬线一端绕过某定滑轮,另一端套在木棒上使木棒保持水平,现使线套逐渐向右移动,但始终保持木棒水平,则悬线上的拉力(棒和悬线均足够长)()
A.逐渐变小
B.逐渐变大
C.先逐渐变大,后又变小
D.先逐渐变小,后又变大
8.一均匀木板AB,B端固定在墙壁的转轴上,木板可在竖直面内转动,木板下垫物块C,恰好使木板水平放置,如图所示.现在水平力F将C由B向匀速推动过程中,下列相关说法中(
)
①物块C对木块AB的摩擦力方向向右
②木板AB仅受重力和物块C对它的支持力的作用
③物块C受到的重力和地面对它的支持力是一对平衡力
④推力F将逐渐变大
A.只有①④正确
B.只有②③正确
C.只有①②正确
D.只有③④正确
9.我国煤矿事故常有发生,正确的救援方法很重要,如图是救援队员甲和乙在井道中用担架运输搜救到的被困人员时的两种方式,O为担架的重心,A、B
为甲乙两人在担架上的作用点,且力的方向均为竖直向上,重心位置始终不变,下列对两种救援方式的分析正确的是(
)
A.救援者对担架的作用力,救援“方式一”更省力
B.救援者对担架的作用力,救援“方式二”更省力
C.救援者对担架的作用力,两种救援方式一样省力,从保护伤员的角度看,应采用“方式二”
D.救援者对担架的作用力,两种救援方式一样省力,从救援者乙来说,两种方式的“吃力”程度是一样的
10.如图所示,杠杆OBA可绕O点在竖直平面内转动,已知OB=40cm,AB=30cm,OB与AB垂直,忽略摩擦和杠杆重。一个重为200N、边长为10cm的正方体物体挂在OB的中点C处。下列说法正确的是( )
A.正方体物体的质量为2000kg
B.当外力作用在A端提重物时,杠杆OBA一定为省力杠杆
C.若用100N竖直向上的力作用在A端,此时正方体物体受到3个力的作用
D.若要使物体对地面的压强为6000Pa,则作用在A端的力至少为56N
11.如图所示,一根直硬棒被细绳系在O点吊起。A处挂一实心金属块甲,B处挂一石块乙时恰好能使硬棒在水平位置平衡。不计硬棒与悬挂的细绳质量,下列推断合理的是( )
A.甲的质量和密度都比乙大
B.O点绳子拉力一定等于甲、乙重力之和
C.如果甲浸没在水中,硬棒会逆时针转动
D.如果甲浸没在水中,要使硬棒水平平衡,可将乙向右移动
12.重为G的均匀硬棒悬于O点成竖直,现在下端施加一水平拉力F,让棒慢慢转过角,如图所示,则棒在转动过程中( )
A.拉力做功,拉力逐渐增大
B.拉力做功,拉力逐渐减小
C.拉力不做功,拉力逐渐增大
D.拉力不做功,拉力逐渐减小大
13.如图所示,OAB为杠杆,可绕支点O自由转动,在A处悬挂一重为G的物体,在B端施加一个动力使杠在水平位置平衡,下列说法正确的是(
)
A.所需动力一小于G
B.动力不可能水平向右
C.杠杆所受阻力就是重力所受重力
D.改变动力的方向,动力的大小一定改变
14.如图所示,一根可绕O点转动的均匀硬棒重为G,在棒的一端始终施加水平力F,将棒从图示。位置缓慢提起至虚线位置的过程中( )
A.F的力臂变小,F的大小变大
B.F的力臂变大,F的大小变小
C.重力G与它的力臂乘积保持不变
D.重力G与它的力臂乘积变大
15.如图所示,杠杆上各小格间距相等,O为杠杆中点,甲、乙是同种金属材料制成的实心物体,甲为正方体,乙重15N,将甲、乙用能承受最大拉力为20N的细线分别挂于杠杆上A、D两刻线处时,两细线被拉直且都沿竖直方向,A、D正好在甲、乙重心正上方,杠杆在水平位置平衡,这时甲对地面的压强为4000Pa;当把乙移挂至E时,甲对地面的压强甲为3750Pa。下列说法中正确的是( )
A.金属块甲的重力为40N
B.金属块乙的体积一定为200cm3
C.将甲向右移动并挂于B正下方,乙挂于E正下方,放手后杠杆能平衡
D.将甲向右移动并挂于C正下方,乙移挂至F,放手后甲被拉离地面
16.如图所示,一根质量分布均匀的木棒,能绕O处转轴自由转动(不计摩擦)。在木棒最下端用力,使之由A处缓慢地抬升到B处。下列说法合理的是(
)
A.始终水平方向的拉力F1大小将保持不变
B.始终与杆垂直的拉力F2大小将保持不变
C.始终竖直方向的拉力F3会逐渐增大
D.三次拉力抬升木棒的过程中所做的功均相等
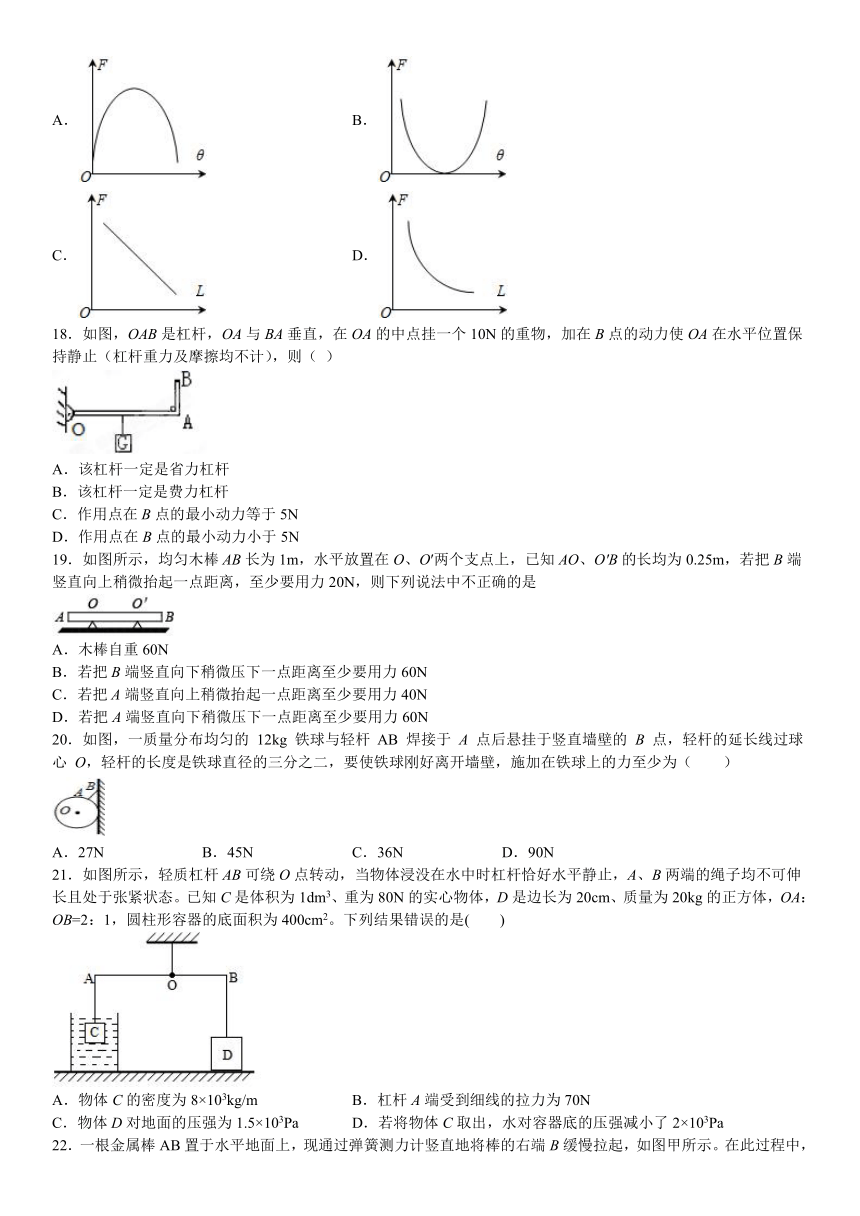
17.用图示装置探究杠杆的平衡条件。保持左侧的钩码个数和位置不变,使右侧弹簧测力计的作用点A固定,改变测力计与水平方向的夹角θ,则选项中关于动力F随夹角θ、动力臂L变化的关系图象中,可能正确的是(
)
A.
B.
C.
D.
18.如图,OAB是杠杆,OA与BA垂直,在OA的中点挂一个10N的重物,加在B点的动力使OA在水平位置保持静止(杠杆重力及摩擦均不计),则(
)
A.该杠杆一定是省力杠杆
B.该杠杆一定是费力杠杆
C.作用点在B点的最小动力等于5N
D.作用点在B点的最小动力小于5N
19.如图所示,均匀木棒AB长为1m,水平放置在O、O′两个支点上,已知AO、O′B的长均为0.25m,若把B端竖直向上稍微抬起一点距离,至少要用力20N,则下列说法中不正确的是
A.木棒自重60N
B.若把B端竖直向下稍微压下一点距离至少要用力60N
C.若把A端竖直向上稍微抬起一点距离至少要用力40N
D.若把A端竖直向下稍微压下一点距离至少要用力60N
20.如图,一质量分布均匀的
12kg
铁球与轻杆
AB
焊接于
A
点后悬挂于竖直墙壁的
B
点,轻杆的延长线过球心
O,轻杆的长度是铁球直径的三分之二,要使铁球刚好离开墙壁,施加在铁球上的力至少为(
)
A.27N
B.45N
C.36N
D.90N
21.如图所示,轻质杠杆AB可绕O点转动,当物体浸没在水中时杠杆恰好水平静止,A、B两端的绳子均不可伸长且处于张紧状态。已知C是体积为1dm3、重为80N的实心物体,D是边长为20cm、质量为20kg的正方体,OA:OB=2:1,圆柱形容器的底面积为400cm2。下列结果错误的是( )
A.物体C的密度为8×103kg/m
B.杠杆A端受到细线的拉力为70N
C.物体D对地面的压强为1.5×103Pa
D.若将物体C取出,水对容器底的压强减小了2×103Pa
22.一根金属棒AB置于水平地面上,现通过弹簧测力计竖直地将棒的右端B缓慢拉起,如图甲所示。在此过程中,弹簧测力计对棒所做的功W与B端离开地面的高度x的关系如图乙所示。根据图像,下列说法中正确的是(
)
A.该金属棒的长度L=1.6m
B.在B端拉起的过程中,当x1=0.6m时,测力计的示数为F1=1.5N
C.当x2=1.6m时,测力计的示数为F2=5N
D.金属棒的重心到A端的距离为0.6m
第II卷(非选择题)
请点击修改第II卷的文字说明
评卷人得分
二、填空题
23.如图所示,轻质杠杆OA中点悬挂一重G=60N的物体,在A端施加一竖直向上的力F,杠杆在水平位置平衡,则F= ________
N;保持F的方向不变,将杠杆从A位置匀速提到B位置的过程中,力F将________
。(填“变大”“不变”或“变小”)。
24.修车师傅对汽车的发动机做检修时要将引擎盖拉起,引擎盖的实图和模型如图所示。引擎盖可绕O点自由转动,A为引擎盖重心(可视为重力作用点)的位置。据此回答:
(1)若引擎盖所受重力为200牛,OA的距离为0.9米,OB的距离为1.2米,师傅对引擎盖在B点的作用力至少为______牛才能把引擎盖抬起。
(2)放下引擎盖后师傅发现双手抬引擎盖处的皮肤出现了凹痕,已知抬盖时引擎和双手的受力面积为,最小力抬住引擎盖时双手受到的压强为______。
25.如图所示是某同学设计的测量液体密度的装置。轻质杠杆AB可绕支点O自由转动,调节两侧螺母使杠杆在水平位置平衡。在杠杆左侧距离O点的C点用细绳悬挂一个质量为、容积为的小桶,小桶位置不变。在杠杆右侧用细绳悬挂一个质量为的钩码。
(1)在一次测量液体密度时,该同学向小桶中加满待测液体,并改变O点右侧钩码的悬挂位置,当钩码悬绳移至距O为的D点时,杠杆在水平位置平衡。则待测液体的密度为______。
(2)若让钩码在某位置保持不变,仍可用该装置测量液体的密度,即把对应密度值标在桶壁上,该刻度______(填“上”或“下”)边的数值大。
26.如图所示,用固定在墙上的三角支架ABC放置空调室外机。如果A处螺钉松脱,则支架会绕_______点倾翻。已知AB长0.4m,AC长0.3m。室外机的重力为300N,正好装在AB中点处,则A处螺钉的水平拉力为________N(支架重力不计)。为了安全,室外机的位置应尽量_______(填“靠近”或“远离”)墙壁。
27.如图所示,有一粗细均匀,重为40N,长为4m的长木板AB,置于支架上,支点为O,且,长木板的右端B用绳子系住,绳子另一端固定在C处,当长木板AB水平时,绳承受的最大拉力为60N。一个重为50N的体积不计的滑块M在的水平拉力作用下,从AO之间某处以的速度向B端匀速滑动,则:
(1)滑块匀速运动时所受的摩擦力的大小是______N;
(2)当滑块匀速运动时拉力F做功的功率是_______W;
(3)滑块在O点左侧______到右测_________范围内滑动才能使AB保持水平。
28.如图为油厂的油桶,空桶质量为65kg,油桶高为1.2m,底部直径为0.5m,据此回答。
(1)某次装卸中,小明需要将直立的空油桶(如图甲)沿D点推翻。在推翻油桶过程中,小明至少需要对油桶做功_____焦,
(2)若小明将直立的空油桶(如图甲)沿D点推翻,所需的最小力;将翻倒的空油桶(如图乙)重新竖起所用的最小力为,那么,____(选填“大于”、“等于”或“小于”)。
29.如图所示,两个完全相同的托盘秤甲和乙放在水平地面上。木条AB质量分布不均匀,A、B是木条两端,C、D是木条上的两个点,AD=BD,AC=DC。托盘秤甲和乙的中心各固定有一个大小和质量不计的小木块,A端放在托盘秤甲的小木块上,B端放在托盘秤乙的小木块上,甲的示数是6N,乙的示数是18N。物体AB的重力为________N;若移动托盘秤甲,让C点放在托盘秤甲的小木块上,则托盘秤乙的示数是________N。
30.小科同学用弹簧秤测量金属块的重力时,发现超出弹簧秤的量程,于是他设计了如图所示的装置去测量。图中,用细绳把金属块悬挂于A点,用弹簧秤在点施加一个竖直向上的力,当杠杆水平静止时,弹簧秤读数为。接着开始向容器中加水,当金属块浸没于水中后,弹簧秤读数为。金属块的密度为_______。
31.如图所示,有一长方体平台,轻质杆AD放在台面BC上,且AB=CD=,杆两端分别挂重物Ga和Gb,物重Ga=9N恒定不变,要使杆AD平衡,则
(1)杠杆水平平衡时a物体受到______力的作用(请写出a受到的所有力的名称)。
(2)平台台面BC受到的最大压力和最小压力之比为______。
32.一根均匀的长方体直棒重4牛,长1米,将它放在水平桌面上,用力F推直棒,直至有长度露出桌面外,如图所示。
(1)直棒受到的摩擦力在此过程中___________(选填“逐渐变大”、“逐渐变小”或“始终不变”)。
(2)现有一只重8牛的小球,以1米/秒的速度从直棒最左端A点向右运动,经过___________秒,直棒会顺时针翻转。
(3)小金在B端将直棒以最小力逆时针抬起30°,至少对直棒做功___________焦。
评卷人得分
三、简答题
33.小金在拓展课程活动中制作了一支可以测定物体密度的杆秤(杠杆自身重力不计)。使用时,只要把被测物体持在杆秤的挂钩上,移动秤锤,使秤杆在水平位置平衡,读出L1;再将被测物体浸没在密度为ρ的液体中,移动秆锤使秤杆再次水平平衡,读出L2,如图所示。
(1)请写出杠杆平衡的条件;
(2)被测物体的密度ρ物(用题目给出的量表示),试通过推导证明。
34.高压起重气垫是一种适合于地震救灾的起重工具,它由如图甲所示的高压气瓶、气管、阀门与气垫连接而成。起重时,气垫放入重物与地面的间隙之间,由高压气瓶向气垫内充气,气垫在短时间内可把重物举起一定高度,如图乙所示,质地均匀的长方体石板长2m,重为6×104N,当气垫气压高达106Pa时,石板恰好被顶起,此时气垫和石板的接触面积是400cm2。
(1)高压气瓶向气垫内充气时,气瓶内的气体温度______,内能______。
(2)如果高压起重气垫在5s内可将105N的重物举高0.1m,则其功率是多少______?
(3)气垫恰好顶起石板时,气垫的中心离石板右端的支点O多远______?
35.如图所示为测液体密度的密度秤示意图,轻质杆AB长为40cm,可绕O点转动(轻质杆与O点之间的摩擦忽略不计),其左端A点挂一个质量为0.2kg,容积为200mL的桶,AO=10cm;在O点的右侧用轻质细绳悬挂一个质量为0.2kg的秤砣,秤砣可沿OB左右滑动。使用时,在桶中装满待测液体,移动秤砣使密度秤再次水平平衡,读出相应位置的刻度值即可。
(1)密度秤零刻度在O点右侧______cm处。
(2)该密度秤所能测量的最大密度是多少______?
(3)判断该密度秤的刻度是否均匀______(通过推导说明)
36.如图所示,一位同学的质量为50kg,再将木棒支在O点,物体挂在A点,OB=1m,OA=0.2m。让该同学站在体重秤上用手将木棒抬到图示位置,此时体重秤的读数为60kg。试求(g取10N/kg):
(1)该同学单独测体重时,双脚与体重秤的接触面积为0.04m2,他对体重秤的压强为多大___________?
(2)该同学的手对杠杆B端的托力F为多大___________?
(3)求物体的重力为多大___________?
(4)若此时该同学用双手竖直向上匀速抬起木棒,体重秤的读数将___________(选填“增大”“不变”或“减小”)。
37.如图甲,有一轻质杆,左右各挂由同种金属制成、质量分别为和()的实心物块后恰好水平平衡。求:
(1)左右悬挂点到支点O的距离与之比_________。
(2)将两物分别浸没于水中(如图乙)杆将会_________(选填“左端下降”“右端下降”或“仍然平衡”),试通过推导说明_________。
试卷第2页,共2页
参考答案
1.C
【分析】
力臂是支点到力的作用线的距离。
【详解】
A.图中力臂在力的作用线上,不是力臂,A错误;
B.图中所示的力臂没有垂直于力的作用线,B错误;
C.图中力臂是从支点O到力F1作用线的距离,C正确;
D.图中力臂在力的作用线上,不是力臂,D错误。
故选C。
2.D
【详解】
如图
按照甲的方法,支点为B,F1力臂为BD;按照乙图方法,支点为C,F2力臂为D′C。因为BD大于D′C,用甲乙两种方法,阻力和阻力臂不变,故根据杠杆平衡条件可知,所用力的大小关系为:F1<F2。
无论如何将圆柱铁块倒下都是克服重力做功,两种方法使得柱体重心移动距离相等,故两个力做功相等,故比较使用甲乙两种方法,人至少要做的功的大小为:W1=W2。
故选D。
3.C
【详解】
由于阻力和阻力臂的乘积是一定的,杠杆要保持平衡,根据杠杆的平衡条件可知,动力臂越大,动力F就越小.由下图分析(注意看力臂的序号)可知顺时针时:动力臂先变大再变小,所以动力先变小再变大,故BD错误.
逆时针时:动力臂先变小再变大,所以动力先变大再变小,故A错误,C正确.
4.B
【分析】
A、根据力臂的概念结合三角函数得出L1的力臂;
B、得出L1的力臂,根据杠杆平衡条件计算出F1的大小;
C、根据动力臂与阻力臂的大小关系确定杠杆的种类;
D、根据动力臂的大小变化,由杠杆平衡条件分析动力的变化.
【详解】
A. F1的力臂如图所示:
则L1=OAsin=1m×=0.5m,A错误;
B.
若使杠杆在如图所示位置平衡,由F1L1=G OB得,
F1===80N,B正确;
C.
由A分析知,动力臂为0.5m,阻力臂为0.4m,动力臂大于阻力臂,动力小于阻力,为省力杠杆,C错误;
D. F1的方向从图示位置转到虚线所示的位置的过程中,动力臂变大,F1逐渐变小,D错误。
故选B.
5.C
【解析】
【详解】
设拉力的力臂为l,
根据杠杆的平衡条件F1l1=F2l2可知,
当杠杆在水平位置平衡时:Fl=GlOD,
则拉力F=,
因为G,lOD不变,lOD=l=r,所以F=G,
由于F1、F2、F3的力臂都是圆的半径,故F1=
F2=
F3=G.
故C正确.
6.A
【解析】
【详解】
把木板看做一根杠杆,抬起一端,则另一端为支点;两次抬起木板时的情况如图所示(第一次动力臂较小):
两种情况下,动力克服的都是木板的重力,对于形状规则质地均匀的物体,其重心都在其几何中心上,所以阻力臂都等于动力臂的二分之一,都是省力杠杆,故CD错误A正确;
根据杠杆的平衡条件可得F=GL阻L动=G,所以前后两次所用的力相同,故B错误。
7.D
【解析】
如图所示,G表示杆AB的自重,LOA表示杆的重心到A端的距离,T表示悬线拉力的大小,L表示作用于杆AB上的悬线拉力对A点的力臂.
把AB视为一根可绕A端转动的杠杆,则由杠杆的平衡条件应有:,
由此得:当线套在杆上逐渐向右移动时,拉力T的动力L(L1、L2、L3、L4)经历了先逐渐变大后又逐渐变小的过程,故悬线的拉力T则是逐渐变小后逐渐变大.故D正确,ABC错误.
故选:D.
【点睛】本题考查力矩平衡条件,当阻力和阻力臂的乘积一定时,分析省力情况就要看动力臂的大小变化,所以本题画出图中动力臂是解决本题的关键。
8.A
【详解】
①物块C向右移动时,水平方向上受向右的推力,水平面向左的摩擦力和AB对C向左的摩擦力,因为物体间力的作用是相互的,所以C对木板AB的摩擦力是向右的,故①正确;
②木板AB在竖直方向上受重力和物块C对它的支持力的作用,在水平方向上受木块C对它向右的摩擦力,故②错误;
③物块C受到的重力、地面对它的支持力以及木板AB对它的压力,所以物块C受到的重力和地面对它的支持力不是一对平衡力,故③错误;
④以杆为研究对象,杆受重力G和C对它的支持力F支,两力臂如图所示:
根据杠杆平衡条件可得:F支 L支=G LG,
水平力F由A向B缓慢匀速推动木块,F支的力臂在减小,重力G及其力臂LG均不变,
所以根据杠杆平衡条件可知,在整个过程中支持力在逐渐增大;
由于支持力逐渐变大,且力的作用是相互的,所以可知杆对物体C的压力也逐渐变大,
根据影响摩擦力大小的因素可知,C和木板间、C和地面间的摩擦力逐渐增大,由力的平衡条件知,水平推力F也逐渐增大,故④正确。
综合分析只有①④正确。
故A符合题意。
9.C
【详解】
以A点为支点,阻力为担架的总重力,阻力作用在O点;由下图可知,方式一:由A为支点,阻力臂为AC,动力臂为AD,由相似三角形的性质可得:
=
根据杠杆平衡条件可得:
F乙 AD=G AC
则
F乙=G=G------①
由上图可知,方式二:由A为支点,根据杠杆平衡条件可得:
F乙′ AB=G AO
则
F乙′=G------②
比较①②两式可知,F乙′=F乙;所以,两种救援方式一样省力,从保护伤员的角度看,应采用“方式二”故选C。
10.D
【详解】
A.物体的质量
m===20kg
故A错误;
B.当外力作用在A端提重物时,由于动力的方向不确定,所以动力臂和阻力臂的大小关系不能确定,自然不一定为省力杠杆,故B错误;
C.若用100N竖直向上的力作用在A端,阻力臂
OC==
动力臂OB=40cm,
由杠杆平衡条件可得
FB×OB=FC×OC
即
100N×40cm=FC×20cm
则杠杆C处受到的拉力:FC=200N,
由于力的作用是相互的,则杠杆对物体向上的拉力也为200N,那么这个拉力正好和物体的重力平衡,所以此时正方体物体不受支持力,只受到重力和拉力2个力的作用,故C错误;
D.要作用在A端的力最小,动力臂应最大,如下图,以OA为动力臂,垂直OA向上施加的力最小,
在直角三角形ABO中
OA==50cm
若使物体对地面的压强为6000Pa,则物体对地面的压力:
F压=pS=6000Pa×=60N
所以杠杆对物体的拉力
F拉=G-F压=200N-60N=140N
由杠杆平衡条件可得
FA×OA=FC×OC
即
FA×50cm=140N×20cm
解得:FA=56N,故D正确。
故选D。
11.B
【详解】
A.根据杠杆的平衡条件知,OA>OB,所以FAB.图中杠杆保持静止,受力平衡,所以O点绳子向上的拉力一定等于甲、乙重力之和,故B正确;
C.如果甲浸没在水中,受到浮力的作用,FA会减小,硬棒会顺时针转动,故C错误;
D.如果甲浸没在水中,受到浮力的作用,FA会减小,lA不变,FB不变,根据杠杆平衡条件得,要使硬棒水平平衡,lB应减小,即可将乙向左移动,故D错误。
故选B。
12.A
【详解】
由图示知道,在力F的方向通过了距离,由W=Fs知道,拉力做了功;杠杆在转动的过程中符合杠杆平衡的条件,即阻力为硬棒的重力,大小不变,硬棒在竖直位置时,重力的力臂为0,转过θ角后,重力力臂(阻力臂)逐渐增大,动力臂变小;由杠杆平衡的条件知道,阻力与阻力臂的乘积增大,而动力臂减小,所以拉力逐渐增大,故A符合题意。
故选A。
13.B
【详解】
A.在B端施加动力使杠杆在水平位置平衡,B点动力的方向不同时,动力臂可能大于或小于或等于阻力臂,所以该杠杆可能省力,可能费力,还可能既不省力也不费力,故A错误;
B.由于动力的方向水平向右时,动力臂为零,而阻力和阻力臂的乘积不为零,所以,杠杆不可能平衡,则动力的方向不可能水平向右,故B正确;
C.阻力是阻碍杠杆转动的力,本题中杠杆所受阻力是重物对杠杆向下的拉力,故C错误;
D.在阻力和阻力臂一定时,若施加动力的方向不同,动力臂也可能相同,根据杠杆平衡条件知道,动力的大小可能相同,故D错误。
故选B。
14.B
【分析】
力臂是从杠杆的支点到力的作用线之间的垂线段的长度;根据杠杆的平衡条件F1L1=F2L2分析即可。
【详解】
如下图所示,
根据杠杆的平衡条件得到
G×L2=F×L1
即
G×OA×cosα=F×OB×sinα
当∠α增大时,cosα变小,而sinα变大;
因此重力和它的力臂乘积变小,故C、D错误;
因为OB×sinα变大,所以动力F的力臂变大,而F却变小,故B正确,A错误。
15.C
【详解】
A.设甲的重力为G,甲的底面积为S,杠杆上1小格为L,则根据杠杆平衡条件可得
F甲×6L=G乙×2L
F甲×6L=15N×2L
解得F甲=5N,此时甲对地面的压强为
p==4000Pa
同理可得
F甲′×6L=15N×3L
解得F甲′=7.5N,此时甲对地面的压强为
p′==3750Pa
两式联立解得G=45N,故A错误;
B.甲的底面积为
S==0.01m2
甲是正立方体,边长为
=0.1m
故其体积为
V甲=(0.1m)3=0.001m3
又因为
G甲∶G乙=ρV甲g∶ρV乙g=V甲∶V乙=45N∶15N=3∶1
故乙的体积为
V乙=×0.001m3≈0.00033m3=330cm3
故B错误;
C.如果将甲向右移动并挂于B正下方,乙仍挂于E,此时
F′×4L=G乙×3L
F′×4L=15N×3L
解得
F'=11.25N<20N
所以放手后杠杆仍能平衡,故C正确;
D.将甲向右移动并挂于C正下方,乙移挂至F,假设杠杆平衡,则
F″×2L=G乙×7L
F″×2L=15N×7L
解得
F''=52.5N>20N
所以放手后细线拉力会大于20N,细线会断,则甲不会被拉离地面,故D错误。
故选C。
16.D
【详解】
分析杠杆的五要素,如如图所示:。
A.设杠杆与竖直方向的夹角为θ,F1的力臂
L1=cosθ×OA
重力的力臂
根据杠杆的平衡条件
因θ变大时,F1也变大,A错误。
B.F2与杠杆垂直,动力臂大小等于OA,保持不变,杠杆的G不变,在上升的过程中,阻力臂变大,根据杠杆的平衡条件,F2逐渐变大,B错误;
C.F3始终沿即沿竖直方向,由图可知,动力臂始终是阻力臂的2倍,根据杠杆的平衡条件,F3始终等于,故C错误。
D.由功的原理,使用任何机械不省功,三次拉力抬升木棒的过程中所做的功均相等,D正确。
故选D。
17.D
【详解】
A.动力F和θ的关系,当从水平→90°→水平,F对应的动力臂,先变小后变大,所以A错误。
B.当θ等于90°时动力最小但不为零,所以B错误。
CD.根据杠杆平衡条件
FL=F2L2
得
则F和L成反比,所以C错误,D正确。
故选D。
18.D
【解析】
【详解】
AB.因无法确定动力臂的大小,所以无法确定它是哪种杠杆,故A和B错误;
CD.加在B点的动力F与OB垂直向上时,动力作用线和杠杆垂直,支点与动力作用点之间的连线OB就是最长的动力臂,此时动力最小。因为C点是中点,所以OB>OA=2OC。
根据杠杆的平衡条件,此时的最小动力:
所以选项C错误,选项D正确。
19.C
【详解】
A.
如图1,支点为,,,
木棒平衡,
,
,
故A正确,不符合题意;
B.
如图2,支点为,,,
木棒平衡,
,
,
故B正确,不符合题意;
C.
如图3,支点为,,,
木棒平衡,
,
,
故C错误,符合题意;
D.
如图4,支点为,,,
木棒平衡,
,
,
故D正确,不符合题意。
20.B
【详解】
铁球的重力
G=mg=12kg×10N/kg=120N
由图知,当力F作用在球的下边缘,且与通过AB的直径垂直时,动力臂最长,其受力图如图所示
把整体看做一个杠杆,支点在B点,由图知,球的重力方向竖直向下,力臂为LG,由图知
LG=R
F的力臂等于杆的长度与球的直径之和,则
根据杠杆的平衡条件得
G LG=F LF
代入数据
解得
F=45N
故选B。
21.D
【分析】
A.已知物体的重力和体积,根据公式ρC=求物体C的密度。
B.利用阿基米德原理求受到的浮力,再根据杠杆A端受到的拉力等于C的重力减去浮力计算即可。
C.利用杠杆平衡条件F1L1=F2L2求杠杆B端受到细线的拉力,由于力的作用是相互的,可求杠杆B端对D的拉力,D对地面的压力等于D的重力减去拉力,利用压强公式计算D对地面的压强。
D.物体C浸没在水中前后,水的深度变化等于排开水的体积除以底面积,再利用p=ρgh求水对容器底的压强增大值。
【详解】
A.物体C的密度
ρC===8×103kg/m3
故A正确不合题意。
B.物体受到的浮力
F浮=ρ水gV排=1×103kg/m3×10N/kg×1×10-3m3=10N
杠杆A端受到的拉力
FA=GC-F浮=80N-10N=70N
故B正确不合题意。
C.由杠杆平衡条件F1L1=F2L2得
FA×OA=FB×OB
70N×2=FB×1
解得
FB=140N
由于力的作用是相互的,杠杆B端对D的拉力
F拉=FB=140N
对地面的压力
F压=GD-FB=mDg-F拉=20kg×10N/kg-140N=60N,
对地面的压强
p===1.5×103Pa
故C正确不合题意。
D.物体C浸没在水中前后,水的深度变化
h====2.5cm=0.025m
水对容器底的压强增大值
p=ρ水g h=1×103kg/m3×10N/kg×0.025m=2.5×102Pa
故D错误符合题意。
故选D。
22.C
【详解】
A.由于拉力始终竖直向上,由杠杆的平衡条件可知,拉力不变(动力臂与阻力臂之比不变)。
由图乙可知,当B端离地1.2m时,A端刚离地,所以金属棒长1.2米,故A错误;
BC.因为
W=Gh
所以金属棒的重力
即
F2=5N
杆未离地前,动力臂与阻力臂的比值不变,拉力大小不变,
由图乙可知拉力
故B错误、C正确。
D.由杠杆平衡条件得重心到A端的距离
故D错误。
故选C。
23.30;
不变
【分析】
杠杆静止不动或匀速转动都叫做杠杆平衡,本题应用杠杆的平衡条件来求解,关键是找到动力臂和阻力臂,在OA位置很容易看出:OA为动力臂,G对杠杆的向下拉力F2=G对应的力臂为1/2
OA,据动力×动力臂=阻力×阻力臂。
【详解】
由于重物悬挂在杠杆AO的中点上,所以力F的力臂LF是重力G的力臂LG的2倍,即LF=2LG.根据杠杆的平衡条件得,F==30
N.在杠杆由A到B的过程中,重力的大小和方向都没有变化,而两个力臂都发生了变化.但是在变化的过程中两个力臂之间始终保持着LF=2LG的关系,所以力F将保持不变。
【点睛】
分析本题杠杆的动态平衡时,应该动中取静,根据杠杆平衡条件,分析比较,得出结论。
24.150
75000
【详解】
(1)[1]根据杠杆的平衡条件得到
G×OA=F×OB
F==150N
(2)[2]最小力抬住引擎盖时双手受到的压强
=75000Pa
25.0.8
下
【详解】
(1)[1]容器的质量为m1,钩码的质量为m2,容器中液体的质量为m,根据杠杆的平衡条件得
G总×OC
=G砝码×OD
(m1+m)g×OC=m2g×OD
则液体的密度
(2)[2]若让砝码位置不变即质量不变,根据
可知:体积小的密度大,所以下边的刻度对应的数值大。
26.C
200
靠近
【详解】
[1]三角支架ABC可看作杠杆,C点是支点,如果A处螺钉松脱,则支架会绕C点倾翻;
[2]空调受到重力而作用在支架上的压力是阻力,这个压力大小等于空调机的重力大小,阻力臂为AB,动力臂为AC,根据杠杆的平衡条件,
A处螺钉的水平拉力为
;
[3]由杠杆的平衡条件
FA×AC=G×L阻
室外机对支架的作用力大小等于重力,是一定的,AC也是定值,为了安全,即应减小处螺钉的水平拉力FA的大小,应减小L阻大小,故室外机的位置应尽量靠近墙壁。
27.10
10
0.8m
1m
【分析】
(1)物体匀速直线运动时处于平衡状态,水平方向受到的两个力为平衡力,根据二力平衡条件求出滑块匀速运动时所受的摩擦力的大小。
(2)根据求出当滑块匀速运动时拉力F做功的功率。
(3)当M在O点左侧且绳子的拉力为0时,根据杠杆的平衡条件得出滑块水平平衡的最左侧位置;当在O点右侧且拉力为60N时,根据杠杆的平衡条件得出滑块在O点最右侧的位置,即可得出滑块移动的范围,要注意均匀杠杆的重心位于几何中心上。
【详解】
(1)[1]滑块匀速运动时处于平衡状态,水平方向的拉力和受到的摩擦力是一对平衡力,则根据二力平衡条件可知
(2)[2]当滑块匀速运动时拉力F做功的功率
(3)[3]设AB的中点为C,当M在O点左侧离O点米,绳子的拉力T=0时,如下图所示:
根据杠杆平衡条件则有
解得:;
[4]当M在O点右侧离O点米时,绳子的拉力T=60N,如下图所示:
根据杠杆平衡条件则有
解得:;
故滑块在O点左侧0.8m到右侧1m范围内滑动才能使AB保持水平。
28.32.5
小于
【详解】
(1)[1]在阻力与阻力臂一定的情况下,动力臂越大,动力越小,由图示可知,AD是最大动力臂,过A与AD的垂直的力最小,如图所示
由几何知识可得
在推翻油桶过程中,小明至少需要对油桶做功
(2)[2]由图甲与图乙所示可知,两种情况下,最小推力的动力臂相等,两种情况下阻力相等,图甲的阻力臂小于图乙的阻力臂,由杠杆平衡条件可知,图甲中的推力小于图乙中的推力,即F1小于F2。
29.24
16
【详解】
[1]物体AB压在两托盘秤上,则两托盘秤的示数之和为物体的重力
G=6N+18N=24N
[2]以B为支点,设物体AB长度为L1,重力对应力臂为L2根据杠杆平衡条件,则开始时有
F甲L1=GL2①
当让C点放在托盘秤甲的小木块上后,甲托盘秤向上的支持力的力臂变为,重力力臂不变,则根据杠杆平衡条件有
②
有①②综合可得
得
则乙托盘秤示数为
30.3.5×103kg/m3
【详解】
用细绳把金属块悬挂于A点,用弹簧秤在B点施加一个竖直向上的力,当OB杠杆水平静止时,弹簧秤读数为2.1N,则根据杠杆平衡条件知道
F1 OB=FG OA
则
由于金属块受重力和拉力而处于平衡状态,所以,此金属块的重力
G=FG=6.3N
浸没水中后由杠杆平衡条件知道,
则
金属块此时受重力G、浮力F浮及拉力F′而处于平衡状态,即
G=F浮+F′
则金属块受到的浮力
F浮=G-F′=6.3N-4.5N=1.8N
由F浮=ρgV排知道,排开水的体积
由
知道,金属块的质量
由知道,金属块的密度
31.2
3∶1
【详解】
(1)[1]杠杆水平平衡时a物体受到两个力作用,分别是a的重力和绳子对a的拉力。
(2)[2]由图可知,以B为支点,根据杠杆平衡条件可得
Ga×AB=Gb×BD
由
AB=CD=BC
可得
2AB=BC,BD=3AB
Gb=
平台台面BC受到的最小压力
F小=Ga+Gb=9N+3N=12N
以C为支点,根据杠杆平衡条件可得
Ga×AC=Gb′×CD
由
AB=CD=BC
可得
2CD=BC,AC=3CD
平台台面BC受到的最大压力
F大=Ga+Gb=9N+27N=36N
32.始终不变
0.875
1
【详解】
(1)[1]用力F推直棒,直至有长度露出桌面外,压力和接触面的粗糙程度不变,摩擦力大小不变。
(2)[2]小球运动到D点时,直棒会顺时针翻转,如图所示:
OC的长度为
OC=1m×-1m×m=0.25m
OD的长度为
OD=1m×-(1m-vt)=1m/s×t-0.75m
由杠杆平衡条件得到
G×OC=F×OD
4N×0.25m=8N×(1m/s×t-0.75m)
t=0.875s
(3)[3]如图所示:
在B端将直棒以最小力逆时针抬起30°,至少对直棒做功等于克服重力做的功
W=Gh=G××AB=4N×××1m=1J
33.(1)F1L1=F2L2;(2)见解析
【详解】
解:(1)杠杆平衡的条件
F1L1=F2L2
(2)设被测物体的密度为ρ物,体积为V,挂物体处离提的距离为L0,秤锤重为G0,根据杠杆的平衡条件可得,空气中
ρ物VgL0=G0Ll------①
浸没在中后
(ρ物Vg-ρVg)L0=G0L2------②
由①、②两式解得
ρ物=
答:(1)杠杆平衡的条件F1L1=F2L2;
(2)被测物体的密度ρ物=。
34.降低
减小
2000W
1.5m
【详解】
(1)[1][2]高压气瓶向气垫内充气时,气体膨胀对外做功,内能减小,温度降低。
(2)[3]高压起重气垫做功
W=Gh=105N×0.1m=10000J
功率为
P===2000W
(3)[4]将石板当做杠杆如图:
气垫对石板的压力
F=pS=106Pa×400×10 4m2=40000N
质地均匀的长方体石板,所以,重心在中心,根据杠杆的平衡条件得到
F×OA=G×l2
气垫的中心离石板右端的距离
OA===1.5m
35.10
2×103kg/m3
见解析
【详解】
(1)[1]当小桶为空桶时移动秤砣至某点,设该点为E,此时密度秤正好水平平衡,小桶的质量为0.2kg,秤砣的质量为0.2kg,左侧的力臂为AO=10cm,则杠杆平衡条件F1l1=F2l2得
G桶OA=G砣OE
m桶gOA=m砣gOE
OE==10cm
即密度秤零刻度在O点右侧10cm处。
(2)[2]当右侧的力臂为
OB=AB-OA=40cm-10cm=30cm
时,该密度秤小桶所能测量液体的质量最大,则密度就最大,根据杠杆平衡条件得
(G桶+G液体)OA=G砣OB
(m桶+m液)gOA=m砣gOB
液体的质量
m液=×0.2kg-0.2kg=0.4kg=400g
液体的最大密度
ρ液最大=
(3)[3]液体的密度
由此可知:液体密度与提钮到秤舵的距离之间的关系是一次函数,因此密度秤的刻度是均匀的。
36.1.25×104Pa
100N
500N
不变
【详解】
(1)[1]对秤的压力为
F=G=mg=50kg×10N/kg=500N
对秤的压强为
p===1.25×104Pa
(2)[2]由题意知,体重计的示数变化为
m=60kg 50kg=10kg
根据力的作用的相互性可知,对B的提力
F=mg=10kg×10N/kg=100N。
(3)[3]根据杠杆的平衡条件可得
G×OA=F×OB
则
G===500N。
(4)[4]如果该同学用双手竖直向上匀速抬起木棒,物体的重力不变,动力臂和阻力臂的比值也不变,所以力F不变,则体重计显示的读数将不变。
37.m2∶m1
仍然平衡
见解析
【详解】
(1)[1]由杠杆平衡公式可得
则
l1∶l2=m2∶m1
(2)[2][3]浸入水中之后左边向下拉力
浸入水中之后右边向下拉力
则动力与动力臂乘积为
①
阻力与阻力臂乘积为
②
又由
得
则
故代入①②可得
杠杆依然保持平衡。
答案第1页,共2页
答案第1页,共2页
一、选择题
1.下列力臂的画法正确的是( )
A.B.C.
D.
2.有一圆柱铁块,想用如上甲乙两种方法使它倒下成丙图状。比较两种方法力和做功大小正确的是(
)
A.F1>F2W1>W2
B.F1
W1=W2
D.F1
)
A.逆时针移动,拉力一直变小
B.顺时针移动,拉力一直变大
C.逆时针移动,拉力先变大后变小
D.顺时针移动,拉力先变大后变小
4.如图所示的杠杆中,OA=1m,OB=0.
4m,物体重力G=100N,杠杆自身重力忽略不计,则关于此杠杆,下列说法正确的是(
)
A.如图所示的杠杆的F1的力臂L1=1m
B.若使杠杆在如图所示位置平衡,则拉力F1=80N
C.F1的方向如图中实线所示时,杠杆在如图所示的位置平衡,则此时杠杆为费力杠杆
D.F1的方向从图示位置转到虚线所示的位置的过程中,F1逐渐变大
5.如图所示,可绕点转动的轻质杠杆,在点挂一个重为的物体,用一把弹簧测力计依次在,,三点沿圆相切的方向用力拉,都使杠杆在水平位置平衡,读出三次的示数分别为、、,它们的大小关系是
A.
B.
C.
D.
6.如图,一块厚度、密度均匀的长方形水泥板放在水平地面上,用一竖直向上的力分别作用于水泥板的长或宽的一侧,欲使其一端抬离地面。下列对此情景的分析中,正确的是()
A.F甲=F乙,因为动力臂都是阻力臂的2倍
B.F甲>F乙,因为甲方法的动力臂比乙方法的短
C.F甲作用于水泥板时,水泥板可看成是费力杠杆
D.F乙作用于水泥板时,水泥板可看成是费力杠杆
7.如图所示的装置中,均匀木棒AB的A端固定在铰链上,悬线一端绕过某定滑轮,另一端套在木棒上使木棒保持水平,现使线套逐渐向右移动,但始终保持木棒水平,则悬线上的拉力(棒和悬线均足够长)()
A.逐渐变小
B.逐渐变大
C.先逐渐变大,后又变小
D.先逐渐变小,后又变大
8.一均匀木板AB,B端固定在墙壁的转轴上,木板可在竖直面内转动,木板下垫物块C,恰好使木板水平放置,如图所示.现在水平力F将C由B向匀速推动过程中,下列相关说法中(
)
①物块C对木块AB的摩擦力方向向右
②木板AB仅受重力和物块C对它的支持力的作用
③物块C受到的重力和地面对它的支持力是一对平衡力
④推力F将逐渐变大
A.只有①④正确
B.只有②③正确
C.只有①②正确
D.只有③④正确
9.我国煤矿事故常有发生,正确的救援方法很重要,如图是救援队员甲和乙在井道中用担架运输搜救到的被困人员时的两种方式,O为担架的重心,A、B
为甲乙两人在担架上的作用点,且力的方向均为竖直向上,重心位置始终不变,下列对两种救援方式的分析正确的是(
)
A.救援者对担架的作用力,救援“方式一”更省力
B.救援者对担架的作用力,救援“方式二”更省力
C.救援者对担架的作用力,两种救援方式一样省力,从保护伤员的角度看,应采用“方式二”
D.救援者对担架的作用力,两种救援方式一样省力,从救援者乙来说,两种方式的“吃力”程度是一样的
10.如图所示,杠杆OBA可绕O点在竖直平面内转动,已知OB=40cm,AB=30cm,OB与AB垂直,忽略摩擦和杠杆重。一个重为200N、边长为10cm的正方体物体挂在OB的中点C处。下列说法正确的是( )
A.正方体物体的质量为2000kg
B.当外力作用在A端提重物时,杠杆OBA一定为省力杠杆
C.若用100N竖直向上的力作用在A端,此时正方体物体受到3个力的作用
D.若要使物体对地面的压强为6000Pa,则作用在A端的力至少为56N
11.如图所示,一根直硬棒被细绳系在O点吊起。A处挂一实心金属块甲,B处挂一石块乙时恰好能使硬棒在水平位置平衡。不计硬棒与悬挂的细绳质量,下列推断合理的是( )
A.甲的质量和密度都比乙大
B.O点绳子拉力一定等于甲、乙重力之和
C.如果甲浸没在水中,硬棒会逆时针转动
D.如果甲浸没在水中,要使硬棒水平平衡,可将乙向右移动
12.重为G的均匀硬棒悬于O点成竖直,现在下端施加一水平拉力F,让棒慢慢转过角,如图所示,则棒在转动过程中( )
A.拉力做功,拉力逐渐增大
B.拉力做功,拉力逐渐减小
C.拉力不做功,拉力逐渐增大
D.拉力不做功,拉力逐渐减小大
13.如图所示,OAB为杠杆,可绕支点O自由转动,在A处悬挂一重为G的物体,在B端施加一个动力使杠在水平位置平衡,下列说法正确的是(
)
A.所需动力一小于G
B.动力不可能水平向右
C.杠杆所受阻力就是重力所受重力
D.改变动力的方向,动力的大小一定改变
14.如图所示,一根可绕O点转动的均匀硬棒重为G,在棒的一端始终施加水平力F,将棒从图示。位置缓慢提起至虚线位置的过程中( )
A.F的力臂变小,F的大小变大
B.F的力臂变大,F的大小变小
C.重力G与它的力臂乘积保持不变
D.重力G与它的力臂乘积变大
15.如图所示,杠杆上各小格间距相等,O为杠杆中点,甲、乙是同种金属材料制成的实心物体,甲为正方体,乙重15N,将甲、乙用能承受最大拉力为20N的细线分别挂于杠杆上A、D两刻线处时,两细线被拉直且都沿竖直方向,A、D正好在甲、乙重心正上方,杠杆在水平位置平衡,这时甲对地面的压强为4000Pa;当把乙移挂至E时,甲对地面的压强甲为3750Pa。下列说法中正确的是( )
A.金属块甲的重力为40N
B.金属块乙的体积一定为200cm3
C.将甲向右移动并挂于B正下方,乙挂于E正下方,放手后杠杆能平衡
D.将甲向右移动并挂于C正下方,乙移挂至F,放手后甲被拉离地面
16.如图所示,一根质量分布均匀的木棒,能绕O处转轴自由转动(不计摩擦)。在木棒最下端用力,使之由A处缓慢地抬升到B处。下列说法合理的是(
)
A.始终水平方向的拉力F1大小将保持不变
B.始终与杆垂直的拉力F2大小将保持不变
C.始终竖直方向的拉力F3会逐渐增大
D.三次拉力抬升木棒的过程中所做的功均相等
17.用图示装置探究杠杆的平衡条件。保持左侧的钩码个数和位置不变,使右侧弹簧测力计的作用点A固定,改变测力计与水平方向的夹角θ,则选项中关于动力F随夹角θ、动力臂L变化的关系图象中,可能正确的是(
)
A.
B.
C.
D.
18.如图,OAB是杠杆,OA与BA垂直,在OA的中点挂一个10N的重物,加在B点的动力使OA在水平位置保持静止(杠杆重力及摩擦均不计),则(
)
A.该杠杆一定是省力杠杆
B.该杠杆一定是费力杠杆
C.作用点在B点的最小动力等于5N
D.作用点在B点的最小动力小于5N
19.如图所示,均匀木棒AB长为1m,水平放置在O、O′两个支点上,已知AO、O′B的长均为0.25m,若把B端竖直向上稍微抬起一点距离,至少要用力20N,则下列说法中不正确的是
A.木棒自重60N
B.若把B端竖直向下稍微压下一点距离至少要用力60N
C.若把A端竖直向上稍微抬起一点距离至少要用力40N
D.若把A端竖直向下稍微压下一点距离至少要用力60N
20.如图,一质量分布均匀的
12kg
铁球与轻杆
AB
焊接于
A
点后悬挂于竖直墙壁的
B
点,轻杆的延长线过球心
O,轻杆的长度是铁球直径的三分之二,要使铁球刚好离开墙壁,施加在铁球上的力至少为(
)
A.27N
B.45N
C.36N
D.90N
21.如图所示,轻质杠杆AB可绕O点转动,当物体浸没在水中时杠杆恰好水平静止,A、B两端的绳子均不可伸长且处于张紧状态。已知C是体积为1dm3、重为80N的实心物体,D是边长为20cm、质量为20kg的正方体,OA:OB=2:1,圆柱形容器的底面积为400cm2。下列结果错误的是( )
A.物体C的密度为8×103kg/m
B.杠杆A端受到细线的拉力为70N
C.物体D对地面的压强为1.5×103Pa
D.若将物体C取出,水对容器底的压强减小了2×103Pa
22.一根金属棒AB置于水平地面上,现通过弹簧测力计竖直地将棒的右端B缓慢拉起,如图甲所示。在此过程中,弹簧测力计对棒所做的功W与B端离开地面的高度x的关系如图乙所示。根据图像,下列说法中正确的是(
)
A.该金属棒的长度L=1.6m
B.在B端拉起的过程中,当x1=0.6m时,测力计的示数为F1=1.5N
C.当x2=1.6m时,测力计的示数为F2=5N
D.金属棒的重心到A端的距离为0.6m
第II卷(非选择题)
请点击修改第II卷的文字说明
评卷人得分
二、填空题
23.如图所示,轻质杠杆OA中点悬挂一重G=60N的物体,在A端施加一竖直向上的力F,杠杆在水平位置平衡,则F= ________
N;保持F的方向不变,将杠杆从A位置匀速提到B位置的过程中,力F将________
。(填“变大”“不变”或“变小”)。
24.修车师傅对汽车的发动机做检修时要将引擎盖拉起,引擎盖的实图和模型如图所示。引擎盖可绕O点自由转动,A为引擎盖重心(可视为重力作用点)的位置。据此回答:
(1)若引擎盖所受重力为200牛,OA的距离为0.9米,OB的距离为1.2米,师傅对引擎盖在B点的作用力至少为______牛才能把引擎盖抬起。
(2)放下引擎盖后师傅发现双手抬引擎盖处的皮肤出现了凹痕,已知抬盖时引擎和双手的受力面积为,最小力抬住引擎盖时双手受到的压强为______。
25.如图所示是某同学设计的测量液体密度的装置。轻质杠杆AB可绕支点O自由转动,调节两侧螺母使杠杆在水平位置平衡。在杠杆左侧距离O点的C点用细绳悬挂一个质量为、容积为的小桶,小桶位置不变。在杠杆右侧用细绳悬挂一个质量为的钩码。
(1)在一次测量液体密度时,该同学向小桶中加满待测液体,并改变O点右侧钩码的悬挂位置,当钩码悬绳移至距O为的D点时,杠杆在水平位置平衡。则待测液体的密度为______。
(2)若让钩码在某位置保持不变,仍可用该装置测量液体的密度,即把对应密度值标在桶壁上,该刻度______(填“上”或“下”)边的数值大。
26.如图所示,用固定在墙上的三角支架ABC放置空调室外机。如果A处螺钉松脱,则支架会绕_______点倾翻。已知AB长0.4m,AC长0.3m。室外机的重力为300N,正好装在AB中点处,则A处螺钉的水平拉力为________N(支架重力不计)。为了安全,室外机的位置应尽量_______(填“靠近”或“远离”)墙壁。
27.如图所示,有一粗细均匀,重为40N,长为4m的长木板AB,置于支架上,支点为O,且,长木板的右端B用绳子系住,绳子另一端固定在C处,当长木板AB水平时,绳承受的最大拉力为60N。一个重为50N的体积不计的滑块M在的水平拉力作用下,从AO之间某处以的速度向B端匀速滑动,则:
(1)滑块匀速运动时所受的摩擦力的大小是______N;
(2)当滑块匀速运动时拉力F做功的功率是_______W;
(3)滑块在O点左侧______到右测_________范围内滑动才能使AB保持水平。
28.如图为油厂的油桶,空桶质量为65kg,油桶高为1.2m,底部直径为0.5m,据此回答。
(1)某次装卸中,小明需要将直立的空油桶(如图甲)沿D点推翻。在推翻油桶过程中,小明至少需要对油桶做功_____焦,
(2)若小明将直立的空油桶(如图甲)沿D点推翻,所需的最小力;将翻倒的空油桶(如图乙)重新竖起所用的最小力为,那么,____(选填“大于”、“等于”或“小于”)。
29.如图所示,两个完全相同的托盘秤甲和乙放在水平地面上。木条AB质量分布不均匀,A、B是木条两端,C、D是木条上的两个点,AD=BD,AC=DC。托盘秤甲和乙的中心各固定有一个大小和质量不计的小木块,A端放在托盘秤甲的小木块上,B端放在托盘秤乙的小木块上,甲的示数是6N,乙的示数是18N。物体AB的重力为________N;若移动托盘秤甲,让C点放在托盘秤甲的小木块上,则托盘秤乙的示数是________N。
30.小科同学用弹簧秤测量金属块的重力时,发现超出弹簧秤的量程,于是他设计了如图所示的装置去测量。图中,用细绳把金属块悬挂于A点,用弹簧秤在点施加一个竖直向上的力,当杠杆水平静止时,弹簧秤读数为。接着开始向容器中加水,当金属块浸没于水中后,弹簧秤读数为。金属块的密度为_______。
31.如图所示,有一长方体平台,轻质杆AD放在台面BC上,且AB=CD=,杆两端分别挂重物Ga和Gb,物重Ga=9N恒定不变,要使杆AD平衡,则
(1)杠杆水平平衡时a物体受到______力的作用(请写出a受到的所有力的名称)。
(2)平台台面BC受到的最大压力和最小压力之比为______。
32.一根均匀的长方体直棒重4牛,长1米,将它放在水平桌面上,用力F推直棒,直至有长度露出桌面外,如图所示。
(1)直棒受到的摩擦力在此过程中___________(选填“逐渐变大”、“逐渐变小”或“始终不变”)。
(2)现有一只重8牛的小球,以1米/秒的速度从直棒最左端A点向右运动,经过___________秒,直棒会顺时针翻转。
(3)小金在B端将直棒以最小力逆时针抬起30°,至少对直棒做功___________焦。
评卷人得分
三、简答题
33.小金在拓展课程活动中制作了一支可以测定物体密度的杆秤(杠杆自身重力不计)。使用时,只要把被测物体持在杆秤的挂钩上,移动秤锤,使秤杆在水平位置平衡,读出L1;再将被测物体浸没在密度为ρ的液体中,移动秆锤使秤杆再次水平平衡,读出L2,如图所示。
(1)请写出杠杆平衡的条件;
(2)被测物体的密度ρ物(用题目给出的量表示),试通过推导证明。
34.高压起重气垫是一种适合于地震救灾的起重工具,它由如图甲所示的高压气瓶、气管、阀门与气垫连接而成。起重时,气垫放入重物与地面的间隙之间,由高压气瓶向气垫内充气,气垫在短时间内可把重物举起一定高度,如图乙所示,质地均匀的长方体石板长2m,重为6×104N,当气垫气压高达106Pa时,石板恰好被顶起,此时气垫和石板的接触面积是400cm2。
(1)高压气瓶向气垫内充气时,气瓶内的气体温度______,内能______。
(2)如果高压起重气垫在5s内可将105N的重物举高0.1m,则其功率是多少______?
(3)气垫恰好顶起石板时,气垫的中心离石板右端的支点O多远______?
35.如图所示为测液体密度的密度秤示意图,轻质杆AB长为40cm,可绕O点转动(轻质杆与O点之间的摩擦忽略不计),其左端A点挂一个质量为0.2kg,容积为200mL的桶,AO=10cm;在O点的右侧用轻质细绳悬挂一个质量为0.2kg的秤砣,秤砣可沿OB左右滑动。使用时,在桶中装满待测液体,移动秤砣使密度秤再次水平平衡,读出相应位置的刻度值即可。
(1)密度秤零刻度在O点右侧______cm处。
(2)该密度秤所能测量的最大密度是多少______?
(3)判断该密度秤的刻度是否均匀______(通过推导说明)
36.如图所示,一位同学的质量为50kg,再将木棒支在O点,物体挂在A点,OB=1m,OA=0.2m。让该同学站在体重秤上用手将木棒抬到图示位置,此时体重秤的读数为60kg。试求(g取10N/kg):
(1)该同学单独测体重时,双脚与体重秤的接触面积为0.04m2,他对体重秤的压强为多大___________?
(2)该同学的手对杠杆B端的托力F为多大___________?
(3)求物体的重力为多大___________?
(4)若此时该同学用双手竖直向上匀速抬起木棒,体重秤的读数将___________(选填“增大”“不变”或“减小”)。
37.如图甲,有一轻质杆,左右各挂由同种金属制成、质量分别为和()的实心物块后恰好水平平衡。求:
(1)左右悬挂点到支点O的距离与之比_________。
(2)将两物分别浸没于水中(如图乙)杆将会_________(选填“左端下降”“右端下降”或“仍然平衡”),试通过推导说明_________。
试卷第2页,共2页
参考答案
1.C
【分析】
力臂是支点到力的作用线的距离。
【详解】
A.图中力臂在力的作用线上,不是力臂,A错误;
B.图中所示的力臂没有垂直于力的作用线,B错误;
C.图中力臂是从支点O到力F1作用线的距离,C正确;
D.图中力臂在力的作用线上,不是力臂,D错误。
故选C。
2.D
【详解】
如图
按照甲的方法,支点为B,F1力臂为BD;按照乙图方法,支点为C,F2力臂为D′C。因为BD大于D′C,用甲乙两种方法,阻力和阻力臂不变,故根据杠杆平衡条件可知,所用力的大小关系为:F1<F2。
无论如何将圆柱铁块倒下都是克服重力做功,两种方法使得柱体重心移动距离相等,故两个力做功相等,故比较使用甲乙两种方法,人至少要做的功的大小为:W1=W2。
故选D。
3.C
【详解】
由于阻力和阻力臂的乘积是一定的,杠杆要保持平衡,根据杠杆的平衡条件可知,动力臂越大,动力F就越小.由下图分析(注意看力臂的序号)可知顺时针时:动力臂先变大再变小,所以动力先变小再变大,故BD错误.
逆时针时:动力臂先变小再变大,所以动力先变大再变小,故A错误,C正确.
4.B
【分析】
A、根据力臂的概念结合三角函数得出L1的力臂;
B、得出L1的力臂,根据杠杆平衡条件计算出F1的大小;
C、根据动力臂与阻力臂的大小关系确定杠杆的种类;
D、根据动力臂的大小变化,由杠杆平衡条件分析动力的变化.
【详解】
A. F1的力臂如图所示:
则L1=OAsin=1m×=0.5m,A错误;
B.
若使杠杆在如图所示位置平衡,由F1L1=G OB得,
F1===80N,B正确;
C.
由A分析知,动力臂为0.5m,阻力臂为0.4m,动力臂大于阻力臂,动力小于阻力,为省力杠杆,C错误;
D. F1的方向从图示位置转到虚线所示的位置的过程中,动力臂变大,F1逐渐变小,D错误。
故选B.
5.C
【解析】
【详解】
设拉力的力臂为l,
根据杠杆的平衡条件F1l1=F2l2可知,
当杠杆在水平位置平衡时:Fl=GlOD,
则拉力F=,
因为G,lOD不变,lOD=l=r,所以F=G,
由于F1、F2、F3的力臂都是圆的半径,故F1=
F2=
F3=G.
故C正确.
6.A
【解析】
【详解】
把木板看做一根杠杆,抬起一端,则另一端为支点;两次抬起木板时的情况如图所示(第一次动力臂较小):
两种情况下,动力克服的都是木板的重力,对于形状规则质地均匀的物体,其重心都在其几何中心上,所以阻力臂都等于动力臂的二分之一,都是省力杠杆,故CD错误A正确;
根据杠杆的平衡条件可得F=GL阻L动=G,所以前后两次所用的力相同,故B错误。
7.D
【解析】
如图所示,G表示杆AB的自重,LOA表示杆的重心到A端的距离,T表示悬线拉力的大小,L表示作用于杆AB上的悬线拉力对A点的力臂.
把AB视为一根可绕A端转动的杠杆,则由杠杆的平衡条件应有:,
由此得:当线套在杆上逐渐向右移动时,拉力T的动力L(L1、L2、L3、L4)经历了先逐渐变大后又逐渐变小的过程,故悬线的拉力T则是逐渐变小后逐渐变大.故D正确,ABC错误.
故选:D.
【点睛】本题考查力矩平衡条件,当阻力和阻力臂的乘积一定时,分析省力情况就要看动力臂的大小变化,所以本题画出图中动力臂是解决本题的关键。
8.A
【详解】
①物块C向右移动时,水平方向上受向右的推力,水平面向左的摩擦力和AB对C向左的摩擦力,因为物体间力的作用是相互的,所以C对木板AB的摩擦力是向右的,故①正确;
②木板AB在竖直方向上受重力和物块C对它的支持力的作用,在水平方向上受木块C对它向右的摩擦力,故②错误;
③物块C受到的重力、地面对它的支持力以及木板AB对它的压力,所以物块C受到的重力和地面对它的支持力不是一对平衡力,故③错误;
④以杆为研究对象,杆受重力G和C对它的支持力F支,两力臂如图所示:
根据杠杆平衡条件可得:F支 L支=G LG,
水平力F由A向B缓慢匀速推动木块,F支的力臂在减小,重力G及其力臂LG均不变,
所以根据杠杆平衡条件可知,在整个过程中支持力在逐渐增大;
由于支持力逐渐变大,且力的作用是相互的,所以可知杆对物体C的压力也逐渐变大,
根据影响摩擦力大小的因素可知,C和木板间、C和地面间的摩擦力逐渐增大,由力的平衡条件知,水平推力F也逐渐增大,故④正确。
综合分析只有①④正确。
故A符合题意。
9.C
【详解】
以A点为支点,阻力为担架的总重力,阻力作用在O点;由下图可知,方式一:由A为支点,阻力臂为AC,动力臂为AD,由相似三角形的性质可得:
=
根据杠杆平衡条件可得:
F乙 AD=G AC
则
F乙=G=G------①
由上图可知,方式二:由A为支点,根据杠杆平衡条件可得:
F乙′ AB=G AO
则
F乙′=G------②
比较①②两式可知,F乙′=F乙;所以,两种救援方式一样省力,从保护伤员的角度看,应采用“方式二”故选C。
10.D
【详解】
A.物体的质量
m===20kg
故A错误;
B.当外力作用在A端提重物时,由于动力的方向不确定,所以动力臂和阻力臂的大小关系不能确定,自然不一定为省力杠杆,故B错误;
C.若用100N竖直向上的力作用在A端,阻力臂
OC==
动力臂OB=40cm,
由杠杆平衡条件可得
FB×OB=FC×OC
即
100N×40cm=FC×20cm
则杠杆C处受到的拉力:FC=200N,
由于力的作用是相互的,则杠杆对物体向上的拉力也为200N,那么这个拉力正好和物体的重力平衡,所以此时正方体物体不受支持力,只受到重力和拉力2个力的作用,故C错误;
D.要作用在A端的力最小,动力臂应最大,如下图,以OA为动力臂,垂直OA向上施加的力最小,
在直角三角形ABO中
OA==50cm
若使物体对地面的压强为6000Pa,则物体对地面的压力:
F压=pS=6000Pa×=60N
所以杠杆对物体的拉力
F拉=G-F压=200N-60N=140N
由杠杆平衡条件可得
FA×OA=FC×OC
即
FA×50cm=140N×20cm
解得:FA=56N,故D正确。
故选D。
11.B
【详解】
A.根据杠杆的平衡条件知,OA>OB,所以FA
C.如果甲浸没在水中,受到浮力的作用,FA会减小,硬棒会顺时针转动,故C错误;
D.如果甲浸没在水中,受到浮力的作用,FA会减小,lA不变,FB不变,根据杠杆平衡条件得,要使硬棒水平平衡,lB应减小,即可将乙向左移动,故D错误。
故选B。
12.A
【详解】
由图示知道,在力F的方向通过了距离,由W=Fs知道,拉力做了功;杠杆在转动的过程中符合杠杆平衡的条件,即阻力为硬棒的重力,大小不变,硬棒在竖直位置时,重力的力臂为0,转过θ角后,重力力臂(阻力臂)逐渐增大,动力臂变小;由杠杆平衡的条件知道,阻力与阻力臂的乘积增大,而动力臂减小,所以拉力逐渐增大,故A符合题意。
故选A。
13.B
【详解】
A.在B端施加动力使杠杆在水平位置平衡,B点动力的方向不同时,动力臂可能大于或小于或等于阻力臂,所以该杠杆可能省力,可能费力,还可能既不省力也不费力,故A错误;
B.由于动力的方向水平向右时,动力臂为零,而阻力和阻力臂的乘积不为零,所以,杠杆不可能平衡,则动力的方向不可能水平向右,故B正确;
C.阻力是阻碍杠杆转动的力,本题中杠杆所受阻力是重物对杠杆向下的拉力,故C错误;
D.在阻力和阻力臂一定时,若施加动力的方向不同,动力臂也可能相同,根据杠杆平衡条件知道,动力的大小可能相同,故D错误。
故选B。
14.B
【分析】
力臂是从杠杆的支点到力的作用线之间的垂线段的长度;根据杠杆的平衡条件F1L1=F2L2分析即可。
【详解】
如下图所示,
根据杠杆的平衡条件得到
G×L2=F×L1
即
G×OA×cosα=F×OB×sinα
当∠α增大时,cosα变小,而sinα变大;
因此重力和它的力臂乘积变小,故C、D错误;
因为OB×sinα变大,所以动力F的力臂变大,而F却变小,故B正确,A错误。
15.C
【详解】
A.设甲的重力为G,甲的底面积为S,杠杆上1小格为L,则根据杠杆平衡条件可得
F甲×6L=G乙×2L
F甲×6L=15N×2L
解得F甲=5N,此时甲对地面的压强为
p==4000Pa
同理可得
F甲′×6L=15N×3L
解得F甲′=7.5N,此时甲对地面的压强为
p′==3750Pa
两式联立解得G=45N,故A错误;
B.甲的底面积为
S==0.01m2
甲是正立方体,边长为
=0.1m
故其体积为
V甲=(0.1m)3=0.001m3
又因为
G甲∶G乙=ρV甲g∶ρV乙g=V甲∶V乙=45N∶15N=3∶1
故乙的体积为
V乙=×0.001m3≈0.00033m3=330cm3
故B错误;
C.如果将甲向右移动并挂于B正下方,乙仍挂于E,此时
F′×4L=G乙×3L
F′×4L=15N×3L
解得
F'=11.25N<20N
所以放手后杠杆仍能平衡,故C正确;
D.将甲向右移动并挂于C正下方,乙移挂至F,假设杠杆平衡,则
F″×2L=G乙×7L
F″×2L=15N×7L
解得
F''=52.5N>20N
所以放手后细线拉力会大于20N,细线会断,则甲不会被拉离地面,故D错误。
故选C。
16.D
【详解】
分析杠杆的五要素,如如图所示:。
A.设杠杆与竖直方向的夹角为θ,F1的力臂
L1=cosθ×OA
重力的力臂
根据杠杆的平衡条件
因θ变大时,F1也变大,A错误。
B.F2与杠杆垂直,动力臂大小等于OA,保持不变,杠杆的G不变,在上升的过程中,阻力臂变大,根据杠杆的平衡条件,F2逐渐变大,B错误;
C.F3始终沿即沿竖直方向,由图可知,动力臂始终是阻力臂的2倍,根据杠杆的平衡条件,F3始终等于,故C错误。
D.由功的原理,使用任何机械不省功,三次拉力抬升木棒的过程中所做的功均相等,D正确。
故选D。
17.D
【详解】
A.动力F和θ的关系,当从水平→90°→水平,F对应的动力臂,先变小后变大,所以A错误。
B.当θ等于90°时动力最小但不为零,所以B错误。
CD.根据杠杆平衡条件
FL=F2L2
得
则F和L成反比,所以C错误,D正确。
故选D。
18.D
【解析】
【详解】
AB.因无法确定动力臂的大小,所以无法确定它是哪种杠杆,故A和B错误;
CD.加在B点的动力F与OB垂直向上时,动力作用线和杠杆垂直,支点与动力作用点之间的连线OB就是最长的动力臂,此时动力最小。因为C点是中点,所以OB>OA=2OC。
根据杠杆的平衡条件,此时的最小动力:
所以选项C错误,选项D正确。
19.C
【详解】
A.
如图1,支点为,,,
木棒平衡,
,
,
故A正确,不符合题意;
B.
如图2,支点为,,,
木棒平衡,
,
,
故B正确,不符合题意;
C.
如图3,支点为,,,
木棒平衡,
,
,
故C错误,符合题意;
D.
如图4,支点为,,,
木棒平衡,
,
,
故D正确,不符合题意。
20.B
【详解】
铁球的重力
G=mg=12kg×10N/kg=120N
由图知,当力F作用在球的下边缘,且与通过AB的直径垂直时,动力臂最长,其受力图如图所示
把整体看做一个杠杆,支点在B点,由图知,球的重力方向竖直向下,力臂为LG,由图知
LG=R
F的力臂等于杆的长度与球的直径之和,则
根据杠杆的平衡条件得
G LG=F LF
代入数据
解得
F=45N
故选B。
21.D
【分析】
A.已知物体的重力和体积,根据公式ρC=求物体C的密度。
B.利用阿基米德原理求受到的浮力,再根据杠杆A端受到的拉力等于C的重力减去浮力计算即可。
C.利用杠杆平衡条件F1L1=F2L2求杠杆B端受到细线的拉力,由于力的作用是相互的,可求杠杆B端对D的拉力,D对地面的压力等于D的重力减去拉力,利用压强公式计算D对地面的压强。
D.物体C浸没在水中前后,水的深度变化等于排开水的体积除以底面积,再利用p=ρgh求水对容器底的压强增大值。
【详解】
A.物体C的密度
ρC===8×103kg/m3
故A正确不合题意。
B.物体受到的浮力
F浮=ρ水gV排=1×103kg/m3×10N/kg×1×10-3m3=10N
杠杆A端受到的拉力
FA=GC-F浮=80N-10N=70N
故B正确不合题意。
C.由杠杆平衡条件F1L1=F2L2得
FA×OA=FB×OB
70N×2=FB×1
解得
FB=140N
由于力的作用是相互的,杠杆B端对D的拉力
F拉=FB=140N
对地面的压力
F压=GD-FB=mDg-F拉=20kg×10N/kg-140N=60N,
对地面的压强
p===1.5×103Pa
故C正确不合题意。
D.物体C浸没在水中前后,水的深度变化
h====2.5cm=0.025m
水对容器底的压强增大值
p=ρ水g h=1×103kg/m3×10N/kg×0.025m=2.5×102Pa
故D错误符合题意。
故选D。
22.C
【详解】
A.由于拉力始终竖直向上,由杠杆的平衡条件可知,拉力不变(动力臂与阻力臂之比不变)。
由图乙可知,当B端离地1.2m时,A端刚离地,所以金属棒长1.2米,故A错误;
BC.因为
W=Gh
所以金属棒的重力
即
F2=5N
杆未离地前,动力臂与阻力臂的比值不变,拉力大小不变,
由图乙可知拉力
故B错误、C正确。
D.由杠杆平衡条件得重心到A端的距离
故D错误。
故选C。
23.30;
不变
【分析】
杠杆静止不动或匀速转动都叫做杠杆平衡,本题应用杠杆的平衡条件来求解,关键是找到动力臂和阻力臂,在OA位置很容易看出:OA为动力臂,G对杠杆的向下拉力F2=G对应的力臂为1/2
OA,据动力×动力臂=阻力×阻力臂。
【详解】
由于重物悬挂在杠杆AO的中点上,所以力F的力臂LF是重力G的力臂LG的2倍,即LF=2LG.根据杠杆的平衡条件得,F==30
N.在杠杆由A到B的过程中,重力的大小和方向都没有变化,而两个力臂都发生了变化.但是在变化的过程中两个力臂之间始终保持着LF=2LG的关系,所以力F将保持不变。
【点睛】
分析本题杠杆的动态平衡时,应该动中取静,根据杠杆平衡条件,分析比较,得出结论。
24.150
75000
【详解】
(1)[1]根据杠杆的平衡条件得到
G×OA=F×OB
F==150N
(2)[2]最小力抬住引擎盖时双手受到的压强
=75000Pa
25.0.8
下
【详解】
(1)[1]容器的质量为m1,钩码的质量为m2,容器中液体的质量为m,根据杠杆的平衡条件得
G总×OC
=G砝码×OD
(m1+m)g×OC=m2g×OD
则液体的密度
(2)[2]若让砝码位置不变即质量不变,根据
可知:体积小的密度大,所以下边的刻度对应的数值大。
26.C
200
靠近
【详解】
[1]三角支架ABC可看作杠杆,C点是支点,如果A处螺钉松脱,则支架会绕C点倾翻;
[2]空调受到重力而作用在支架上的压力是阻力,这个压力大小等于空调机的重力大小,阻力臂为AB,动力臂为AC,根据杠杆的平衡条件,
A处螺钉的水平拉力为
;
[3]由杠杆的平衡条件
FA×AC=G×L阻
室外机对支架的作用力大小等于重力,是一定的,AC也是定值,为了安全,即应减小处螺钉的水平拉力FA的大小,应减小L阻大小,故室外机的位置应尽量靠近墙壁。
27.10
10
0.8m
1m
【分析】
(1)物体匀速直线运动时处于平衡状态,水平方向受到的两个力为平衡力,根据二力平衡条件求出滑块匀速运动时所受的摩擦力的大小。
(2)根据求出当滑块匀速运动时拉力F做功的功率。
(3)当M在O点左侧且绳子的拉力为0时,根据杠杆的平衡条件得出滑块水平平衡的最左侧位置;当在O点右侧且拉力为60N时,根据杠杆的平衡条件得出滑块在O点最右侧的位置,即可得出滑块移动的范围,要注意均匀杠杆的重心位于几何中心上。
【详解】
(1)[1]滑块匀速运动时处于平衡状态,水平方向的拉力和受到的摩擦力是一对平衡力,则根据二力平衡条件可知
(2)[2]当滑块匀速运动时拉力F做功的功率
(3)[3]设AB的中点为C,当M在O点左侧离O点米,绳子的拉力T=0时,如下图所示:
根据杠杆平衡条件则有
解得:;
[4]当M在O点右侧离O点米时,绳子的拉力T=60N,如下图所示:
根据杠杆平衡条件则有
解得:;
故滑块在O点左侧0.8m到右侧1m范围内滑动才能使AB保持水平。
28.32.5
小于
【详解】
(1)[1]在阻力与阻力臂一定的情况下,动力臂越大,动力越小,由图示可知,AD是最大动力臂,过A与AD的垂直的力最小,如图所示
由几何知识可得
在推翻油桶过程中,小明至少需要对油桶做功
(2)[2]由图甲与图乙所示可知,两种情况下,最小推力的动力臂相等,两种情况下阻力相等,图甲的阻力臂小于图乙的阻力臂,由杠杆平衡条件可知,图甲中的推力小于图乙中的推力,即F1小于F2。
29.24
16
【详解】
[1]物体AB压在两托盘秤上,则两托盘秤的示数之和为物体的重力
G=6N+18N=24N
[2]以B为支点,设物体AB长度为L1,重力对应力臂为L2根据杠杆平衡条件,则开始时有
F甲L1=GL2①
当让C点放在托盘秤甲的小木块上后,甲托盘秤向上的支持力的力臂变为,重力力臂不变,则根据杠杆平衡条件有
②
有①②综合可得
得
则乙托盘秤示数为
30.3.5×103kg/m3
【详解】
用细绳把金属块悬挂于A点,用弹簧秤在B点施加一个竖直向上的力,当OB杠杆水平静止时,弹簧秤读数为2.1N,则根据杠杆平衡条件知道
F1 OB=FG OA
则
由于金属块受重力和拉力而处于平衡状态,所以,此金属块的重力
G=FG=6.3N
浸没水中后由杠杆平衡条件知道,
则
金属块此时受重力G、浮力F浮及拉力F′而处于平衡状态,即
G=F浮+F′
则金属块受到的浮力
F浮=G-F′=6.3N-4.5N=1.8N
由F浮=ρgV排知道,排开水的体积
由
知道,金属块的质量
由知道,金属块的密度
31.2
3∶1
【详解】
(1)[1]杠杆水平平衡时a物体受到两个力作用,分别是a的重力和绳子对a的拉力。
(2)[2]由图可知,以B为支点,根据杠杆平衡条件可得
Ga×AB=Gb×BD
由
AB=CD=BC
可得
2AB=BC,BD=3AB
Gb=
平台台面BC受到的最小压力
F小=Ga+Gb=9N+3N=12N
以C为支点,根据杠杆平衡条件可得
Ga×AC=Gb′×CD
由
AB=CD=BC
可得
2CD=BC,AC=3CD
平台台面BC受到的最大压力
F大=Ga+Gb=9N+27N=36N
32.始终不变
0.875
1
【详解】
(1)[1]用力F推直棒,直至有长度露出桌面外,压力和接触面的粗糙程度不变,摩擦力大小不变。
(2)[2]小球运动到D点时,直棒会顺时针翻转,如图所示:
OC的长度为
OC=1m×-1m×m=0.25m
OD的长度为
OD=1m×-(1m-vt)=1m/s×t-0.75m
由杠杆平衡条件得到
G×OC=F×OD
4N×0.25m=8N×(1m/s×t-0.75m)
t=0.875s
(3)[3]如图所示:
在B端将直棒以最小力逆时针抬起30°,至少对直棒做功等于克服重力做的功
W=Gh=G××AB=4N×××1m=1J
33.(1)F1L1=F2L2;(2)见解析
【详解】
解:(1)杠杆平衡的条件
F1L1=F2L2
(2)设被测物体的密度为ρ物,体积为V,挂物体处离提的距离为L0,秤锤重为G0,根据杠杆的平衡条件可得,空气中
ρ物VgL0=G0Ll------①
浸没在中后
(ρ物Vg-ρVg)L0=G0L2------②
由①、②两式解得
ρ物=
答:(1)杠杆平衡的条件F1L1=F2L2;
(2)被测物体的密度ρ物=。
34.降低
减小
2000W
1.5m
【详解】
(1)[1][2]高压气瓶向气垫内充气时,气体膨胀对外做功,内能减小,温度降低。
(2)[3]高压起重气垫做功
W=Gh=105N×0.1m=10000J
功率为
P===2000W
(3)[4]将石板当做杠杆如图:
气垫对石板的压力
F=pS=106Pa×400×10 4m2=40000N
质地均匀的长方体石板,所以,重心在中心,根据杠杆的平衡条件得到
F×OA=G×l2
气垫的中心离石板右端的距离
OA===1.5m
35.10
2×103kg/m3
见解析
【详解】
(1)[1]当小桶为空桶时移动秤砣至某点,设该点为E,此时密度秤正好水平平衡,小桶的质量为0.2kg,秤砣的质量为0.2kg,左侧的力臂为AO=10cm,则杠杆平衡条件F1l1=F2l2得
G桶OA=G砣OE
m桶gOA=m砣gOE
OE==10cm
即密度秤零刻度在O点右侧10cm处。
(2)[2]当右侧的力臂为
OB=AB-OA=40cm-10cm=30cm
时,该密度秤小桶所能测量液体的质量最大,则密度就最大,根据杠杆平衡条件得
(G桶+G液体)OA=G砣OB
(m桶+m液)gOA=m砣gOB
液体的质量
m液=×0.2kg-0.2kg=0.4kg=400g
液体的最大密度
ρ液最大=
(3)[3]液体的密度
由此可知:液体密度与提钮到秤舵的距离之间的关系是一次函数,因此密度秤的刻度是均匀的。
36.1.25×104Pa
100N
500N
不变
【详解】
(1)[1]对秤的压力为
F=G=mg=50kg×10N/kg=500N
对秤的压强为
p===1.25×104Pa
(2)[2]由题意知,体重计的示数变化为
m=60kg 50kg=10kg
根据力的作用的相互性可知,对B的提力
F=mg=10kg×10N/kg=100N。
(3)[3]根据杠杆的平衡条件可得
G×OA=F×OB
则
G===500N。
(4)[4]如果该同学用双手竖直向上匀速抬起木棒,物体的重力不变,动力臂和阻力臂的比值也不变,所以力F不变,则体重计显示的读数将不变。
37.m2∶m1
仍然平衡
见解析
【详解】
(1)[1]由杠杆平衡公式可得
则
l1∶l2=m2∶m1
(2)[2][3]浸入水中之后左边向下拉力
浸入水中之后右边向下拉力
则动力与动力臂乘积为
①
阻力与阻力臂乘积为
②
又由
得
则
故代入①②可得
杠杆依然保持平衡。
答案第1页,共2页
答案第1页,共2页
同课章节目录
- 第1章 物质及其变化
- 第1节 物质的变化
- 第2节 物质的酸碱性
- 第3节 常见的酸
- 第4节 常见的碱
- 第5节 酸和碱之间发生的反应
- 第6节 几种重要的盐
- 第2章 物质转化与材料利用
- 第1节 金属材料
- 第2节 金属的化学性质
- 第3节 有机物和有机合成材料
- 第4节 物质的分类
- 第5节 物质的转化
- 第6节 材料的利用与发展
- 第3章 能量的转化与守恒
- 第1节 能量及其形式
- 第2节 机械能
- 第3节 能量转化的量度
- 第4节 简单机械
- 第5节 物体的内能
- 第6节 电能
- 第7节 核能
- 第8节 能量的转化与守恒
- 第4章 代谢与平衡
- 第1节 食物与营养
- 第2节 食物的消化与吸收
- 第3节 体内物质的运输
- 第4节 能量的获得
- 第5节 体内物质的动态平衡
- 研究性学习课题
- 一 当地酸雨情况以及对农作物和建筑物的影响
- 二 金属对社会发展的作用
- 三 寻找自行车中的杠杆
- 四 怎样防治龋齿
