3.2.2函数的最大(小)值 课件(共17张PPT)
文档属性
| 名称 | 3.2.2函数的最大(小)值 课件(共17张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-08 11:42:07 | ||
图片预览






文档简介
(共17张PPT)
3.2.2函数的最大(小)值
人教A(2019)版
必修一
新知导入
增函数
减函数
定义
一般地,设函数f(x)的定义域为I.如果对于定义域I内某个区间D上的任意两个自变量x1,x2.
当x1当x1f(x2),那么就说函数f(x)在区间D上是减函数
图象
描述
自左向右看图象是上升的
自左向右看图象是下降的
复习巩固
一、单调性定义
新知导入
二、根据函数的单调性的定义,证明(判定)函数f(x)在其区间上的单调性的步骤:
(1)设x1、x2是该区间上的任意两个值,且x1<x2;
(2)作差f(x1)-f(x2),然后变形;
(3)判定f(x1)-f(x2)的符号;
三、一次函数、二次函数等基本初等函数的单调性及单调区间
四、复合函数的单调性
对于复合函数y=f[g(x)],若t=g(x)在区间(a,b)上是单调函数,且y=f(t)在区间(g(a),g(b))或者(g(b),
g(a))上是单调函数,若t=g(x)与y=f(t)的单调性相同
(同时为增或减),则y=f[g(x)]为增函数;若t=g(x)与y=f(t)的单调性相反,则y=f[g(x)]为减函数.简称为:同增异减.
新知讲解
五、(1)函数y=-f(x)与函数y=f(x)的单调性相反;
(2)当f(x)恒为正或恒为负时,函数
与y=f(x)的单调性相反;
(3)在公共区间内,增函数+增函数=增函数,增函数-减函数=增函数等;
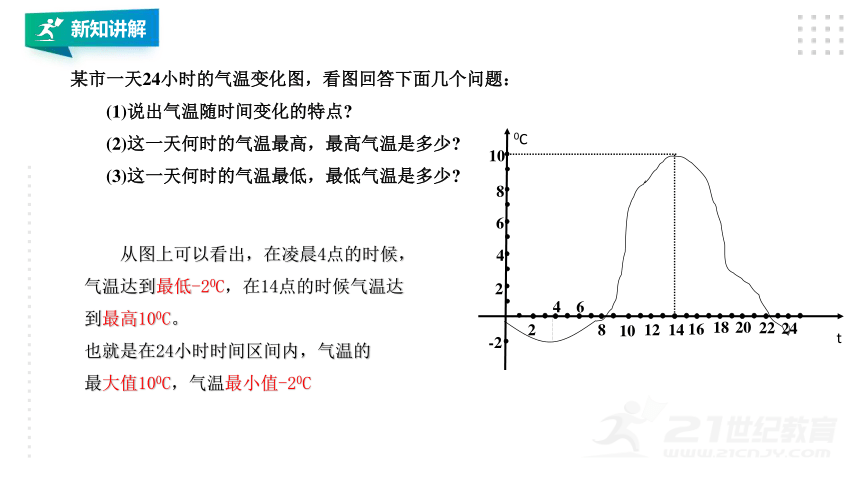
某市一天24小时的气温变化图,看图回答下面几个问题:
(1)说出气温随时间变化的特点
(2)这一天何时的气温最高,最高气温是多少
(3)这一天何时的气温最低,最低气温是多少
2
4
6
8
10
12
14
24
16
18
20
22
2
4
6
8
10
-2
新知讲解
t
0C
从图上可以看出,在凌晨4点的时候,
气温达到最低-20C,在14点的时候气温达
到最高100C。
也就是在24小时时间区间内,气温的
最大值100C,气温最小值-20C
新知讲解
函数的最大值最小值概念
一般地,设函数
y
=
f
(x)
的定义域为I,如果存在实数
M
满足:
(1)
对于任意的
x∈I,都有
f
(x)≤M,
(2)
存在
x0
∈I,使得
f
(x0)
=M,
那么称M是
y
=f
(x)
的最大值,记为
1、函数的最大值
我们类比最大值定义,给出最小值定义
2、函数的最小值
一般地,设函数
y
=
f
(x)
的定义域为I,如果存在实数M
满足:
(1)
对于任意的x∈I,都有
f
(x)
≥M,
那么称M是
y
=
f
(x)
的最小值,记为
(2)
存在
x0
∈I,使得f
(x0)
=M,
新知讲解
特别地,定义在闭区间上的单调函数必有最大(小)值.设f(x)是定义在[m,n]上的单调增函
数,则它的最大值是f(n),最小值是f(m);单调减函数正好相反。
例4
“菊花”烟花是最壮观的烟花之一,制造时一般是期望在它达到最高点时爆裂.(大
约是在距地面高度18cm的地方点火,并且烟花冲出的速度是14.7m/s)
(1)写出烟花距地面的高度与时间之间的关系式
(2)烟花冲出后什么时候是它爆裂的最佳时刻?这时距地面的高度是多少(精确到1m)?
解:
(1)
设烟花在
t
s时据地面的高度为h
m,则由物理运动原理可:
(2)作出函数
的图象
h
t
由二次函数图像和性质知:
于是,烟花冲出后1.5s是它爆裂的最佳时刻,这时距地面的高度约为29m
函数求值域的方法
一、图像法
合作探究
例2
求函数
在区间[2,6]上的最大值和最小值.
2
6
2
0
所以,函数
在区间
[2,6]上单调递减.
因此,函数
在区间
[2,6]的两个端点上分别取得最大值与最小
值.
在
x=2时取得最大值,最大值是2;在x=6时取得最小值,最小值是0.4
二、单调性法
合作探究
合作探究
三、配方法
配方法是求二次函数最值最基本的方法之一。
1.求函数
的值域。
解:
所以,当x=1时,y取最小值4;当x=-1时,y取最大值8。
1、求函数
最大值。
四、换元法
将复杂的复合函数通过换元转化成常见的基础函数。
解:令,则x=1-t2,t≥0,那么原式可化为:y=2(1-t2)+4t=-2t2+4t+2,t≥0
y=-2(t-1)2+3,t≥0,当t=1时,y取最大值3
五、基本不等式法
1.已知
0,求函数
y=x-x2
的最大值
解:y=x-x2=x(1-x),由00,1-x>0,满足基本不等式条件,
所以,y=x(1-x)≤
课堂练习
1、已知函数f(x)=-x2+4x+a,x∈[0,1],若f(x)有最小值-2,求f(x)的最大值
解:因为函数f(x)=-x2+4x+a在x∈(-∞,2]上单调递增,所以在x∈[0,1]上单调递增,
所以,当x=0时,f(x)取最小值f(0)=a=-2,故a=-2
因此,f(x)=-x2+4x-2,x∈[0,1],又因为在x∈[0,1]上单调递增,所以
f(x)的最大值为f(1)=1
2、已知函数f(x)=
(x∈[1,+∞)).求f(x)的最小值.
解:由f(x)==+2,当且仅当x=时取等号。
所以f(x)的最小值为+2
课堂练习
3、求函数f(x)=+x的最小值。
4.函数f(x)=
求f(x)的最大值、最小值。
解:因为y=y=x均为增函数,故f(x)在定义域[
所以f(x)的最小值为f()=
解一:画出f(x)图像,如图:当x=-1时,取最小值6
-1
1
2
6
8
10
当x=2时,取最大值10
解二:当x
当x
所以,f(x)最大值10,最小值6
课堂总结
函数的最大值最小值概念
1、函数的最大值
(1)
对于任意的
x∈I,都有
f
(x)≤M,
(2)
存在
x0
∈I,使得
f
(x0)
=M,
2、函数的最小值
(1)
对于任意的x∈I,都有
f
(x)
≥M,
(2)
存在
x0
∈I,使得f
(x0)
=M,
求最大值最小值的方法
一、图像法
二、单调性法
三、配方法
四、换元法
五、基本不等式法
板书设计
前提
设函数y=f(x)的定义域为I,如果存在实数M满足
条件
①对于任意x∈I,都有___________;
②存在x0∈I,使得
_____________.
①对于任意x∈I,都有____________;
②存在x0∈I,使得
_______________.
结论
M为最大值
M为最小值
f(x)≤M
f(x)≥M
f(x0)=M
f(x0)=M
注意:在最值中,特别注意存在存在x0∈I,
f(x0)=M
一、最值定义
二、最值的求法
一、图像法
二、单调性法
三、配方法
四、换元法
五、基本不等式法
作业布置
1.已知函数,求f(x)的最大、最小值.
2.课本P86页,4、7、10
https://www.21cnjy.com/help/help_extract.php
3.2.2函数的最大(小)值
人教A(2019)版
必修一
新知导入
增函数
减函数
定义
一般地,设函数f(x)的定义域为I.如果对于定义域I内某个区间D上的任意两个自变量x1,x2.
当x1
图象
描述
自左向右看图象是上升的
自左向右看图象是下降的
复习巩固
一、单调性定义
新知导入
二、根据函数的单调性的定义,证明(判定)函数f(x)在其区间上的单调性的步骤:
(1)设x1、x2是该区间上的任意两个值,且x1<x2;
(2)作差f(x1)-f(x2),然后变形;
(3)判定f(x1)-f(x2)的符号;
三、一次函数、二次函数等基本初等函数的单调性及单调区间
四、复合函数的单调性
对于复合函数y=f[g(x)],若t=g(x)在区间(a,b)上是单调函数,且y=f(t)在区间(g(a),g(b))或者(g(b),
g(a))上是单调函数,若t=g(x)与y=f(t)的单调性相同
(同时为增或减),则y=f[g(x)]为增函数;若t=g(x)与y=f(t)的单调性相反,则y=f[g(x)]为减函数.简称为:同增异减.
新知讲解
五、(1)函数y=-f(x)与函数y=f(x)的单调性相反;
(2)当f(x)恒为正或恒为负时,函数
与y=f(x)的单调性相反;
(3)在公共区间内,增函数+增函数=增函数,增函数-减函数=增函数等;
某市一天24小时的气温变化图,看图回答下面几个问题:
(1)说出气温随时间变化的特点
(2)这一天何时的气温最高,最高气温是多少
(3)这一天何时的气温最低,最低气温是多少
2
4
6
8
10
12
14
24
16
18
20
22
2
4
6
8
10
-2
新知讲解
t
0C
从图上可以看出,在凌晨4点的时候,
气温达到最低-20C,在14点的时候气温达
到最高100C。
也就是在24小时时间区间内,气温的
最大值100C,气温最小值-20C
新知讲解
函数的最大值最小值概念
一般地,设函数
y
=
f
(x)
的定义域为I,如果存在实数
M
满足:
(1)
对于任意的
x∈I,都有
f
(x)≤M,
(2)
存在
x0
∈I,使得
f
(x0)
=M,
那么称M是
y
=f
(x)
的最大值,记为
1、函数的最大值
我们类比最大值定义,给出最小值定义
2、函数的最小值
一般地,设函数
y
=
f
(x)
的定义域为I,如果存在实数M
满足:
(1)
对于任意的x∈I,都有
f
(x)
≥M,
那么称M是
y
=
f
(x)
的最小值,记为
(2)
存在
x0
∈I,使得f
(x0)
=M,
新知讲解
特别地,定义在闭区间上的单调函数必有最大(小)值.设f(x)是定义在[m,n]上的单调增函
数,则它的最大值是f(n),最小值是f(m);单调减函数正好相反。
例4
“菊花”烟花是最壮观的烟花之一,制造时一般是期望在它达到最高点时爆裂.(大
约是在距地面高度18cm的地方点火,并且烟花冲出的速度是14.7m/s)
(1)写出烟花距地面的高度与时间之间的关系式
(2)烟花冲出后什么时候是它爆裂的最佳时刻?这时距地面的高度是多少(精确到1m)?
解:
(1)
设烟花在
t
s时据地面的高度为h
m,则由物理运动原理可:
(2)作出函数
的图象
h
t
由二次函数图像和性质知:
于是,烟花冲出后1.5s是它爆裂的最佳时刻,这时距地面的高度约为29m
函数求值域的方法
一、图像法
合作探究
例2
求函数
在区间[2,6]上的最大值和最小值.
2
6
2
0
所以,函数
在区间
[2,6]上单调递减.
因此,函数
在区间
[2,6]的两个端点上分别取得最大值与最小
值.
在
x=2时取得最大值,最大值是2;在x=6时取得最小值,最小值是0.4
二、单调性法
合作探究
合作探究
三、配方法
配方法是求二次函数最值最基本的方法之一。
1.求函数
的值域。
解:
所以,当x=1时,y取最小值4;当x=-1时,y取最大值8。
1、求函数
最大值。
四、换元法
将复杂的复合函数通过换元转化成常见的基础函数。
解:令,则x=1-t2,t≥0,那么原式可化为:y=2(1-t2)+4t=-2t2+4t+2,t≥0
y=-2(t-1)2+3,t≥0,当t=1时,y取最大值3
五、基本不等式法
1.已知
0
y=x-x2
的最大值
解:y=x-x2=x(1-x),由0
所以,y=x(1-x)≤
课堂练习
1、已知函数f(x)=-x2+4x+a,x∈[0,1],若f(x)有最小值-2,求f(x)的最大值
解:因为函数f(x)=-x2+4x+a在x∈(-∞,2]上单调递增,所以在x∈[0,1]上单调递增,
所以,当x=0时,f(x)取最小值f(0)=a=-2,故a=-2
因此,f(x)=-x2+4x-2,x∈[0,1],又因为在x∈[0,1]上单调递增,所以
f(x)的最大值为f(1)=1
2、已知函数f(x)=
(x∈[1,+∞)).求f(x)的最小值.
解:由f(x)==+2,当且仅当x=时取等号。
所以f(x)的最小值为+2
课堂练习
3、求函数f(x)=+x的最小值。
4.函数f(x)=
求f(x)的最大值、最小值。
解:因为y=y=x均为增函数,故f(x)在定义域[
所以f(x)的最小值为f()=
解一:画出f(x)图像,如图:当x=-1时,取最小值6
-1
1
2
6
8
10
当x=2时,取最大值10
解二:当x
当x
所以,f(x)最大值10,最小值6
课堂总结
函数的最大值最小值概念
1、函数的最大值
(1)
对于任意的
x∈I,都有
f
(x)≤M,
(2)
存在
x0
∈I,使得
f
(x0)
=M,
2、函数的最小值
(1)
对于任意的x∈I,都有
f
(x)
≥M,
(2)
存在
x0
∈I,使得f
(x0)
=M,
求最大值最小值的方法
一、图像法
二、单调性法
三、配方法
四、换元法
五、基本不等式法
板书设计
前提
设函数y=f(x)的定义域为I,如果存在实数M满足
条件
①对于任意x∈I,都有___________;
②存在x0∈I,使得
_____________.
①对于任意x∈I,都有____________;
②存在x0∈I,使得
_______________.
结论
M为最大值
M为最小值
f(x)≤M
f(x)≥M
f(x0)=M
f(x0)=M
注意:在最值中,特别注意存在存在x0∈I,
f(x0)=M
一、最值定义
二、最值的求法
一、图像法
二、单调性法
三、配方法
四、换元法
五、基本不等式法
作业布置
1.已知函数,求f(x)的最大、最小值.
2.课本P86页,4、7、10
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
