1.3.1函数的单调性与最大最小值
文档属性
| 名称 | 1.3.1函数的单调性与最大最小值 |  | |
| 格式 | zip | ||
| 文件大小 | 625.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-07-31 20:42:18 | ||
图片预览



文档简介
(共43张PPT)
x
y
0
2
2
-2
-2
课题导入
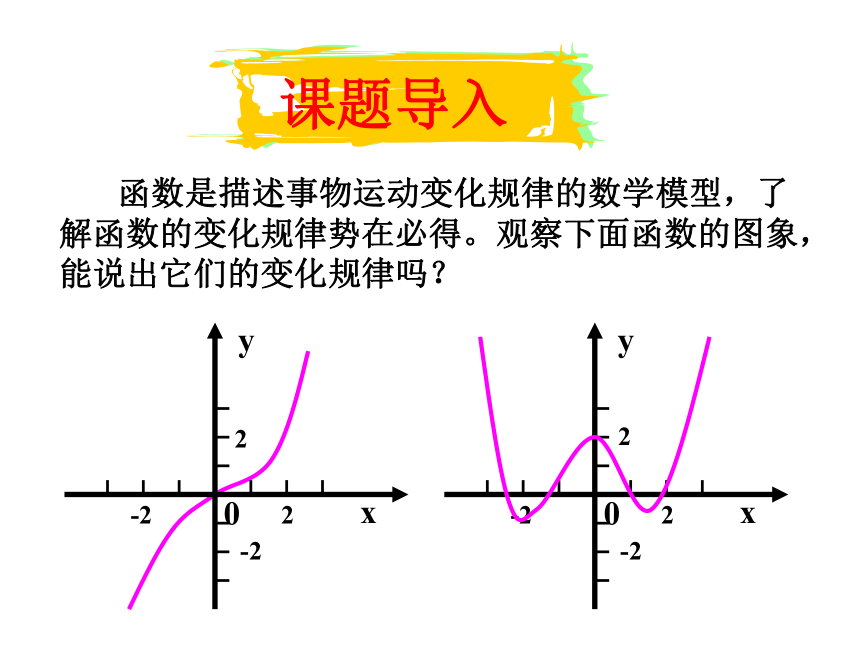
函数是描述事物运动变化规律的数学模型,了解函数的变化规律势在必得。观察下面函数的图象,能说出它们的变化规律吗?
x
y
0
2
-2
2
-2
x
y
0
2
2
-2
-2
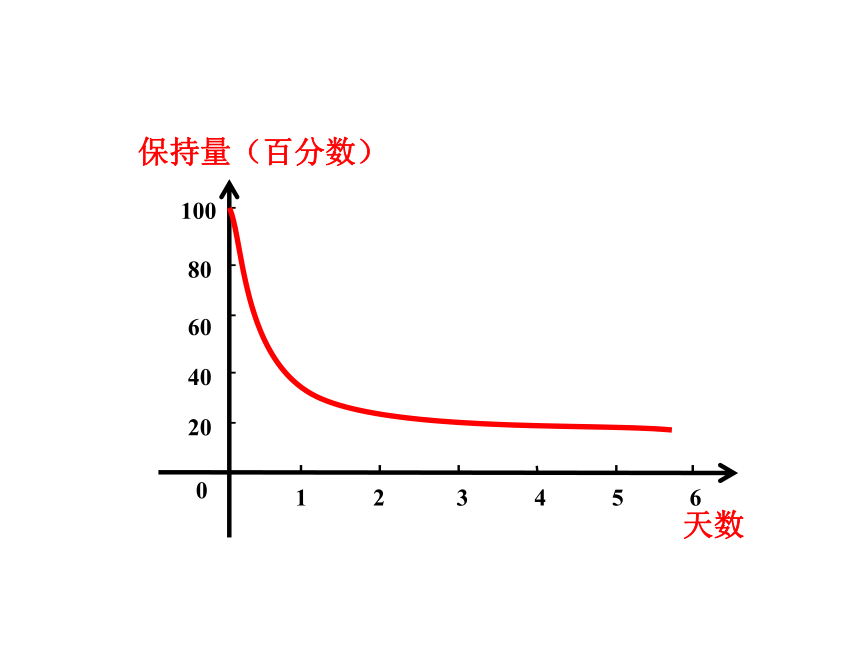
保持量(百分数)
天数
1 2 3 4 5 6
0
20
40
60
80
100
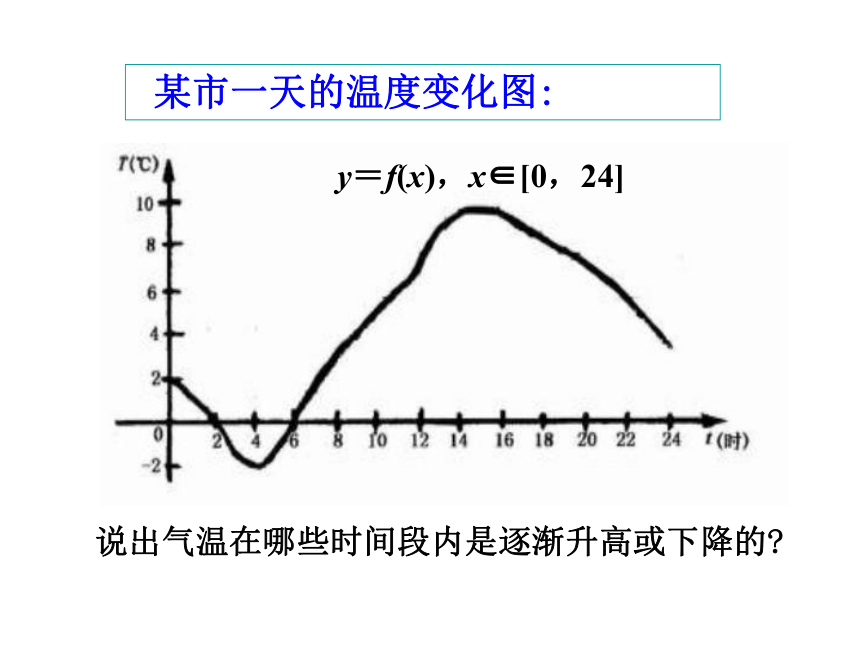
某市一天的温度变化图:
y=f(x),x∈[0,24]
说出气温在哪些时间段内是逐渐升高或下降的
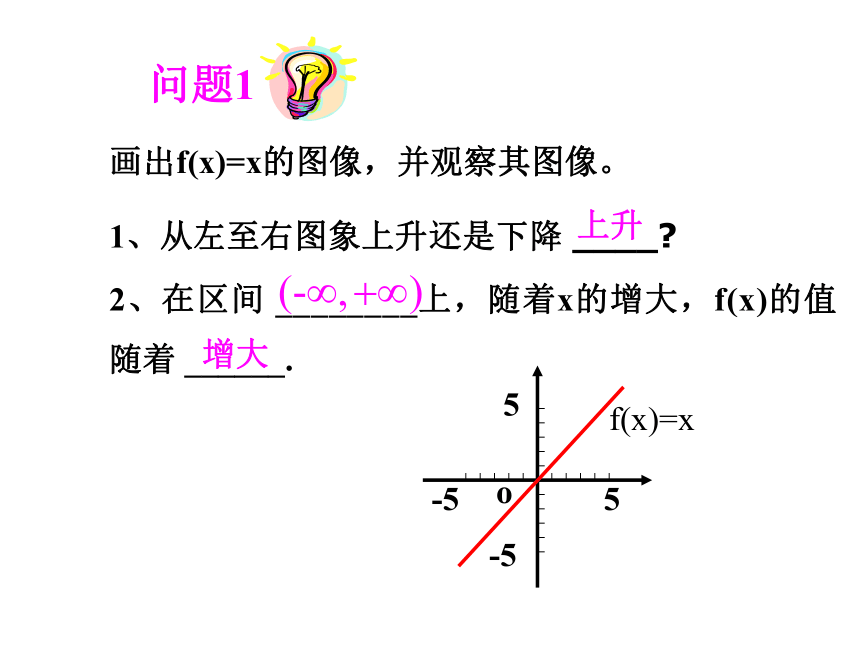
问题1
画出f(x)=x的图像,并观察其图像。
2、在区间 ________上,随着x的增大,f(x)的值随着 ______.
o
5
-5
-5
5
f(x)=x
1、从左至右图象上升还是下降 ____
上升
增大
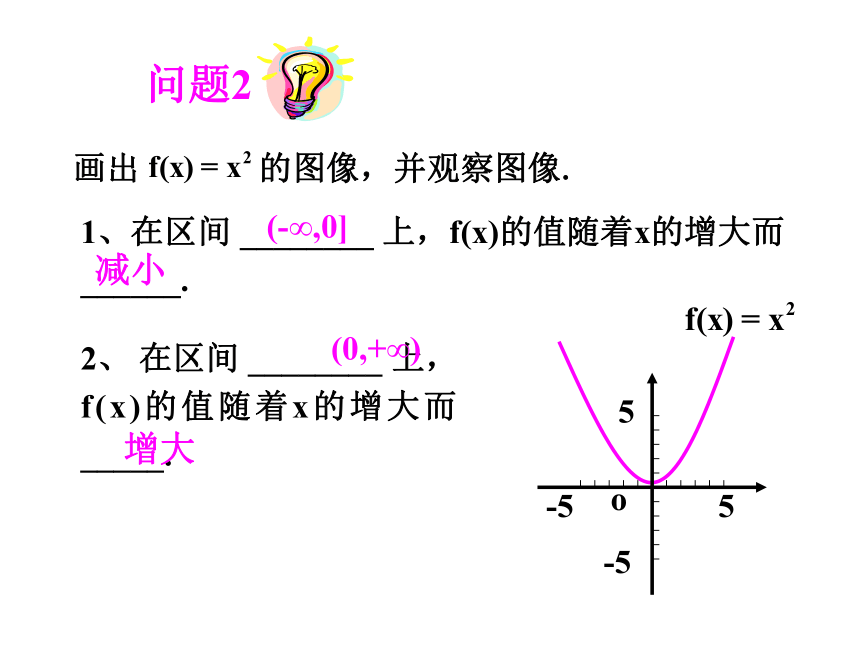
1、在区间 ________ 上,f(x)的值随着x的增大而 ______.
问题2
画出 的图像,并观察图像.
o
5
-5
-5
5
2、 在区间 ________ 上,f(x)的值随着x的增大而 _____.
(-∞,0]
(0,+∞)
减小
增大
对于二次函数 ,我们可以这样描述“在区间 上,随x的增大,相应的f(x)也随着增大”.
在区间 上,任取两个 ,得到
,当
时,有
这时,我们就说函数 在区间 上是这增函数.
x
y
2
1
0
1
3
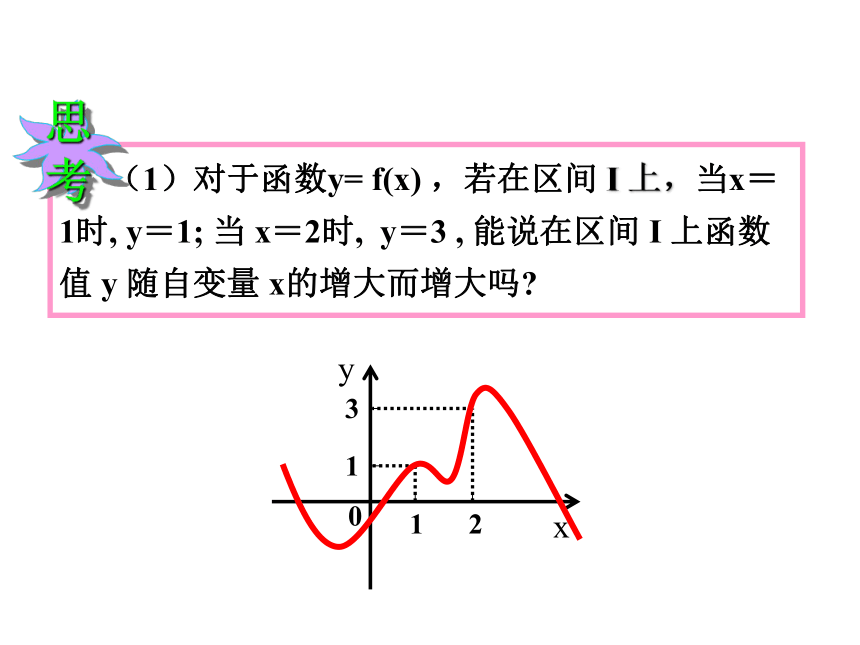
(1)对于函数y= f(x) ,若在区间 I 上,当x=1时, y=1; 当 x=2时, y=3 , 能说在区间 I 上函数值 y 随自变量 x的增大而增大吗
思考
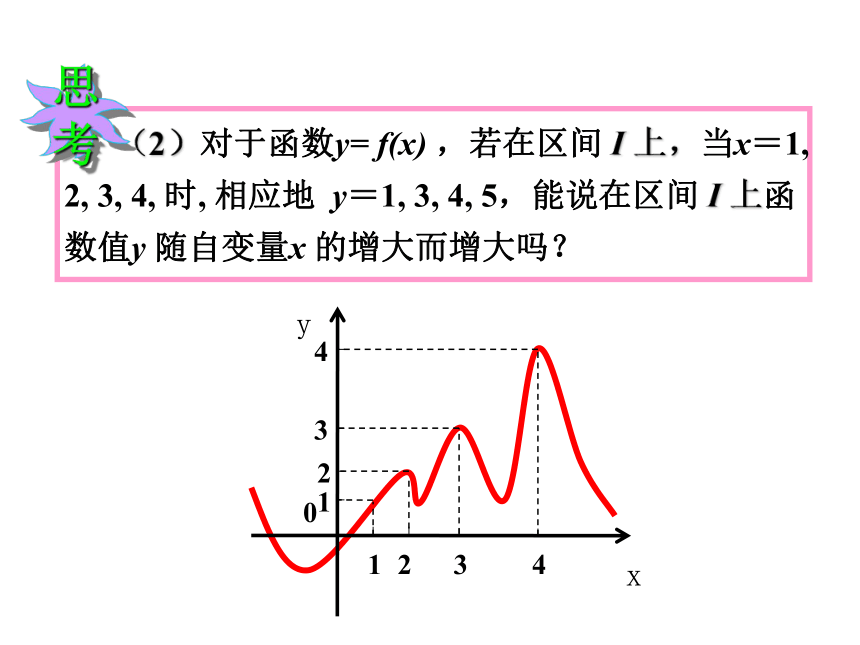
(2)对于函数y= f(x) ,若在区间 I 上,当x=1, 2, 3, 4, 时, 相应地 y=1, 3, 4, 5,能说在区间 I 上函数值y 随自变量x 的增大而增大吗?
思考
x
y
1
0
3
4
2
1
2
3
4
x
y
x1
0
x2
x3
xn
y1
y2
y3
yn
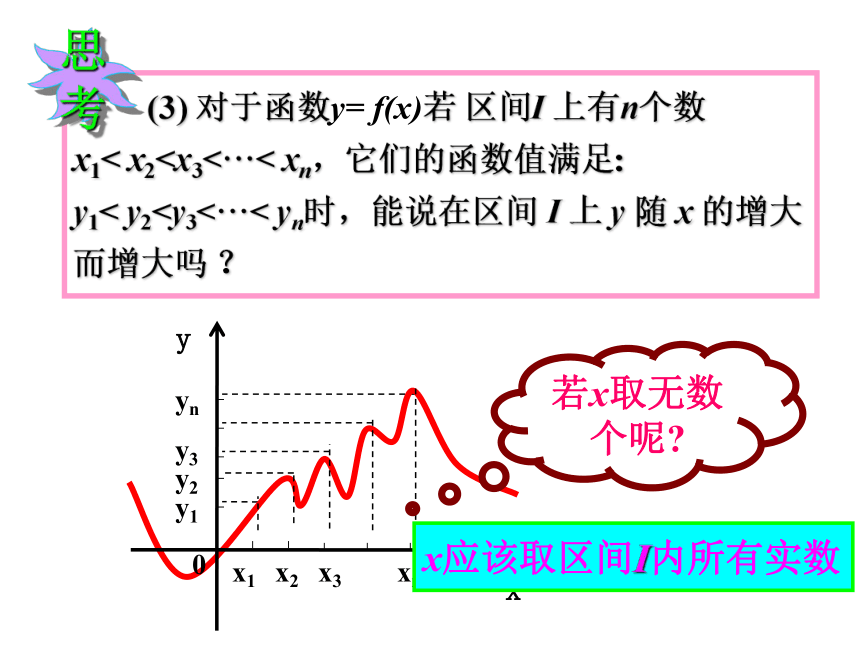
x应该取区间I内所有实数
(3) 对于函数y= f(x)若 区间I 上有n个数
x1< x2y1< y2思考
若x取无数个呢
能否仿照前面的描述,说明函数
在区间(-∞,0]上是减函数吗?
在区间(-∞,0] 上,任取两个 ,得到
,当
时,有
这时,我们就说函数 在区间 上是这减函数.
函数单调性的概念:
一般地,设函数y=f(x)的定义域为I,如果对于定义域I内的某个区间D内的任意两个自变量x1,x2,当x11.增函数
知识要点
一般地,设函数y=f(x)的定义域为I,如果对于定义域I内的某个区间D内的任意两个自变量x1,x2 ,当x1f(x2) ,那么就说f(x)在区间D上是减函数 ,如图2.
y
x
0
x1
x2
f(x1)
f(x2)
y=f(x)
图1
y
x
0
x1
x2
f(x1)
f(x2)
y=f(x)
图2
1、函数的单调性是在定义域内的某个区间上的性质,是函数的局部性质.
2 、必须是对于区间D内的任意两个自变量x1,x2;当x1f(x2) 分别是增函数和减函数.
注意
在某区间上,
减函数
图象下降。
增函数
图象上升
x
y
o
x
y
o
如果函数y=f(x)在某个区间上是增函数或是减函数,那么就说函数y=f(x)在这一区间具有(严格的)单调性,区间D叫做y=f(x)的单调区间.
函数的单调性定义
例1 下图是定义在区间[-4,5]上的函数y=f (x),根据图像说出函数的单调区间,以及在每一单调区间上,它是增函数还是减函数?
1
2
3
4
5
-1
-2
-3
-4
-2
-3
2
3
o
解:函数y=f(x)的单调区间有[-4,-2),[-2,-1),[-1,1),[1,3),[3,5],其中y=f (x)在区间
[-4,-2), [-1,1), [3,5]上是增函数,在区间
[-2,-1), [1,3)上是减函数.
例2 物理学中的玻意耳定律 告诉我们,对于一定量的气体,当其体积V减小时,压强p将增大,试用函数单调性证明之.
分析:按题意就是证明函数 在区间 上是减函数.
证明:根据单调性的定义,设V1,V2是定义域(0,+∞)上的任意两个实数,且V1由V1,V2∈ (0,+∞)且V10, V2- V1 >0
又k>0,于是
所以,函数 是减函数.也就是说,当体积V减少时,压强p将增大.
取值
定号
作差变形
结论
用定义证明函数单调性的步骤是:
(1)取值
(2)作差变形
(3)定号
(4)判断
根据单调性的定义得结论
即取 是该区间内的任意两个值且
即求 ,通过因式分解、配方、有理化等方法
即根据给定的区间和 的符号的确定
的符号
例3 求证:函数 在区间 上是单调增函数.
,则
证明:在区间(0,+∞)上任取两个值 且
又因为 , ,所以说
即函数 在区间(0,+∞)上是单调增函数.
若把区间改为 ,结论变化吗
思考
自己动手做一下吧
若把函数改为
结论变化吗?
探究
画出反比例函数 的图象.
1 这个函数的定义域是什么?
2 它在定义域I上的单调性怎样?证明你的结论.
x
y
0
{x∣x≠0}
分两个区间(0,+∞), (- ∞ ,0)来考虑其单调性.
函数f(x)=1/x 在(0,+∞)上是减函数.
f(x1)- f(x2)=
由于x1,x2 得x1x2>0,又由x10
所以f(x1)- f(x2)>0, 即f(x1)> f(x2).
证明:(1)在区间(0,+∞)上,设x1,x2是(0,+∞)上任意两个实数,且x1(2)在区间(- ∞ ,0)上,同理可得到函数f(x)=1/x 在(- ∞ ,0)上是减函数。综上所述,函数f(x)=1/x 在定义域上是减函数.
下列两个函数的图象:
图1
o
x0
x
M
y
y
x
o
x0
图2
M
观 察
观察这两个函数图象,图中有个最高点,那么这个最高点的纵坐标叫什么呢?
思考
设函数y=f(x)图象上最高点的纵坐标为M,
则对函数定义域内任意自变量x,f(x)与M的大小
关系如何?
思考
f(x)< M
(0)=1
O
1
2
2、存在0,使得 (0)=1.
1、对任意的 都有 (x)≤1.
1是此函数的最大值
知识要点
M是函数y= f (x)的最大值(maximum value):
一般地,设函数y= f (x)的定义域为I,如果存在实数M满足:
(1)对于任意的x ∈I,都有f (x) ≤M;
(2)存在 ,使得 .
一般地,设函数y=f(x)的定义域为I,如果实数M满足:
(1)对于任意的的x∈I,都有f(x) ≥M;
(2)存在 ,使得 ,
那么我们称M是函数y=f(x)的最小值(minimun value).
能否仿照函数的最大值的定义,给出函数y=f(x)的最小值的定义呢?
思考
函数的最大值是函数值域中的一个元素吗?
思考
是
如果在函数f(x)定义域内存在x1和 x2,使对定义域内任意x都有 成立,由此你能得到什么结论?如果函数f(x)的最大值是b,最小值是a,那么函数f(x)的值域是[a,b]吗?
思考
函数f(x)在定义域中既有最大值又有最小值.
探究:函数单调性与函数的最值的关系
(1)若函数y=f (x)在区间[m,n] (mO
x
y
当x=m时,f (x)有最小值f (m),当x=n时,f (x)有最大值f (n).
(2)若函数y=f(x)在区间[m,n]上单调递减,则函数y=f(x)的最值是什么?
O
x
y
当x=m时,f (x)有最大值f (m),当x=n时,f(x)有最小值f (n).
(3)若函数 则函数y=f(x)在区间[m,n]上的最值是什么?
O
x
y
最大值f (l)=h,有最小值f (m), f (n)中较小者.
解:做出函数 的图像。显然,函数图像的顶点就是烟花上升的最高点,顶点的横坐标就是烟花爆裂的最佳时刻,纵坐标就是这时距地面的高度.
o
t
h
4
3
2
1
5
10
15
20
由二次函数的知识,对于函数
,我们有
当 时,函数有最大值
所以,烟花冲出1.5s是它爆裂的最佳时刻,此时距离地面的高度约为29m.
例5 已知函数 ,求函数的最大值与最小.
分析:由函数的图象可知道,此函数在[3,5]上递减。所以在区间[3,5]的两个端点上分别取得最大值与最小值.
解:设 是区间[3,5]上的任意两个实数,且 ,则
由于 得
于是
即
所以,此函数在区间[3,5]的两个端点上分别取得最大值与最小值即在x=3时取得最大值是1,在x=5时取得最小值为0.5.
课堂小结
2、函数单调性的定义;
3、证明函数单调性的步骤;
1、单调函数的图象特征;
4、函数的最值:
最大值
最小值
5、函数的最值的求法
(1)利用二次函数的性质(配方法)求函数的最值;
(2)利用图象求函数的最值;
(3)利用函数单调性求函数的最值 .
课堂练习
1.填表
函数
单调区间
k >0
k <0
k >0
k <0
增函数
减函数
减函数
增函数
单调性
函数
单调区间
单调性
增函数
增函数
减函数
减函数
最大
0.5
0.2
-2
5 . 设b>1为常数,如果当x∈[1,b]时,函数
的值域也是[1,b],求b的值.
x
y
0
1
1
解:因为
所以f(x)在x=1时取得最小值为1,又因为x∈[1,b],由f(x)的图像可知道在区间[1,b]上是递增的,所以
得b=3或b=-1,因为b>1,所以说b=3.
x
y
0
2
2
-2
-2
课题导入
函数是描述事物运动变化规律的数学模型,了解函数的变化规律势在必得。观察下面函数的图象,能说出它们的变化规律吗?
x
y
0
2
-2
2
-2
x
y
0
2
2
-2
-2
保持量(百分数)
天数
1 2 3 4 5 6
0
20
40
60
80
100
某市一天的温度变化图:
y=f(x),x∈[0,24]
说出气温在哪些时间段内是逐渐升高或下降的
问题1
画出f(x)=x的图像,并观察其图像。
2、在区间 ________上,随着x的增大,f(x)的值随着 ______.
o
5
-5
-5
5
f(x)=x
1、从左至右图象上升还是下降 ____
上升
增大
1、在区间 ________ 上,f(x)的值随着x的增大而 ______.
问题2
画出 的图像,并观察图像.
o
5
-5
-5
5
2、 在区间 ________ 上,f(x)的值随着x的增大而 _____.
(-∞,0]
(0,+∞)
减小
增大
对于二次函数 ,我们可以这样描述“在区间 上,随x的增大,相应的f(x)也随着增大”.
在区间 上,任取两个 ,得到
,当
时,有
这时,我们就说函数 在区间 上是这增函数.
x
y
2
1
0
1
3
(1)对于函数y= f(x) ,若在区间 I 上,当x=1时, y=1; 当 x=2时, y=3 , 能说在区间 I 上函数值 y 随自变量 x的增大而增大吗
思考
(2)对于函数y= f(x) ,若在区间 I 上,当x=1, 2, 3, 4, 时, 相应地 y=1, 3, 4, 5,能说在区间 I 上函数值y 随自变量x 的增大而增大吗?
思考
x
y
1
0
3
4
2
1
2
3
4
x
y
x1
0
x2
x3
xn
y1
y2
y3
yn
x应该取区间I内所有实数
(3) 对于函数y= f(x)若 区间I 上有n个数
x1< x2
若x取无数个呢
能否仿照前面的描述,说明函数
在区间(-∞,0]上是减函数吗?
在区间(-∞,0] 上,任取两个 ,得到
,当
时,有
这时,我们就说函数 在区间 上是这减函数.
函数单调性的概念:
一般地,设函数y=f(x)的定义域为I,如果对于定义域I内的某个区间D内的任意两个自变量x1,x2,当x1
知识要点
一般地,设函数y=f(x)的定义域为I,如果对于定义域I内的某个区间D内的任意两个自变量x1,x2 ,当x1
y
x
0
x1
x2
f(x1)
f(x2)
y=f(x)
图1
y
x
0
x1
x2
f(x1)
f(x2)
y=f(x)
图2
1、函数的单调性是在定义域内的某个区间上的性质,是函数的局部性质.
2 、必须是对于区间D内的任意两个自变量x1,x2;当x1
注意
在某区间上,
减函数
图象下降。
增函数
图象上升
x
y
o
x
y
o
如果函数y=f(x)在某个区间上是增函数或是减函数,那么就说函数y=f(x)在这一区间具有(严格的)单调性,区间D叫做y=f(x)的单调区间.
函数的单调性定义
例1 下图是定义在区间[-4,5]上的函数y=f (x),根据图像说出函数的单调区间,以及在每一单调区间上,它是增函数还是减函数?
1
2
3
4
5
-1
-2
-3
-4
-2
-3
2
3
o
解:函数y=f(x)的单调区间有[-4,-2),[-2,-1),[-1,1),[1,3),[3,5],其中y=f (x)在区间
[-4,-2), [-1,1), [3,5]上是增函数,在区间
[-2,-1), [1,3)上是减函数.
例2 物理学中的玻意耳定律 告诉我们,对于一定量的气体,当其体积V减小时,压强p将增大,试用函数单调性证明之.
分析:按题意就是证明函数 在区间 上是减函数.
证明:根据单调性的定义,设V1,V2是定义域(0,+∞)上的任意两个实数,且V1
又k>0,于是
所以,函数 是减函数.也就是说,当体积V减少时,压强p将增大.
取值
定号
作差变形
结论
用定义证明函数单调性的步骤是:
(1)取值
(2)作差变形
(3)定号
(4)判断
根据单调性的定义得结论
即取 是该区间内的任意两个值且
即求 ,通过因式分解、配方、有理化等方法
即根据给定的区间和 的符号的确定
的符号
例3 求证:函数 在区间 上是单调增函数.
,则
证明:在区间(0,+∞)上任取两个值 且
又因为 , ,所以说
即函数 在区间(0,+∞)上是单调增函数.
若把区间改为 ,结论变化吗
思考
自己动手做一下吧
若把函数改为
结论变化吗?
探究
画出反比例函数 的图象.
1 这个函数的定义域是什么?
2 它在定义域I上的单调性怎样?证明你的结论.
x
y
0
{x∣x≠0}
分两个区间(0,+∞), (- ∞ ,0)来考虑其单调性.
函数f(x)=1/x 在(0,+∞)上是减函数.
f(x1)- f(x2)=
由于x1,x2 得x1x2>0,又由x1
所以f(x1)- f(x2)>0, 即f(x1)> f(x2).
证明:(1)在区间(0,+∞)上,设x1,x2是(0,+∞)上任意两个实数,且x1
下列两个函数的图象:
图1
o
x0
x
M
y
y
x
o
x0
图2
M
观 察
观察这两个函数图象,图中有个最高点,那么这个最高点的纵坐标叫什么呢?
思考
设函数y=f(x)图象上最高点的纵坐标为M,
则对函数定义域内任意自变量x,f(x)与M的大小
关系如何?
思考
f(x)< M
(0)=1
O
1
2
2、存在0,使得 (0)=1.
1、对任意的 都有 (x)≤1.
1是此函数的最大值
知识要点
M是函数y= f (x)的最大值(maximum value):
一般地,设函数y= f (x)的定义域为I,如果存在实数M满足:
(1)对于任意的x ∈I,都有f (x) ≤M;
(2)存在 ,使得 .
一般地,设函数y=f(x)的定义域为I,如果实数M满足:
(1)对于任意的的x∈I,都有f(x) ≥M;
(2)存在 ,使得 ,
那么我们称M是函数y=f(x)的最小值(minimun value).
能否仿照函数的最大值的定义,给出函数y=f(x)的最小值的定义呢?
思考
函数的最大值是函数值域中的一个元素吗?
思考
是
如果在函数f(x)定义域内存在x1和 x2,使对定义域内任意x都有 成立,由此你能得到什么结论?如果函数f(x)的最大值是b,最小值是a,那么函数f(x)的值域是[a,b]吗?
思考
函数f(x)在定义域中既有最大值又有最小值.
探究:函数单调性与函数的最值的关系
(1)若函数y=f (x)在区间[m,n] (m
x
y
当x=m时,f (x)有最小值f (m),当x=n时,f (x)有最大值f (n).
(2)若函数y=f(x)在区间[m,n]上单调递减,则函数y=f(x)的最值是什么?
O
x
y
当x=m时,f (x)有最大值f (m),当x=n时,f(x)有最小值f (n).
(3)若函数 则函数y=f(x)在区间[m,n]上的最值是什么?
O
x
y
最大值f (l)=h,有最小值f (m), f (n)中较小者.
解:做出函数 的图像。显然,函数图像的顶点就是烟花上升的最高点,顶点的横坐标就是烟花爆裂的最佳时刻,纵坐标就是这时距地面的高度.
o
t
h
4
3
2
1
5
10
15
20
由二次函数的知识,对于函数
,我们有
当 时,函数有最大值
所以,烟花冲出1.5s是它爆裂的最佳时刻,此时距离地面的高度约为29m.
例5 已知函数 ,求函数的最大值与最小.
分析:由函数的图象可知道,此函数在[3,5]上递减。所以在区间[3,5]的两个端点上分别取得最大值与最小值.
解:设 是区间[3,5]上的任意两个实数,且 ,则
由于 得
于是
即
所以,此函数在区间[3,5]的两个端点上分别取得最大值与最小值即在x=3时取得最大值是1,在x=5时取得最小值为0.5.
课堂小结
2、函数单调性的定义;
3、证明函数单调性的步骤;
1、单调函数的图象特征;
4、函数的最值:
最大值
最小值
5、函数的最值的求法
(1)利用二次函数的性质(配方法)求函数的最值;
(2)利用图象求函数的最值;
(3)利用函数单调性求函数的最值 .
课堂练习
1.填表
函数
单调区间
k >0
k <0
k >0
k <0
增函数
减函数
减函数
增函数
单调性
函数
单调区间
单调性
增函数
增函数
减函数
减函数
最大
0.5
0.2
-2
5 . 设b>1为常数,如果当x∈[1,b]时,函数
的值域也是[1,b],求b的值.
x
y
0
1
1
解:因为
所以f(x)在x=1时取得最小值为1,又因为x∈[1,b],由f(x)的图像可知道在区间[1,b]上是递增的,所以
得b=3或b=-1,因为b>1,所以说b=3.
