2021-2022学年冀教版九年级数学上册第二十六章 解直角三角形单元测试题(word版含答案)
文档属性
| 名称 | 2021-2022学年冀教版九年级数学上册第二十六章 解直角三角形单元测试题(word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 320.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-06 18:13:19 | ||
图片预览




文档简介
第二十六章
解直角三角形
[时间:120分钟 分值:120分]
一、选择题(本大题有16个小题,1~10小题各3分;11~16小题,各2分,在每小题给出的四个选项中,只有一项是符合题目要求的)
1.在Rt△ABC中,若各边长度都扩大为原来的2倍,则锐角A的正弦值和正切值( )
A.都缩小为原来的
B.都扩大为原来的2倍
C.都没有变化
D.不能确定
2.在5×5的正方形网格中,∠AOB的位置如图1所示,则sin∠AOB的值为( )
图1
A.
B.
C.
D.2
3.在Rt△ABC中,已知∠C=90°,AC=3,BC=4,那么∠A的余弦值等于( )
A.
B.
C.
D.
4.计算8tan45°-4sin30°的结果是
( )
A.4
B.5
C.5
D.6
5.在Rt△ABC中,∠C=90°,若BC=1,AB=,则∠A的度数为
( )
A.30°
B.45°
C.50°
D.60°
6.如图2,在Rt△ABC中,CD是斜边AB上的中线,已知CD=5,AC=6,则tan∠DCB的值是( )
图2
A.
B.
C.
D.
7.在Rt△ABC中,∠ACB=90°,若AB=,tanB=2,则AC的长为( )
A.1
B.2
C.
D.2
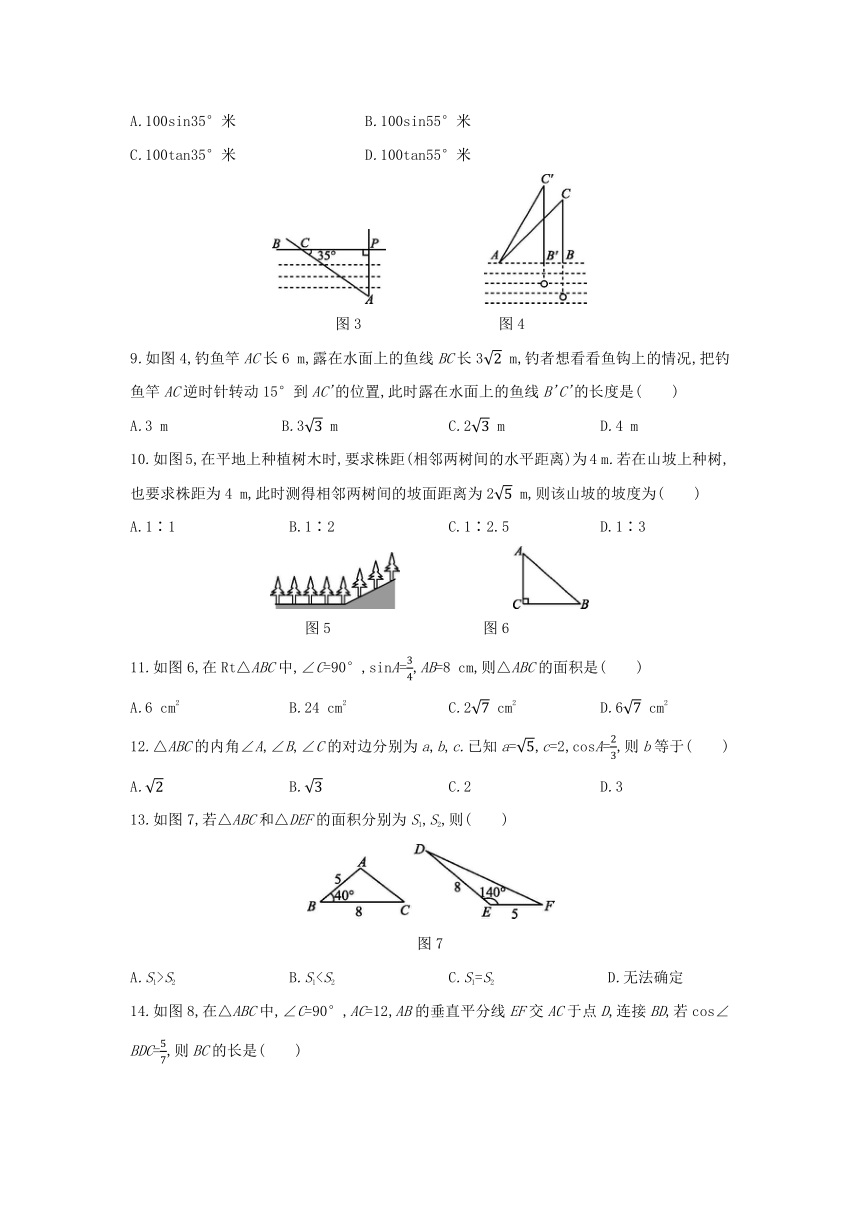
8.如图3,要测量小河两岸相对的两点P,A间的距离,可以在小河边取PA的垂线PB上的一点C,测得PC=100米,∠PCA=35°,则小河的宽PA为( )
A.100sin35°米
B.100sin55°米
C.100tan35°米
D.100tan55°米
图3
图4
9.如图4,钓鱼竿AC长6
m,露在水面上的鱼线BC长3
m,钓者想看看鱼钩上的情况,把钓鱼竿AC逆时针转动15°到AC'的位置,此时露在水面上的鱼线B'C'的长度是( )
A.3
m
B.3
m
C.2
m
D.4
m
10.如图5,在平地上种植树木时,要求株距(相邻两树间的水平距离)为4
m.若在山坡上种树,也要求株距为4
m,此时测得相邻两树间的坡面距离为2
m,则该山坡的坡度为( )
A.1∶1
B.1∶2
C.1∶2.5
D.1∶3
图5
图6
11.如图6,在Rt△ABC中,∠C=90°,sinA=,AB=8
cm,则△ABC的面积是( )
A.6
cm2
B.24
cm2
C.2
cm2
D.6
cm2
12.△ABC的内角∠A,∠B,∠C的对边分别为a,b,c.已知a=,c=2,cosA=,则b等于( )
A.
B.
C.2
D.3
13.如图7,若△ABC和△DEF的面积分别为S1,S2,则( )
图7
A.S1>S2
B.S1C.S1=S2
D.无法确定
14.如图8,在△ABC中,∠C=90°,AC=12,AB的垂直平分线EF交AC于点D,连接BD,若cos∠BDC=,则BC的长是( )
图8
A.10
B.8
C.4
D.2
15.如图9,考古队在A处测得古塔BC顶端C的仰角为45°,斜坡AD长10米,坡度i=3∶4,BD长12米,则古塔BC的高度为( )
A.25.5米
B.26米
C.28.5米
D.20.5米
图9
图10
16.如图10,一渔船在海岛A南偏东20°方向的B处遇险,测得海岛A与B的距离为20海里,渔船将险情报告给位于A处的救援船后,沿北偏西80°方向向海岛C靠近.同时,从A处出发的救援船沿南偏西10°方向匀速航行.20分钟后,救援船在海岛C处恰好与渔船相遇,那么救援船航行的速度为( )
A.10海里/时
B.30海里/时
C.20海里/时
D.30海里/时
二、填空题(本大题有3个小题,共11分.17小题3分,18~19小题各有2个空,每空2分,把答案写在题中横线上)
17.已知∠A是锐角,且满足3tanA-=0,则∠A= °.
18.如图11,小明为了测量小河对岸大树BC的高度,他在点A测得大树顶端B的仰角是45°,沿斜坡走2米到达斜坡上点D,在此处测得大树顶端点B的仰角为30°,且斜坡AF的坡比为1∶2.则小明从点A走到点D的过程中,他上升的高度为 米,大树BC的高度为 米(结果保留根号).
图11
19.如图12所示,把n个边长为1的正方形拼成一排,求得tan∠BA1C=1,tan∠BA2C=,
tan∠BA3C=,计算tan∠BA4C= ……按此规律写出tan∠BAnC= (用含n的代数式表示).
图12
三、解答题(本大题有7个小题,共67分,解答应写出文字说明,证明过程或演算步骤)
20.(本小题满分8分)如图13,P是∠α的边OA上的一点,已知点P的横坐标为6,若tanα=.
(1)求点P的纵坐标;
(2)求∠α的其他的三角函数值.
图13
21.(本小题满分9分)如图14,AD是△ABC的中线,tanB=,cosC=,AC=.
(1)求BC的长;
(2)求∠ADC的正弦值.
图14
22.(本小题满分9分)如图15,已知∠ABM=37°,AB=20,C是射线BM上一点.
(1)求点A到BM的距离.
(2)在下列条件中,可以唯一确定BC长的是 .(填写所有符合条件的序号)
①AC=13;②tan∠ACB=;③连接AC,△ABC的面积为126.
(3)在(2)的答案中,选择一个作为条件,画出草图,求BC的长.
(参考数据:sin37°≈0.6,cos37°≈0.8,tan37°≈0.75)
图15
23.(本小题满分9分)如图16,已知在Rt△ABC中,∠ACB=90°,CD是斜边AB上的中线,过点A作AE⊥CD,AE分别与CD,CB相交于点H,E,AH=2CH.
(1)求sinB的值;
(2)若CD=,求BE的长.
图16
24.(本小题满分10分)如图17,为测量一座山峰CF的高度,将此山的某侧山坡划分为AB和BC两段,每一段山坡近似是“直”的,测得坡长AB=800米,BC=200米,坡角∠BAF=30°,∠CBE=45°.
(1)求AB段山坡的高度EF;
(2)求山峰的高度CF.(≈1.414,结果精确到1米)
图17
25.(本小题满分10分)超速行驶是引发交通事故的主要原因.小明等三名同学运用自己所学的知识检测车速,他们将观测点设在距成纪大道100米的点C处,如图18所示,直线l表示成纪大道.一辆小汽车由成纪大道上的A处匀速行驶到B处,用时5秒.经测量,点A在点C的北偏西60°方向上,点B在点C的北偏西45°方向上.
(1)求A,B之间的距离(精确到0.1米);
(2)请判断此车是否超过了成纪大道60千米/时的限制速度.(参考数据:≈1.414,≈1.732)
图18
26.(本小题满分12分)如图19①是一种手机平板支架,由托板、支撑板和底座构成,手机放置在托板上,图②是其侧面结构示意图.量得托板长AB=120
mm,支撑板长CD=80
mm,底座长DE=90
mm.托板AB固定在支撑板顶端点C处,且CB=40
mm,托板AB可绕点C转动,支撑板CD可绕点D转动.(结果保留小数点后一位)
(1)若∠DCB=80°,∠CDE=60°,求点A到直线DE的距离;
(2)为了观看舒适,在(1)的情况下,把AB绕点C逆时针旋转10°后,再将CD绕点D顺时针旋转,使点B落在直线DE上即可,求CD旋转的角度.(参考数据:sin40°≈0.643,cos40°≈0.766,tan40°≈0.839,sin26.6°≈0.448,cos26.6°≈0.894,tan26.6°≈0.500,≈1.732)
图19
答案
1.C
2.B
3.A [解析]在Rt△ABC中,∵∠C=90°,AC=3,BC=4,∴AB==5,∴cosA=.
4.D [解析]8tan45°-4sin30°=8×1-4×=6.
5.B [解析]在Rt△ABC中,∵∠C=90°,∴∠A为锐角.∵sinA=,∴∠A=45°.
6.D [解析]由直角三角形的性质,得AB=2CD=2BD=10.由勾股定理,得BC=8,由等腰三角形的性质,得∠DCB=∠B,∴tan∠DCB=tanB=.
7.B [解析]在Rt△ABC中,∵∠ACB=90°,tanB=2,∴=2,∴BC=AC.由勾股定理,得AB2=AC2+BC2,即()2=AC2+(AC)2,解得AC=2.
8.C [解析]∵PA⊥PB,PC=100米,∠PCA=35°,∴小河宽PA=PC·tan∠PCA=100tan35°米.
9.B [解析]∵sin∠CAB=,∴∠CAB=45°.
∵∠C'AC=15°,∴∠C'AB'=60°,∴sin60°=,解得B'C'=3(m).故选B.
10.B [解析]如图,由勾股定理,得AC==2(m),
∴,即该山坡的坡度为1∶2.
11.D [解析]在Rt△ABC中,∵∠C=90°,AB=8cm,sinA=,∴BC=6cm,
∴AC==2(cm),∴S△ABC=BC·AC=×6×2=6(cm2).
12.D [解析]如图,过点B作BH⊥AC于点H.在Rt△ABH中,∵∠BHA=90°,∴cosA=,∴AH=,∴BH=.
在Rt△CBH中,CH=,∴AC=AH+CH==3.
13.C [解析]如图,过点A作AG⊥BC于点G,过点D作DH⊥EF交FE的延长线于点H.
在Rt△ABG中,AG=AB·sin40°=5sin40°.∵∠DEH=180°-140°=40°,∴在Rt△DHE中,DH=DE·sin40°=8sin40°,∴S1=×8×5sin40°=20sin40°,S2=×5×8sin40°=20sin40°,∴S1=S2.
14.D [解析]∵∠C=90°,cos∠BDC=,∴设CD=5x,则BD=7x,∴BC=2x.∵AB的垂直平分线EF交AC于点D,∴AD=BD=7x,∴AC=12x.∵AC=12,∴x=1,∴BC=2.
15.B [解析]如图,过点A作AE⊥BC于点E,AF⊥BD,交BD的延长线于点F,易知四边形AFBE是矩形,∴AF=BE,AE=BF.由i=3∶4,可设AF=3x米,DF=4x米.∵AD=10米,∴9x2+16x2=100,解得x=2(负值已舍去),则AF=BE=6米,DF=8米,∴AE=BF=DF+BD=8+12=20(米).∵∠CAE=45°,
∴CE=AE=20米,则BC=CE+BE=20+6=26(米).
16.D [解析]∵∠CAB=10°+20°=30°,∠CBA=80°-20°=60°,∴∠ACB=90°,
∴AC=AB·sin∠CBA=20×=10(海里),∴救援船航行的速度为10÷=30(海里/时).
17.30 [解析]∵3tanA-=0,∴tanA=,∴∠A=30°.
18.2 (3+5) [解析]如图,过点D作DK⊥BC于点K,DH⊥CE于点H,则四边形DHCK为矩形,故DK=CH,CK=DH.
在Rt△AHD中,∵,AD=2米,
∴DH=2米,AH=4米,∴CK=DH=2米,设BC=x米,在Rt△ABC中,∵∠BAC=45°,∴AC=BC=x米,
∴DK=CH=AH+AC=(4+x)米,BK=BC-CK=(x-2)米.在Rt△BDK中,∵BK=DK·tan30°,
∴x-2=(4+x)×,解得x=3+5,∴BC=(3+5)米,即大树的高度为(3+5)米.
19. [解析]如图,
过点C作CH⊥BA4于点H,由勾股定理,得BA4=,A4C=,△BA4C的面积=×1×1=,
∴×CH=,解得CH=,
则A4H=,
∴tan∠BA4C=.
1=12-1+1,3=22-2+1,7=32-3+1,
∴tan∠BAnC=.故答案为,.
20.解:(1)如图,过点P作PM⊥x轴于点M,则∠PMO=90°.
∵点P的横坐标为6,∴OM=6.
∵tanα=,∴PM=8,∴点P的纵坐标是8.
(2)在Rt△OMP中,
∵∠PMO=90°,PM=8,OM=6,
∴OP==10,
∴sinα=,cosα=.
21.解:(1)如图,过点A作AH⊥BC于点H.
在Rt△ACH中,
∵cosC=,AC=,∴CH=1,∴AH==1.
在Rt△ABH中,∵tanB=,∴BH=5,∴BC=BH+CH=6.
(2)∵BD=CD,∴CD=3,∴DH=2,
∴AD=.
在Rt△ADH中,sin∠ADH=,
∴∠ADC的正弦值为.
22.解:(1)如图,过点A作AD⊥BM于点D,则∠ADB=90°.
在Rt△ABD中,
∵∠ADB=90°,
∴AD=AB·sinB≈20×0.6=12.
即点A到BM的距离约为12.
(2)②③ [解析]①以点A为圆心、13为半径画圆,与BM有两个交点,不唯一;
②由tan∠ACB=知∠ACB的大小确定,在△ABC中,∠ACB,∠B及AB确定,此时的三角形唯一;③AB的长度和三角形的面积均确定,则点C到AB的距离即可确定,则BM上的点C是唯一的.
(3)(答案不唯一)方案一:选②,如图,由(1),得AD≈12,BD=AB·cosB≈16.
在Rt△ACD中,∵∠ADC=90°,∴CD=≈5,
∴BC=BD+CD≈21.
方案二:选③,如图,过点C作CE⊥AB于点E,则∠BEC=90°,由S△ABC=AB·CE=126,得CE=12.6.在Rt△BEC中,∵∠BEC=90°,
∴BC=≈21.
23.解:(1)∵△ABC是直角三角形,CD是斜边AB上的中线,
∴∠ACD+∠BCD=90°,CD=BD,
∴∠B=∠BCD.
∵AE⊥CD,
∴∠ACD+∠CAH=90°,∴∠B=∠CAH.
设CH=x,则AH=2x.
在Rt△ACH中,根据勾股定理,得AC=x,
∴sin∠CAH=,
∴sinB=.
(2)∵CD=,∴AB=2.
∵sinB=,
∴AC=2×=2,
∴BC==4.
∵sin∠CAH=,设CE=k,则AE=5k,
∴(k)2+22=(5k)2,
∴k=或k=-(舍去),
∴CE=1,则BE=BC-CE=3.
24.解:(1)过点B作BH⊥AF于点H,如图.
在Rt△ABH中,
∵sin∠BAH=,
∴BH=AB·sin∠BAH=800×sin30°=400(米),
∴EF=BH=400米.
答:AB段山坡的高度EF为400米.
(2)在Rt△CBE中,∵sin∠CBE=,
∴CE=BC·sin∠CBE=200×sin45°=100≈141.4(米),
∴CF=CE+EF≈141.4+400≈541(米).
答:山峰的高度CF约为541米.
25.解:(1)如图,过点C作CD⊥l于点D.根据题意可知CD=100米,∠ACD=60°,∠BCD=45°.
在Rt△ACD中,
∵tan∠ACD=,∴AD=100×tan60°=100≈173.20(米).
在Rt△BCD中,∵tan∠BCD=,
∴BD=100×tan45°=100(米),
∴AB=AD-BD≈173.20-100≈73.2(米).
答:A,B之间的距离约为73.2米.
(2)A,B之间的距离为73.2米,小汽车由A处行驶到B处,所用时间为5秒,可知其行驶速度为73.2÷5=14.64(米/秒)=52.704(千米/时).
∵52.704<60,∴该车没有超过成纪大道60千米/时的限制速度.
26.解:(1)如图①,过点A作AM⊥DE,交ED的延长线于点M,过点C作CF⊥AM,垂足为F,过点C作CN⊥DE,垂足为N.
由题意可知,AC=80,CD=80,∠DCB=80°,∠CDE=60°.
在Rt△CDN中,CN=CD·sin∠CDE=80×=40=FM,∠DCN=90°-60°=30°.
又∵∠DCB=80°,∴∠BCN=80°-30°=50°.
∵AM⊥DE,CN⊥DE,∴AM∥CN,∴∠A=∠BCN=50°,∴∠ACF=90°-50°=40°.
在Rt△AFC中,AF=AC·sin40°≈80×0.643=51.44,
∴AM=AF+FM≈51.44+40≈120.7(mm).
答:点A到直线DE的距离约为120.7mm.
(2)旋转后,如图②所示,根据题意可知∠DCB=80°+10°=90°.
在Rt△BCD中,CD=80mm,BC=40mm,∴tanD=≈0.500,∴∠D≈26.6°,
因此旋转的角度约为60°-26.6°=33.4°.
答:CD旋转的角度约为33.4°.
解直角三角形
[时间:120分钟 分值:120分]
一、选择题(本大题有16个小题,1~10小题各3分;11~16小题,各2分,在每小题给出的四个选项中,只有一项是符合题目要求的)
1.在Rt△ABC中,若各边长度都扩大为原来的2倍,则锐角A的正弦值和正切值( )
A.都缩小为原来的
B.都扩大为原来的2倍
C.都没有变化
D.不能确定
2.在5×5的正方形网格中,∠AOB的位置如图1所示,则sin∠AOB的值为( )
图1
A.
B.
C.
D.2
3.在Rt△ABC中,已知∠C=90°,AC=3,BC=4,那么∠A的余弦值等于( )
A.
B.
C.
D.
4.计算8tan45°-4sin30°的结果是
( )
A.4
B.5
C.5
D.6
5.在Rt△ABC中,∠C=90°,若BC=1,AB=,则∠A的度数为
( )
A.30°
B.45°
C.50°
D.60°
6.如图2,在Rt△ABC中,CD是斜边AB上的中线,已知CD=5,AC=6,则tan∠DCB的值是( )
图2
A.
B.
C.
D.
7.在Rt△ABC中,∠ACB=90°,若AB=,tanB=2,则AC的长为( )
A.1
B.2
C.
D.2
8.如图3,要测量小河两岸相对的两点P,A间的距离,可以在小河边取PA的垂线PB上的一点C,测得PC=100米,∠PCA=35°,则小河的宽PA为( )
A.100sin35°米
B.100sin55°米
C.100tan35°米
D.100tan55°米
图3
图4
9.如图4,钓鱼竿AC长6
m,露在水面上的鱼线BC长3
m,钓者想看看鱼钩上的情况,把钓鱼竿AC逆时针转动15°到AC'的位置,此时露在水面上的鱼线B'C'的长度是( )
A.3
m
B.3
m
C.2
m
D.4
m
10.如图5,在平地上种植树木时,要求株距(相邻两树间的水平距离)为4
m.若在山坡上种树,也要求株距为4
m,此时测得相邻两树间的坡面距离为2
m,则该山坡的坡度为( )
A.1∶1
B.1∶2
C.1∶2.5
D.1∶3
图5
图6
11.如图6,在Rt△ABC中,∠C=90°,sinA=,AB=8
cm,则△ABC的面积是( )
A.6
cm2
B.24
cm2
C.2
cm2
D.6
cm2
12.△ABC的内角∠A,∠B,∠C的对边分别为a,b,c.已知a=,c=2,cosA=,则b等于( )
A.
B.
C.2
D.3
13.如图7,若△ABC和△DEF的面积分别为S1,S2,则( )
图7
A.S1>S2
B.S1
D.无法确定
14.如图8,在△ABC中,∠C=90°,AC=12,AB的垂直平分线EF交AC于点D,连接BD,若cos∠BDC=,则BC的长是( )
图8
A.10
B.8
C.4
D.2
15.如图9,考古队在A处测得古塔BC顶端C的仰角为45°,斜坡AD长10米,坡度i=3∶4,BD长12米,则古塔BC的高度为( )
A.25.5米
B.26米
C.28.5米
D.20.5米
图9
图10
16.如图10,一渔船在海岛A南偏东20°方向的B处遇险,测得海岛A与B的距离为20海里,渔船将险情报告给位于A处的救援船后,沿北偏西80°方向向海岛C靠近.同时,从A处出发的救援船沿南偏西10°方向匀速航行.20分钟后,救援船在海岛C处恰好与渔船相遇,那么救援船航行的速度为( )
A.10海里/时
B.30海里/时
C.20海里/时
D.30海里/时
二、填空题(本大题有3个小题,共11分.17小题3分,18~19小题各有2个空,每空2分,把答案写在题中横线上)
17.已知∠A是锐角,且满足3tanA-=0,则∠A= °.
18.如图11,小明为了测量小河对岸大树BC的高度,他在点A测得大树顶端B的仰角是45°,沿斜坡走2米到达斜坡上点D,在此处测得大树顶端点B的仰角为30°,且斜坡AF的坡比为1∶2.则小明从点A走到点D的过程中,他上升的高度为 米,大树BC的高度为 米(结果保留根号).
图11
19.如图12所示,把n个边长为1的正方形拼成一排,求得tan∠BA1C=1,tan∠BA2C=,
tan∠BA3C=,计算tan∠BA4C= ……按此规律写出tan∠BAnC= (用含n的代数式表示).
图12
三、解答题(本大题有7个小题,共67分,解答应写出文字说明,证明过程或演算步骤)
20.(本小题满分8分)如图13,P是∠α的边OA上的一点,已知点P的横坐标为6,若tanα=.
(1)求点P的纵坐标;
(2)求∠α的其他的三角函数值.
图13
21.(本小题满分9分)如图14,AD是△ABC的中线,tanB=,cosC=,AC=.
(1)求BC的长;
(2)求∠ADC的正弦值.
图14
22.(本小题满分9分)如图15,已知∠ABM=37°,AB=20,C是射线BM上一点.
(1)求点A到BM的距离.
(2)在下列条件中,可以唯一确定BC长的是 .(填写所有符合条件的序号)
①AC=13;②tan∠ACB=;③连接AC,△ABC的面积为126.
(3)在(2)的答案中,选择一个作为条件,画出草图,求BC的长.
(参考数据:sin37°≈0.6,cos37°≈0.8,tan37°≈0.75)
图15
23.(本小题满分9分)如图16,已知在Rt△ABC中,∠ACB=90°,CD是斜边AB上的中线,过点A作AE⊥CD,AE分别与CD,CB相交于点H,E,AH=2CH.
(1)求sinB的值;
(2)若CD=,求BE的长.
图16
24.(本小题满分10分)如图17,为测量一座山峰CF的高度,将此山的某侧山坡划分为AB和BC两段,每一段山坡近似是“直”的,测得坡长AB=800米,BC=200米,坡角∠BAF=30°,∠CBE=45°.
(1)求AB段山坡的高度EF;
(2)求山峰的高度CF.(≈1.414,结果精确到1米)
图17
25.(本小题满分10分)超速行驶是引发交通事故的主要原因.小明等三名同学运用自己所学的知识检测车速,他们将观测点设在距成纪大道100米的点C处,如图18所示,直线l表示成纪大道.一辆小汽车由成纪大道上的A处匀速行驶到B处,用时5秒.经测量,点A在点C的北偏西60°方向上,点B在点C的北偏西45°方向上.
(1)求A,B之间的距离(精确到0.1米);
(2)请判断此车是否超过了成纪大道60千米/时的限制速度.(参考数据:≈1.414,≈1.732)
图18
26.(本小题满分12分)如图19①是一种手机平板支架,由托板、支撑板和底座构成,手机放置在托板上,图②是其侧面结构示意图.量得托板长AB=120
mm,支撑板长CD=80
mm,底座长DE=90
mm.托板AB固定在支撑板顶端点C处,且CB=40
mm,托板AB可绕点C转动,支撑板CD可绕点D转动.(结果保留小数点后一位)
(1)若∠DCB=80°,∠CDE=60°,求点A到直线DE的距离;
(2)为了观看舒适,在(1)的情况下,把AB绕点C逆时针旋转10°后,再将CD绕点D顺时针旋转,使点B落在直线DE上即可,求CD旋转的角度.(参考数据:sin40°≈0.643,cos40°≈0.766,tan40°≈0.839,sin26.6°≈0.448,cos26.6°≈0.894,tan26.6°≈0.500,≈1.732)
图19
答案
1.C
2.B
3.A [解析]在Rt△ABC中,∵∠C=90°,AC=3,BC=4,∴AB==5,∴cosA=.
4.D [解析]8tan45°-4sin30°=8×1-4×=6.
5.B [解析]在Rt△ABC中,∵∠C=90°,∴∠A为锐角.∵sinA=,∴∠A=45°.
6.D [解析]由直角三角形的性质,得AB=2CD=2BD=10.由勾股定理,得BC=8,由等腰三角形的性质,得∠DCB=∠B,∴tan∠DCB=tanB=.
7.B [解析]在Rt△ABC中,∵∠ACB=90°,tanB=2,∴=2,∴BC=AC.由勾股定理,得AB2=AC2+BC2,即()2=AC2+(AC)2,解得AC=2.
8.C [解析]∵PA⊥PB,PC=100米,∠PCA=35°,∴小河宽PA=PC·tan∠PCA=100tan35°米.
9.B [解析]∵sin∠CAB=,∴∠CAB=45°.
∵∠C'AC=15°,∴∠C'AB'=60°,∴sin60°=,解得B'C'=3(m).故选B.
10.B [解析]如图,由勾股定理,得AC==2(m),
∴,即该山坡的坡度为1∶2.
11.D [解析]在Rt△ABC中,∵∠C=90°,AB=8cm,sinA=,∴BC=6cm,
∴AC==2(cm),∴S△ABC=BC·AC=×6×2=6(cm2).
12.D [解析]如图,过点B作BH⊥AC于点H.在Rt△ABH中,∵∠BHA=90°,∴cosA=,∴AH=,∴BH=.
在Rt△CBH中,CH=,∴AC=AH+CH==3.
13.C [解析]如图,过点A作AG⊥BC于点G,过点D作DH⊥EF交FE的延长线于点H.
在Rt△ABG中,AG=AB·sin40°=5sin40°.∵∠DEH=180°-140°=40°,∴在Rt△DHE中,DH=DE·sin40°=8sin40°,∴S1=×8×5sin40°=20sin40°,S2=×5×8sin40°=20sin40°,∴S1=S2.
14.D [解析]∵∠C=90°,cos∠BDC=,∴设CD=5x,则BD=7x,∴BC=2x.∵AB的垂直平分线EF交AC于点D,∴AD=BD=7x,∴AC=12x.∵AC=12,∴x=1,∴BC=2.
15.B [解析]如图,过点A作AE⊥BC于点E,AF⊥BD,交BD的延长线于点F,易知四边形AFBE是矩形,∴AF=BE,AE=BF.由i=3∶4,可设AF=3x米,DF=4x米.∵AD=10米,∴9x2+16x2=100,解得x=2(负值已舍去),则AF=BE=6米,DF=8米,∴AE=BF=DF+BD=8+12=20(米).∵∠CAE=45°,
∴CE=AE=20米,则BC=CE+BE=20+6=26(米).
16.D [解析]∵∠CAB=10°+20°=30°,∠CBA=80°-20°=60°,∴∠ACB=90°,
∴AC=AB·sin∠CBA=20×=10(海里),∴救援船航行的速度为10÷=30(海里/时).
17.30 [解析]∵3tanA-=0,∴tanA=,∴∠A=30°.
18.2 (3+5) [解析]如图,过点D作DK⊥BC于点K,DH⊥CE于点H,则四边形DHCK为矩形,故DK=CH,CK=DH.
在Rt△AHD中,∵,AD=2米,
∴DH=2米,AH=4米,∴CK=DH=2米,设BC=x米,在Rt△ABC中,∵∠BAC=45°,∴AC=BC=x米,
∴DK=CH=AH+AC=(4+x)米,BK=BC-CK=(x-2)米.在Rt△BDK中,∵BK=DK·tan30°,
∴x-2=(4+x)×,解得x=3+5,∴BC=(3+5)米,即大树的高度为(3+5)米.
19. [解析]如图,
过点C作CH⊥BA4于点H,由勾股定理,得BA4=,A4C=,△BA4C的面积=×1×1=,
∴×CH=,解得CH=,
则A4H=,
∴tan∠BA4C=.
1=12-1+1,3=22-2+1,7=32-3+1,
∴tan∠BAnC=.故答案为,.
20.解:(1)如图,过点P作PM⊥x轴于点M,则∠PMO=90°.
∵点P的横坐标为6,∴OM=6.
∵tanα=,∴PM=8,∴点P的纵坐标是8.
(2)在Rt△OMP中,
∵∠PMO=90°,PM=8,OM=6,
∴OP==10,
∴sinα=,cosα=.
21.解:(1)如图,过点A作AH⊥BC于点H.
在Rt△ACH中,
∵cosC=,AC=,∴CH=1,∴AH==1.
在Rt△ABH中,∵tanB=,∴BH=5,∴BC=BH+CH=6.
(2)∵BD=CD,∴CD=3,∴DH=2,
∴AD=.
在Rt△ADH中,sin∠ADH=,
∴∠ADC的正弦值为.
22.解:(1)如图,过点A作AD⊥BM于点D,则∠ADB=90°.
在Rt△ABD中,
∵∠ADB=90°,
∴AD=AB·sinB≈20×0.6=12.
即点A到BM的距离约为12.
(2)②③ [解析]①以点A为圆心、13为半径画圆,与BM有两个交点,不唯一;
②由tan∠ACB=知∠ACB的大小确定,在△ABC中,∠ACB,∠B及AB确定,此时的三角形唯一;③AB的长度和三角形的面积均确定,则点C到AB的距离即可确定,则BM上的点C是唯一的.
(3)(答案不唯一)方案一:选②,如图,由(1),得AD≈12,BD=AB·cosB≈16.
在Rt△ACD中,∵∠ADC=90°,∴CD=≈5,
∴BC=BD+CD≈21.
方案二:选③,如图,过点C作CE⊥AB于点E,则∠BEC=90°,由S△ABC=AB·CE=126,得CE=12.6.在Rt△BEC中,∵∠BEC=90°,
∴BC=≈21.
23.解:(1)∵△ABC是直角三角形,CD是斜边AB上的中线,
∴∠ACD+∠BCD=90°,CD=BD,
∴∠B=∠BCD.
∵AE⊥CD,
∴∠ACD+∠CAH=90°,∴∠B=∠CAH.
设CH=x,则AH=2x.
在Rt△ACH中,根据勾股定理,得AC=x,
∴sin∠CAH=,
∴sinB=.
(2)∵CD=,∴AB=2.
∵sinB=,
∴AC=2×=2,
∴BC==4.
∵sin∠CAH=,设CE=k,则AE=5k,
∴(k)2+22=(5k)2,
∴k=或k=-(舍去),
∴CE=1,则BE=BC-CE=3.
24.解:(1)过点B作BH⊥AF于点H,如图.
在Rt△ABH中,
∵sin∠BAH=,
∴BH=AB·sin∠BAH=800×sin30°=400(米),
∴EF=BH=400米.
答:AB段山坡的高度EF为400米.
(2)在Rt△CBE中,∵sin∠CBE=,
∴CE=BC·sin∠CBE=200×sin45°=100≈141.4(米),
∴CF=CE+EF≈141.4+400≈541(米).
答:山峰的高度CF约为541米.
25.解:(1)如图,过点C作CD⊥l于点D.根据题意可知CD=100米,∠ACD=60°,∠BCD=45°.
在Rt△ACD中,
∵tan∠ACD=,∴AD=100×tan60°=100≈173.20(米).
在Rt△BCD中,∵tan∠BCD=,
∴BD=100×tan45°=100(米),
∴AB=AD-BD≈173.20-100≈73.2(米).
答:A,B之间的距离约为73.2米.
(2)A,B之间的距离为73.2米,小汽车由A处行驶到B处,所用时间为5秒,可知其行驶速度为73.2÷5=14.64(米/秒)=52.704(千米/时).
∵52.704<60,∴该车没有超过成纪大道60千米/时的限制速度.
26.解:(1)如图①,过点A作AM⊥DE,交ED的延长线于点M,过点C作CF⊥AM,垂足为F,过点C作CN⊥DE,垂足为N.
由题意可知,AC=80,CD=80,∠DCB=80°,∠CDE=60°.
在Rt△CDN中,CN=CD·sin∠CDE=80×=40=FM,∠DCN=90°-60°=30°.
又∵∠DCB=80°,∴∠BCN=80°-30°=50°.
∵AM⊥DE,CN⊥DE,∴AM∥CN,∴∠A=∠BCN=50°,∴∠ACF=90°-50°=40°.
在Rt△AFC中,AF=AC·sin40°≈80×0.643=51.44,
∴AM=AF+FM≈51.44+40≈120.7(mm).
答:点A到直线DE的距离约为120.7mm.
(2)旋转后,如图②所示,根据题意可知∠DCB=80°+10°=90°.
在Rt△BCD中,CD=80mm,BC=40mm,∴tanD=≈0.500,∴∠D≈26.6°,
因此旋转的角度约为60°-26.6°=33.4°.
答:CD旋转的角度约为33.4°.
同课章节目录
- 第23章 数据分析
- 23.1 平均数与加权平均数
- 23.2 中位数与众数
- 23.3 方差
- 23.4 用样本估计总体
- 第24章 一元二次方程
- 24.1 一元二次方程
- 24.2 解一元二次方程
- 24.3 一元二次方程根与系数的关系
- 24.4 一元二次方程的应用
- 第25章 图形的相似
- 25.1 比例线段
- 25.2 平行线分线段成比例
- 25.3 相似三角形
- 25.4 相似三角形的判定
- 25.5 相似三角形的性质
- 25.6 相似三角形的应用
- 25.7 相似多边形和图形的位似
- 第26章 解直角三角形
- 26.1 锐角三角函数
- 26.2 锐角三角函数的计算
- 26.3 解直角三角形
- 26.4 解直角三角形的应用
- 第27章 反比例函数
- 27.1 反比例函数
- 27.2 反比例函数的图像和性质
- 27.3 反比例函数的应用
- 第28章 圆
- 28.1 圆的概念和性质
- 28.2 过三点的圆
- 28.3 圆心角和圆周角
- 28.4 垂径定理
- 28.5 弧长和扇形面积
