2021-2022学年高一上学期数学人教A版必修1 2.1.2指数函数及其性质课件(共18张PPT)
文档属性
| 名称 | 2021-2022学年高一上学期数学人教A版必修1 2.1.2指数函数及其性质课件(共18张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-09 15:51:04 | ||
图片预览





文档简介
(共18张PPT)
2.1.2指数函数及其性质
情境引入
1.将一张作业本纸连续对折,折叠的次数x与对应的层数y之间存在着怎样的关系?
2.假设原面积为1,对折后的面积S与对折次数有怎样的关系?
实践并思考:
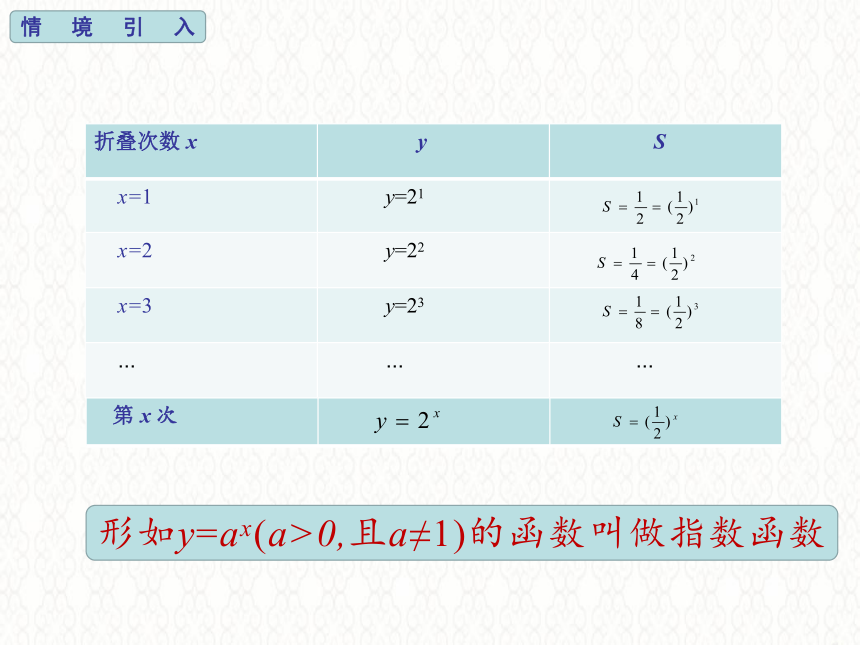
情境引入
折叠次数
x
y
S
x=1
y=21
x=2
y=22
x=3
y=23
...
...
...
第
x
次
形如y=ax(a>0,且a≠1)的函数叫做指数函数
指数函数的概念
指数函数的概念:
一般地,形如y=ax(a>0,且a≠1)的函数叫做指数函数,其中指数x是自变量,定义域为R.
解析式特点:
【1】ax的系数为1;
【2】ax的指数为自变量;
【3】ax的底数是大于零且不等于1的常数.
思考:为什么规定a>0,且a≠1?
类比初中学习函数,研究函数的一般方法:
背景
概念
图像与性质
应用
为了研究指数函数,首先作出指数函数的图像,然后借助指数函数的图像研究指数函数的性质.
指数函数的图象及其性质
回顾:初中学习画函数图象的基本步骤是什么?
列表
描点
连线
x
y
-2
-1.5
0.35
-1
-0.5
0.71
0
0.5
1.41
1
1.5
2.83
2
0.25
0.5
1
2
4
1
x
y
o
1
2
3
-1
-2
-3
请同学们完成x,y的对应值表,并用描点法画出函数
的图象.
指数函数的图象及其性质
x
y
-2
0.25
-1.5
0.35
-1
0.5
-0.5
0.71
0
1
0.5
1.41
1
2
1.5
2.83
2
4
x
y
-2
-1.5
2.83
-1
-0.5
1.41
0
0.5
0.71
1
1.5
0.35
2
4
2
1
0.5
0.25
指数函数的图象及其性质
1
x
y
o
1
2
3
-1
-2
-3
指数函数的图象及其性质
你能否用同样的方法作出
的图象呢?
1
x
y
o
1
2
3
-1
-2
-3
指数函数的图象及其性质
你能猜测出
的图象吗?
选取a的特殊值画图,猜测指数函数的图象按底数的取值,可分为01两种类型.
因此,指数函数的性质也可以分01两种情况进行
研究.
y=2x
y=3x
y=4x
指数函数的图象及其性质
选取底数a
(a>0且a≠1)的若干个不同的值,在同一直角坐标系内画出相应的指数函数的图象.观察这些图象的位置、公共点和变化趋势,它们有哪些共性?由此你能概括出指数函数y=ax
(a>0且a≠1)的值域和性质吗?
指数函数的图象及其性质
几何画板展示任意实数a
(a>0且a≠1)其图象变化.
a>1
0图像
定义域
值
域
过定点
性质
单调性
取
值
分
布
奇偶性
x
y
o
1
x
y
o
1
R
(0,+∞)
(0,1)
在R上是增函数
在R上是减函数
当x<0时,00时,y>1.
当x<0时,y>1;当x>0时,0既不是奇函数也不是偶函数
指数函数y=ax的图象和性质
指数函数的图象及其性质
指数函数的图象及其性质
记忆口诀
左右无限冲破天;
下与横轴永不连;
大一递增小一减;
定点(0,1)永不变。
例1:右图是指数函数:
①
y=ax,②
y=bx,
③y=cx,
④
y=d
x
的图象,
则a,b,c,d与1的大小关系是
(
)
A.aB.bC.1D.a【解析】画出直线x=1与四个指数函数的交点从下往上依次为(1,b),(1,a),(1,d),(1,c),所以有0.
故选:B.
函数y=ax在y轴右侧的图像,底数越大,图象越高(底大图高).
典例精讲
例2:若点
在指数函数
的图象上,求
的值.
例3:函数y=ax+1
(a>0且a≠1)的图像必过定点:
.
解:令x+1=0,得x
=-1,
所以当x=-1时,y=1,
所以y=ax+1(a>0且a≠1)的图像必过定点(-1,0).
作业布置:
聚焦课堂当堂反馈
谢谢各位老师指导!
2.1.2指数函数及其性质
情境引入
1.将一张作业本纸连续对折,折叠的次数x与对应的层数y之间存在着怎样的关系?
2.假设原面积为1,对折后的面积S与对折次数有怎样的关系?
实践并思考:
情境引入
折叠次数
x
y
S
x=1
y=21
x=2
y=22
x=3
y=23
...
...
...
第
x
次
形如y=ax(a>0,且a≠1)的函数叫做指数函数
指数函数的概念
指数函数的概念:
一般地,形如y=ax(a>0,且a≠1)的函数叫做指数函数,其中指数x是自变量,定义域为R.
解析式特点:
【1】ax的系数为1;
【2】ax的指数为自变量;
【3】ax的底数是大于零且不等于1的常数.
思考:为什么规定a>0,且a≠1?
类比初中学习函数,研究函数的一般方法:
背景
概念
图像与性质
应用
为了研究指数函数,首先作出指数函数的图像,然后借助指数函数的图像研究指数函数的性质.
指数函数的图象及其性质
回顾:初中学习画函数图象的基本步骤是什么?
列表
描点
连线
x
y
-2
-1.5
0.35
-1
-0.5
0.71
0
0.5
1.41
1
1.5
2.83
2
0.25
0.5
1
2
4
1
x
y
o
1
2
3
-1
-2
-3
请同学们完成x,y的对应值表,并用描点法画出函数
的图象.
指数函数的图象及其性质
x
y
-2
0.25
-1.5
0.35
-1
0.5
-0.5
0.71
0
1
0.5
1.41
1
2
1.5
2.83
2
4
x
y
-2
-1.5
2.83
-1
-0.5
1.41
0
0.5
0.71
1
1.5
0.35
2
4
2
1
0.5
0.25
指数函数的图象及其性质
1
x
y
o
1
2
3
-1
-2
-3
指数函数的图象及其性质
你能否用同样的方法作出
的图象呢?
1
x
y
o
1
2
3
-1
-2
-3
指数函数的图象及其性质
你能猜测出
的图象吗?
选取a的特殊值画图,猜测指数函数的图象按底数的取值,可分为0
因此,指数函数的性质也可以分0
研究.
y=2x
y=3x
y=4x
指数函数的图象及其性质
选取底数a
(a>0且a≠1)的若干个不同的值,在同一直角坐标系内画出相应的指数函数的图象.观察这些图象的位置、公共点和变化趋势,它们有哪些共性?由此你能概括出指数函数y=ax
(a>0且a≠1)的值域和性质吗?
指数函数的图象及其性质
几何画板展示任意实数a
(a>0且a≠1)其图象变化.
a>1
0
定义域
值
域
过定点
性质
单调性
取
值
分
布
奇偶性
x
y
o
1
x
y
o
1
R
(0,+∞)
(0,1)
在R上是增函数
在R上是减函数
当x<0时,0
当x<0时,y>1;当x>0时,0
指数函数y=ax的图象和性质
指数函数的图象及其性质
指数函数的图象及其性质
记忆口诀
左右无限冲破天;
下与横轴永不连;
大一递增小一减;
定点(0,1)永不变。
例1:右图是指数函数:
①
y=ax,②
y=bx,
③y=cx,
④
y=d
x
的图象,
则a,b,c,d与1的大小关系是
(
)
A.a
故选:B.
函数y=ax在y轴右侧的图像,底数越大,图象越高(底大图高).
典例精讲
例2:若点
在指数函数
的图象上,求
的值.
例3:函数y=ax+1
(a>0且a≠1)的图像必过定点:
.
解:令x+1=0,得x
=-1,
所以当x=-1时,y=1,
所以y=ax+1(a>0且a≠1)的图像必过定点(-1,0).
作业布置:
聚焦课堂当堂反馈
谢谢各位老师指导!
